基于改進Valiantzas方程的黃河下游柳園口灌區ET0預測研究

景 明，王軍濤，程獻國，高子樂

(1.黃河水利委員會黃河水利科學研究院， 河南 鄭州 450003； 2.黃河流域農村水利研究中心， 河南 新鄉 453003； 3.河南省豫東水利工程管理局惠北水利科學試驗站， 河南 開封 475000)

根據2006年國務院第472號令《黃河水量調度條例》，黃河水資源實行年度水量調度計劃與月、旬水量調度方案以及實時調度指令相結合的管理方式對干流用水過程進行統一調度，其中用水高峰時制訂并下達旬水量調度方案。旬調度方案需要對未來10 d左右各省(區)引黃需水量作出預測，重點是確定干流各省(區)灌溉需水量，需要對不同區域灌區的引黃灌溉過程作出預測。特別是2008年黃河水利委員會提出黃河功能性不斷流[1]以來，對農業灌溉用水過程的準確判斷成為黃河水量旬調度方案編制的關鍵技術問題。作為預測農業灌溉需水的重要參數，參考作物需水量(Evapotranspiration,ET0)的預測精度在很大程度上決定了灌溉預報的準確性和有效性[2-4]。目前計算ET0的常用方法是聯合國糧農組織(Food and Agriculture Organization of the United Nations, FAO)推薦的Penman-Monteith方法(簡稱P-M方法)[5]，但該方法輸入參數較多，且部分參數不能通過天氣預報等方式實現量化預報，導致P-M方法的預測ET0功能較差。國內外學者對ET0計算和預測方法開展了大量研究[6-14]，其中應用較為廣泛的是逐日均值修正模型[2]。2006年，Valiantzas研究建立了以特征氣溫和空氣相對濕度為基本輸入的ET0計算方法，即Valiantzas方程。該方程已在歐洲、非洲和印度等地得到了成功應用[8,15]。徐冬梅等[16]采用該方法研究了華北地區參考作物需水量變化。潘云等[17]首次將該方程引入中國并進行了修訂，認為采用修訂后的Valiantzas方法計算精度高于Priestley-Taylor模型[19]和Hargreaves模型[20]，在風速、日照時數缺乏情況下應用該方法計算ET0結果較好，其計算ET0的精度適合中國大部分地區。但潘云修訂后的Valiantzas方法仍需空氣相對濕度(Relative air humidity,RH)作為基本輸入參數，而RH目前尚不能實現量化預報，因此，本文研究建立了RH預測方法，進一步減少了Valiantzas方程輸入項的數量，并以黃河下游柳園口灌區為典型對Valiantzas方法進行了改進，增強其對ET0的預測功能，為黃河下游地區引黃灌溉需水量預報提供參考，同時為黃河水量旬調度方案編制提供技術支撐，推進黃河水量精細調度。

1 材料與方法

1.1 研究區概況

河南、山東兩省歷來是黃河水量調度的重要區域，灌區主要分布在黃河下游沖積平原。黃河下游引黃灌區屬暖溫帶半濕潤季風氣候，年均降水量510～790 mm，多年平均蒸發量1100～1 400 mm，冬春季雨雪稀少。灌區土壤主要有砂土、砂壤土、壤土和黏土。本文選取河南省境內的柳園口灌區為典型灌區。灌區位于河南省開封市，處在東經114°21′～114°27′，北緯34°35′～34°53′，在惠濟河以北，黃河大堤以南，東界三義寨引黃灌區，西連黑崗口灌區。灌區土壤主要有砂壤土、輕壤土，多年平均降水量627 mm，多年平均蒸發量1 316 mm。柳園口灌區在黃河下游引黃灌區中段，其土壤特性、氣候條件等與黃河下游引黃灌區具有較好的一致性，且黃河水是該灌區唯一的地表水灌溉水源，其氣候特征、水資源條件、農業種植模式等在黃河下游眾多引黃灌區中具有一定的代表性。

1.2 ET0計算方法

本文計算ET0的氣象數據選用位于柳園口灌區的河南省豫東水利工程管理局惠北水利科學試驗站氣象觀測場1993—2011年的逐日氣象資料，包括太陽輻射、日照時數、氣溫、風速、空氣相對濕度等參數。其中，采用1993—2010年數據建立相關模型，以2011年的相關數據驗證模型精度。

1.2.1 Penman-Monteith方法簡介 目前計算ET0的常用方法是FAO推薦的基于能量平衡和空氣動力學原理的Penman-Monteith方法，其計算方程為：

(1)

式中，ET0為參考作物騰發量(mm·d-1)；Δ為飽和水汽壓與溫度關系曲線的斜率；Rn為太陽輻射(MJ·m-2·day-1)；G為土壤熱通量(MJ·m-2·day-1)；γ為濕度計常數(kPa·℃-1)；T為空氣溫度(℃)；u2為在地面以上2 m高處的風速(m·s-1)；es為日平均飽和水汽壓(kPa)；ea為實際水汽壓(kPa)。

本文采用FAO推薦的ET0CalculatorV31計算了柳園口灌區逐年逐日ET0值。其中，對于氣象站沒有監測的項目，根據文獻[5]的方法，采用氣溫、空氣相對濕度、日照時數等常規觀測資料進行推求確定。

1.2.2 Valiantzas方法簡介 根據FAO推薦方法計算參考作物需水量輸入的參數較多，且空氣相對濕度、風速、日照時數等參數目前尚未實現實時量化預報，影響到參考作物需水量的中短期預報精度，與當前黃河水量旬調度方案編制的基礎數據預報時段要求不一致。因此，基于常規氣象預報數據的參考作物需水量計算方法，可以為土壤墑情預測、引黃灌區農業灌溉預報等提供有效的技術方法。2006年，Valiantzas等[17]根據能量平衡理論，對Penman-Monteith方法進行了簡化處理，建立了潛在水面蒸發的計算方程，即：

Epen=Erads-EradL+Eaero

(2)

式中，Epen為潛在水面蒸發量(mm)；Erad為入射短波輻射(mm)；EradL為向外長波輻射(mm)；Eaero為空氣動力部分(mm)。

在此基礎上，Valiantzas通過設定平均風速和水面反射率，建立了無風速數據輸入的水面潛在蒸發量計算公式：

(3)

式中，EPEN為水面潛在蒸發(mm)；Rs為太陽輻射(MJ·m-2·d-1)；T為平均氣溫(℃)；RA為大氣層外太陽輻射(MJ·m-2·d-1)，根據Hargreaves能量方程[20]，它主要與日地距離、太陽赤緯、日沒時角、日出時角等參數有關，可通過地理緯度、太陽赤緯角和日序數通過理論計算確定[21]；RH為空氣相對濕度(%)。

潘云等[17]通過修訂地表發射率等方法，對Valiantzas方法進行了修訂，建立了計算參考作物需水量的Valiantzas修訂方法：

(4)

式中，KRs為調節系數，FAO建議取值為0.16～0.19，根據潘云等人的研究，取0.17；Tmax和Tmin為日最高和最低氣溫(℃)；Δ為飽和水汽壓與溫度關系曲線的斜率，計算方法詳見參考文獻[6]。

從中國氣象數據網、歐洲中期天氣預報中心等氣象數據平臺獲悉，目前氣象數值預報尚不能提供未來10 d的空氣相對濕度(RH)預報值。因此，為提高Valiantzas方程的預測功能，本文在研究建立RH預測方法的基礎上，進一步改進Valiantzas方程，以適應黃河水量調度對灌區需水信息研判的實際需求。

1.2.3 改進Valiantzas方法

(1) 基于常規氣象預報數據的RH預測方法

通過分析，筆者首先建立了關于最高氣溫和最低氣溫的特征氣溫函數表達式：

W(Tmax，Tmin)=exp(Tmax-Tmin)0.21

(5)

式中，W(Tmax，Tmin)為逐日最高氣溫和最低氣溫的函數。

此外，研究建立了空氣相對濕度函數表達式：

G(RH)=(273.3+RH)/(Tmax-Tmin)

(6)

式中，G(RH)空氣相對濕度函數。

依據式(5)和式(6)，以柳園口灌區1993—2010年觀測的逐日RH,Tmax，Tmin為輸入，分別計算W(T)和G(RH)，尋求二者規律建立關系，推算RH估算式RH=f(Tmax，Tmin)。

(2) Valiantzas方法改進

通過對式(4)的研究認為，該表達式右部可分解為三項，其中KRs可視為常數項。因此，式(4)可表示為：

(7)

式中，a、b、c為待定系數，其它符號意義同前。

以Penman-Monteith方法計算的柳園口灌區ET0多年逐日平均值為因變量，對上式進行多元回歸分析，確定待定系數。

2 結果與分析

2.1 空氣相對濕度預測

根據上述方法，采用典型灌區1993—2010年逐日最高氣溫、最低氣溫和空氣相對濕度，分別計算式(5)和式(6)，建立特征氣溫函數與空氣相對濕度函數之間的關系，見圖1。

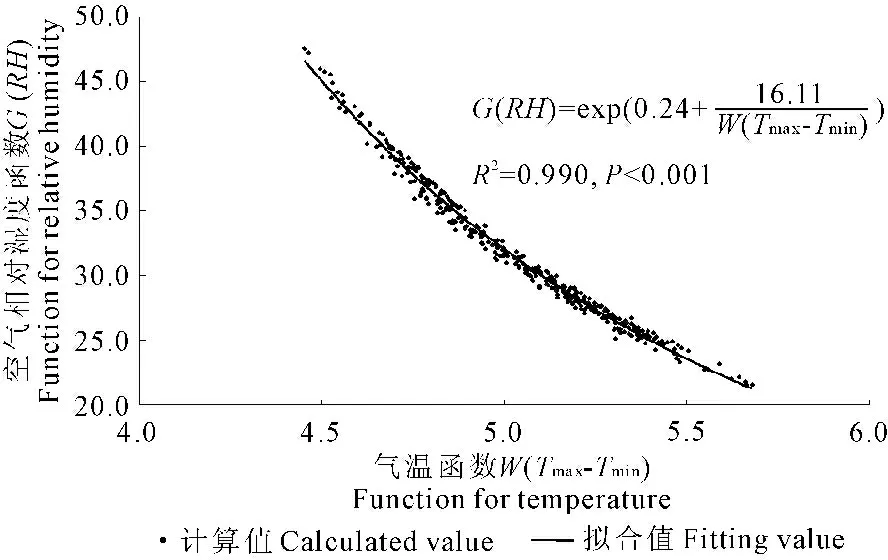
圖1空氣相對濕度與氣溫函數之間的關系

Fig.1 Functions of relative humidity and air temperature

從圖1中可以看出，特征氣溫函數W(Tmax-Tmin)與空氣相對濕度函數G(RH)之間存在較好的S關系。據此可推求計算RH(空氣相對濕度)的方法，見下式：

RH=(Tmax-Tmin)exp[0.24+

(8)

將典型灌區多年日均溫差代入式(8)，得空氣相對濕度估算值。與實測值比較表明，當溫差小于5℃時，按照式(8)計算的部分空氣相對濕度超過100%，與實際情況不符。大量分析表明，典型灌區日溫差小于5℃的天數一般年份不超過30 d，且當日溫差小于5℃時，空氣相對濕度平均值在89%左右，且偏差較小。因此，對式(8)作進一步分段計算如下：

(9)

根據典型灌區2011年實測空氣相對濕度，以及天氣預報提供的未來10 d最高氣溫和最低氣溫，對式(9)的計算精度進行驗證，見圖2。

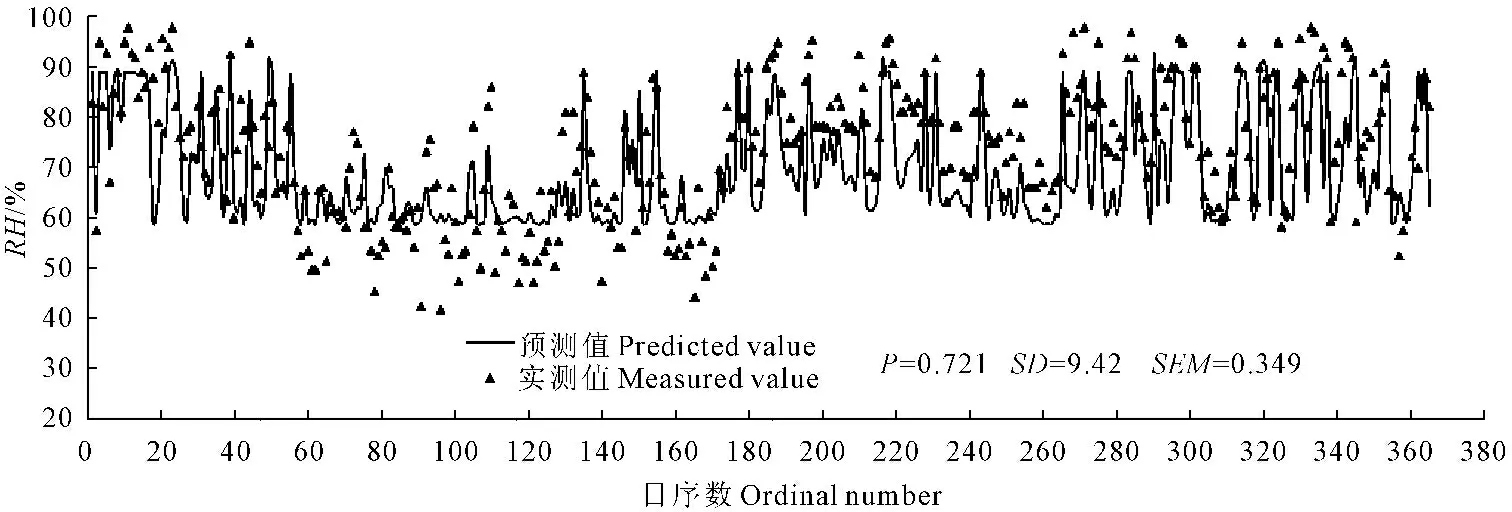
圖2典型灌區空氣相對濕度預測(2011年)

Fig.2 Predicted values of relative humidity in typical irrigation area at 2011

從圖2中可以看出，典型灌區2011年空氣相對濕度實測值和預測值之間相關系數為0.728，檢驗為極顯著相關，標準偏差為9.06，標準誤差為0.474。其中，標準偏差相對較大，且集中體現在3—5月份。初步分析認為，該時段典型灌區風速相對較大，而本文研究并未考慮風速的影響，致使該階段空氣相對濕度實測值和預測值之間差異相對較大。但對二者均值比較認為，實測值與計算值之間并不存在顯著差異。因此，本文采用式(9)作為預測空氣相對濕度的預測方法，解決預報ET0基礎參數難以直接獲取的問題。

2.2 改進Valiantzas方程

以典型灌區1993—2010年逐日相關數據為基礎，采用Penman-Monteith方法計算逐日ET0，并采用多元回歸方法確定式(7)的待定系數：a=0.159，b=-1.308，c=0.045，相關系數為0.986。計算結果見圖3。

綜上分析，改進的Valiantzas方程可表示為：

(10)

從上式可以看出，改進Valiantzas方法包括5個輸入參數，分別是日最高氣溫、日最低氣溫和平均氣溫，以及日序數、研究區地理緯度。其中，氣溫數據可以從常規天氣預報等信息平臺獲取。

2.3 方法驗證

為驗證上述模型在典型灌區的應用效果，采用Penman-Monteith方法計算了典型灌區2011年逐日ET0值，并以典型灌區2011年1月1日為起點，以天氣預報提供的未來10 d(如1月1日至1月10日)的逐日最高、最低氣溫作為輸入，結合式(9)空氣相對濕度預測方法，采用式(13)計算逐日ET0預測值，同時與潘云等修正的Valiantzas方法進行比較，見圖4。

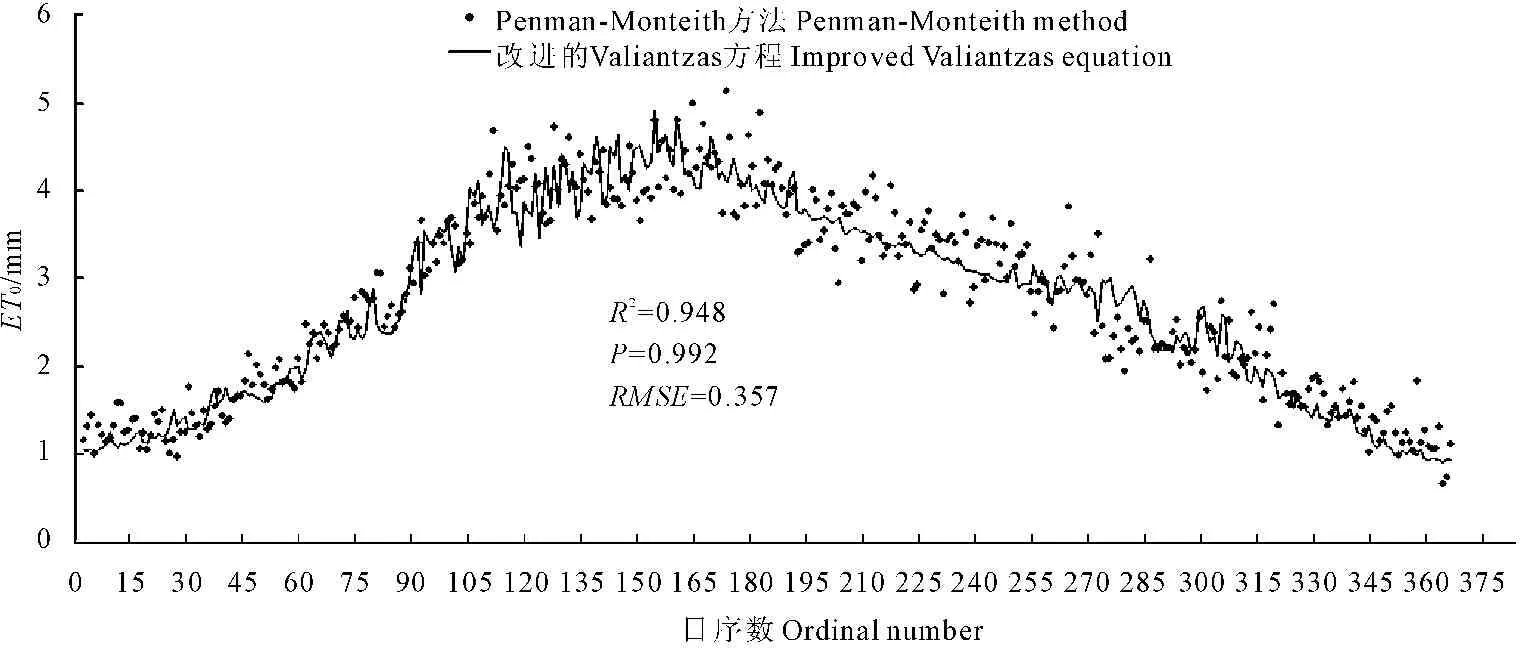
圖3改進的Valiantzas方程預測多年平均逐日ET0(2005—2010年)

Fig.3 The average dailyET0by improved Valiantzas equation(2005—2010)

與Penman-Monteith方法相比，本文研究改進Valiantzas方程和潘云修訂的Valiantzas方法計算ET0的均差、相對誤差、均方根偏差和相關系數如表1所示。從表中可以看出,二者計算結果均與P-M方法計算結果呈極顯著相關，但改進的Valiantzas方程相關系數更高。與原方程相比，改進Valiantzas方程在預測典型灌區2011年的ET0相對誤差減少12.4%，均方根誤差降低37.4%，相關系數提高13.4%。因此,改進的Valiantzas方法的預測精度明顯高于原方程，能夠更好地預測典型灌區參考作物需水量變化過程。同時，本文改進的Valiantzas方法以目前天氣預報可提供的日最高氣溫、最低氣溫、平均氣溫為主要輸入參數，能夠實現對參考作物需水量的中期預報(3～10 d)，與黃河水量旬調度要求提供未來10 d逐日作物需水量等基礎數據的實際需求一致。

圖4 ET0計算和預測結果

注：**表示極顯著相關。

Note: ** highly significant.

3 討 論

在氣象資料缺乏情況下，FAO推薦以氣溫為主要輸入的Hagreaves方法計算參考作物需水量，但該方法在風速高于3 m·s-1和空氣相對濕度較高的情況下容易產生對ET0計算的誤差[5]，并不適合黃河下游灌區的應用條件。茆智等[2]建立的逐日均值修正模型需要長系列基礎數據確定天氣類型修正系數，但以灌區為單元的歷史氣象資料難以對“曇、陰”等天氣類型作出精確判斷。本文在潘云等學者研究的基礎上，采用常規天氣預報提供的氣溫數據，建立了估算空氣相對濕度的方法，進一步降低了Valiantzas方程輸入參數種類，構建了適合典型引黃灌區的ET0計算和預測方程。本文采用的多元回歸方法雖然提高了Valiantzas方程在典型灌區的預測精度，但由于經驗系數需要結合當地氣候、地理等條件確定，應用于其它區域時，需要重新確定相應的待定系數。因此，下一步應結合空氣動力學、數值模擬等方法，開展參考作物需水量預測方法的通用性研究，以期更精確地應用于不同區域作物需水量預測，更好地服務于黃河水量精細調度，并為引黃灌區灌溉水資源需求研判等提供基礎數據支撐。

4 結 論

本文在分析Valiantzas方程及其改進方法計算ET0的基礎上，確定出采用改進方程計算ET0的主要輸入參數為特征氣溫和空氣相對濕度。其中，中期天氣預報能預報特征氣溫(最高氣溫、最低氣溫、日均氣溫)，但目前尚未實現對空氣相對濕度的量化預報。為解決空氣相對濕度量化預報技術的問題，本文以河南省柳園口灌區1993—2010年逐日最高氣溫、最低氣溫、空氣相對濕度等數據為基礎，研究建立了空氣相對濕度預測的方法。采用2011年相關數據驗證表明，本文研究建立的空氣相對濕度計算方法能夠反映典型引黃灌區逐日空氣相對濕度變化過程。此外，對潘云等人修正的Valiantzas方程進行了改進，根據典型引黃灌區的多年逐日ET0變化特征，分析確定了修正Valiantzas方程的多元回歸方程。以常規天氣預報提供未來10 d的特征氣溫數據作為主要輸入，采用Penman-Monteith方法計算的2011年逐日ET0值作為標準值，分析了本文研究提出改進Valiantzas方程的計算精度。分析認為，本文研究改進的Valiantzas方程的相對誤差、均方根誤差等均低于已有修正Valiantzas方法，且相關系數也相對較高。因此，改進的Valiantzas方程可實現基于常規天氣預報的灌區參考作物需水量預測，符合黃河水量精細調度的實時性、精確性、差異性、動態性的要求[18]，能夠為黃河水量旬調度方案編制提供技術支撐，并可以為灌區作物灌溉需水量的中期預報提供基礎數據支持。

參考文獻：

[1] 李國英.努力實現黃河功能性不斷流[N].黃河報，2008-1-26.

[2] 茆 智，李遠華，李會昌.實時灌溉預報[J].中國工程科學，2002，4(5):24-33.

[3] 彭世彰，胡 玲，張利昕.國內外灌溉預報研究現狀與動態分析[J].灌溉排水學報，2004，23(4)：6-10.

[4] 景 明，程獻國，王軍濤，等.黃河下游引黃灌溉需水預測關鍵技術分析[J].水資源與水工程學報，2013，24(6):60-63.

[5] Allen R G, Pereira L S, Raes D, et al. Crop evapotranspiration: Guide lines for Computing Crop Water Requirements[M]. Rome: United Nations FAO， Engineering，2003，129(1):53-63.

[6] 羅 毅，雷志棟，楊詩秀.潛在騰發量的季節性變化趨勢及概率分布特性研究[J].水科學進展，1997，8(4):308-312.

[7] 羅玉峰，崔遠來，蔡學良.參考作物騰發量預報的傅立葉級數模型[J].武漢大學學報(工學版)，2005，38(6):45-48.

[8] Valiantzas J D. Simplified versions for the Penman evaporation equation using routine weather data[J]. Journal of Hydroloy， 2006，331:L:690-702.

[9] 羅玉峰，李 思，彭世彰，等.基于氣溫預報和HS公式的參考作物騰發量預報[J].排灌機械工程報，2013，31(11):987-992.

[10] Luo Yufeng, Chang Xiaomin, Peng Shizhang, et al. Short-term forecasting of daily reference evapotranspiration using the Hargreaves-Samani model and temperature forecasts[J]. Agricultural Water Management，2014，(36):42-51.

[11] 趙 琪，羅玉峰，彭世彰，等.基于天氣預報和Penman-Monteith公式的短期逐日參考作物騰發量預報[J].節水灌溉，2014，(1):1-4.

[12] Perera K C, Western W A, Nawarathna B, et al. Forecasting daily reference evapotranspiration for Australia using numerical weather prediction outputs[J]. Agric Forest Meteorol, 2014,(194):50-63.

[13] 謝梅香，羅玉峰，錢子嘉，等.基于氣溫預報和神經網絡的參考作物騰發量預報[J].節水灌溉，2015，(2):33-36.

[14] Luo Yufeng, SeydouTraore, XinweiLyu, et al. Medium range daily reference evapotranspiration forecasting by using ANN and public weather forecasts[J]. Water Resources Management，2015，9(10):3863-3876.

[15] 徐冬梅，常向前，王路平，等.灌區水資源實時調度研究與應用[M].鄭州：黃河水利出版社，2007：61-63.

[16] Lewis T, Lamoureux S F. Twenty-first century discharge and sedinent yield predictions in a small high Arctic watershed[J]. Global and Planetary Change，2010，71(1/2):27-41.

[17] 潘 云，宮輝力，李小娟，等.蒸散發模擬的Valiantzas方法在中國的應用[J].水科學進展，2011，22(1):30-37.

[18] 蘇茂林.黃河水資源精細調度研究[J].人民黃河，2007，29(1)：1-2，60.

[19] Priestly C H B, Taylor R J. On the assessment of surface heat and evaporation using large-scale parameneters[J]. Mon Weather Rev，1972，100:81-92.

[20] Hargreaves G H, Allen R G. History and evaluation of Hargreaves evapotranspiration equation[J]. Journal of Irrigation and Drainage Engineering，2003，129(1):53-63.

[21] 翁篤鳴.中國輻射氣候[M].北京：氣象出版社：1997:26-37.