考慮嚙合齒對失效相關性的齒輪系統可靠性評估

白恩軍, 謝里陽, 胡杰鑫

(1.東北大學機械工程與自動化學院, 110819, 沈陽;2.東北大學航空動力裝備振動及控制教育部重點實驗室, 110819, 沈陽)

齒輪傳動系統在當今的機械裝備中大量應用,是應用最廣泛的機械傳動方式。齒輪系統疲勞可靠性的分析與建模方法已受到很多關注,并提出了很多理論和方法[1-4]。在齒輪傳動過程中,任意一個輪齒的失效都會影響齒輪系統的正常工作,從而導致齒輪傳動系統的失效,因而齒輪傳動系統是一個串聯系統。在傳統的可靠性分析研究中,齒輪多是被當作獨立失效的零件,或是將齒輪作為一個由各個失效因素組成的簡單的串聯系統來分析計算系統的可靠度[5-9],也有學者引入相關系數建立了考慮失效相關性的齒輪系統可靠性模型[10-13]。

系統在隨機輸入扭矩載荷作用下,同一時刻工作齒對的失效均是由共同扭矩載荷作用造成的,因此這些齒對的失效具有統計相關性,而在不同時刻,不同嚙合齒對所承受的扭矩載荷具有隨機性,因此,不同時刻不同工作齒對之間的失效不具有統計相關性。例如在時刻t1,扭矩載荷為T1,工作齒對為A1B1,這對輪齒的失效是統計相關的,在時刻t2,扭矩載荷為T2,工作齒對為A2B2,這對輪齒的失效也是統計相關的,但在這2個不同時刻,扭矩載荷具有隨機性,所以A1B1與A2B2間的失效不具有統計相關性。

本文以齒輪的齒根彎曲和齒輪接觸靜強度失效模式為例進行可靠性分析,分析中考慮了相互嚙合輪齒的失效相關性和齒輪嚙合的時變特性,基于蒙特卡羅抽樣方法編寫了多種失效模式下的齒輪系統可靠性仿真程序,并與傳統的串聯系統可靠性分析方法做了對比分析。本文方法避免了考慮嚙合齒對的失效相關性和時變嚙合特性的復雜建模過程,通過簡單的分析即可得到可靠的結果。

1 齒輪傳動系統的工作特點

齒輪傳動系統在系統與零件之間的關系上與傳統意義上的串聯系統有明顯的不同。齒輪傳動系統工作上是連續的,但并不是所有輪齒同時參與傳動,是一種多狀態的系統,而在傳統的串聯系統中,認為齒輪是一個獨立失效的零件,并沒有認識到齒輪系統是隨時間改變的多狀態系統,并在可靠度計算中將每個零件的可靠度簡單相乘來評估系統可靠度。齒輪傳動系統中的一對輪齒在完成嚙合后,在下一時刻均不參與工作,當這對輪齒再次嚙合時,已經轉過1周甚至幾周,并且每對輪齒在共同載荷作用下,它們之間的失效具有統計相關性。因此,在傳統可靠性建模中,把具有失效相關性的嚙合齒對中的每個輪齒看作獨立失效的零件處理,顯然是不切合實際的,故在齒輪可靠性分析中,需要考慮齒輪嚙合的失效相關性與時變特性。

2 多種失效模式下的傳統齒輪可靠性模型

在傳統的齒輪可靠性分析計算中,多是將齒輪或者每個輪齒作為一個獨立失效的零件。當零件存在多種失效模式時,任何一種失效都將導致零件的失效。因此,具有多種失效模式的零部件的可靠度可等效為由多種失效模式組成的串聯系統的可靠度。根據應力-強度干涉理論,具有多種失效模式的零部件在n次載荷作用下的可靠度可表示為

(1)

式中:Ri為零部件對應于失效模式i的可靠度;f(s)為應力s的概率密度函數;f(δ)為強度δ的概率密度函數。

如果將齒輪簡化為一個輪齒,假設齒輪扭矩載荷為T,其概率密度函數為f(T),則齒輪在多種失效模式下n次載荷作用時的齒輪可靠度[14]為

(2)

式中:h(T)=n[F(T)]n-1f(T)為輪齒承受的n次載荷中的最大次序統計量的概率密度函數,其中F(T)為輪齒載荷累積分布函數;si(T)為失效模式i在載荷T作用下的失效應力;Fi為失效模式i在載荷T作用下的失效概率;m為失效模式數。

如果將齒輪的每個輪齒作為獨立失效的零件,則具有z個輪齒的齒輪可靠度表示為

(3)

由式(3)可知,傳統的齒輪可靠性分析中將齒輪或者輪齒作為獨立失效的零件,既沒有考慮相互嚙合齒輪失效的統計相關性和失效模式的相關性,也沒有反映出齒輪傳動的時變多狀態特點。

3 考慮時變特性及多種失效模式的齒輪可靠性分析方法

齒輪存在齒面接觸失效和齒根彎曲失效等多種失效模式,由文獻[15-16]可知,在共同扭矩載荷作用下,相互嚙合輪齒的失效以及各失效模式間具有失效統計相關性。假設相互嚙合的2個輪齒的齒根彎曲強度和齒面接觸強度的分布函數分別為ft1(δ)、ft2(δ)和fc1(δ)、fc2(δ),在共同扭矩載荷f(T)的1次作用下,不考慮失效相關性時的可靠度可表示為

(4)

當考慮失效相關性時,可靠度表示為

(5)

從式(4)、式(5)可知,考慮共因失效與否這對輪齒的可靠度是不同的,即R1≠R2。因此,在相同載荷作用下,無論是相互嚙合輪齒的各種失效模式間,或是一個輪齒的各種失效模式間,均具有統計相關性,并不能認為各個零件的失效是相互獨立的。在式(2)與式(3)中,認為各個失效模式間相互獨立,而沒有考慮一個輪齒的多種失效模式間的統計相關性和相互嚙合輪齒的各失效模式間的統計相關性。

輪齒在工作過程中,齒輪嚙合的時變性很難通過傳統方法建模。假設2個齒輪的齒數分別為2和3(這里之所以選用齒數為2和3的齒輪舉例,是因為齒數少易于辨別一個嚙合周期,即輪齒1vs1再次嚙合,使過程清晰明了),則這對齒輪從編號為1vs1的輪齒開始嚙合,經過2vs2、1vs3、2vs1、1vs2、2vs3,再次回到1vs1嚙合。那么,這對齒輪在載荷歷程T的n次作用下每對輪齒的可靠度符號如表1所示。

表1 齒對嚙合順序及對應的可靠度符號

在計算嚙合齒對1vs3的可靠度時,由于嚙合齒對1vs1在經歷過的載荷作用下沒有失效,因此齒對1vs1的2個齒的強度需要修正為后驗強度分布[17],進而計算在齒對1vs1不失效的條件下1vs3的條件概率R1vs3|1vs1(n),其他嚙合齒對的條件概率計算方法與此相同。最終,這對輪齒在載荷歷程T的n次作用下的系統可靠度為這些嚙合齒對可靠度的乘積。

由此可見,由齒數為2和3的齒輪組成的傳動系統的可靠度需要計算6個齒對的可靠度。如果組成傳動系統的嚙合齒對很多,再考慮多種失效模式,則對傳動系統進行可靠性建模的難度顯而易見,因此極有必要尋找一種簡單的分析方法。利用蒙特卡羅抽樣方法,可以很容易實現考慮多種失效模式和齒輪嚙合時變性的可靠性分析方法。

3.1 齒輪的時變嚙合關系

確定嚙合齒對時變嚙合關系的方法如下。

令齒輪的重合度為1(實際重合度大于1。在齒輪傳動過程中,無論齒輪的重合度為多少,齒輪輪齒均由逐漸嚙入到逐漸退出嚙合,在此過程中,齒面接觸應力和齒根彎曲應力均出現一次最大值,這里簡化為每個輪齒嚙合過程中的最大齒面接觸應力和齒根彎曲應力,故令重合度為1)。

假設一個兩級傳動的齒輪傳動系統如圖1所示,齒輪Z1、Z2、Z3和Z4的齒數分別為11、36、11和62。令齒輪Z1的各齒編號為1～11,Z2、Z3和Z4均按此方法編號。

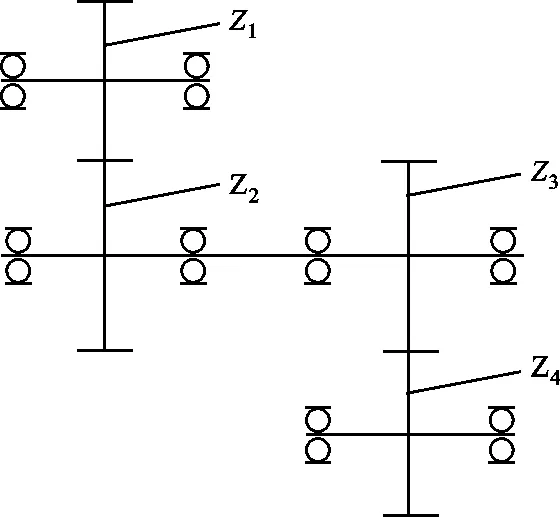
圖1 齒輪系統示意圖

令一級傳動齒輪Z1與Z2從編號1vs1開始嚙合,依次經過2vs2,…,11vs11,1vs12,…,3vs36,…。當齒輪載荷作用次數n≤Z1時,嚙合齒對為nvsn;當Z1Z2時,嚙合齒對為(n-[n/Z1]Z1) vs (n-[n/Z2]Z2)。嚙合齒對的對應關系可以表示為

(6)

式中:如果n-[n/Z1]Z1=0,則令n-[n/Z1]Z1=Z1;如果n-[n/Z2]Z2=0,則令n-[n/Z2]Z2=Z2。

對于同軸上的齒輪Z2和Z3,由于齒數不同,當齒輪Z2轉過一個齒時,齒輪Z3并沒有轉過一個齒(齒數相同時,可以直接用式(6)表示)。假設θ2和θ3分別為齒輪Z2和Z3完成一次嚙合的轉角,由齒輪嚙合線長公式計算

(7)

式中:B1B2=επmcosα為齒輪實際嚙合線段,其中ε為重合度,m為模數,α為壓力角;rb為基圓半徑。

當齒輪Z2完成一次嚙合,齒輪Z3完成了θ2/θ3次嚙合,則一級與二級之間的時變嚙合關系為

(8)

式(8)可以近似表示同軸2個齒輪之間的嚙合次數關系。當同軸上有更多齒輪時,均可以用該式計算。將式(8)中的n代入式(6),即可得到二級齒輪的齒對時變嚙合關系。

3.2 齒輪傳動系統可靠性仿真方法

在靜強度可靠性建模中,當接觸齒對的應力大于該齒的強度時,齒輪即發生破壞。因此,本文中的齒輪靜強度失效判斷準則為接觸齒對的計算應力σ大于該齒的強度δ,即

σ>δ

(9)

當齒輪為接觸失效時,σ和δ分別為計算接觸應力和接觸強度;當齒輪為彎曲失效時,σ和δ分別為計算彎曲應力和彎曲強度。

假設齒輪系統的輸入扭矩載荷考慮了傳動中的振動、沖擊及時變剛度等影響因素。根據齒輪傳動系統的特點以及可靠性建模方法,以齒面接觸失效和齒根彎曲失效為例,本文方法的技術路線如下:

(1)輸入扭矩、齒面接觸強度分布、齒根彎曲強度分布、樣機總數和齒輪等參數;

(2)選擇一個齒輪系統樣本,通過隨機抽樣方法隨機產生每個輪齒的齒面接觸強度和齒根彎曲強度,從而生成具有強度信息的系統樣本;

(3)通過隨機抽樣確定某一時刻的輸入扭矩載荷,并根據齒輪的時變嚙合關系確定此時刻的嚙合齒對,根據ISO齒輪標準計算扭矩T下所有參與嚙合齒對的應力σ(接觸應力和彎曲應力);

(4)當σ≤δ時,返回到步驟(2),當σ>δ時,記錄載荷作用次數n,n即為該齒輪系統樣本的壽命。

重復以上步驟,可以得到在輸入載荷下指定壽命的失效樣本數Nf,再利用Nf與樣本總數的比值(失效概率)即可計算出系統的可靠度,或在指定樣本數下檢驗所有失效數據的壽命分布,根據壽命分布來計算系統的可靠度。

該技術路線的仿真流程如圖2所示。

圖2 齒輪系統可靠性仿真流程圖

4 驗證與分析

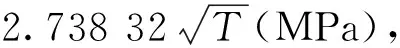
(10)

式中:h(T)=n[F(T)]n-1f(T)為輪齒承受的n次載荷中的最大次序統計量的概率密度函數,其中F(T)為輪齒載荷累積分布函數,f(T)為載荷T的概率密度函數;j為齒輪輪齒編號;g為齒輪的齒數;m為失效模式;k為失效模式數;f(δ)為齒輪強度δ的概率密度函數。

驗證模型在計算嚙合齒對jvsj的可靠度時,計算了該對輪齒的所有失效模式的可靠度(假設2種失效模式:接觸失效和彎曲失效),考慮了嚙合齒對的統計失效相關性。

通過式(10)(驗證模型)和本文方法計算這對齒輪的可靠度,結果如圖3所示。

圖3 齒輪系統可靠度仿真方法驗證

由圖3可知,在考慮了齒輪嚙合時變特性和失效相關性后,本文方法與驗證模型的計算結果是一致的。

對于更為復雜的不同齒數的齒輪組,通過數值公式建模時需按表1所示方法進行,難度很大,而在本文所提出的仿真方法中,嚙合關系是確定的,對于不同形式的齒輪組合(如風機行星齒輪組與外嚙合齒輪組成的多級齒輪復雜系統),只需建立嚙合齒輪的嚙合關系。

由圖4可知:當載荷作用107次時,方法1計算的齒輪系統的可靠度為0.493 6,方法2計算的可靠度為0.083 7,本文方法計算的可靠度為0.103 6。顯然,方法1計算的可靠度高估了45.99%,而方法2計算的可靠度低估了19.21%。

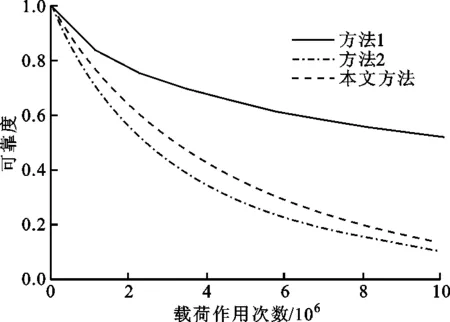
圖4 3種方法計算的齒輪系統算例的可靠度

由算例可知,由于方法1和方法2將齒輪或輪齒看作獨立失效的零件,各失效模式間均相互獨立,所以方法1高估了齒輪系統的可靠度,而方法2低估了齒輪系統的可靠度。本文方法考慮了嚙合齒對的失效相關性和嚙合時變性,分析方法更加貼合實際,計算結果更加趨于合理。在考慮載荷微觀不確定性的情況下,隨著載荷作用次數的增加,方法1與方法2估算的系統可靠度相對于本文方法的結果偏差更大。

5 結 論

相互嚙合的齒輪具有失效相關性與嚙合時變性,通過數值建模方法分析齒輪系統的可靠度時應當考慮這2個因素,但這會使建模和分析過程變得復雜。本文基于蒙特卡羅抽樣方法,在考慮相互嚙合輪齒的失效相關性和齒輪嚙合時變特性的同時,簡化了齒輪系統的可靠性分析方法。新方法將齒輪重合度簡化為1,與傳統的應力-強度干涉方法是一致的,適用于可靠度計算。本文的研究獲得以下結果和結論。

(1)根據齒輪嚙合的時變特性,給出了齒輪時變嚙合關系式。

(2)基于蒙特卡羅抽樣方法,提出了考慮多種失效模式下嚙合齒對失效相關性與嚙合時變性的齒輪系統可靠性分析方法。由于傳統方法未考慮多失效模式下嚙合齒對的失效相關性和嚙合時變性,所以相比本文方法會高估或低估齒輪系統的可靠度。

(3)本文方法雖是基于外嚙合的一般齒輪傳動系統,但對于包括內嚙合齒輪和雙側受載行星齒輪的風機齒輪傳動系統等更為復雜的齒輪系統,也可應用本文方法評估齒輪系統的可靠性。

參考文獻:

[1] 林小燕, 魏靜, 賴育彬, 等. 基于非線性疲勞損傷累積理論的齒輪傳動剩余強度模型及其動態可靠度 [J]. 哈爾濱工程大學學報, 2017(2017-04-27)[2017-08-20]. http:∥www.doc88.com/p-5307498769541. html.

LIN Xiaoyan, WEI Jing, LAI Yubin, et al. Residual strength model of gear transmission based on nonlinear fatigue damage accumulation theory and its dynamic reliability [J]. Journal of Harbin Engineering University, 2017(2017-04-27)[2017-08-20]. http:∥www.doc88.com/p-5307498769541.html.

[2] BENKAMRA Z, TERBECHE M, TLEMCANI M. Bayesian sequential estimation of the reliability of a parallel-series system [J]. Applied Mathematics and Computation, 2013, 219(23): 10842-10852.

[3] HUANG Xianzhen, HU Sen, ZHANG Yimin, et al. A method to determine kinematic accuracy reliability of gear mechanisms with truncated random variables [J]. Mechanism and Machine Theory, 2015, 92: 200-212.

[4] XIE Liyang, WU Ningxiang, QIAN Wenxue. Time domain series system definition and gear set reliability modeling [J]. Reliability Engineering & System Safety, 2016, 155: 97-104.

[5] 胡青春, 段福海, 吳上生. 封閉行星齒輪傳動系統的可靠性研究 [J]. 中國機械工程, 2007, 18(2): 146-149.

HU Qingchun, DUAN Fuhai, WU Shangsheng. Research on reliability of closed planetary transmission systems [J]. Chinese Mechanical Engineering, 2007, 18(2): 146-149.

[6] ZHOU Di, ZHANG Xufang, ZHANG Yimin. Dynamic reliability analysis for planetary gear system in shearer mechanisms [J]. Mechanism and Machine Theory, 2016, 105(11): 244-259.

[7] AZIA E, CHASSAPIS C. Comparative analysis of tooth-root strength using stress-strength interference (SSI) theory with FEM-based verification [J]. International Journal on Interactive Design and Manufacturing, 2014, 8(3): 159-170.

[8] NEJAD A R, GAO Z, MOAN T. On long-term fatigue damage and reliability analysis of gears under wind loads in offshore wind turbine drivetrains [J]. International Journal of Fatigue, 2014, 61(4): 116-128.

[9] 秦大同, 周志剛, 楊軍, 等. 隨機風載作用下風力發電機齒輪傳動系統動態可靠性分析 [J]. 機械工程學報, 2012, 48(3): 1-8.

QIN Datong, ZHOU Zhigang, YANG Jun, et al. Time-dependent reliability analysis of gear transmission system of wind turbine under stochastic wind load [J]. Journal of Mechanical Engineering, 2012, 48(3): 1-8.

[10] NAVARRO J, DURANTE F. Copula-based representations for the reliability of the residual lifetimes of coherent systems with dependent components [J]. Journal of Multivariate Analysis, 2017, 158(6): 87-102.

[11] 劉波, 安宗文. 考慮零件壽命相關的風電齒輪箱可靠性分析 [J]. 機械工程學報, 2015, 51(10): 164-171.

LIU Bo, AN Zongwen. System reliability analysis of wind turbine gearbox considering component life dependency [J]. Journal of Mechanical Engineering, 2015, 51(10): 164-171.

[12] 陳文華, 鄭朝朋, 李奇志, 等. 基于Copula函數的2.5 MW風電齒輪箱齒輪可靠性分析 [J]. 工程設計學報, 2015, 22(5): 425-430.

CHEN Wenhua, ZHENG Zhaopeng, LI Qizhi, et al. Gear reliability analysis of 2.5 MW wind turbine gearbox based on Copula function [J]. Chinese Journal of Engineering Design, 2015, 22(5): 425-430.

[13] ERYILMAZ S. Multivariate Copula based dynamic reliability modeling with application to weighted-k-out-of-nsystems of dependent components [J]. Structural Safety, 2014, 51(11): 23-28.

[14] XIE L Y, ZHOU J Y, WANG Y Y, et al. Load-strength order statistics interference models for system reliability evaluation [J]. International Journal of Performability Engineering, 2005, 1(1): 23-36.

[15] 謝里陽, 王正, 周金宇, 等. 機械可靠性基本理論與方法 [M]. 北京: 科學出版社, 2009: 271-283.

[16] 周志剛, 徐芳. 考慮強度退化和失效相關性的風電齒輪傳動系統動態可靠性分析 [J]. 機械工程學報, 2016, 52(11): 80-87.

ZHOU Zhigang, XU Fang. Dynamic reliability analysis of gear transmission system of wind turbine considering strength degradation and dependent failure [J]. Journal of Mechanical Engineering, 2016, 52(11): 80-87.

[17] 謝里陽, 林文強. 基于載荷-強度關系的失效率離散建模方法及模型 [J]. 機械強度, 2010(4): 10-15.

XIE Liyang, LIN Wenqiang. Failure rate modeling method based on load-strength relationship [J]. Mechanical Strength, 2010(4): 10-15.