基于最優控制的舵鰭聯合減搖性能指標函數的分析研究

鄒令輝，周 崗，李文魁，陳永冰，殷波蘭

(1. 海軍工程大學 電氣工程學院，湖北 武漢 430033；2. 中國人民解放軍91630部隊，廣東 廣州 510320)

0 引 言

隨著船舶航運業的發展，對船舶航行控制的要求也越來越高，目前針對船舶航向航跡控制的理論研究及工程實踐已得到較大發展,國內船舶上已經開始廣泛裝備航跡自動航行控制系統[1–3]。該系統主要對船舶的首向和航跡軌跡進行控制，未對船舶首向與橫搖進行綜合控制。研究表明船舶操舵控制也可以產生減搖效果，因此只進行首向和航跡控制沒有充分發揮操舵和減搖鰭的綜合控制效能。由于船舶在大海中航行，風浪流的干擾產生橫搖運動會造成船舶航行穩定性下降，直接影響航行安全。如何有效的在船舶航向航跡控制的同時進行舵和鰭的減搖綜合控制目前是船舶操縱控制的研究熱點之一[4–5]。

在20世紀70年代，Cowley和Lambert提出了舵減搖的設想[6]。隨后，舵減搖便在一商船上試驗成功，但其減搖效果最多達到50%。由于橫搖與首搖存在耦合，1981年，Kallstrom提出舵鰭聯合減搖，采用多變量線性二次型控制理論進行控制，取得了更好的減搖效果[7]。1999年，Sgobbo和Parsons利用美國海岸警衛隊901級艦現有的舵/鰭傳動機構，對4種控制器進行仿真，發現在不改變現有舵機設備下，舵鰭聯合減搖控制器的減搖效果最佳[8]，該控制器采用的是最優狀態反饋控制理論。該文沒有深入討論如何選取最優狀態反饋控制的性能指標函數，其給出的權系數矩陣中的參數較多，這些參數的改變會直接影響舵鰭聯合減搖控制器的控制性能，現有文獻中較少涉及權系數矩陣如何影響舵鰭聯合減搖控制性能，因此有必要研究如何選擇性能指標函數的問題，以及權矩陣參數影響控制器減搖性能的規律。

本文對船舶運動的三自由度數學模型，根據最優控制理論設計了舵鰭聯合減搖控制器并在海浪干擾下進行數字仿真，結果表明控制器減搖性能良好。同時，在工程實際應用中，還沒有對設計舵鰭聯合減搖控制器時性能指標函數中權矩陣參數如何選取的研究。本文參考船舶航向控制中控制器設計時權矩陣系數的選擇范圍，經過仿真研究，得到了權矩陣參數對控制器減搖性能的影響，研究內容具有一定的理論意義和工程應用價值。

1 船舶運動三自由度模型

船的運動方程通常需要一個固定在船上的坐標系來表達。其坐標原點選擇為船中的設計水線面和中線面處。船舶運動一般有縱蕩、橫蕩、升沉、首搖、橫搖、縱搖6個自由度，其中用于研究船舶減橫搖中的一般為橫蕩、首搖和橫搖，分別用v，?，ψ，p，r表示橫蕩速度，橫搖角，橫搖角速度，縱搖角和縱搖角速度。

根據船舶運動原理，假定縱蕩運動的動態特性較其他幾個自由度要慢，航速和浪向角不變，將作用在船舶的水動力和力矩泰勒展開后，即可以得到關于橫蕩、橫搖和首搖這3個自由度的方程[9]：

式中：m為船舶質量；u為船速；xG，zG為船舶重心在坐標系中的坐標；Ixx，Izz為船舶繞x軸，z軸的質量慣性矩；為作用在船舶上與加速度項有關的水動力系數；分別為舵、鰭在3個方向上產生的控制力和力矩，為鰭角α和舵角δ的函數，具體形式可參考文獻[9]。均為水動力泰

勒展開式去掉與加速度項有關的系數項后的部分。

令狀態向量，輸 入為對非線性項在平衡點進行泰勒展開，并取展開式的第1項近似，由式（1）可得

其中：

式中：，均為作用在船舶上的水動力系數。

所以船舶的三自由度線性化的狀態空間模型為：

其中。

2 最優控制器的設計

當狀態方程表示的系統為可控或可鎮定時，令性能指標函數[10]為

則使取極小值的最優控制可表示為

為黎卡提方程的唯一正數半定解：

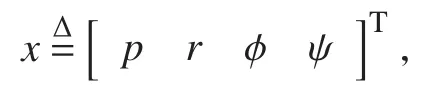
在設計最優控制器時，本文所選取的性能指標函數為

控制器性能由橫搖減搖效率衡量，定義如下：

式中，σ為未安裝控制器時的橫搖幅值標準差；σc為安裝了控制器時的橫搖幅值標準差。

3 仿真研究

本文主要以美海岸警衛隊WMEC910級艦為對象進行實驗模擬研究。該艦安裝了一對減搖鰭以及配備常規舵。根據文獻[9, 11]可得該艦的主要特性參數，對于狀態方程有：

鰭機的傳遞函數表示如下：

舵機的傳遞函數表示如下：

本文對海浪干擾采用一種簡單的模擬方法，用高斯白噪聲驅動1個二階振蕩環節，疊加在船舶數學模型的橫搖角輸出上。在6級風的情況下，海浪的傳遞函數為[12]

設計控制器時的狀態方程簡化為，

對于性能指標函數J，令可得到最優控制律為

圖1表明船舶在有無最優控制器情況下的仿真結果，可以看到有控制器的船舶的橫搖角明顯減小，說明了控制器具有良好的減搖性能。

為觀察對控制器性能的影響，采取控制變量法。

首先，為觀察λ?對控制器性能的影響，令則性能指標函數為對λ?賦值，得到最優控制律后對控制器進行仿真，控制器減搖效率與的關系如圖2所示，由圖可知當時，減搖效率最好；λ?減小時，減搖效率降低，并λ?減小到一定值后，反而會加大橫搖運動；當λ?增大時，減搖效率變低，增加到一定值后，也會加大橫搖運動。

同時，當λ?變化時，船舶首搖角變化如圖3所示，可以看出λ?增大時，首搖角幅度變大，但總體上對首搖角的影響較小。

其次，為觀察λα對控制器性能的影響，令則性能指標函數為對λα賦值，得到最優控制律后對控制器進行仿真，仿真時長t=50 000 s。控制器減搖效率與λ2（λ2=20 log10λα）的關系如圖4所示由圖可知當λα=0.21時，減搖效率最好；λα減小時，減搖效果急劇下降，甚至加大橫搖；λα增大時，減搖效率逐漸降低。

同時，當λα變化時，船舶首搖角變化如圖5和圖6所示，由圖5可以看出λα減小時，首搖角幅度變大，對首搖角的影響較大；并且當λα≤0.20時，由于橫搖與橫蕩之間存在耦合，控制會產生大的橫蕩速度，進而使船舶橫搖運動的加大并造成首搖控制發散。

再者，為觀察λδ對控制器性能的影響，令，則性能指標函數為，對λδ賦值，得到最優控制律后對控制器進行仿真,仿真時長t=50 000 s。λδ與控制器減搖效率的關系如表1所示，可以看出當λδ在3.95～4.20內時，減搖效率最好；λδ減小時，減搖效率逐漸降低；λδ增大時，無減搖效果，甚至加大橫搖運動。

同時，當λδ變化時，船舶首搖角變化如圖7所示，由于橫搖與橫蕩之間存在耦合，控制會產生大的橫蕩速度，進而使船舶橫搖運動的加大并造成首搖控制發散。

綜上所述，權系數λ?，λα，λδ對控制器減搖性能的影響為：

1）隨著權矩陣參數λ?的增大，控制器的減搖性能先逐漸提高到最大值而后降低；

2）隨著λα的減少減搖性能會提高，當減少到一定值時會造成減搖控制系統不穩定。

3）隨著λδ的增大減搖性能會逐漸提高，當增大到一定值時會造成減搖控制系統不穩定。

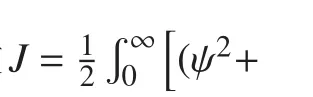
表1 λδ與控制器減搖效率的關系Tab. 1 Relationship of λδ and efficiency of roll stabilization

仿真表明其減搖效率η1=65.55%，相比得到的控制器減搖效率η=63.89%高1.66個百分點，說明按照所得的規律進行控制器的設計有效。但與此同時首搖角控制精度下降，所以在惡劣海況下對航向要求不高時，可采用此種控制律。

4 結 語

通過對船舶運動的3-DOF的數學模型設計的最優控制器進行仿真，得到了權矩陣參數變化對控制器減搖性能的影響規律，并驗證了權矩陣參數對控制器影響規律的有效性。本文只針對美海岸警衛隊910級進行仿真，所得到的關于性能指標函數中的的變化規律對其他船舶是否適用，這將是下一步研究的重點。

參考文獻：

[ 1 ]周崗, 李文魁, 陳永冰, 等. 基于最優控制的船舶航跡全局NPD控制算法[J]. 系統工程與電子技術, 2014, 36(1):143–148.ZHOU Gang, LI Wen-kui, CHEN Yong-bing, et al. Global NPD tracking control algorithm of ship based on optimum control theory[J]. Systems Engineering and Electronics, 2014,36(1): 143–148.

[ 2 ]周崗, 陳永冰, 陳陽, 等. 一種船舶直線航跡控制算法及控制參數的設計[J]. 儀器儀表學報, 2013, 34(5): 1043–1048.ZHOU Gang, CHEN Yong-bing, CHEN Yang, et al. Design of control algorithm and control parameters for ship straight-line tracking controller[J]. Chinese Journal of Scientific Instrument,2013, 34(5): 1043–1048.

[ 3 ]孫健, 陳永冰, 周崗, 等. 兩種響應性船舶運動模型的對比及適用性分析[J]. 艦船科學與技術, 2016, 38(6): 14–19.SUN Jian, CHEN Yong-bing, ZHOU Gang, et al. The Comparision and applicability analysis of two kinds of responding ship model[J]. Ship Science and Technology, 2016,38(6): 14–19.

[ 4 ]王新屏, 張顯庫. 具有航向保持非線性的舵鰭非線性魯棒控制[J]. 系統工程與電子技術, 2008, 30(8): 1549–1552.WANG Xin-ping, ZHANG Xian-ku. Nonlinear robust control for rudder /fin joint system with nonlinear course-keeping[J],Journal of Systems Ergineering and Electronics, 2008, 30(8):1549–1552.

[ 5 ]劉勝, 李高云, 方亮, 等. 船舶航向/橫搖魯棒控制研究[J]. 電機與控制學報, 2009, 13, 129–134.LIU Sheng, LI Gao-yun, FANG Liang, et al. Research on ship course/roll robust control[J], Electric Machines and Control,2009, 13, 129–134.

[ 6 ]COWLEY W E, LAMBERT T H. The use of rudder as roll stabilizer[C]//Proceeeding of SCSS72[C]. Bath, UK, 1972, 2.

[ 7 ]KALLSTROM C G. Control of yaw and roll by a rudder/fin stabilization system[J]. 6thShip Control System Symposium,Proc. Canada, 1981, 2, 3–1.

[ 8 ]SGOBBO J N, PARSONS M G. Rudder/Fin stabilization of the USCG WMEC 901 class vessel[J]. Marine Technology,1999.

[ 9 ]李棟良. 船舶舵/鰭聯合減搖的魯棒控制系統設計[D]. 哈爾濱: 哈爾濱工程大學, 2013.

[10]王青, 陳宇, 張穎昕, 等. 最優控制理論、方法與應用[M]. 北京: 高等教育出版社. 2011: 73–74.

[11]M G SARCH. Fin stabilizers as maneuver control surfaces[D].USA: Naval Postgraduate School, 2003: 7–19.

[12]WANG Xin-ping, ZHANG Xian-ku, ZHANG Li-kun.Comparison of H∞robust filter and kalman filter[J]. Systems Engineering and Electronics, 2003, 25(10): 1267–1269.