推動手推車的力學分析

劉凝 劉喜軍

[摘 要] 推與拉是一種常見的力學現象，在日常生活中人們也經常遇到。從早期的人力車、畜力車到爬陡坡用的雙頭機車，人們對推與拉哪個更省力都有親身的體驗。有趣的是，在教育的不同階段，關于推與拉省力的問題有著不同的解釋。在《推動手推車的力學分析》中，試圖把理論分析與日常經驗相結合，得出一個較為合理的解釋。通過力學中的整體法，《推動手推車的力學分析》提出了在日常生活中“推比較省力”的觀點。通過建立模型，進一步提出了在設定條件下“拉與推所用力相等”的觀點。“拉比較省力”的觀點，是初等教育背景下易得出的結論。“無法判斷”拉與推哪種方法省力，是一個高等教育之上的問題，《推動手推車的力學分析》并不能找出實例，沒有得出結論。

[關 鍵 詞] 摩擦力；力學模型；連接體

[中圖分類號] G642 [文獻標志碼] A [文章編號] 2096-0603（2018）13-0137-03

一、引言

2011年3月，筆者參加了“2011年第二十一屆全國初中應用物理競賽”。第一題是單項選擇題，其中第2小題為工人師傅用手推手運送純凈水的圖片（圖1），對這兩種方法中哪種方法比較省力的判斷，下列說法中正確的是（ ）

A.圖甲的方法比較省力

B.圖乙的方法比較省力

C.圖甲和圖乙兩種方法所用力的大小相等

D.無法判斷

筆者選擇了B，而競賽后公布的標準答案是A。當時，參加完競賽考試，回家后討論了拉與推的問題；現在，筆者于大學四年級寒假期間，對拉與推的問題做了盡可能系統的分析，形成了更為全面的初步結論。

二、基于克服摩擦力的“拉的方法省力”

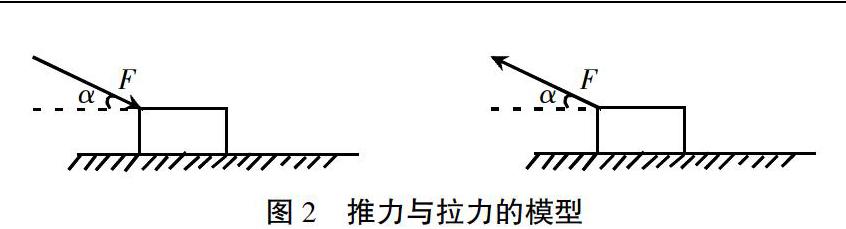
形成拉的方法省力的認識，肇始于對摩擦力的克服，需要有一個向上的分力。從向上分力有助于克服摩擦力的判斷，得出拉的方法省力的結論。（圖2）

三、基于克服阻力矩的“推的方法省力”

在使手推車運動的問題上，不是需要克服摩擦力，無論靜摩擦力，還是動摩擦力；而是需要克服滾動摩擦，即需要克服滾動形成的阻力，克服阻礙手推車小輪滾動的力矩。使手推車運動的力大小，由阻力矩決定，不是由靜摩擦力或動摩擦力決定。

同時，省力是對人而言，在使手推車運動的過程中，工人師傅付出的力的大小決定省力與否。在施加力于手推車之上時，存在重力問題。或者是手推車的重力由人承擔，這相當于拉的方法；或者是人的重力由手推車承擔，這相當于推的方法。判斷拉的方法是否省力，需要比較手推車與人這兩個相連的系統，看哪一個需要克服阻力的力更小。

一般認為，人的行走相當于多邊形的滾動，步幅的一半相當于阻力矩。從工人師傅用手推車運送純凈水的情景看，手推車是運動在起伏較小的水泥（或瀝青）路面上。手推車的阻力矩小于相當于步幅一半的人的阻力矩。得出手推車運動需要克服阻力的力更小，得出人的重力由手推車承擔更省力，得出推的方法更省力。反之，得出人需要克服阻力的力更大，得出手推車的重力由人承擔更費力，得出拉的方法更費力。

極端情況為，拉著手推車運動，向上角度增大，直到完全提起手推車，這相當于扛著手推車運動。推著手推車的極端情況為向下角度增大，直到完全壓在手推車上，這相當于坐在手推車上腳蹬著地運動。

四、基于重心無起伏模型的“拉與推所用力相等”

在理想狀態下，建立拉與推所用力相等的模型。

設路面無起伏，或者說起伏趨于無窮小。

對手推車，設定阻力矩為零，或者說趨于無窮小。得出重心運動軌跡與路面平行，得出手推車可以無阻力地運動。

對人的行走模型，具體如下：

（一）多邊形模型

一般認為，人的行走相當于多邊形的滾動。腿部被設定為單一剛桿。得出步幅的一半相當于阻力矩，阻力矩不為零，并較大。

（二）兩截剛桿腿部模型

行走的多邊形模型，其重心起伏較大，與實際行走情況差距較大，阻力矩太大。模擬實際行走，設置腿部為兩截剛桿。以此平緩多邊形模型的重心起伏，達到降低阻力矩的目的。

此兩截剛桿腿部模型（設兩截長度相等）的行走流程設定為：（1）起步。兩大腿平行，與重力夾角30°；左小腿與大腿成直線，右小腿與左小腿夾角60°。重心在右腿上。（2）重心移動。重心向前移動，腿部改變夾角。直到左大腿與重力夾角30°，小腿與重力夾角30°；右腿成直線，與重力夾角30°。重心在左腿上。（3）邁步。右小腿向前邁步，與左小腿夾角60°。重心仍在左腿上。與起步對稱。（4）重心移動。同（2），其中左腿變為右腿。（5）邁步。同（3），其中右腿變為左腿。

至此，經（2）重心移動—（3）邁步—（4）重心移動—（5）邁步，形成一個行走周期。接著可以繼續此周期。（1）起步與邁步對接；行走終止可中止于一個周期的任何一個環節，最后還原為起步狀態。

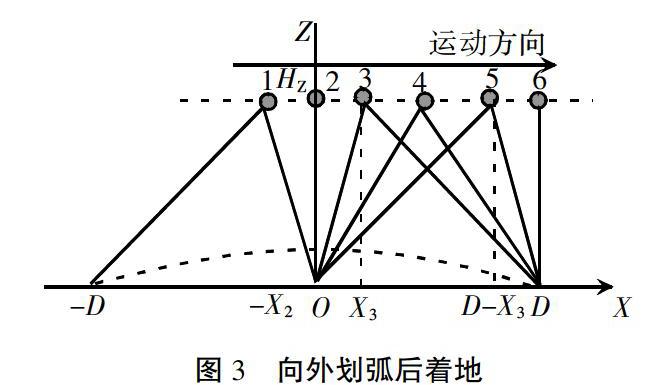
該兩截剛桿腿部模型的局限性，一是在重心移動環節，沒有設定“腿部改變夾角”的角度，無法避免重心起伏；二是在邁步環節，因為是簡化模型，沒有模擬人下肢的腳踝，邁步中表現為繞髖關節向外劃弧后著地（圖3）。

（三）連桿機構模型及拉與推手推車所用力相等

為克服兩截剛桿腿部模型的局限性，建立連桿機構模型。

1.連桿機構模型的建立

兩腿分別使用一套波舍利直線運動機構（Peaucellier-Lipkin linkage），或者霍肯直線運動機構（Hoeckens Linkage）。一腿的兩個端點固定在軀干上，另一腿對稱固定；軌跡為直線的點視為腳（圖4）。

2.連桿機構模型的行走設定及效果

兩腿交替行走，假設重心橫向移動為零，最大步幅是以軌跡為直線的點的極限，步幅可以是極限內的任意長度，不限定每一步幅長度。

在以上設定下，連桿機構模型重心運動軌跡與路面平行，得出連桿機構模型的阻力矩為零，得出連桿機構模型可以無阻力地運動。

3.連桿機構模型推手推車的運動狀況分析

（1）連桿機構模型增設手臂，推手推車時，設為單一剛桿，手掌摩擦力無窮大，單一剛桿可以從任意角度過手推車質心施力；拉手推車時，設為繩，繩可以從任意角度過手推車質心施力；無論推還是拉，連桿機構模型的手臂均具有單一剛桿及繩兩個功能。（2）設手推車質量為m；連桿機構模型質量為M，自由落體加速度為g。對手推車所施的力為F，連桿機構模型腳部靜摩擦力的反作用力為Ffoot，視為腳發力。手推車重力為Fgm，連桿機構模型重力為FgM。（3）對施力角度，建立平面直角坐標系XOY，設O為手推車質心，以X軸正向為0度，計算推車夾角θ。

在以上設的情況下，連桿機構模型推手推車的運動狀況為：

Ffoot=Fcosθ （1.1）

Fcosθ=（M+m）a （1.2）

Ffoot==（M+m）a （1.3）

（1.1）表明腳部發力，與連桿機構模型推力Fcosθ相等。（1.2）表明M及m由連桿機構模型、手推車分別的承擔力為多少，不影響運動狀況；M與m之和作為確定值，共同影響影響運動狀況。（1.3）表明腳部發力Ffoot，決定M+m的加速度a。

所以，發力大小及方向由Ffoot決定，F及θ只是傳導機構，不改變Ffoot發力的大小及方向；Ffoot影響M+m的運動狀況，決定a的大小。

4.連桿機構模型推手推車的省力狀況說明

省力與否，決定于一定的Ffoot之下a的大小。前面已經有結論Ffoot=（M+m）a，一定的Ffoot產生確定的a，二者成正比。F及θ只是傳導機構，不改變Ffoot發力的大小及方向，與省力與否無關。

區分推力角度不同的情況，具體說明如下：

（1）在第一象限，推力指向手推車質心O，與水平面呈一定角度θ（如30度）推車。部分M由手推車承擔。（2）θ順時針轉，直到X軸正向，推力指向手推車質心O，以0度推車。Fcos0=（M+m）a，F=（M+m）a，a與F成正比，F對a的影響達到最大值，最省力。（3）θ逆時針轉，直到90度。相當于坐。（4）θ逆時針轉，過0度，反方向運動。（5）θ順時針轉，過90度，相當于拉。（6）θ順時針轉，過90度，直到180度。相當于扛。（7）θ順時針轉，過180度，反方向運動。（8）θ順時針轉，繼續過180度，直到270度，反方向運動。同90度，但方向相反。（9）θ順時針轉，繼續過270度，與（4）相同。

以上為全方位（角度）360度。

以上推改為拉，二者的結果是一樣的。

俗話說：“背著抱著一般沉。”本文提出，在設定條件下，連桿機構模型拉與推手推車所用力相等，可推出一個匪夷所思的結論：“扛著坐著一般沉。”

實際中，列車在鐵軌上運行，重心起伏較為平緩，機車施力于車輛，拉與推區別不大。

五、初步結論及未盡問題

對第一種情況“拉的方法省力”，本文簡單明確了基于克服摩擦力，形成“拉的方法省力”的結論。對于第二種情況“推的方法省力”，本文分層次提出了重點。首先明確了阻力矩決定手推車運動的力。之后提出是否省力，需要比較手推車與人兩個系統，看哪一個需要克服阻力的力更小。最后列舉極端情況，扛著手推車與坐著手推車作比較。對第三種情況“拉與推所用力相等”，本文作了較為詳細的分析。一方面說明在理想狀態下，手推車可以無阻力地運動。另一方面，分析了人的行走模型，利用波舍利直線運動機構（及霍肯直線運動機構）建立了連桿機構模型，得出在設定條件下，拉與推手推車所用力相等的結論。最后，同樣列舉極端情況，機車在鐵軌上拉與推車輛區別不大。對第四種情況“無法判斷”拉與推哪種方法省力，筆者還不能提出實例，沒有能夠給出結論。

個人能力有限，此研究還有很多需要改進完善之處。如果將此問題展開研究是十分復雜的，例如，動摩擦如何向靜摩擦過渡，以及影響動摩擦與靜摩擦的參數有何關系，并且人所施加的力對它們有何影響，雙足行走模型與現實的差別，加上腳踝后施力方式的改變，等等。

參考文獻：

[1]哈爾濱工業大學理論力學教研室.理論力學[M].7版.北京：高等教育出版社，2009.

[2]李紅征.小型雙足機器人的行走研究[D].中國科學技術大學，2008.

[3]顧森.思考的樂趣[M].北京：人民郵電出版社，2012.