補圖是獨立數為n-2的雙圈圖的最小特征值

蘆興庭，余桂東，嚴亞偉，孫 威

設G是一個n階簡單無向圖，記其頂點集為V={v1,v2,…,vn} ，邊集 E={e1,e2,···,em} 。 NG(v)表示G中與v相鄰的點的集合，且記v的度數d(v)= | NG(v) |。設S?V，圖G[S]表示以S為頂點集，以G中兩端點均在S中的邊為邊集的圖，稱其為G的導出子圖。若圖G[S]中無邊，則稱S為G的獨立集。G中含點數最多的獨立集所含的點數稱為G的獨立數，記為 α(G)。記Gc=(V , Ec)為圖G=(V ,E )的補圖，其中

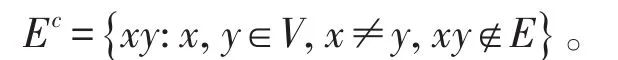
圖G的度矩陣記為 D(G)=diag(d(v1),d(v2),···,d(vn) )，其中d(vi)是頂點vi的度數，i=1,2,…,n。圖G的鄰接矩陣為A(G)=(aij)n×n，如果vivj∈E，則aij=1；否則aij=0。圖G的無符號拉普拉斯矩陣為Q(G)=D(G)+A(G )，因為 A(G)，Q(G)是實對稱矩陣，因此它們的特征值是實數，故可排序。A(G)的最小特征值稱為圖G的最小特征值，不妨設A(G)的n個特征值從大到小排列為 λ1(G ) ≥λ2(G ) ≥…≥λn(G )，最大特征值 λ1(G)稱為圖G的譜半徑，記作λmax(G )；最小特征值λn(G )稱為圖G的最小特征值，記作λ(G )，其對應的特征向量稱作G的第一特征向量。由于Q(G)是半正定的，所以Q(G)的特征值從大到小排列為q1(G ) ≥q2(G )≥···≥qn(G )≥0，其中最大特征值q1(G)稱為圖G的無符號拉普拉斯譜半徑；最小特征值qn(G)稱為圖G的無符號拉普拉斯最小特征值，記作a(G)，其對應的特征向量稱作G的無符號拉普拉斯第一特征向量。

近年來，無符號拉普拉斯最小特征值的問題已經越來越受到重視，其中文獻[1-4]研究了一類圖的極小特征值，文獻[5-10]研究了某一類特殊圖的最小特征值；而文獻[11-15]都是從補圖的結構出發，分別研究了補圖是樹、單圈圖、連通圖、2-點（邊）連通圖的圖的最小特征值，和補圖是樹、單圈圖的無符號拉普拉斯最小特征值。受此啟發，本文研究n階且補圖為獨立數n-2的雙圈圖的最小特征值和最小無符號拉普拉斯特征值，并刻畫了此類圖最小特征值和無符號拉普拉斯最小特征值達極小的圖。 G=(V ,E)為n階簡單圖，對于向量X∈Rn，如果存在一個從V到X中值的映射φ，使得對于任意u∈V有Xu=φ(u)，則稱X定義在G上。

對于任意向量X∈Rn，有

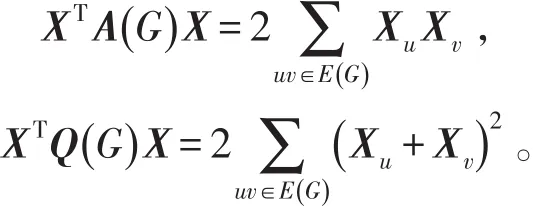
若λ是A(G)對應于特征向量X的特征值，則由特征值的定義，當且僅當X≠0時，對于每個v∈V ，有

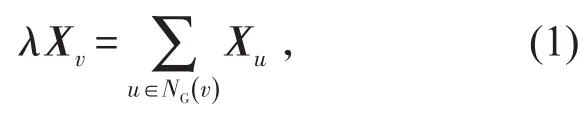
稱（1）式為G關于X的特征等式。另外，對于任意單位向量X∈Rn，有

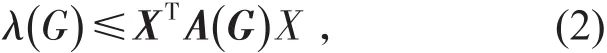
當且僅當X是G的第一特征向量時等號成立。

若q是Q(G)對應于特征向量X的特征值，則由特征值的定義，當且僅當X≠0時，對于每個v∈，有

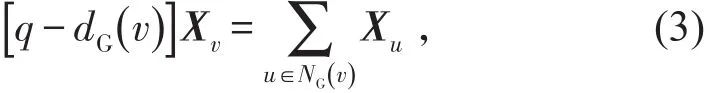
稱(3)式為G關于X的無符號拉普拉斯特征等式。另外，對于任意單位向量X∈Rn，有

當且僅當X是G的無符號拉普拉斯第一特征向量時等號成立。

引理1[15]設G是一個簡單圖，有

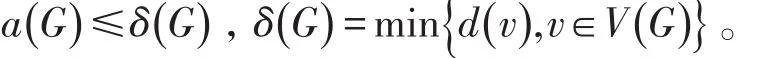
引理2[16]設A是一個實對稱n×n階鄰接矩陣，鄰接矩陣 B為 A的 m×m階主子陣，且μ1(A )≥μ2(A )≥…≥μn(A),μ1(B )≥μ2(B )≥…≥μm(B)分別為A與B的特征值，則對于i=1,2,…,m，有μn-m+i(A )≤μi(B ) ≤μi(A)。

對于獨立數為n-2的雙圈圖，它的雙圈必共邊，其兩內圈為C3，外圈為C4，且兩個內圈的公共點上分別懸掛 p個與q個懸掛點，其中p+q=n-4,p,q≥0，如圖1所示，記為G(p ,q)。

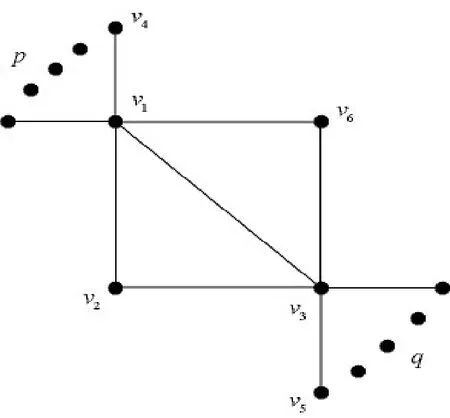
圖1 G(p ,q)

定理1 給定一個正整數n(n≥7)，對于任意的整數 p,q≥0且 p+q=n-4，則有

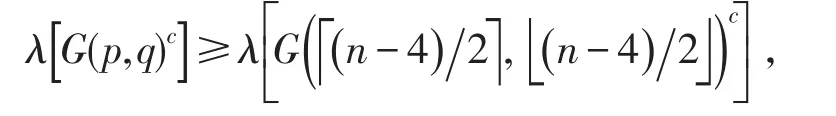
證明 設G(p ,q)如圖1所示，X是G(p ,q)c的第一特征向量。由于K2是2點完全圖，K2?G(p ,q)c，且λ(K2)=-1，根據引理2知≤-1。記X1:=Xv1，X2:=Xv2，X3:=Xv3，X6:=Xv6，根據(1)式知X2=X6；所有懸掛在v1上的點在X中對應的值相同，記作X4，所有懸掛在v3上的點在X中對應的值相同，記作X5，并且記λ:=

（i）若q=0，由（1）式可以得到

將上式轉換成矩陣等式( )B-λI X'=0，其中

令f1(x ;n-4,0)=det(B -xI)，可以得到

則λ為 f1(x ;n-4,0)=0的最小根。

當x=-1.8時，有

當n≥7時，有 f1(- 1.8;p,q) ＜0，從而λ＜-1.8。

（ii）若q≥1，由（1）式可以得到

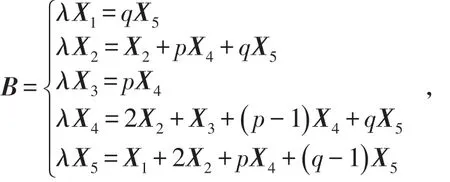
將上式轉換成矩陣等式(B -λI) X′=0， ，其中

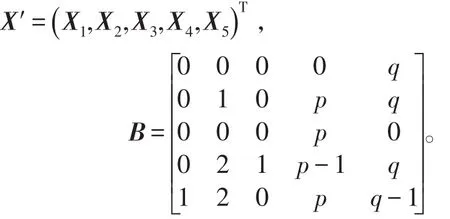
令f2(x;p,q)=det(B -xI)，可以得到

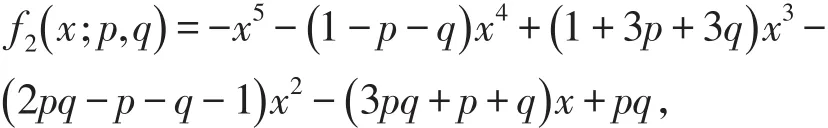
則λ是 f2( )

x;p,q=0的最小根。

當x=-1.8時，有

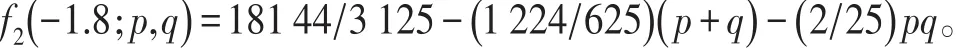
當n≥7時，p+q=n-4≥3，此時f2(- 1.8;p,q) ＜0，從而λ＜-1.8。當 p≥q+2，x＜-1.8時，有

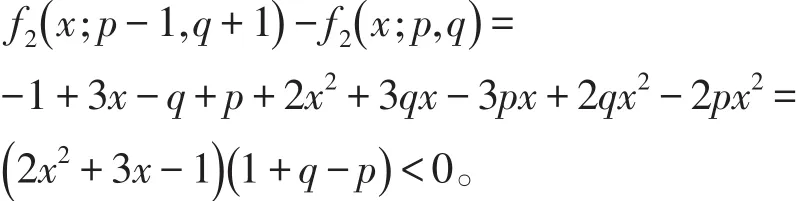
由于λ是方程 f2(x ;p,q)=0的最小根，從而有f2(λ ;p,q)=0，且 λ＜-1.8，由上式可得到f2(λ ;p-1,q+1) ＜0，這意味著

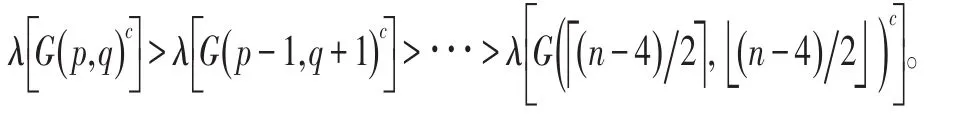
（iii）比較 λ[G ( n -4,0)c]與 λ[G ( n -5,1)c]的大小，設g(x)=f1(x ;n-4,0)(- x-1)=

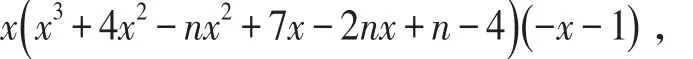
則有g(x)-f2(x ;n-5,1)=(n -5)(2 x2+3x-1)，這樣，當 x＜-1.8，n≥7時，有g(x)-f2(x ;n-5,1) ＞0。由（i）（ii）知，λ[G ( n -4,0)c]＜-1.8，λ[G ( n -5,1)c]＜-1.8，即 λ[G ( n -4,0)c]＞λ[G ( n -5,1)c]，于是根據（i）（ii）（iii）知結論是成立的。

定理2給定一個正整數n(n≥7)，對于任意的整數 p≥q≥1且 p+q=n-4，有

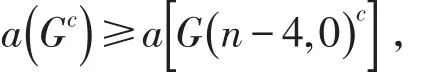
當且僅當G(p ,q)=G(n -4,0)時等號成立。

證明 G(p ,q)如圖1所示，設X是G(p ,q)c的無符號拉普拉斯第一特征向量。由引理1知， 記 X1:=Xv， X2:=，

1X3:=Xv3，X6:=Xv6，根據(3)式知 X2=X6；所有懸掛在v1上的點在X中對應的值相同，記作X4，所有懸掛在v3上的點在X中對應的值相同，記作X5；并且記

由(3)式可以得到

將上式轉換成矩陣等式( )kI-B X'=0，其中

令f3(x ;p,q)=det(x I-B )，可以得到

則k是 f3(x ;p,q)=0的最小根。

當 p≥q≥1時 ，有 f3(x ;p+1,q-1)-f3(x ;p,q)=(1 +p-q)(p +q-x)(x2-3qx-3px+2q2+4pq+2p+2q+2p2)。令

則有g'(x)=2x-3p-3q。

當0＜x≤q時，觀察到 g'(x)是遞增的，且有g'(x)≤g'(q)=-3p-q＜0，故此時 g(x)在0＜x≤q上單調遞減，即有g(x)≥g(q)=pq+2q+2p+2p2＞0。

進一步有

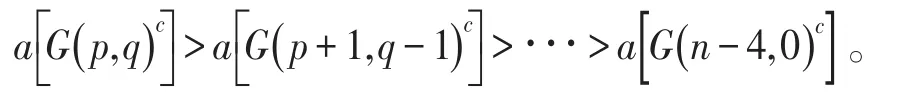
參考文獻：

[1]BELL F K,CVETKOVIC D,ROWLINSON P,et al.Graph for which the least eigenvalues is minimal,I[J].Linear Algebra Appl,2008,429(8)：234-241.

[2]BELL F K,CVETKOVIC D,ROWLINSON P,et al.Graph for which the least eigenvalues is minimal,II[J].Linear Algebra Appl,2008,429(8)：2168-2176.

[3]CARDOSO D M,CVETKOVIC D,ROWLINSON P,et al.A sharp lower bound for the least eigenvalue of the signless Laplacian of a non-bipartite graph[J].Linear Algebra Appl,2008,429(11-12)：2770-2780.

[4]FAN Y Z,WANG Y,GAO Y B.Minimizing the least eigenvalues of unicyclic graphs with application to spectral spread[J].LinearAlgebraAppl,2008,429(2-3)：577-588.

[5]LIU R,ZHAI M,SHU J.The least eigenvalues of unicyclic graph with n vertices and k pendant vertices[J].Linear Algebra Appl,2009,431(5-7)：657-665.

[6]PETROVIC M,BOROVICANINB,ALEKSIC T.Bicyclic graphs for which the least eigenvalue is minimum[J].Linear AlgebraAppl,2009,430(4)：1328-1335.

[7]TANY Y,FAN Y Z.The vertex(edge)independence number,vertex(edge)cover number and the least eigenvalue of a graph[J].LinearAlgebraAppl,2010,433(2)：790-795.

[8]WANG Y,FAN Y Z.The least eigenvalue of a graph with cut vertices[J].LinearAlgebraAppl,2010,433(1)：19-27.

[9]YE M L,FAN Y Z,LIANG D.The least eigenvalue of graphs with given connectivity[J].Linear Algebra Appl,2009,430(4)：1375-1379.

[10]YU G D,FAN Y Z,WANG Y.Quadratic forms on graphs with application to minimizing the least eigenvalue of signless Laplacian over bicyclic graphs[J].Electronic Journal of Linear Algebra,2014,27(1081-3801)：213-236.

[11]FAN Y Z,ZHANG F F,WANG Y.The least eigenvalue of the complements of tree[J].Linear Algebra Appl,2011,435(7)：2150-2155.

[12]WANG Y,FAN Y Z,LI X X,et al.The least eigenvalue of graphs whose complements are unicyclic[J].Discussiones Mathematicae Graph Theory,2013,35(2)：1375-1379.

[13]YU G D,FAN Y Z.The least eigenvalue of graphs[J].Math Res Expo,2012,32(6)：659-665.

[14]YU G D,FAN Y Z.The least eigenvalue of graphs whose complements are 2-vertex or 2-edge connected[J].Operations Research Transactions,2013,17(2)：81-88.

[15]LI S C，WANG S J.The least eigenvalue of the signless Laplacian of the complements of trees[J].Linear Algebra Appl,2012,436(7)：2398-2405.

[16]HAEMERS W.Interlacing eigenvalues and graphs[J].Linear AlgebraAppl,1995,226-228：593-616.