基于極端學習機算法的蟲情預測研究

趙 健

（中國電子科技集團公司電子科學研究院，北京100041）

1 引言

近些年，社會經濟的快速發展給環境造成了不可忽視的負面影響，使得環境日益惡化，也給農業生產帶來了一些嚴重問題。農業方面比較突出的問題就是病蟲害，所以根據農作物的生長環境、氣候的變化規律、病蟲害發生的條件等方面的相關資料[1]，對病蟲害的產生進行全面的研究，做出相應的蟲害預測并對農戶作出指引，有很重要的社會意義[2-3]。蟲害與地震、海嘯一類的天災不同，對于農作物蟲害的研究和預測是以先期獲得的數據資料為基礎進行的，具有一定的可預測性。高準確地預測出蟲害的發生，能為綜合治理工作打下堅實的基礎。

由于蟲情問題對社會生產生活的重要影響力，對蟲情預測的研究由來已久。先期提出的蟲情預測方法有：觀察法、統計法、數學生態模型法。這些方法在具體應用情況下有極大的局限性，包括：訓練過程的收斂速度較慢，降低實時信息的獲取效率；對于測試蟲情樣本的預測正確率不高等。專家系統的使用具有一定的局限性，適用性不佳。現有的蟲情預測研究并不能滿足農業經濟生產工作的實際需要。對蟲情預測需要進行更深入的探討，來提高蟲情預測的科學性、準確性，更好地為農業經濟的發展提供保障。蟲情預測的樣本具有不確定性，在使用預測方法對其蟲害級別作出評估時，結果容易陷入局部最小而發生不收斂，最終得出的結果精度相對較低；相比之下，極端學習機（Extreme Learning Machine,ELM）算法沒有前者的局限性，可以從本質上解決蟲情預測準確率低的問題。本研究即引入極端學習機算法進行蟲情預測研究工作。

2 極端學習機算法研究

如圖1所示即為ELM算法的結構原理圖。圖中包括了三個層次：輸入層、輸出層、隱含層[4]。

圖1 ELM算法的結構

假設激活函數g無限可微，則可得到ELM訓練設定的隱層數遠小于樣本的觀測數，即L≤N，以此為基礎，可得到以下兩個與ELM算法密切相關的定理:

(1)定理1

對這一定理的證明過程如下：

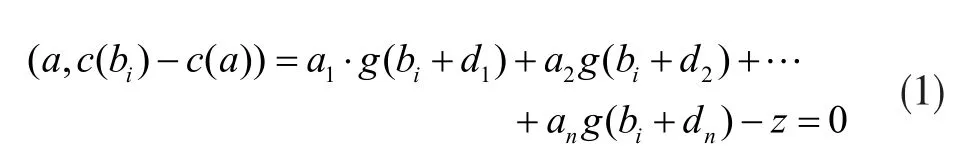
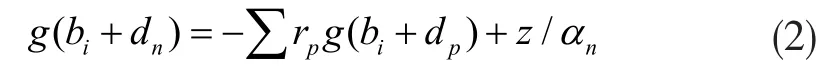
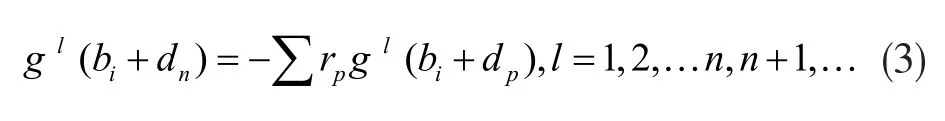
式中，g(l)為函數g對bi的l階導。但是，在N-1個自由系數r1,...,rn-1的情況下，其線性方程卻多余N-1個，他們之間有矛盾沖突了。所以可得c不屬于維度比N小的子空間。

因此，在(a,b)有一定概率能夠隨機選N個隱含節點對應的N個偏置值b1,...,bn-1，滿足其對應的c(b1),c(b2),...,c(bn)能夠跨度表明對于所有的可以按照所有連續概率從的所有區間進行選擇，滿足H是滿秩的列向量。

其中，激活函數有：Sigmoid、徑向基函數、正弦函數、余弦函數、指數函數還有別的非正則函數[6]。

普通的單層神經網絡的相關參數需要進行調整，相比之下定理1有所不同，它證明了從經驗上來說是不需要經過調整的，通過剛開始的參數設定后，ELM的系數矩陣H在算法運行過程中是保持不變的。所以說，對于一定的，根據式(2)可知，單隱層神經網絡算法的求解過程，都可轉化為的求解過程：

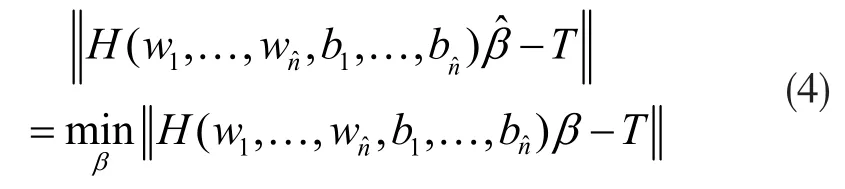
式中H+為H的MP偽逆。

(2)定理2

如果有矩陣G滿足：Gy為線性方程Ax=y的一個最小二乘解。則有G=A+。A+即A的MP偽逆[7-10]。

根據定理2，可以將極端學習機算法的重要屬性歸納如下:

(a)特別地，x0=A+y與Ax=y的最小二乘解為:

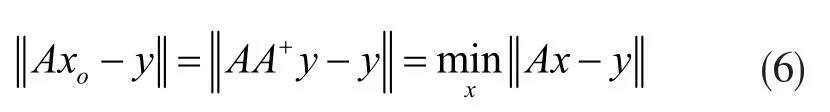
(b)接下來，x0=A+y在Ax=y的所有最小二乘解里具有最小的模:

(c)Ax=y的具有僅有的最小模最小二乘解 x=A+y。

基于以上的定理，可歸納出ELM的學習規則如下:

(b)隱層輸出矩陣H的獲得;

其中H+為H的MP偽逆，

農村生態建設工作是我國現代化建設的重要內容之一。農村生態建設工作的目的，在于提高農村居民生活環境，推動農村地域經濟發展，助力我國經濟的可持續發展。不過就實際而言，目前我國村鎮規劃與建設工作尚有許多問題未能有效解決。

計算H的MP偽逆的方法有很多，包括：正交投影法，正交法，迭代法，奇異值分解法(SVD)等。為了在極端學習機算法中減少搜索與迭代的次數。正交投影方法在HTH是非奇異時使用但是，HTH不可能一定已知非奇異，某些情況下是奇異的，所以正交投影方法沒有獲得理想的效果。SVD是用來獲取H的MP偽逆的一種常用方法。

3 基于極端學習機算法的蟲情預測研究

對采用極端學習算法實現蟲情的預測，具體可分為以下幾步：

(1)獲取蟲情數據，預處理

蟲害的發生與自然因素有一定的相關性，會受到氣溫、日照、降雨等因素的影響。在研究過程中主要應考慮這樣的因素變量。本研究訓練樣本使用的數據為某林區從1996年到2013年的總計18年間的蟲情樣本數據。為了使得預測算法對于蟲情樣本有更好的擬合度，對訓練樣本加入高斯白噪聲后產生測試樣本數據，對18年時間里的總共108組數據進行測試。

(2)極端學習機預測模型構建

由于蟲情預測樣本的數量是一定的，所以測試樣本只能通過加入高斯白噪聲獲得，試用語句

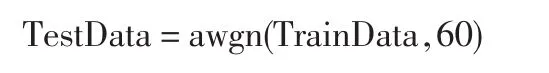
其中的TestData即為測試數據。

其中“radbas”為激活函數，1表示使用ELM算法進行分類（包括二分類和多分類）。仿真結果如圖2。

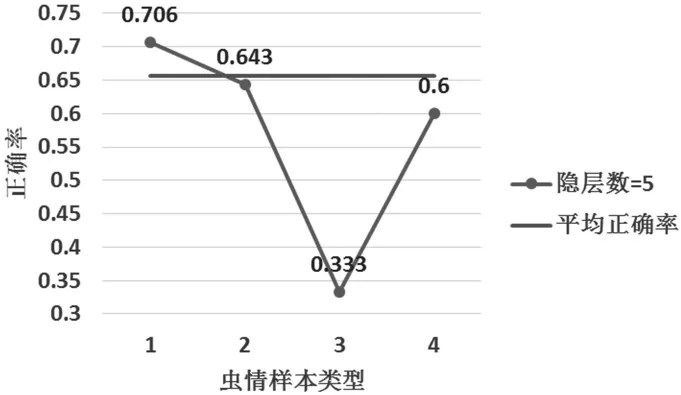
圖2 隱層數=5時的蟲情樣本預測情況

(3)蟲情預測算法效果對比

作為對比，在極端學習機算法之外，再采用常用的BP神經網絡、SVM支持向量機、決策樹算法來執行同一項蟲情預測。這四者的對比結果如表1所示。

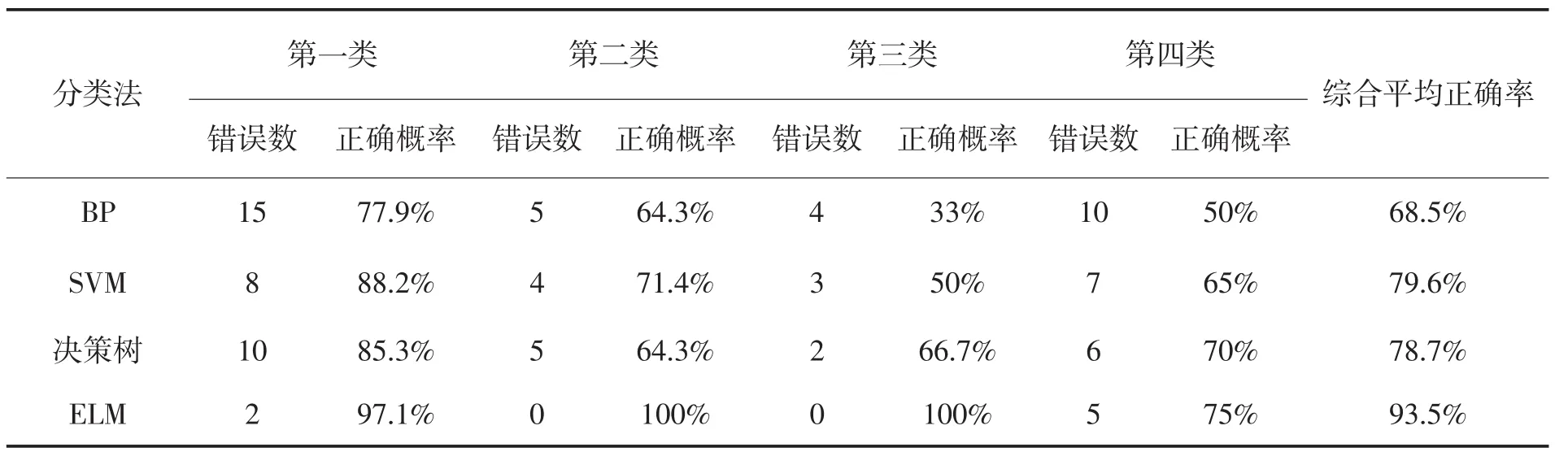
表1 蟲情預測算法的結果對比

從表中的結果對比來看，基于ELM的蟲情預測算法實現了對四類蟲情級別精準與快速預測，其效果明顯優于經典的分類算法神經網絡、SVM和決策樹算法；分類正確率均勻分布，每類蟲情級別都獲得了較高的正確率，預測能力較強。

從對比的結果中可以歸納出以下結論：

(1)極端學習機算法對蟲情樣本的預測效果最好，其次是SVM支持向量機和決策樹，BP神經網絡的效果最差。極端學習算法在蟲情樣本預測的有效性方面較為優越。

(2)基于極端學習的蟲情預測模型有較強的適用性，蟲情樣本具有復雜性與不確定性，如上構建的模型也適用于其他農作物蟲害等級的預測。

4 結束語

本文詳細分析極端學習機算法的原理機制，這些都是研究蟲情預測技術的基礎理論。之后介紹了農作物蟲害相關因素，主要包括：溫度、日照、降雨，對這幾個因素進行綜合考慮構建蟲情樣本特征矩陣后，使用極端學習機算法、高斯混合模型算法進行蟲害等級的預測，通過實驗仿真結果，對比了與常用算法的實驗效果，驗證了這種算法對于蟲情樣本的預測具有可行性，預測的正確率較高，對農作物所遭受的蟲害程度做出了高精度的判定，能夠為蟲害的防治工作提供依據，減少蟲害，該方法優于傳統的蟲情預測研究方法，具有很高的實用價值。

[1]QIN J L,YANG X H,YANG Z W,et al.New technology of using meteorological information in forest insect pest forecast and warning systems[J].Pest Management Science,2017.

[2]QIN J,FU H,YANG X,et al.Innovative design and its application on the meteorology serving system for pest forecast and warning[J].Journal of Meteorological Research&Application,2017.

[3]LIU W.Research progress on modern tools for crop pests forecasting in China[J].China Plant Protection,2017.

[4]張博洋,李素梅.應用深度極限學習機的立體圖像質量評價方法[J].小型微型計算機系統,2017,38(11):2586-2590.ZHANG Boyang,LI Sumei.Stereoscopic image quality assessment method using deep extreme learning machine[J].Journal of Chinese Computer Systems,2017,38(11):2586-2590.

[5]高鑫,歐陽寧,袁華.基于快速去噪和深度信念網絡的高光譜圖像分類方法[J].桂林電子科技大學學報,2016,36(6):469-476.GAO Xin,OUYANG Ning,YUAN Hua.A hyperspectral image classification method based on fast denoising and deep belief network[J].Journal of Guilin University of Electronic Technology,2016,36(6):469-476.

[6]臧維明,華驊,賴炳宇,等.一種跨平臺敏捷式動態可重構系統架構研究[J].中國電子科學研究院學報,2017,12(3):225-231.ZANG Weiming,HUA Hua,LAI Bingyu,et al.Research on c oss-platform agile dynamic reconfigurable system architecture[J].Journal of China Academy of Electronics and Information Technology,2017,12(3):225-231.

[7]BARNICH O,DROOGENBROECK M V.ViBe:A universal back-ground subtraction algorithm for video sequences[J].IEEE Transactions on Image Processing,2011,20(6):1709-1724.

[8]DANG U J,Punzo A,McNicholas P D,et al.Multivariate response and Parsimony for Gaussian Cluster-weighted models[J].Journal of Classification,2017,34(1):1-31.

[9]BRIF C,MANN A.A hybrid intelligent approach for the prediction of electricity consumption[J].International Journal of Electrical Power&Energy Systems,2012,43(1):99-108.

[10]DING S,ZHAO H,ZHANG Y,et al.Extreme learning machine:algorithm,theory and applications[J].Artificia Intelligence Review,2015,44(1):103-115.

[11]任露,黃穎為.基于牛頓迭代法的分形圖像研究[J].西安理工大學學報,2016,32(2):247-252.REN Lu,HUANG Yingwei.Fractal image research based on Newton iteration[J].Journal of Xi'an University of Technology,2016,32(2):247-252.

[12]明艷.基于3D相鄰區域宏塊相關性的多視點視頻快速編碼算法[J].重慶郵電大學學報(自然科學版),2016,28(6):783-788.MING Yan.Fast multi-viewpoint video coding algorithm based on 3D adjacent area macroblock correlation[J].Journal of Chongqing University of Posts and Telecommunications(NaturalScience),2016,28(6):783-788.