基于粒子群投影尋蹤插值模型的土壤質量評價

, ,

(新疆大學 信息科學與工程學院， 新疆 烏魯木齊 830046)

1 材料與方法

1.1 評價等級標準的建立方法

土壤質量評價的框架體系要確保全面性。影響土壤質量的因素很多，選取的指標應能正確反映土壤基本功能，又能避免使指標體系過于復雜化[2]。土壤質量評價體系目前沒有明確標準，根據全國第2次土壤普查質量評價指標體系，本文中選取8個代表性的分析性定量指標，即有機質、全氮、全磷、全鉀、速效氮、速效磷、速效鉀、pH。各個因素的指標評價標準如表1所示。

1.2 建立模型

針對非線性、 非正態高維觀測數據(生物學指標、 化學指標等)難以計算處理的情況，采用投影尋蹤(projection pursuit)方法將數據投影到低維子空間對投影值進行統計分析，獲得高維數據的結構特征[7-8]。在土壤數據的分析過程中，確定最佳投影方向是解決評價問題的關鍵點，傳統的優化方法對于計算特定目標函數具有一定的優勢，本文中構建的投影尋蹤插值模型基于粒子群算法[9]，可以有效地克服傳統方法的局限性，具體步驟如下。

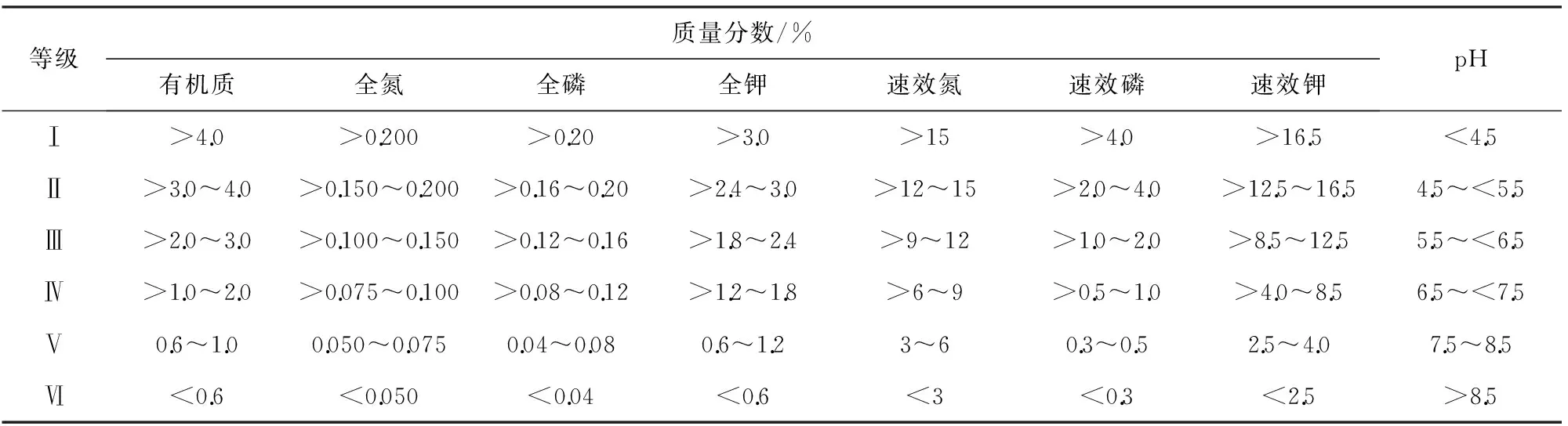
表1 土壤質量等級評價標準

1.2.1 建立樣本集

設由評價標準表產生的樣本經驗等級為y(i)，樣本指標表示為{x*(i,j)|i=1, 2, …,n;j=1, 2, …,p}，其中n為樣本個數，p為指標個數，1～N表示等級由低到高。先對各指標值無量綱化處理，統一變化范圍，加快訓練的收斂性，然后進行歸一化處理。

對于正向指標，

(1)

對于逆向指標，

(2)

式中：xmax(j)、xmin(j)表示第j個指標值的2個極值；x(i,j)為指標特征值歸一化的序列[10]。

式(1)、(2)應用于正向指標(權重大于0)和逆向指標(權重小于0)的歸一化處理，但對于不能明確判定指標特征的，則采用式(1)進行歸一化處理。

1.2.2 投影值的計算

設a=(a1,a2, …,ap)為投影方向， 將數據x(i,j)投影到a上，得到投影值z(i)，

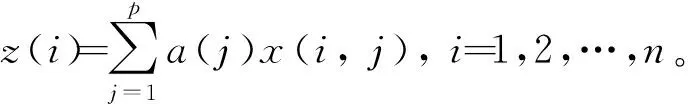
(3)

由式(3)可見，選定最優投影方向后，z(i)的值越大，數據{x(i,j)}中的信息提取得越多。

1.2.3 構造投影指標函數Q(a)

構造投影指標函數

Q(a)=Sz|Rzy|，

(4)

式中：Sz為投影值z(i)的標準差；Rzy為z(i)與y(i)的相關系數。

(5)

(6)

式中E(z)、E(y)分別為序列{z(i)}和{y(i)}的均值。

式(5)中Sz越大，獲得{x(i,j)}的變異信息越多；式(6)中|Rzy|越大，投影值就可以反映預測因子系統更多的變異信息，對預測對象y(i)的解釋性越好。

數據結構的不同特征可以通過不同的投影方向反映，能夠表現出高維數據某類特征結構的就是最佳投影方向，最佳投影方向預測就是投影指標函數的最大化問題[11]，即

maxQ(a)=Sz|Rzy|，

(7)

(8)

a=(a1,a2,…,ap)為優化變量的非線性優化問題，本文中采用罰函數法[12]生成新的目標函數，將有約束優化問題轉化為無約束優化問題，即

(9)

式中h為懲罰因子。

1.2.4 投影指標函數優化算法

粒子群算法通過不斷迭代計算，將每個粒子與其個體歷史最優位置和在粒子群中的全局最優位置比較，從而不斷調整自身位置來接近最優位置，所有粒子的最終聚集位置就是優化問題的解。

投影尋蹤模型中的投影方向即為粒子群算法要優化的問題[13]。設粒子的種群規模為N，第k(k=1,2,…,N)個粒子的速度和位置更新公式為

vk(t+1)=wvk(t)+c1r[qk(t)-ak(t)]+

c2r[g(t)-ak(t)]，

(10)

ak(t+1)=ak(t)+vk(t+1)，

(11)

式中：w為慣性權重因子；c1、c2為常數，稱為學習因子；r是介于[0,1]隨機數；q是歷史最優位置;g是全局最優位置，迭代次數達到預定值，就可通過粒子聚集的位置獲得最佳投影方向a*。

1.2.5 投影尋蹤插值模型

將計算出的最佳投影方向a*代入式(3)獲得投影值z*(i)，根據z*(i)-y(i)的散點圖建立土壤等級評價模型y*=f(z)，代入歸一化處理后的評價樣本得出各評價樣本的所屬等級。

2 結果與分析

選取全國第2次土壤普查中的黑龍江省、長白山、內蒙古自治區及新疆維吾爾自治區阜康市共4個地區剖面取樣的4組實測數據作為待評價的樣本，見表2。

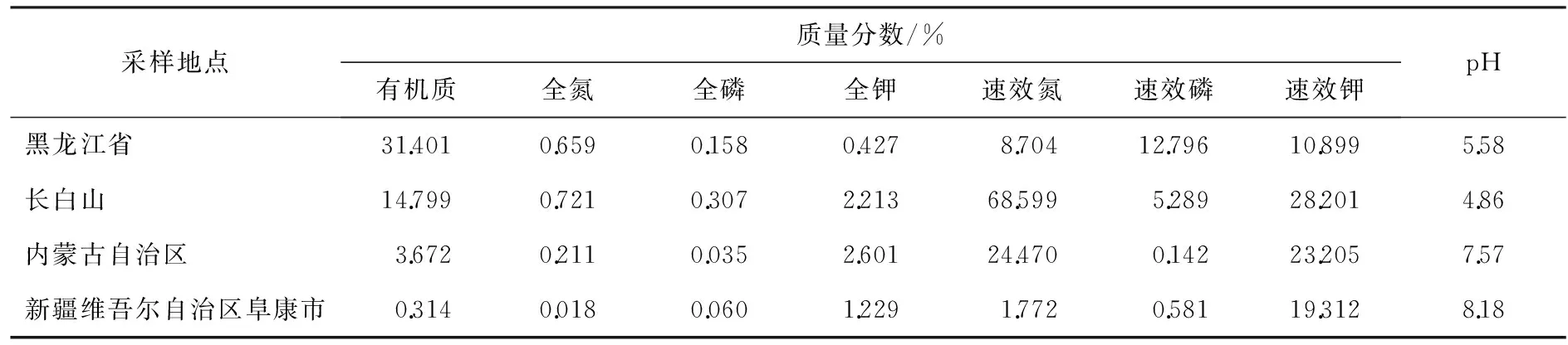
表2 待評測樣本數據表

按照表1所示的6個土壤質量評價等級范圍，從全國第2次土壤普查數據中每個等級均勻隨機產生100個指標， 形成600個樣本數據x*(i,j), 并對x*(i,j)進行歸一化處理為x(i,j)，i=1, 2,…,600，y=1,2,…,8。參數設置為：N=100，c1=c2=2，h=200。 MATLAB程序計算出最大投影指標值為0.729 7， 最佳投影方向a*=(0.230 9， 0.211 3， 0.312 1， 0.278 0， 0.431 3， 0.500 2， 0.446 3， 0.305 8)，具體結果見圖1。

最佳投影方向各分量絕對值越大，對質量評價影響就越大，該數據還可以作為檢驗土壤質量分級標準合理性的依據。將a*代入式(3)可以計算出最佳投影值，最佳投影值與對應等級如圖2所示。

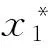
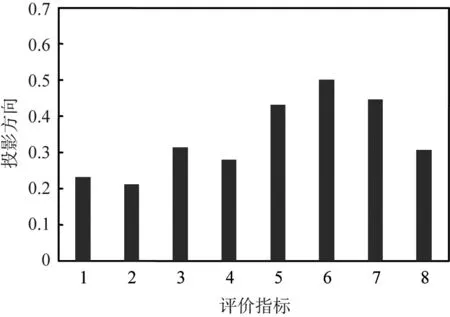
圖1 最佳投影方向a*

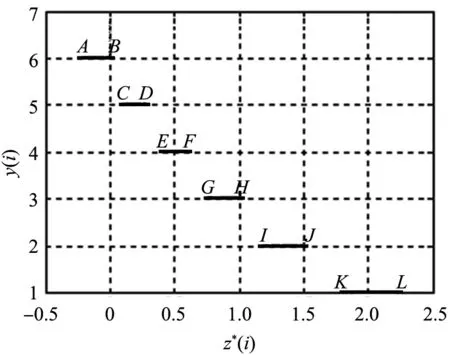
圖2 z*(i)與y(i)的散點關系圖

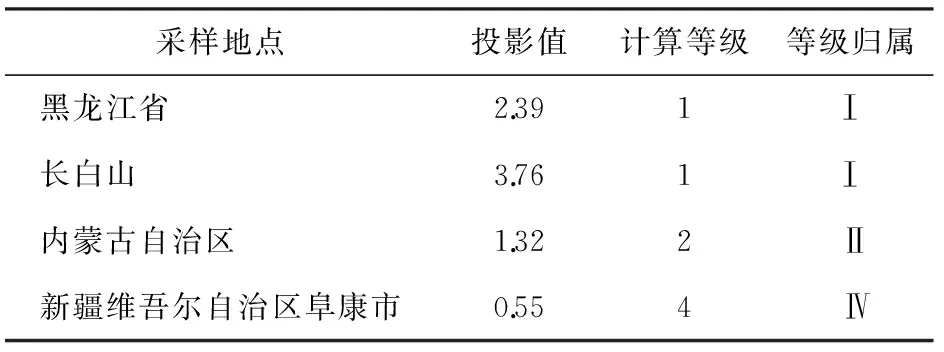
表3 土壤質量等級評價結果

3 結論

本文中依據全國第2次土壤普查質量評價等級標準構建評價指標樣本，把樣本數據應用于粒子群投影尋蹤插值模型中，獲得多維土壤質量評價指標的最佳投影值， 根據最佳投影值與質量等級的對應關系建立插值模型以實現對土壤質量等級的綜合評價。模型建立和評價的方法切實可行，評價結果科學合理，避免了人為干擾，為土壤質量評價等方面的研究提供了一個新思路。

參考文獻:

[1] 路鵬, 蘇以榮, 牛錚, 等. 土壤質量評價指標及其時空變異[J]. 中國生態農業學報, 2007, 15(4):190-194.

[2] 黃勇, 楊忠芳. 土壤質量評價國外研究進展[J]. 地質通報, 2009, 28(1): 130-136.

[3] 吳玉紅, 李云，郝興順，等. 土壤質量評價國內外研究進展[J]. 安徽農學通報, 2012, 18(16):24-25.

[4] 黃鑫,李洪良,邱林. 土壤質量等級模糊模式識別綜合評價研究[J]. 人民黃河，2012，34(3):68-70.

[5] 劉占鋒, 傅伯杰, 劉國華, 等. 土壤質量與土壤質量指標及其評價[J]. 生態學報, 2013, 26(3): 901-913.

[6] 張鑫, 余樹全, 李清林, 等. 洞頭列島土地利用對土壤及沉積物重金屬污染的影響及其生態風險評價[J]. 生態科學, 2016, 35(5):126-135.

[7] ZHANG H L, WANG C, FAN W H. A projection pursuit dynamic cluster model based on a memetic algorithm[J]. Tsinghua Science and Technology, 2015, 20(6): 661-671.

[8] 韓銳, 董增川, 施露, 等. 投影尋蹤法在灤河流域生態系統健康評價中的應用[J]. 水力發電，2016，42(9):5-8.

[9] LIU Y L, LIU D F, LIU Y F, et al. Rural land use spatial allocation in the semiarid loess hilly area in China: using a particle swarm optimization model equipped with multi-objective optimization techniques[J]. Science China Earth Sciences, 2012, 55(7): 1166-1177.

[10] 陳默. 基于投影尋蹤等級評價模型的大伙房水庫水質評價[J]. 甘肅水利水電技術, 2016, 52(12):1-3.

[11] 李芳鳳, 張國權. 粒子群投影尋蹤模型在土壤重金屬監測中的應用[J]. 廣東農業科學, 2012, 39(8):68-70.

[12] 李志剛, 吳文傳, 張伯明, 等. 一種基于高斯罰函數的大規模無功優化離散變量處理方法[J]. 中國電機工程學報, 2013, 33(4): 68-76

[13] 趙小勇, 付強, 邢貞相. 投影尋蹤等級評價模型在土壤質量變化綜合評價中的應用[J]. 土壤學報，2007，44(1)：164-168.