多重代價多粒度決策粗糙集模型研究*

陳家俊，徐華麗，魏 赟

1.皖西學院 電子與信息工程學院，安徽 六安 237012

2.同濟大學 電子與信息工程學院，上海 201804

3.嵌入式系統與服務計算教育部重點實驗室（同濟大學），上海 201804

4.蘭州交通大學 鐵道技術學院，蘭州 730000

1 引言

粗糙集理論[1-2]是波蘭數學家Pawlak提出的一種處理不確定、不精確信息系統的新型數學工具，決策粗糙集模型[3]是針對經典粗糙集模型在處理分類決策時缺乏容錯能力和風險代價敏感性等問題提出的一種概率型粗糙集拓展模型，是粗糙集理論的重要組成部分，近年來備受廣大學者關注。

對決策粗糙集的研究主要體現在兩方面：一方面為決策粗糙集模型及其拓展模型的研究，如基于風險代價的決策粗糙集模型[4-6]、多用戶決策粗糙集模型[7]、三支決策和決策粗糙集融合模型[8]等。在決策粗糙集模型研究中，閾值的確定問題是其關鍵因素之一，其中基于代價損失的閾值求解方法得到廣泛關注。姚一豫等人[3,9]根據貝葉斯最小風險決策理論，詳細分析了基于代價損失函數的閾值求解方法。決策粗糙集模型是基于單個代價損失矩陣構建的，因此獲得的決策規則及決策代價存在局限性；文獻[4-6]從多代價損失角度出發，提出了多代價決策粗糙集概念，并研究了悲觀決策粗糙集和樂觀決策粗糙集模型。而實際生活中專家給定的代價損失矩陣主觀性較強，且每個專家在領域的認可度差別較大，通過研究樂觀和悲觀代價決策粗糙集模型僅能預測最小和最大決策代價，不能滿足人們往往更希望獲得具有代表性的決策代價的需求。對決策粗糙集的另一研究主要體現在決策粗糙集的屬性約簡、決策分類和規則獲取方法方面，其中決策粗糙集模型的相關性質和屬性約簡算法是重要的研究內容。文獻[10-14]分別從不同的角度研究了決策粗糙集屬性約簡方法。以上無論對決策粗糙集模型還是對決策粗糙集知識獲取方法的研究，都是建立在單一不可分辨關系基礎上，而在實際決策問題分析中，往往需要從多粒度、多層次角度對目標概念進行分析和處理。Qian等人[15]首先將多粒度概念融入到粗糙集模型中，提出了多粒度粗糙集模型，在此基礎上，學者們紛紛提出了各種基于多粒度粗糙集模型的擴展模型和相關算法[16-20]。而現有的多粒度粗糙集模型大都集中在以經典粗糙集和變精度粗糙集模型為基礎的，對于多粒度決策粗糙集模型的研究較少。自2014年Qian等人[21]首先提出多粒度決策粗糙集模型基本框架以來，近兩年對多粒度決策粗糙集模型的研究屈指可數[22-25]，其中文獻[22]分析了不完備多粒度決策粗糙集模型，文獻[24]提出了基于覆蓋的多粒度決策粗糙集模型。而這些文獻僅針對多粒度決策粗糙集模型的構建以及模型所具有的相關性質進行研究，對多粒度決策粗糙集模型中決策代價和多粒度在決策粗糙集模型中的應用并沒有進行深入的研究。

本文在對基于多重代價決策粗糙集模型和多粒度粗糙集模型的研究基礎上，為克服基于單代價損失矩陣構建的模型存在的局限性，綜合考慮多重代價矩陣和多粒度思想，將權重均值代價策略引入決策粗糙集中，提出了一種權重多重代價的不完備多粒度決策粗糙集模型。在不完備信息系統中，分析了悲觀代價決策粗糙集、樂觀代價決策粗糙集和權重多重代價多粒度決策粗糙集模型，并給出了各決策代價的總代價計算公式。最后以權重多重代價的多粒度決策粗糙集模型為例，討論了該模型下隨著粒度的變化其正域的變化情況，并給出了一種基于代價最小化的粒度約簡方法。

2 預備知識

2.1 不完備信息系統與容差關系

若四元組S=(U,A,V,f)是一個信息系統，S包含一組非空的有限對象集合，U={x1,x2,…,xn}為論域；A=C∪D(C∩D=?)表示屬性的有限集合，C表示條件屬性集合，D表示決策屬性集合；，其中Va表示屬性a的值域；F為U×A→V的一個信息函數，表示為f(x,α)∈Va,?α∈A,x∈U；假設C包含m個條件屬性，用C={c1,c2,…,cm}表示，若存在任意ci∈C，x∈U，有f(x,ci)=*（*表示未知屬性值），則稱該信息系統為不完備決策信息系統。

若決策表S=(U,C∪D,V,f)為一個不完備決策信息系統，對于任意子集P?C，由P決定的U上的容差關系TP定義為TP={(x,y)∈U×U|?a∈P,f(x,a)=f(y,a)?f(x,a)=*?f(y,a)=*}。顯然TP滿足自反性和對稱性，而不一定滿足傳遞性。對于?x∈U,TP(x)={y∈U|(x,y)∈TP}稱為x的P容差類，TP(x)描述了與對象x在屬性集合P下的最大不可區分對象子集。對于任意子集X?U，則在屬性集P下X關于容差關系的下近似集和上近似集分別定義為:

2.2 決策粗糙集

若S=(U,C∪D,V,f)為一個不完備決策信息系統，假設Ω={θ1,θ2,…,θm}表示對象的m個狀態集，B={b1,b2,…,bt}表示t個可能的決策，對于任意x∈U，令Pr(θj|x)表示對象x具有狀態θj的條件概率，λ(bi|x)表示對象x在狀態θj下采取決策bi的風險代價，則根據貝葉斯風險決策規則，對象x采取決策bi的期望風險可表示為：

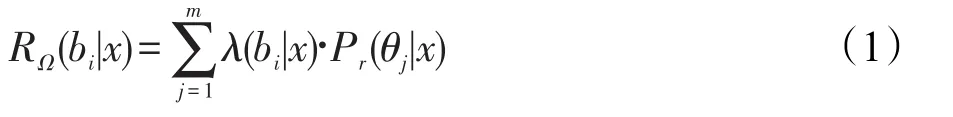
根據Yao提出的決策理論粗糙集，設Ω={X,XL}表示對象的兩種狀態集，每種狀態對應3種決策動作，記為B={αP,αN,αB}，其中αP、αN、αB分別表示將對象x進行分類決策的3種動作行為，即確定將對象x分類到其正域中x∈POS(X)，分類到其負域x∈NEG(X)和分類到其邊界域x∈BND(X)中。當已知一個對象x屬于某個狀態時，采取不同的動作決策就會產生不同的損失。假設決策誤判代價矩陣已由領域專家給出，如表1所示。

Table 1 Misclassification cost matrix表1 決策誤判代價矩陣

依據貝葉斯決策理論和決策誤判代價矩陣，已知對象x(x∈U)，P?C，TP(x)為對象x的P容差類，則對象x采取3種決策產生的期望損失可表示為：

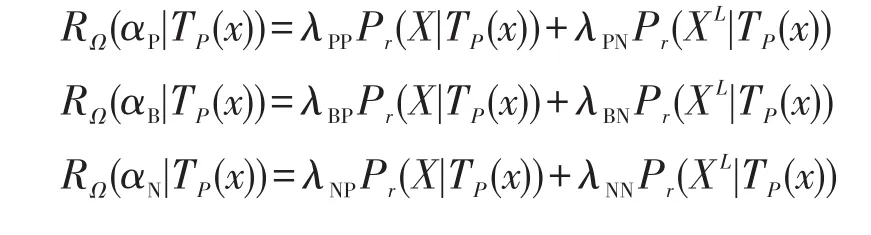
其中，Pr(X|TP(x))和Pr(XL|TP(x))分別表示對象x屬于X和不屬于X的條件概率。

考慮實際應用的合理情況，對于原本屬于X的對象，將其分類到X的正域，其損失小于等于將其分類到邊界域的損失，且兩者的損失均小于將其劃分到負域的損失；反之亦然。即損失函數滿足：λPP≤λBP＜λNP，λNN≤λBN＜λPN。

根據Yao三支決策語義規則可知1≥α≥β≥0。對于給定的不完備決策信息系統S=(U,C∪D,V,f)，由決策屬性D導出的劃分πD={D1,D2,…,Dm}，對?x∈U，則容差決策粗糙集模型下(α,β)- 正區域、邊界域和負區域的決策規則可分別表示如下：

其中Pr(Dmax(TP(x))|TP(x))=表示對象被劃分到具有最大概率的決策類。

2.3 多粒度粗糙集

定義1給定一個不完備決策信息系統S=(U,

C∪D,V,f)，令A1,A2,…,Am為條件屬性C的m個屬性子集，其誘導的容差關系簇為{TA1,TA2,…,TAm}，對于

?X?U，則X關于屬性子集A1,A2,…,Am的樂觀多粒度粗糙集的下、上近似集可分別定義為：

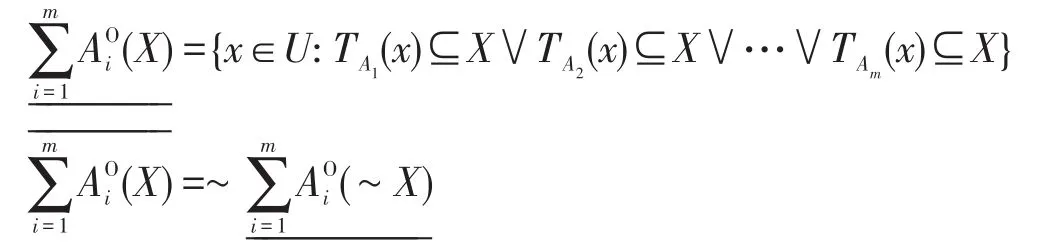
其中～X為X的補集。二元組稱為集合X的樂觀多粒度粗糙集。

定義2給定一個不完備決策信息系統S=(U,C∪D,V,f)，令A1,A2,…,Am為條件屬性C的m個屬性子集，其誘導的容差關系簇為{TA1,TA2,…,TAm}，對于?X?U，則X關于屬性子集A1,A2,…,Am的悲觀多粒度粗糙集的下、上近似集可分別定義為：

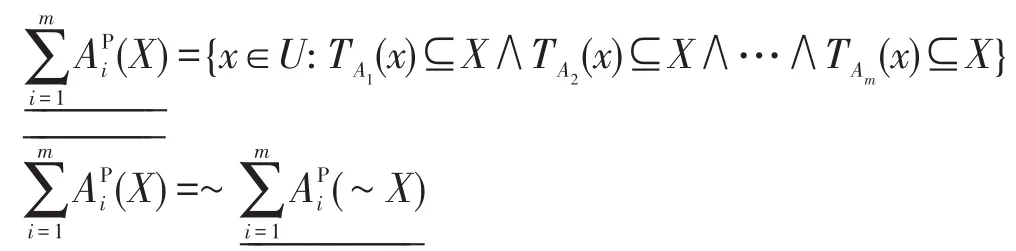
3 多重代價決策粗糙集

由2.2節可以看出，決策粗糙集是基于單個決策誤判代價矩陣構建的，且誤判代價矩陣通常是由領域專家給定，因而獲得的決策規則及決策代價存在局限性。文獻[5-6]對多重代價決策粗糙集進行了討論，構建了樂觀代價決策粗糙集和悲觀代價決策粗糙集。

設M1,M2,…,Mm為m個不同的決策誤判代價矩陣，則第i(i=1,2…,m)個決策誤判代價矩陣如表2所示。由m個決策誤判代價矩陣，對應得到m個(α,β)閾值，考慮m個閾值中最小值和最大值的情況，根據第i個決策誤判代價矩陣和式（2），可計算得到第i個閾值 (αi,βi)為：

Table 2 i-th cost matrix表2 第i個代價矩陣

根據閾值 (αi,βi)和2.2節中的決策規則（P）、（B）和（N），可分別得到基于容差關系的樂觀代價決策規則和悲觀代價決策規則。

樂觀代價決策規則表示為：

悲觀代價決策規則表示為：

若令Pr(Dmax(TP(x))|TP(x))=l，則基于樂觀代價決策粗糙集的總體決策代價可定義為：

基于悲觀代價決策粗糙集的總體決策代價可定義為：

通過研究樂觀和悲觀代價決策粗糙集來判定決策規則，能預測整個信息系統的最小和最大總體決策代價。但在實際生活中專家給定的誤判代價矩陣主觀性較強，且每個專家在領域的認可度差別較大，而在智能決策信息系統的研究過程中，人們往往希望獲得的決策誤判代價更具有代表性和一般性準則，以提高決策規則的可信度。因此，本文將權重均值代價策略引入決策粗糙集中，提出一種基于權重多重代價的決策粗糙集模型。

定義3（代價認可度）設M1,M2,…,Mm為m個不同專家給出的決策誤判代價矩陣，假設第i個代價矩陣如表2所示。令φij=[φi1,φi2,…,φin]代表領域用戶對第i個專家的n個認可度評價，則每個代價矩陣的認可度可通過專家的認可度來描述。m個決策誤判代價認可度可用矩陣描述如下：

在實際應用中，可通過計算每位專家n個認可度評價的平均值作為該專家的認可度，則第i個專家的代價認可度權重定義為：

ωi值越大，說明該領域專家在領域用戶中的認可度評價越高，其給出的決策代價矩陣可信度越高，因此對應的決策代價矩陣權重越大。記m個代價矩陣的認可度權重為：

根據式（3）和式（4），可計算得到基于權重多代價的閾值 (α′,β′),其值分別為：

則基于權重多重代價的容差決策粗糙集模型正區域、邊界域和負區域的決策規則可表示為：

則基于權重多重代價決策粗糙集的總體決策代價可定義為：

4 基于權重多重代價的多粒度決策粗糙集

4.1 權重多重代價的多粒度決策粗糙集

給定不完備決策信息系統S=(U,C∪D,V,f)，令A1,A2,…,Am為條件屬性C的m個屬性子集，其誘導的容差關系簇{TA1,TA2,…,TAm}稱為m粒度空間結構。假設在每個粒度結構下，其狀態集均用Ω={X,XL}表示，對應的決策動作集A={αP,αN,αB}，其決策誤判代價矩陣由m個不同的專家給出，其權重記為φ=，假設在每個粒度結構下，決策代價矩陣相同，則任意對象x執行決策αP、αN、αB的期望損失可表示為：

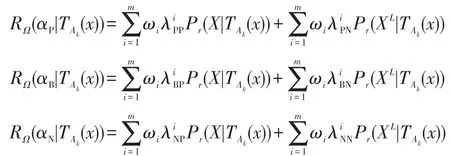
根據三支決策原則和悲觀多粒度粗糙集，執行決策αP、αN、αB的期望損失可表示為：

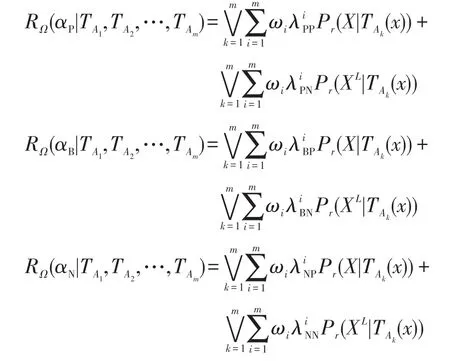
其中∨表示取Pr(X|TAk(x)),k=1,2,…,m中的最大值。

根據三支決策原則和樂觀多粒度粗糙集，執行決策αP、αN、αB的期望損失可表示為:

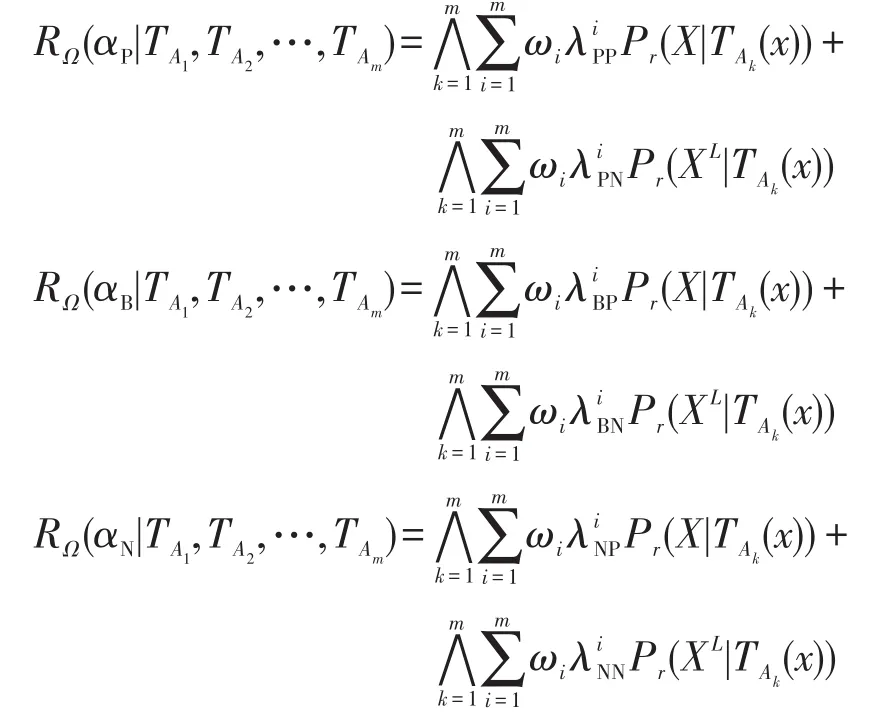
其中∧表示取Pr(X|TAk(x)),k=1,2,…,m中的最小值。

下面將針對基于權重多重代價的悲觀多粒度決策粗糙集模型進行分析。由前面描述可知，Pr(X|TAk(x))+Pr(XL|TAk(x))=1，則執行決策αP、αN、αB的期望損失可表示為：

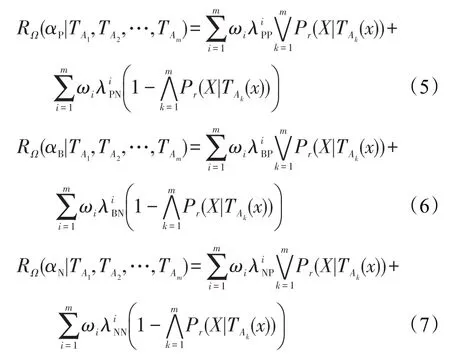
根據貝葉斯風險決策規則可得：

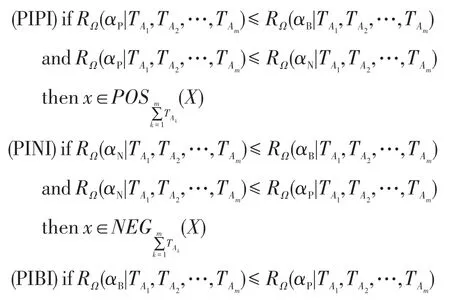
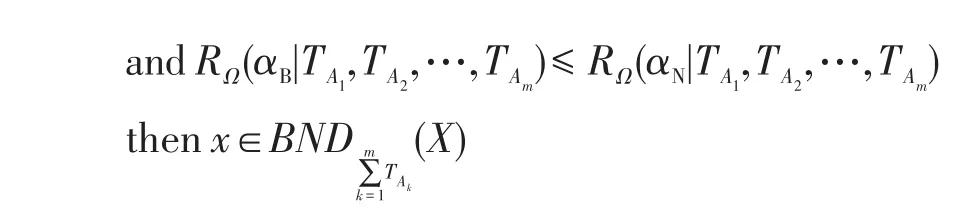
根據規則（PIPI）和式（5）得到：

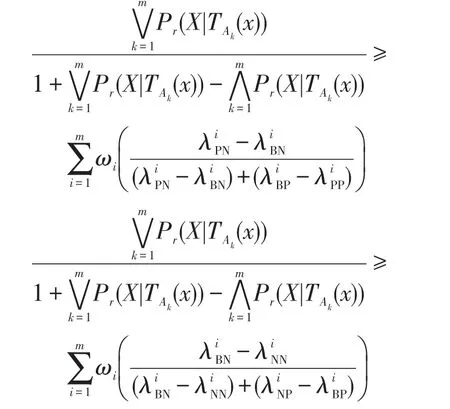
根據規則（PINI）和式（6）得到:

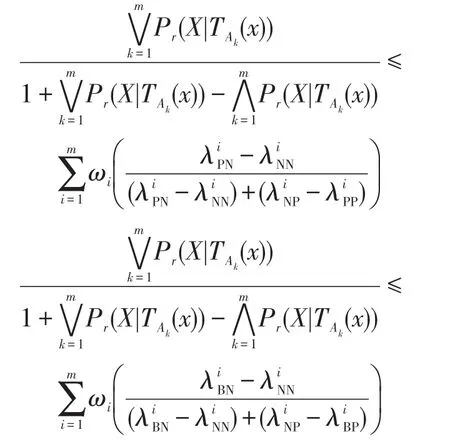
根據規則（PIBI）和式（7）得到：

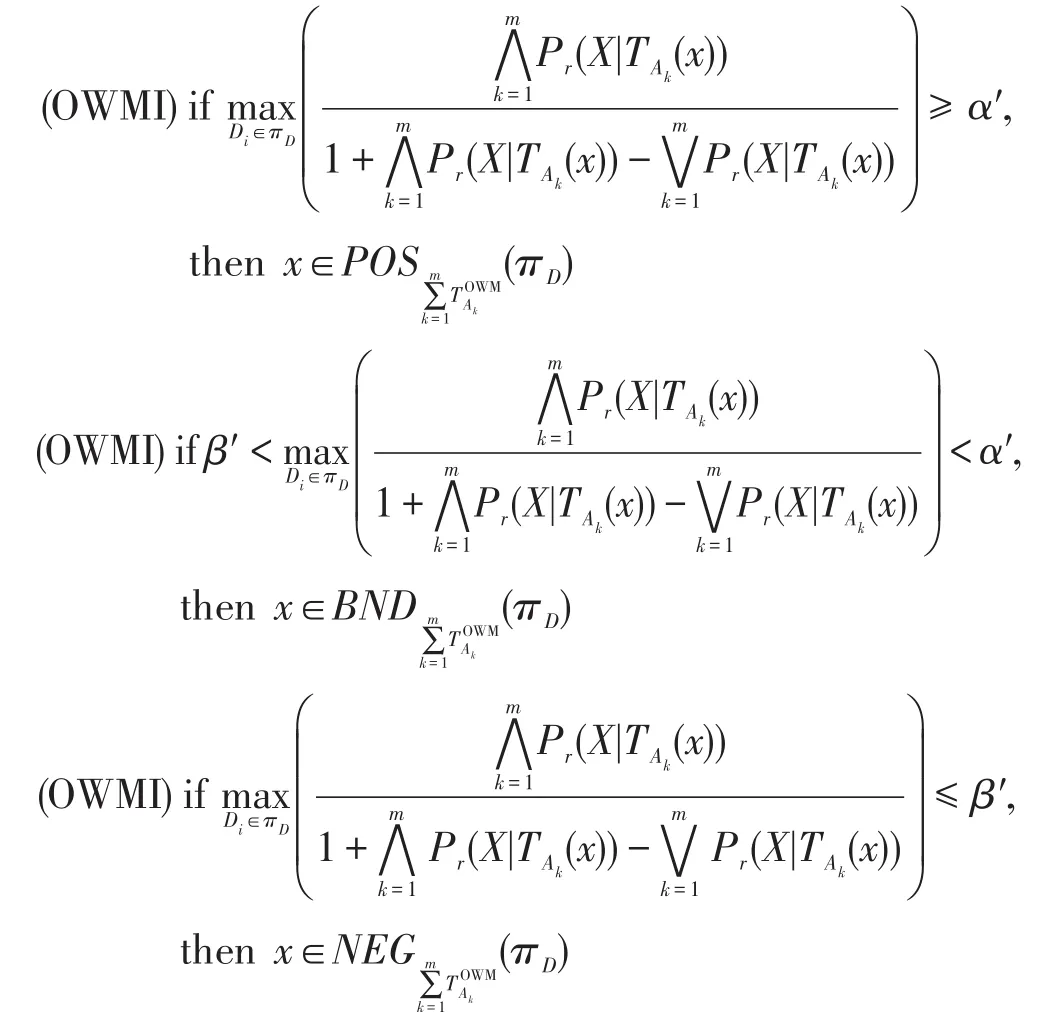
則1≥α′≥β′≥0，得到基于權重多重代價的悲觀多粒度決策粗糙集下的正區域、邊界域和負區域的決策規則可表示為：

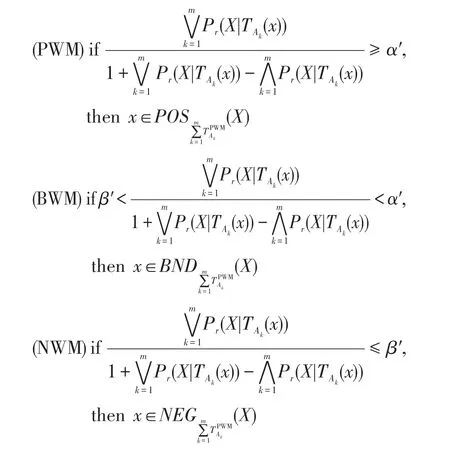
用相同的分析方法，可以得到權重多重代價的樂觀多粒度決策粗糙集下的正區域、邊界域和負區域的決策規則可表示為：

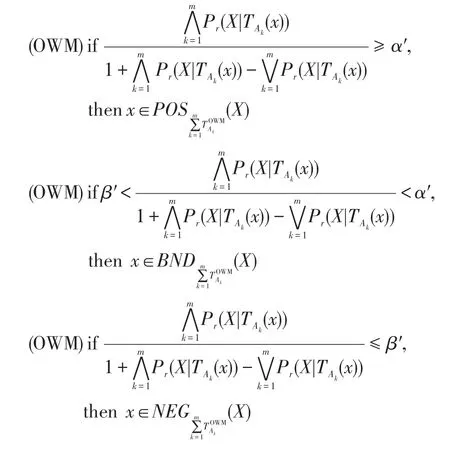
定義4給定一個不完備決策信息系統S=(U,C∪D,V,f)，令A1,A2,…,Am為條件屬性C的m個屬性子集，其誘導的容差關系簇為{TA1,TA2,…,TAm}，對于?X?U，則X關于屬性子集A1,A2,…,Am基于權重多重代價的悲觀多粒度決策粗糙集下的正區域、邊界域和負區域定義為：

基于權重多重代價的悲觀多粒度決策粗糙集X的上、下近似集可定義為：

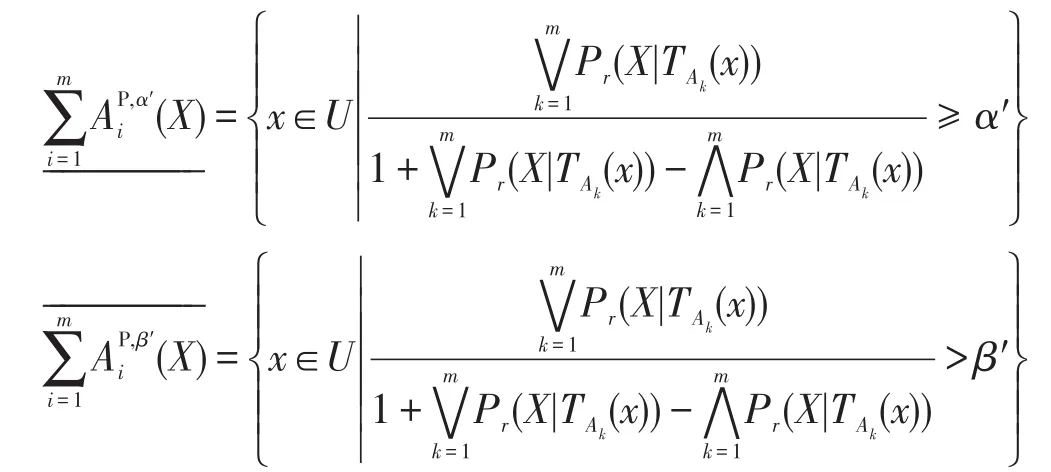
定義5給定一個不完備決策信息系統S=(U,C∪D,V,f)，令A1,A2,…,Am為條件屬性C的m個屬性子集，其誘導的容差關系簇為{TA1,TA2,…,TAm}，對于?X?U，則X關于屬性子集A1,A2,…,Am基于權重多重代價的樂觀多粒度決策粗糙集下的正區域、邊界域和負區域定義為：

基于權重多重代價的悲觀多粒度決策粗糙集X的上、下近似集可定義為：

4.2 基于權重多重代價的多粒度決策粗糙集模型相關性質與決策代價

根據權重多重代價的悲觀多粒度決策粗糙集模型和樂觀多粒度決策粗糙集模型的上、下近似集定義，當α′=1，β′=0時，可以得到：

當m=1時，可以得到：

顯然，悲觀多粒度決策粗糙集當α′=1，β′=0時即為多粒度粗糙集；當m=1時即為決策粗糙集。

定理1設S=(U,C∪D,V,f)是一個不完備決策信息系統，令A1,A2,…,Am為條件屬性C的m個屬性子集族，P:2U→[0,1]是定義在冪集2U上的概念函數，對任意1≥α′≥β′≥0和X?U,有以下性質成立：

以上性質根據定義4和定義5很容易證明。

定義6給定一個不完備決策信息系統S=(U,C∪D,V,f)，令A1,A2,…,Am為條件屬性C的m個屬性子集，其誘導的容差關系簇為{TA1,TA2,…,TAm}，由決策屬性D導出的劃分πD={D1,D2,…,Dm}，對?x∈U，基于權重多重代價悲觀多粒度決策粗糙集下的(α′,β′)-正區域、邊界域和負區域的決策規則可表示為：

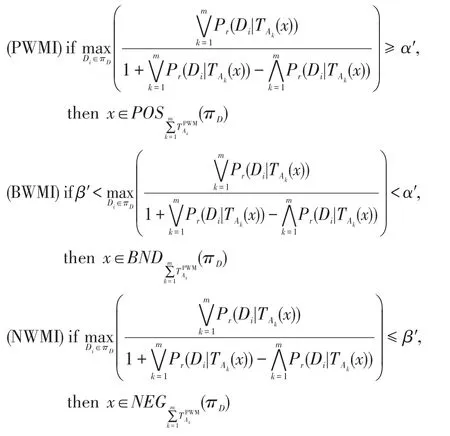
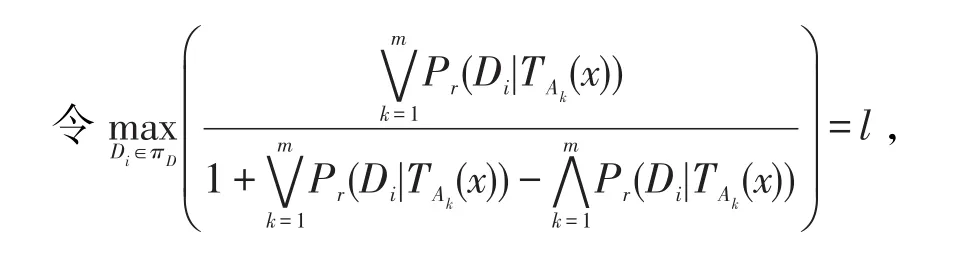
表示在所有滿足條件的決策類中，對象x被劃分到最大可能性的決策類中，則基于權重多重代價悲觀多粒度決策粗糙集的總體決策代價可表示為：

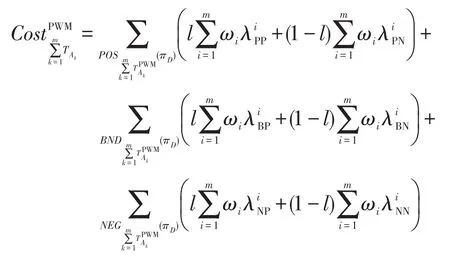
基于權重多重代價樂觀多粒度決策粗糙集下的(α′,β′)-正區域、邊界域和負區域的決策規則可表示為：

則總體決策代價可表示為：

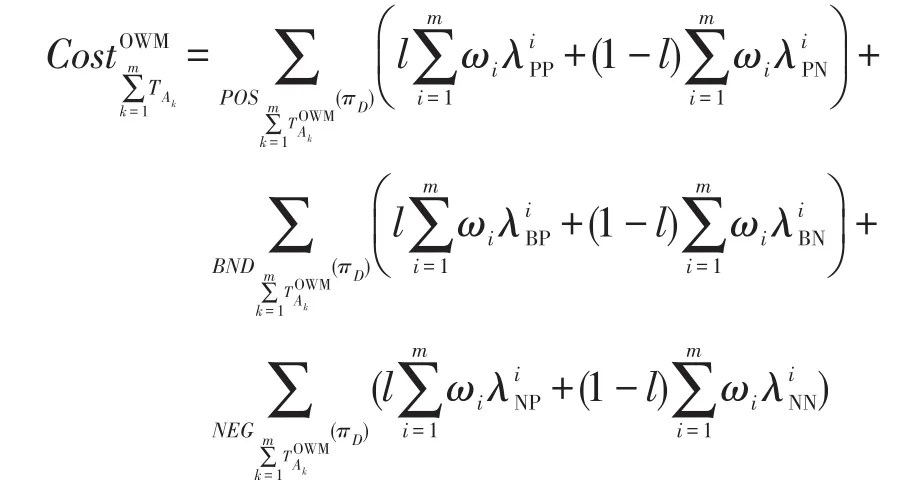
5 粒度約簡方法

屬性約簡是決策粗糙集理論研究的一個重要內容。在多粒度環境下的目標決策中，通過粒度約簡去除那些冗余的知識粒度也是多粒度粗糙集模型中的關鍵問題。本文將多粒度思想和決策粗糙集模型結合，構建了基于權重多重代價的多粒度決策粗糙集模型，其本質上仍然具有決策粗糙集模型的性質。文獻[11-14]從不同角度給出了一系列的決策粗糙集的屬性約簡方法。文獻[12]對決策粗糙集的屬性約簡準則進行了研究，即決策單調性準則、一般性準則和代價準則。文獻[14]討論了幾種與正域相關的決策粗糙集屬性約簡定義，提出一種保正域不變的決策粗糙集屬性約簡。下面以基于權重多重代價的悲觀多粒度決策粗糙集為例，分析其正域隨粒度的變化情況，并提出一種基于最小代價的粒度約簡方法。

定理2設不完備決策信息系統S=(U,C∪D,V,f)，令A={A1,A2,…,Am}為條件屬性C的m個屬性子集族，(α′,β′)為滿足條件的一對閾值，給定A′?A,X∈U/D，則不成立。

證明若證明不成立，只需找到任意對象x∈AP,α′i(X)滿足即可。令粒度空間A′誘導的最大值，最小值，假設Ai∈A′且滿足Pr(X|TAi(x))=,則，即若，則滿足m≥α′。根據公式：

由定理2可知，基于權重多重代價的悲觀多粒度決策粗糙集中，其正域并不隨粒度的變化而單調性變化，因此采用正域不變的方法對粒度約簡在理論性和可解釋性上有一定的困難。根據定義6中基于權重多重代價多粒度決策粗糙集的總體決策代價的計算方法，本文以基于權重多重代價悲觀多粒度決策粗糙集為例，提出一種基于代價最小的粒度約簡定義。

定義7設不完備決策信息系統S=(U,C∪D,V,F)，令A={A1,A2,…,Am}為條件屬性C的m個粒度空間集合，其誘導的容差關系簇為{TA1,TA2,…,TAm},知識粒度集A′?A是關于權重多重代價悲觀多粒度決策粗糙集模型中的一個粒度約簡，當且僅當滿足：

6 結束語

決策粗糙集模型是根據Bayes風險決策理論，通過分析各種決策的風險代價，從而找出最小風險代價的決策；多粒度粗糙集模型是從多粒度、多層次角度對決策問題進行分析。本文將決策粗糙集和多粒度粗糙集進行有效結合，在分析多重代價決策粗糙集模型和多粒度粗糙集模型的基礎上，提出一種基于權重多重代價的多粒度決策粗糙集模型，該模型拓寬了決策粗糙集模型的應用領域；同時，在不完備信息系統中，分析了悲觀代價決策粗糙集、樂觀代價決策粗糙集和權重多重代價多粒度決策粗糙集模型的決策規則和決策風險代價，并給出了一種基于代價最小化的粒度約簡方法，為多粒度粗糙集模型的粒度約簡問題提出了一個新思路。

[1]Pawlak Z.Rough sets[J].International Journal of Computer&Information Sciences,1982,11(5):341-356.

[2]Miao Duoqian,Li Daoguo.Rough set theory,algorithm and application[M].Beijing:Science Press,2007.

[3]Yu Hong,Wang Guoyin,Yao Yiyu.Current research and future perspective on decision-theoretic rough sets[J].Chinese Journal of Computers,2015,38(8):1628-1639.

[4]Li Huaxiong,Zhou Xianzhong.Risk decision making based on decision-theoretic rough set:a three-way view decision model[J].International Journal of Computational Intelligence Systems,2011,4(1):1-11.

[5]Dou Huili,Yang Xibei,Song Xiaoning,et al.Decision-theoretic rough set:a multicost strategy[J].Knowledge-Based Systems,2016,91:71-83.

[6]Ma Xingbin,Ju Hengrong,Yang Xibei,et al.Multi-cost based decision-theoretic rough sets in incomplete information systems[J].Journal of Nanjing University:Natural Sciences,2015,51(2):335-342.

[7]Yang Xiaoping,Yao Jingtao.Modelling multi-agent threeway decisions with decision-theoretic rough sets[J].Fundamenta Informaticae,2012,115(2):157-171.

[8]Meng Chao,Yu Jiankun.Merging three-way decisions with decision-theoretic rough sets[J].Computer Systems&Applications,2016,25(4):175-179.

[9]Yao Yiyu.Decision-theoretic rough set models[C]//LNCS 4481:Proceedings of the 2nd International Conference on Rough Sets and Knowledge Technology,Toronto,May 14-16,2007.Berlin,Heidelberg:Springer,2007:1-12.

[10]Yao Yiyu,Zhao Yan.Attribute reduction in decision-theoretic rough set models[J].Information Sciences,2008,178(17):3356-3373.

[11]Jia Xiuyi,Liao Wenhe,Tang Zhenmin,et al.Minimum cost attribute reduction in decision-theoretic rough set models[J].Information Sciences,2013,219:151-167.

[12]Ju Hengrong,Yang Xibei,Yu Hualong,et al.Research on attribute reduction criteria in decision-theoretic rough set[J].Journal of Nanjing Normal University:Natural Science Edition,2015,38(1):41-47.

[13]Ma Xi'ao,Wang Guoyin,Yu Hong.Heuristic method to attribute reduction for decision region distribution preservation[J].Journal of Software,2014,25(8):1761-1780.

[14]Huang Guoshun.Positive region preservation reducts in deci-sion-theoretic rough set models[J].Computer Engineering andApplications,2016,52(2):165-169.

[15]Qian Yuhua,Liang Jiye,Yao Yiyu,et al.MGRS:a multigranulation rough set[J].Information Sciences,2010,180(6):949-970.

[16]Zhang Ming,Cheng Ke,Yang Xibei,et al.Multigranulation rough set based on weighted granulations[J].Control and Decision,2015,30(2):222-228.

[17]Xu Yi,Li Ce.A variable precision multi-granulation rough set model based on multiple thresholds[J].Computer Engineering and Science,2016,38(8):1727-1734.

[18]Meng Huili,Ma Yuanyuan,Xu Jiuchen.Granularity reduction of variable precision pessimistic multi-granulation rough set based on granularity entropy of lower approximate distribution[J].Computer Science,2016,43(2):83-85.

[19]Yao Yiyu,She Yanhong.Rough set models in multigranulation spaces[J].Information Sciences,2016,327:40-56.

[20]Ju Hengrong,Li Huaxiong,Yang Xibei,et al.Cost-sensitive rough set:a multi-granulation approach[J].Knowledge-Based Systems,2017,123:137-153.

[21]Qian Yuhua,Zhang Hu,Sang Yanli,et al.Multigranulation decision-theoretic rough sets[J].International Journal ofApproximate Reasoning,2014,55(1):225-237.

[22]Yang Hailong,Guo Zhilian.Multigranulation decision-theoretic rough sets in incomplete information systems[J].International Journal of Machine Learning and Cybernetics,2015,6(6):1005-1018.

[23]Xu Weihua,Guo Yanting.Generalized multigranulation doublequantitative decision-theoretic rough set[J].Knowledge-Based Systems,2016,105:190-205.

[24]Liu Caihui,Pedrycz W,Wang Meizhi.Covering-based multigranulation decision-theoretic rough sets[J].Journal of Intelligent&Fuzzy Systems,2017,32(1):749-765.

[25]Qian Yuhua,Liang Xinyan,Lin Guoping,et al.Local multigranulation decision-theoretic rough sets[J].International Journal ofApproximate Reasoning,2017,82:119-137.

附中文參考文獻:

[2]苗奪謙,李道國.粗糙集理論、算法與應用[M].北京:科學出版社,2007.

[3]于洪,王國胤,姚一豫,等.決策粗糙集理論研究現狀與展望[J].計算機學報,2015,38(8):1628-1639.

[6]馬興斌,鞠恒榮,楊習貝,等.不完備信息系統中的多重代價決策粗糙集[J].南京大學學報:自然科學版,2015,51(2):335-342.

[8]孟超,余建坤.三支決策與決策粗糙集融合模型[J].計算機系統應用,2016,25(4):174-179.

[12]鞠恒榮,楊習貝,于化龍,等.決策粗糙集的屬性約簡準則研究[J].南京師大學報:自然科學版,2015,38(1):41-47.

[13]馬希驁,王國胤,于洪.決策域分布保持的啟發式屬性約簡方法[J].軟件學報,2014,25(8):1761-1780.

[14]黃國順.保正域的決策粗糙集屬性約簡[J].計算機工程與應用,2016,52(2):165-169.

[16]張明,程科,楊習貝,等.基于加權粒度的多粒度粗糙集[J].控制與決策,2015,30(2):222-228.

[17]徐怡,李策.基于多重閾值的變精度多粒度粗糙集模型[J].計算機工程與科學,2016,38(8):1727-1734.

[18]孟慧麗,馬媛媛,徐久成.基于下近似分布粒度熵的悲觀多粒度粗糙集約簡[J].計算機科學,2016,43(2):83-85.