基于自組織映射的改進BP神經(jīng)網(wǎng)絡(luò)短期光伏出力預(yù)測研究

， ， ，，·(.國網(wǎng)新疆電力有限公司電力科學(xué)研究院，新疆 烏魯木齊 800；.國網(wǎng)新疆電力有限公司經(jīng)濟技術(shù)研究院，新疆 烏魯木齊 8006；.國網(wǎng)淮南供電公司，安徽 淮南 007；.新奧泛能網(wǎng)絡(luò)科技股份有限公司，河北 廊坊 065600)

0 引 言

隨著環(huán)境壓力不斷增加，中國大力發(fā)展光伏發(fā)電這種可再生能源[1-2]。雖然光伏發(fā)電具有無污染等優(yōu)點，但其出力因氣候變化而隨機波動給光伏電站并網(wǎng)帶來巨大困擾，讓電力系統(tǒng)的穩(wěn)定性受到影響[3]。為了解決這一問題，國內(nèi)外學(xué)者提出對光伏出力進行預(yù)測，讓電力調(diào)度部門能夠提前做出判斷，降低波動影響以提高穩(wěn)定性。

目前主流的光伏預(yù)測模型有3種，分別為人工智能模型[4-6]、統(tǒng)計模型[7-8]和混合模型[9-10]。人工智能模型使用大數(shù)據(jù)處理中的神經(jīng)網(wǎng)絡(luò)和支持向量機等黑箱模型對光伏出力進行直接或間接預(yù)測。文獻[4]使用光伏出力的信息熵作為特征，采用極限學(xué)習(xí)機、廣義回歸神經(jīng)網(wǎng)絡(luò)、徑向基神經(jīng)網(wǎng)絡(luò)分別建立預(yù)測對比，得出極限學(xué)習(xí)機的預(yù)測效果最好。文獻[5]首先對原始數(shù)據(jù)進行小波分解，然后對每層數(shù)據(jù)使用神經(jīng)網(wǎng)絡(luò)進行預(yù)測，最后對預(yù)測數(shù)據(jù)進行重構(gòu)得到結(jié)果。文獻[6]使用天氣模式下的光伏波動作為特征，使用EMD對原始數(shù)據(jù)進行特征映射，使用IMF分量進行LSSVM預(yù)測，對預(yù)測結(jié)果進行等權(quán)值求和得到光伏出力預(yù)測。統(tǒng)計模型采用數(shù)理統(tǒng)計的方法，對光伏出力進行聯(lián)合概率分布擬合，得到光伏出力的概率模型。文獻[7]對不同天氣下的光伏出力用K-means進行聚類，統(tǒng)計有功出力的實際邊緣分布和預(yù)測邊緣分布，以最優(yōu)擬合作為目標(biāo)對不同種類的Copula函數(shù)參數(shù)進行識別，得到先驗條件下誤差的條件概率分布，并對預(yù)測結(jié)果進行修正。文獻[8]使用混沌理論建立光伏出力的向空間，建立其混沌預(yù)測模型得到良好的預(yù)測結(jié)果。混合模型是將人工智能模型與概率模型進行融合的預(yù)測模型。文獻[9]對徑向基神經(jīng)網(wǎng)絡(luò)的邊界進行評估，以減少預(yù)測模型中累計誤差，取得良好結(jié)果。文獻[10]使用灰色模型建立統(tǒng)計后的相似日時刻出力，使用灰色模型回歸結(jié)果和采樣日的溫度建立神經(jīng)網(wǎng)絡(luò)預(yù)測模型得到預(yù)測結(jié)果。

國內(nèi)主流預(yù)測模型的采樣間隔通常選擇1 h，但是采樣間隔過大，這會平滑光伏出力的實際波動。在前人基礎(chǔ)上，所提出的短期光伏預(yù)測方法其采樣間隔為5 min，詳細顯示了原始數(shù)據(jù)中的波動，提高了預(yù)測精度。采用SOM對光伏歷史數(shù)據(jù)組進行聚類降維，采用PSO對BP神經(jīng)網(wǎng)路進行優(yōu)化，最后得到16 h的光伏出力預(yù)測模型，通過仿真驗證所提模型具有良好的預(yù)測效果。

1 原始數(shù)據(jù)的降維處理

1.1 原始數(shù)據(jù)說明

光伏發(fā)電主要受太陽輻射影響，而太陽輻射又與溫度、濕度、風(fēng)速等氣候因素有關(guān)。在眾多環(huán)境參數(shù)中如何選擇與光伏出力最相關(guān)的環(huán)境變量，從而降低預(yù)測模型輸入維數(shù)，減少模型訓(xùn)練時間是建立光伏預(yù)測模型首先需要考慮的問題。

選用澳大利亞的Yulara光伏發(fā)電站數(shù)據(jù)，其額定功率為1 058.4 kW，地面固定式安裝。數(shù)據(jù)中的環(huán)境變量有：光伏有功出力(active power, AP)， kW；地面水平輻射(global horizontal radiation, GHR)，W/m2；彌散性輻射(diffuse horizontal radiation, DHR)，W/m2；環(huán)境溫度(weather temperature, WT)，℃；環(huán)境相對濕度(weather relative humidity, WRH)，%；風(fēng)速(wind speed, WS)，m/s；風(fēng)向(wind direction, WD)，°。選取2017年8月光伏電站數(shù)據(jù)組作為預(yù)測模型的訓(xùn)練數(shù)據(jù)和測試數(shù)據(jù)。

原始數(shù)據(jù)總共有8 912×7個點，記錄時間從8月1日至8月31日，采樣間隔時間為5 min。由于數(shù)據(jù)過多，故只將AP、GHR作為代表給出，見圖1所示。

圖1 8月的AP和GHR數(shù)據(jù)

從圖1中可以得到AP最大值為439.545 3 kW，最小值為0；GHR最大值為955.111 8 W/m2，最小值為0。可以看出AP和GHR具有很強的趨勢相關(guān)性，通過皮爾遜相關(guān)系數(shù)計算可得到AP和GHR的相關(guān)度為0.503 2。為了提高預(yù)測精度，將7組環(huán)境變量進行歸一化，見式(1)。考慮到夜間光伏電站無有功功率輸出，故在原始數(shù)據(jù)中去除輸出為0的部分，僅將每日有功輸出部分進行連接，得到31日的光伏電站數(shù)據(jù)組見圖2。

(1)

圖2 Yulara光伏電站歸一化后的數(shù)據(jù)組

從圖2中可得，在8月數(shù)據(jù)中AP變化具有一定周期性，每日出力曲線整體呈現(xiàn)M型。在第2日AP劇烈波動的同時，GHR、DHR和WHR也出現(xiàn)大幅變化，而發(fā)生變化時間滯后于AP，尤其是WHR出現(xiàn)類似階躍信號一般的陡增，暗示此日出現(xiàn)了突然降雨影響了AP輸出，WT、WS和WD數(shù)據(jù)未能直觀看出與AP波動有何關(guān)系；第10日，當(dāng)AP發(fā)生劇烈變化時，GHR、DHR沒有同步出現(xiàn)波動，但WT數(shù)據(jù)出現(xiàn)增長。從以上數(shù)據(jù)中可以得到光伏出力在環(huán)境沒有出現(xiàn)大幅變化時，從每日尺度上看到光伏出力具有周期性，但具體到某1日中的某一時刻，其輸出具有很強的隨機波動。

1.2 自組織映射SOM

自組織映射(self-organization mapping, SOM)于1982年由Kohonen提出，用于解決非線性空間內(nèi)的分類問題。它能根據(jù)高維數(shù)據(jù)通過自我競爭學(xué)習(xí)得到其最大相關(guān)組，即最優(yōu)分類。一個標(biāo)準(zhǔn)的SOM結(jié)構(gòu)如圖3所示。x1，x2，…，xm為輸入信號，經(jīng)過輸入層節(jié)點進入競爭層，競爭層由一個二維神經(jīng)節(jié)點陣列組成，在節(jié)點權(quán)重信號更新過程中，競爭層中獲勝的神經(jīng)節(jié)點會自動將輸入信號自動向其靠攏，最終得到輸入信號的分類。

圖3 標(biāo)準(zhǔn)SOM結(jié)構(gòu)

建立SOM分類模型，首先是根據(jù)輸出信號種類確定競爭層節(jié)點數(shù)，并對節(jié)點進行隨機權(quán)重賦值；接著計算節(jié)點權(quán)重向量與輸出數(shù)據(jù)之間的距離，目前常用的向量距離計算公式見式(2)、式(3)和式(4)；然后選擇向量距離最小的節(jié)點為競爭層獲勝節(jié)點；使用式(5)更新節(jié)點的權(quán)重，讓獲勝節(jié)點向最優(yōu)分類靠近；通過自適應(yīng)梯度下降法更新學(xué)習(xí)速率和領(lǐng)域大小，重新計算向量距離；最后經(jīng)過不斷迭代，得到最優(yōu)分類模式。

Box距離：

d=max(|xi-w11|，|xi-w12|，…，|xi-wij|)

(2)

歐式距離：

(3)

曼哈頓距離(出租車距離)：

(4)

式(2)、式(3)和式(4)中：X為輸入層向量，即輸入信號x1，x2，…，xm；W為競爭層神經(jīng)節(jié)點權(quán)重向量。

更新權(quán)重計算公式：

W(n+1)=W(n)+Θ(n)α(n)[X(n)-W(n)]

(5)

式中：W為權(quán)重向量；n為迭代次數(shù)；Θ為領(lǐng)域函數(shù)；α為學(xué)習(xí)速率；X為輸入向量。

對圖2中的數(shù)據(jù)進行劃分，將第1日至第29日數(shù)據(jù)作為預(yù)測模型的訓(xùn)練數(shù)據(jù)，將第30日和第31日數(shù)據(jù)作為測試數(shù)據(jù)。使用所提出的SOM分類方法，網(wǎng)絡(luò)結(jié)構(gòu)為2×2；向量距離選用歐式距離，分類結(jié)果見圖4。

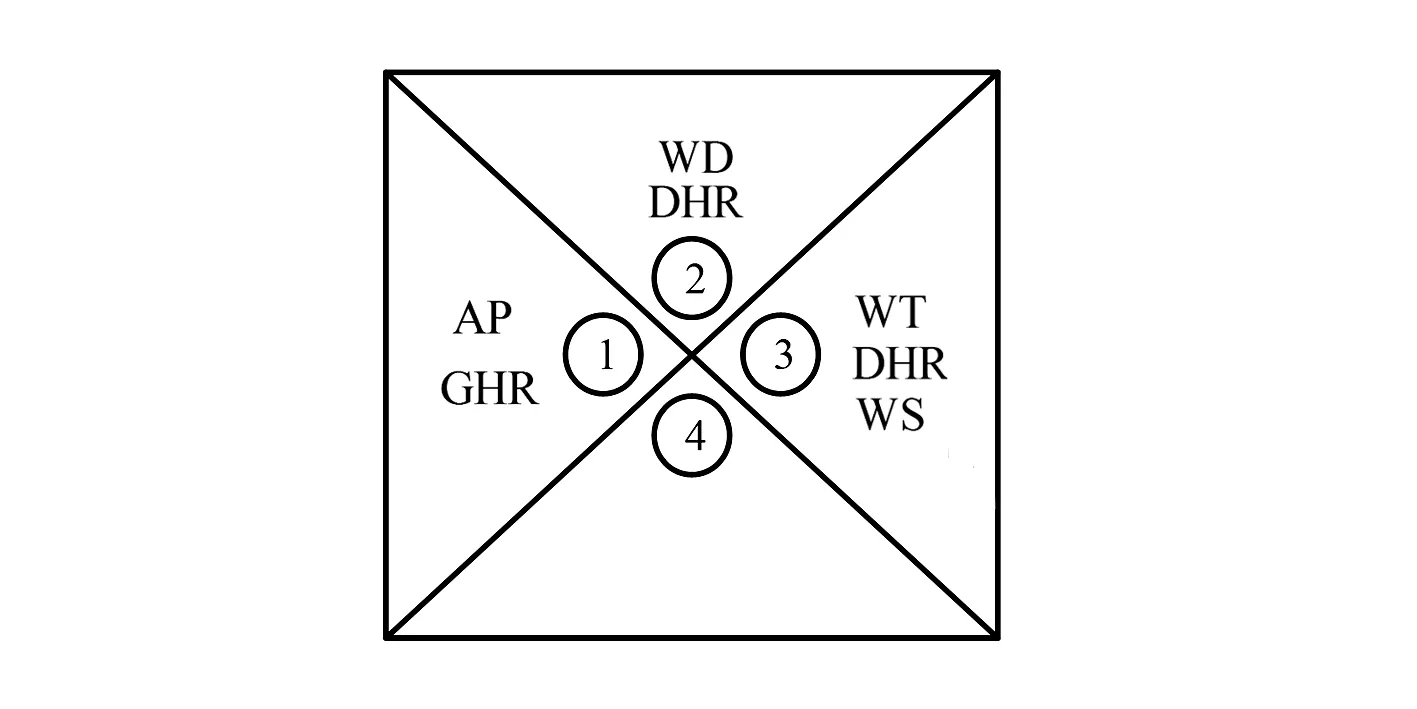
圖4 SOM對7類數(shù)據(jù)的分類結(jié)果

從圖4的分類結(jié)果來看，WT、DHR、WS被劃為3組，與之差異較大的AP和GHR劃為1組，而WD和DHR雖與1組和3組都相似，但又不能單獨劃為其中一類，故在其后的BP神經(jīng)網(wǎng)絡(luò)訓(xùn)練模型中使用AP、GHR、DHR和WD作為輸入向量。

2 基于SOM-PSO-BP的短期預(yù)測模型

2.1 BP神經(jīng)網(wǎng)絡(luò)

BP神經(jīng)網(wǎng)絡(luò)——反向傳播神經(jīng)網(wǎng)絡(luò)(back-propagation neural networks)由3層節(jié)點組成：輸入層、隱藏層和輸出層，一個結(jié)構(gòu)為3-4-2，即3個輸入節(jié)點、4個隱藏節(jié)點、2個輸出節(jié)點的典型神經(jīng)網(wǎng)絡(luò)見圖5所示。輸入信號經(jīng)過輸入層向前傳播，經(jīng)過隱藏層和輸出層作用得到輸出信號。輸出信號與實際測量信號之間的誤差，又通過反向通道向后修正神經(jīng)網(wǎng)絡(luò)節(jié)點的權(quán)值來減少輸出誤差，使輸出結(jié)果不斷逼近真實信號，所以稱作反向傳播神經(jīng)網(wǎng)絡(luò)。

以圖5所示的BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)為例，輸入X=[x1,x2,x3]T，輸出Y=[y1,y2]T，W為神經(jīng)節(jié)點權(quán)重矩陣，見式(6)所示，從輸入層到隱藏層的映射見式(7)，其中B為偏執(zhí)矩陣，U=[Uk1,Uk2,Uk3,Uk4]T為隱藏層的線性組合結(jié)果，從隱藏層到輸出層的映射見式(8)所示，其中f為激活函數(shù)，在神經(jīng)網(wǎng)絡(luò)中常用的有：sigmod、tanh-sig和高斯徑向基。

(6)

U=f(Wk·X+Bk)

(7)

Y=f(Wj·U+Bj)

(8)

圖5 結(jié)構(gòu)為3-4-2的典型神經(jīng)網(wǎng)絡(luò)

在BP神經(jīng)網(wǎng)絡(luò)計算過程中，從輸出向輸入側(cè)不斷傳遞誤差，同時使用梯度下降法對隱藏層和輸出層中的權(quán)值矩陣進行修改以降低誤差，最終將輸出誤差降低到給定值。

在BP算法中，神經(jīng)網(wǎng)絡(luò)對初始神經(jīng)節(jié)點權(quán)重矩陣W和偏執(zhí)矩陣B會進行隨機賦值，這有可能讓自適應(yīng)梯度算法陷入局部最優(yōu)解，導(dǎo)致輸出結(jié)果差異很大。為了解決這一問題，采用粒子群算法(particle swarm optimization，PSO)對權(quán)重矩陣W和偏執(zhí)矩陣B進行尋優(yōu)，加快BP網(wǎng)絡(luò)收斂速度和精度。

2.2 使用PSO對BP神經(jīng)網(wǎng)絡(luò)參數(shù)尋優(yōu)

根據(jù)SOM的分類結(jié)果，選用4-13-1的網(wǎng)絡(luò)結(jié)構(gòu)，即4個輸入層節(jié)點、 13個隱藏層節(jié)點和1個輸出層節(jié)點。粒子群算法優(yōu)化流程見圖6，以權(quán)重矩陣W和偏執(zhí)矩陣B為優(yōu)化目標(biāo)，以均方誤差MSE為評價函數(shù)，如式(9)所示，使用BP神經(jīng)網(wǎng)絡(luò)進行迭代計算，訓(xùn)練集使用前29日的測量數(shù)據(jù)用于建立GA-BP預(yù)測模型，最終得到最優(yōu)結(jié)果，迭代結(jié)果見圖7。

(9)

從圖7可以看到，所采用的粒子群算法在迭代90次之后就趨于穩(wěn)定，均方誤差MSE為7.240 1×10-3。從迭代結(jié)果可以看出所提出的預(yù)測模型具有很高的精度。

圖6 粒子群算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)流程

圖7 PSO-BP的迭代結(jié)果

3 算例仿真

以Matlab作為仿真平臺，使用SOM-PSO-BP模型和AMIRA模型進行仿真對比，以圖2所示數(shù)據(jù)中的第1日至第29日作為訓(xùn)練數(shù)據(jù)，用于建立兩種預(yù)測模型，以第30日和第31日數(shù)據(jù)對模型進行測試，以均方誤差MSE作為評價指標(biāo)檢驗預(yù)測模型的精度。

3.1 ARIMA預(yù)測模型及預(yù)測結(jié)果

累積式自回歸滑動平均(auto regressive integrated moving average, ARIMA)模型被廣泛應(yīng)用于金融、電價預(yù)測[11-12]等領(lǐng)域。預(yù)測模型通常將非平穩(wěn)的歷史數(shù)據(jù)進行有限次差分得到平穩(wěn)時間序列數(shù)據(jù)，然后采用貝葉斯法則對模型的p和q階數(shù)進行尋優(yōu)，最后使用最大似然估計找到模型中的最優(yōu)系數(shù)，得到ARIMA預(yù)測模型。ARIMA的數(shù)學(xué)模型見式(10)所示。

(10)

式中：Δdyt為被d次差分后的yt序列；Φi和θj為ARIMA模型的待評估系數(shù)；εt為t時刻的0均值高斯分布誤差。采用ARIMA對1日至29日的光伏有功出力進行建模，得到30日和31日的預(yù)測結(jié)果和預(yù)測誤差如圖8和圖9所示。

圖8 ARIMA模型的有功出力AP預(yù)測結(jié)果

圖9 ARIMA模型的有功出力AP預(yù)測誤差

從圖8和圖9可以得到，基于ARIMA的光伏預(yù)測模型MSE為0.012 2，誤差最大值為0.338。從誤差分布來看，主要集中在0.15以下，誤差在全部預(yù)測期間的波動都劇烈，沒有明顯的分布特征，由此可以得出ARIMA模型具有有限的預(yù)測精度。

3.2 SOM-PSO-BP預(yù)測結(jié)果

將30日、31日的測試數(shù)據(jù)帶入基于SOM-PSO-BP的光伏出力預(yù)測模型進行計算，得到預(yù)測結(jié)果和預(yù)測誤差如圖10所示。

從圖10和圖11中可以看到，所提出的基于SOM-PSO-BP預(yù)測模型的MSE誤差為2.172 93×10-3，誤差最大值為0.261 6。誤差分布主要集中在0.1以下，在AP的上升段和下降段，預(yù)測數(shù)據(jù)和測試數(shù)據(jù)相差不大，預(yù)測誤差主要集中在光伏出力的低谷時段，在這一時段，光伏出力波動變得劇烈，然而其波動幅值并不大，所以即便在圖7中可以明顯看出預(yù)測誤差偏離測試數(shù)據(jù)較大，但總體誤差并未出現(xiàn)增加。對比圖8、圖9和圖10、圖11，可以得出所提出的SOM-PSO-BP光伏預(yù)測模型在精度上領(lǐng)先ARIMA模型，在MSE指標(biāo)上低一個數(shù)量級，在誤差分布上更加穩(wěn)定，且幅值低。

圖10 SOM-PSO-BP模型的有功出力AP預(yù)測結(jié)果

圖11 SOM-PSO-BP模型的有功出力AP預(yù)測誤差

4 結(jié) 語

光伏出力預(yù)測對電網(wǎng)調(diào)度具有重要意義，通過預(yù)測數(shù)據(jù)能夠及時調(diào)整調(diào)度計劃，穩(wěn)定電網(wǎng)電壓、頻率在正常范圍內(nèi)，提高電能質(zhì)量，降低電網(wǎng)運行風(fēng)險。所提出的基于SOM降維、PSO-BP神經(jīng)網(wǎng)絡(luò)的光伏出力預(yù)測模型，通過光伏發(fā)電站1個月的數(shù)據(jù)對預(yù)測模型進行訓(xùn)練，對比ARIMA預(yù)測模型得到了良好的預(yù)測效果，為解決光伏并網(wǎng)發(fā)電隨機波動無法預(yù)測問題提供了一些建議。

[1] 趙爭鳴, 雷一, 賀凡波, 等.大容量并網(wǎng)光伏電站技術(shù)綜述[J].電力系統(tǒng)自動化, 2011, 35(12):101-107.

[2] 龔鶯飛, 魯宗相, 喬穎, 等.光伏功率預(yù)測技術(shù)[J].電力系統(tǒng)自動化, 2016,40(4):140-151.

[3] 丁明, 王偉勝, 王秀麗,等. 大規(guī)模光伏發(fā)電對電力系統(tǒng)影響綜述[J].中國電機工程學(xué)報, 2014, 34(1):1-14.

[4] Pingzhou Tang, Di Chen, Yushuo Hou. Entropy Method Combined with Extreme Learning Machine Method for the Short-term Photovoltaic Power Generation Forecasting[J].Chaos, Solitons and Fractals, 2015(89):243-248.

[5] Honglu Zhu, Xu Li, Qiao Sun, et al. A Power Prediction Method for Photovoltaic Power Plant Based on Wavelet Decomposition and Artificial Neural Networks[J].Energies, 2016, 9(1):1-15.

[6] 陽霜, 羅滇生, 何洪英, 等. 基于EMD-LSSVM的光伏發(fā)電系統(tǒng)功率預(yù)測方法研究[J].太陽能學(xué)報, 2016, 37(6):1387-1395.

[7] 趙唯嘉, 張寧, 康重慶,等.光伏發(fā)電出力的條件預(yù)測誤差概率分布估計方法[J].電力系統(tǒng)自動化, 2015,39(16):8-15.

[8] Wang Yufe, Sun Lu, Xue Hua. Photovoltaic Output Power Chaotic Characteristic and Trend Prediction Based on the Actual Measurement Data[C].Proceedings of the 2016 IEEE 11th Conference on Industrial Electronics and Applications, 2016, 1(1):326-331.

[9] Chen Jun-Ma, Wang Bing, Lu, Zhou-Xin, et al. Photovoltaic Power Generation Prediction Based on MEA-BP Neural Network[C].2017 32nd Youth Academic Annual Conference of Chinese Association of Automation, 2017,1(1):387-392.

[10] 王守相, 張娜.基于灰色神經(jīng)網(wǎng)絡(luò)組合模型的光伏短期出力預(yù)測[J].電力系統(tǒng)自動化, 2012,36(19):37-41.

[11] 熊志斌.ARIMA融合神經(jīng)網(wǎng)絡(luò)的人民幣匯率預(yù)測模型研究[J].數(shù)量經(jīng)濟技術(shù)經(jīng)濟研究, 2011(6):64-76.

[12] 周明, 聶艷麗,李庚銀,等.基于小波分析的短期電價ARIMA預(yù)測方法[J].電網(wǎng)技術(shù), 2005,29(9):50-55.