基于梁單元和板殼單元混合建模的折疊椅輕量化設計

周美施，尹懷仙，張鐵柱，張洪信，王楠

(青島大學 機電工程學院，山東 青島 266071)

0 引言

現今折疊椅生產企業越來越多，競爭愈發激烈，減輕折疊椅生產成本成為增強企業核心競爭力的關鍵。折疊椅骨架是主要承載構件，對其骨架結構進行輕量化設計，可以節省材料，降低折疊椅生產成本。目前對于折疊椅的有限元分析以及優化設計研究還相對較少。目前產品結構設計方法，主要有拓撲優化和尺寸優化，其中拓撲優化主要應用于產品開發設計階段，對于已經成熟的產品結構沒有太大的實際意義[1-3]，因此本文對某折疊椅產品結構采用尺寸優化設計，減輕折疊椅質量。

傳統的尺寸優化用殼單元模擬折疊椅結構，再針對其殼單元厚度進行尺寸優化，有一定效果，但建模復雜。由于厚度的變化，特別是管件厚度的變化受管件基本管徑的約束，其變化的維度和方向受限，優化效果也受限制。而采用梁單元模擬管件，可以對梁單元管徑和厚度進行優化設計，能在比較大的變量空間尋得最優解，優化效果更好[4-6]。

1 折疊椅有限元模型的建立

折疊椅骨架由材料為Q345的空心圓管、方管組成，Q345彈性模量為2.06×1011MPa，泊松比為0.28，密度為7 850 kg/m3，屈服強度為345 MPa。椅面材料為尼龍布，彈性模量為2.83×109MPa，泊松比為0.4，密度為1 100 kg/m3。通過對折疊椅結構力學特征和結構特征進行分析研究，在ANSYS中建立折疊椅有限元模型，其中折疊椅骨架結構由梁單元模擬，椅面采用殼單元模擬，對折疊椅進行網格劃分，折疊椅有限元模型共有3 614個單元，3 484個節點。折疊椅的有限元模型如圖1所示。

根據調查顯示折疊椅在極限姿態下所受應力最大，因此對折疊在極限姿態下的模型進行有限元分析，其中假設114kg的重物從離椅面40cm高位置自由落體，從接觸椅面到靜止所用時間為0.2s，根據沖量定理計算椅面所受沖擊載荷為1 718N。載荷均布加載到椅面所在節點(圖2)。在有限元計算中，需要消除節點的剛性位移保證剛度矩陣的非奇異，求解出剛度位移矩陣，得到正確的數值解[7-8]。因此需要對折疊椅的模型施加正確的自由度約束，對折疊椅腿與地面接觸的2根矩形梁所在節點施加固定約束。

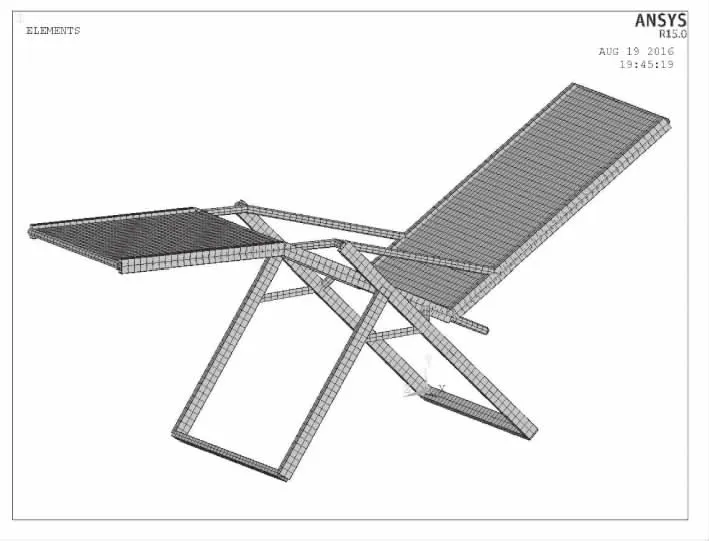
圖1 折疊椅有限元模型

圖2 約束和加載

2 有限元分析結果

通過有限元計算得到折疊椅有限元模型在極限姿態下的應力結果和變形結果。其等效應力云圖如圖3所示，變形云圖如圖4所示。最大等效應力為114MPa，最大應力節點出現在左后支腿與矩橫梁連接位置，與企業實驗得到破壞點一致，驗證了次折疊椅有限元模型的正確性。從折疊椅等效應力云圖可以看出椅面拐角骨架連接處有較小應力較高區域，如圖5所示，其值約為150MPa左右，折疊椅骨架其他部分應力值都較低，根據材料力學中強度公式[9]。對于彈塑性材料，許用應力可用下列公式求解。

σ=σs/n

式中，σ代表折疊椅的許用應力，σs代表Q345的屈服強度，n代表材料的安全系數，其中取n=1.3，Q345的屈服強度為345MPa，因此可以得出折疊椅的許用應力為265MPa。

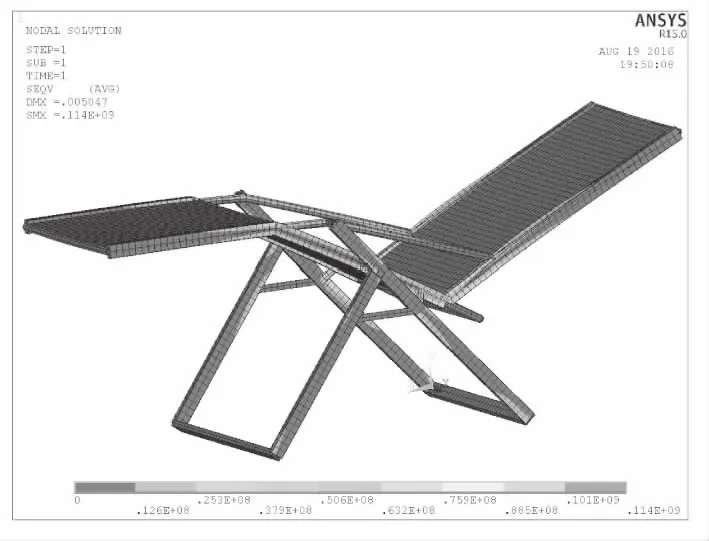
圖3 折疊椅應力云圖

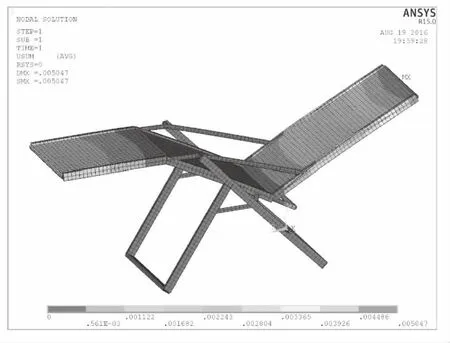
圖4 折疊椅變形云圖

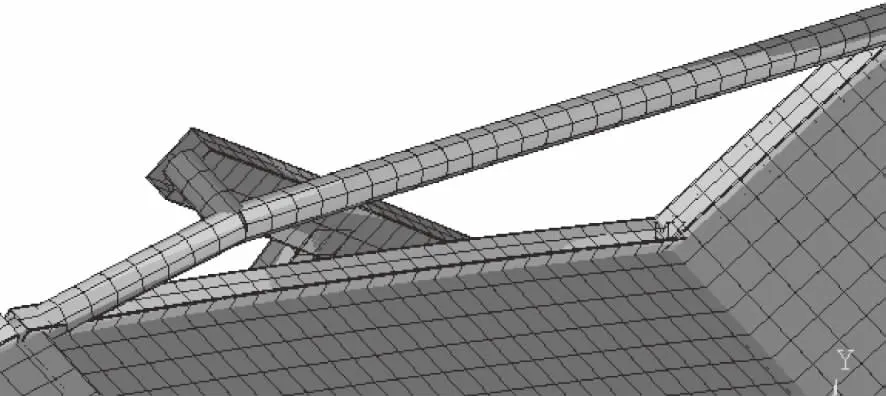
圖5 骨架應力較高區域局部放大圖

通過有限元計算與折疊椅的許用應力值對比可知，折疊椅骨架結構存在較大的強度冗余，可對折疊椅進行輕量化設計，增加材料使用率，降低生產成本。

3 輕量化設計

以折疊椅骨架質量最小作為優化目標。

折疊椅骨架主要由截面尺寸為38×18mm，壁厚為0.9mm的空心方管和外徑為11mm，壁厚為1.1mm的空心圓管組成，選取空心方管的壁厚W1，空心圓管外徑D1和空心圓管壁厚T1作為設計變量。設定空心方管壁厚變化范圍為0.4mm～1mm，空心圓管外徑變換范圍為12mm～40mm，空心圓管壁厚變化范圍為0.6mm～3mm。

約束條件選取折疊椅骨架最大等效應力小于折疊椅許用應力，折疊椅骨架最大變形小于許用變形δ，其中δ=50mm。

折疊椅輕量化設計的數學模型為：

利用Isight集成ANSYS，在Isight中設定好參數，利用全局優化算法[10]進行優化計算，優化迭代1 001次，完成優化計算，表1為優化前后各設計變量數值。圖6為優化計算目標函數迭代曲線。優化后折疊椅骨架質量為5.88 kg，優化前折疊椅骨架質量為11.36 kg，通過優化設計折疊椅骨架質量減輕48.24%，達到輕量化設計要求。

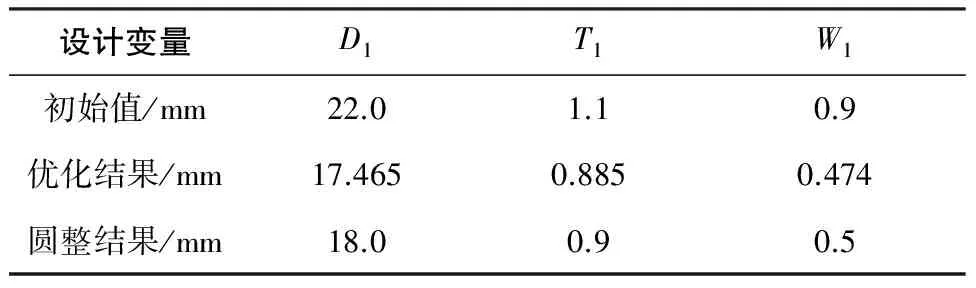
表1 優化前后各設計變量數值

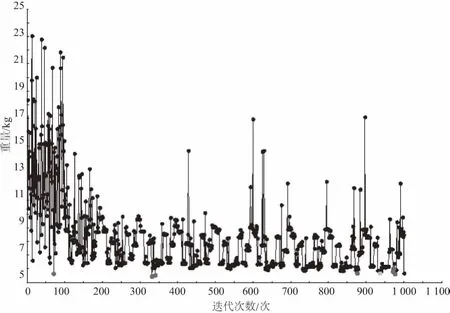
圖6 目標函數迭代曲線

考慮加工工藝以及加工成本的需要，按圓整優化后各設計變量結果重建折疊椅有限元模型，得到圓整后折疊椅骨架質量為6.73kg，比優化前質量減輕40%。再次進行折疊椅有限元計算，得到優化后折疊椅有限元模型的應力云圖和變形云圖如圖7和圖8所示。其中折疊椅的最大等效應力為263.73MPa，小于折疊椅許用應力，最大變形為13mm小于許用變形值，說明優化后折疊椅結構滿足強度、剛度要求，本次優化設計是可行的。

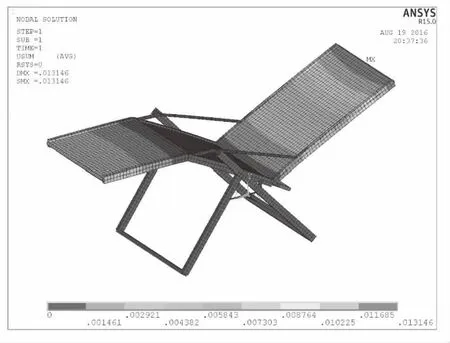
圖7 優化后折疊椅應力云圖

4 結語

1) 建立折疊椅的有限元模型，應用有限元分析方法

獲得折疊椅在極限姿態下的應力分布情況，在此基礎上，以折疊椅主要構件的截面尺寸為設計變量，以強度、剛度為約束條件，以折疊椅質量最輕為優化目標，對其進行尺寸優化設計，優化后折疊椅的質量減輕了40%，達到了輕量化的優化目標。

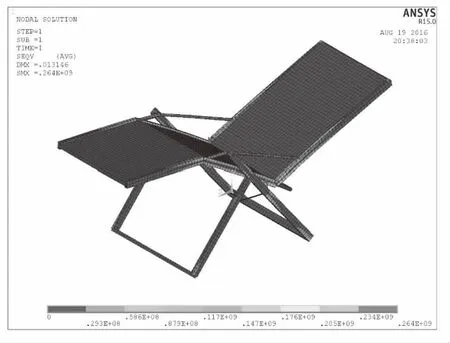
圖8 優化后折疊椅變形云圖

2) 提供了一種基于梁、板殼單元的折疊椅有限元建模方法，相比單利用殼體單元建模，增加折疊椅在較大的維度和方向上尋優，使得輕量化效果更為明顯。

3) 為折疊椅結構改進提供了一種行之有效的優化方法。

參考文獻:

[1] 馬驪溟，朱智民，李偉光，等. 滿意度動態加權法在自卸車車架拓撲優化中的應用[J]. 解放軍理工大學學報(自然科學版)，2013，14(4)：436-440.

[2] 張君媛，徐婷婷，張秋實,等. 長纖維復合材料乘用車后排座椅骨架輕量化設計[J]. 汽車技術，2015(8)：10-13.

[3] 張坤，丁曉紅，倪維宇,等. 汽車座椅骨架構件布局設計方法[J]. 工程設計學報，2015(2)：166-171.

[4] 賀巖松，黃深榮，張志飛,等. 摩托車車架基于梁單元的結構優化[J]. 機械科學與技術，2013，32(12)：1748-1751.

[5] 哈斯巴根，朱凌，石琴,等. 輪胎有限元建模過程優化及剛度特性仿真研究[J]. 合肥工業大學學報(自然科學版)，2015(7)：944-948.

[6] 劉照麟. 基于梁單元重要性的桿件結構優化方法及應用研究[D]. 桂林：桂林電子科技大學，2014.

[7] 趙韓，錢德猛. 基于ANSYS的汽車結構輕量化設計[J]. 農業機械學報，2005，36(6)：12-15.

[8] 唐進元,蒲太平. 基于有限元法的螺旋錐齒輪嚙合剛度計算[J]. 機械工程學報，2011，47(11)：23-29.

[9] 劉鴻文. 材料力學[M]. 北京：高等教育出版社，2004.

[10] 韓志強. 某發射裝置上架的減重技術研究[D]. 南京：南京理工大學，2006.