考慮DG隨機性的配電網電壓質量概率評估方法*

楊 夏，羿應棋，陶飛達，李桂昌，黃智鵬

0 引言

DG接入配電網后，徹底改變了配電網的結構，使配電網從單電源輻射狀結構變為遍布電源的復雜結構，其將對配電網的無功電壓特性產生重大影響[1-3]。以風電、光伏為代表的分布式新能源接入不僅改變了傳統配電網能量單向流通的特性，且因其發電的間歇性、波動性和不確定性使得電壓波動更顯劇烈，進而對配電網的電壓質量帶來很大的挑戰，嚴重威脅著用電設備的安全運行和敏感工業的安全生產[4-5]。

關于DG接入對配電網電壓質量的影響評估研究，文獻[6]利用剛性率和短路比評估了DG對配電網供電電壓質量的影響，得出在同等滲透率下，逆變型DG更加適合應用于密集負荷、高短路容量的城市配電網。文獻[7]針對不同類型的DG，采用系統電壓改善程度和有功網損改善程度兩個指標來評估不同類型DG對系統電壓和網損的影響程度。文獻[8]基于雙母線模型，分析了DG接入配電網對電壓分布的影響，提出了低壓母線注入電流的門檻值概念，并分析了影響該門檻值的各項參數，但是并沒有給出具有多個負荷節點的放射狀鏈式配電網絡節點電壓分布的一般表達式，而且只適合于單個DG的情況。文獻[9]給出了一種含DG的三角形負荷分布模型，并且根據電路疊加定理提出了基于此模型的電壓分布計算方法，并得出一定容量的DG接入配電網絡會對饋線上的電壓分布產生重大影響，影響程度與DG總容量的大小、接入位置有很大的關系；同時DG是否具有電壓調節作用與DG的類型、容量等有關，因此要根據實際運行狀況確定具體的調壓方案。文獻[10]講到DG最大允許接入容量主要是受到三種因素的制約，有故障等級因素、發熱限制以及電壓限制，并且在含DG的配電網中采用了三種極限狀況對其進行分析，分別是無DG接入但是接有最大負載、最大容量DG接入并且接有最大負載以及最大DG接入并且接有最小負載的情況。

總體上，大規模DG的接入會對原有的配電網電壓控制方面帶來重大的挑戰，需要在電網規劃階段就采取一些針對性的策略，并研究相應的運行控制方法[11-13]。基于此，本文以分布式光伏為主要研究對象，通過對其進行概率建模，并采用基于半不變量的概率潮流的計算方法，從概率學的角度研究高滲透率光伏接入對電網電壓的影響機理，對南方電網10 kV架空線路基態模型進行仿真計算與分析，表明所提評估方法具有較好的實用性。

1 半不變量的概念與求解

1.1 半不變量基本概念

隨機變量的分布特性可以根據其數字特征進行描述，半不變量作為數字特征之一，可以方便且準確地刻畫隨機變量的分布情況。

假設F(x)是隨機變量X的累積分布函數，令t為任意一實數，則函數g(x)=ejtx=cos(tx)+jsin(tx)在(-∞，+∞)上關于F(x)的積分稱為F(x)的特征函數，即：

將F(x)的特征函數取對數并在t=0處展開為麥克勞林級數，整理得：

其中γk就是半不變量，又稱累積量，下標k表示半不變量的階數。

1.2 半不變量求解方法

半不變量的求解主要通過數值解析和蒙特卡洛兩種方法實現，其中數值解析法指的是當隨機變量分布情況已知時，根據具體分布的數字特征，通過數學公式推導計算得到其各階半不變量；如果隨機變量分布情況未知，或分布情況較為復雜，難以用數值解析法求解，可通過蒙特卡洛抽樣計算得到其各階半不變量[14-15]。

采用蒙特卡洛法求解時，先計算隨機變量的矩特征，再計算其半不變量，即：

其中，αk表示隨機變量的k階原點矩；xsi表示隨機變量的數據樣本中第i個數據點；n表示數據樣本容量；Cik-1表示從(k-1)個不同元素中取出i個元素的組合，其中滿足i≤k-1。

2 Gram-Charlier級數展開

Gram-Charlier級數展開是一種根據隨機變量的各階半不變量近似求解得到該隨機變量的概率密度函數和累積分布函數的級數展開方法，其是基于標準正態分布函數拓展得到的。因此，該方法需先對隨機變量及其各階半不變量進行標準化，進而求解得到標準化后隨機變量的概率分布函數，最后進行標準化還原以得到標準化前隨機變量的概率分布函數。

假定隨機變量X的期望值為μX、標準差為σX，由Xˉ=(X-μX)/σX計算得到標準化后的隨機變量。根據A型Gram-Charlier級數展開式可計算得到標準化隨機變量Xˉ的概率密度函數和累積分布函數，即：

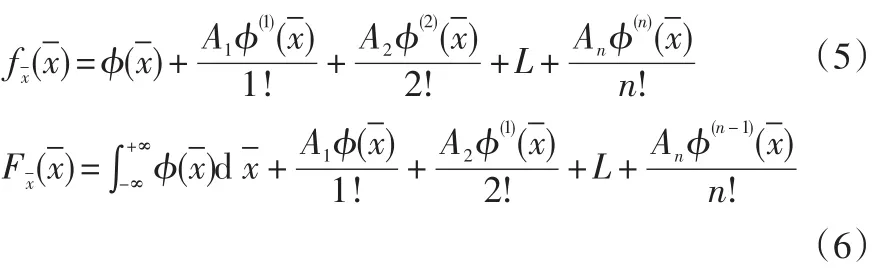
其中，Φ(·)表示服從標準正態分布隨機變量的概率密度函數；Φ(n)(·)表示Φ(·)n階求導的結果；A1，A2，….，An表示Gram-Charlier級數展開的各項系數，可根據式（7）計算得到：

其中，γ(k)Xˉ表示標準化隨機變量Xˉ的k階半不變量。

3 光伏和負荷的概率建模

3.1 光伏概率建模

相關文獻研究表明，在短時間尺度上，太陽能光照強度的隨機變化服從Beta分布[16]，即：

其中，fR(·)表示光照強度隨機變量R的概率密度函數；r和rmax分別表示該時段內光照強度的實際值和最大值；Γ(·)表示Gamma函數；α和β分別表示Beta分布的兩個形狀參數，具體可根據式（9）計算得到：

當已知太陽能光照強度分布情況時，近似認為光伏輸出有功功率和光照強度呈線性關系，即：

其中，PPV為該時段內光伏輸出有功功率實際值；A為光伏電池板的總面積；η為光電轉換效率。

3.2 負荷概率建模

經大量研究表明，配電網負荷有功功率近似服從正態分布，并假定按恒功率因數運行，則無功功率也服從正態分布。因此，負荷的概率模型為：

4 考慮光伏空間相關性的電壓質量概率評估

4.1 光伏出力相關性解耦方法

基于半不變量的概率潮流計算需滿足輸入隨機變量相互獨立的前提，否則將不再適用。因此，本文首先提出了一種基于TPNT的Nataf變換方法，用于輸入隨機變量相關性解耦處理；再通過Nataf逆變換產生滿足預先設定的相關性水平的各光伏出力數據樣本，以便后續處理[17-18]。

（1）Nataf變換

目前常用于描述隨機變量相關性的方法是相關系數矩陣法，假設隨機變量空間X是一個n維向量X=(X1，X2，L，Xn)，定義一個相關系數矩陣ρX用于描述各變量之間的相關性：

Nataf變換指的是先將具有相關性的待求隨機變量空間X映射至具有相關性的服從標準正態分布的隨機變量空間Y，再映射至獨立的服從標準正態分布隨機變量空間Z的變換方法。

第一步映射滿足等概率轉換原則，如式(14)所示，再根據式(15)計算得到隨機變量空間Y的相關系數矩陣ρY。

其中，FXi(xi)表示隨機變量xi的邊緣分布函數；Φ(·)、φ(·)分別表示標準正態分布的概率密度函數和累積分布函數；ρxiy和ρyiy分別表示隨機變量X和Y對應的相關系數矩陣第i行第j列的元素。

第二步映射需通過Cholesky因式分解實現。首先根據式（16）對相關系數矩陣進行Cholesky因式分解，再通過式（17）計算得到隨機變量空間Z：

其中，D即為Cholesky因式分解所得的下三角矩陣；D-1指D的逆。

（2）TPNT理論

前面闡述了利用Nataf變換解耦相關性的理論方法，但是根據式(14)求解ρY時，計算復雜，難以求解。本章節介紹了一種三階多項式正交變換方法(TPNT)簡化ρY的求解計算。

根據TPNT理論，具有相關性的隨機變量空間X可由獨立的服從標準正態分布隨機變量空間Z的三階多項式表示，具體如式(18)：

將隨機變量xi進行標準化，則有：

顯然，各項系數ai(k)和bi(k)之間關系滿足∶

根據矩法原理，式(20)中等式兩邊的各階原點矩相等，展開可得：

其中，χ表示變量xi_st的偏度，κ表示變量xi_st的峰度。

利用非線性方程組求解方法對式（21）計算可得bi(k)，再根據式（20）求得ai(k)，最后可計算得到具有相關性的服從標準正態分布的隨機變量空間Y的相關系數矩陣ρY：

根據統計學相關理論可知，相關系數ρ應為區間[-1，1]內一實數，同時在上述進行空間映射時，相關系數也應為同號，即ρY須滿足：

至此，利用TPNT可較為簡便地求解得到隨機變量空間Y的相關系數ρY。

4.2 電壓質量概率評估流程

通過4.1節可實現光伏空間相關性解耦，確保節點注入功率相互獨立，從而可利用前述的基于半不變量概率潮流計算方法進行求解，并根據建立的評估指標進行電壓質量概率評估，具體計算步驟如下所示：

1）輸入原始數據；

2）構建配電網負荷和分布式光伏的概率模型；

3）設置各光伏電源之間的相關系數矩陣ρPV，并根據式（18）～（23）計算得到具有相關性的服從標準正態分布隨機變量空間Y的相關系數矩陣ρY；

4）根據式（16）對進行Cholesky因式分解，計算得到下三角矩陣D；

5）設置樣本容量m，構建獨立的服從標準正態分布隨機變量空間Z的數據樣本，并利用Y=DZ計算得到具有相關性的服從標準正態分布隨機變量空間Y的數據樣本；

6）利用等概率轉換公式ρPVi=F-1PVi(Φ(yi))(i=1，2，L，n)（其中n為系統接入光伏的數量）計算得到滿足相關系數矩陣ρPV的各光伏電源有功出力的數據樣本，完成Nataf逆變換；

7）利用Cholesky分解將相關性隨機變量的各階半不變量轉換成不相關的各階半不變量；

8）修改交流潮流模型的靈敏度矩陣，此時，節點注入功率相互獨立，滿足半不變量法概率潮流計算的應用前提，利用半不變量法概率潮流計算并結合Gram-Charlier級數展開式求得節點電壓U和支路功率Z的概率密度函數和累積分布函數，并根據評估指標進行電壓質量概率評估。

5 仿真算例

5.1 模型簡介

圖1 仿真模型

圖2 光照強度Beta分布的概率分布曲線

基于MATLAB平臺進行編程仿真，選取前述的南方電網10 kV配電網架空線基態模型作為仿真算例，如圖1所示。負荷期望值取基準運行點下參數，標準差取為期望值的10%。在節點94、95和96接入分布式光伏，功率因數均取為0.99。計算節點電壓越限概率時，電壓概率合格區間設置為[0.95，1.05]，根據歐洲標準EN50160規定配電網電壓越限概率應小于某一給定值，本報告將該給定值設為5%，即當電壓越限概率大于5%時，配電網存在電壓安全風險。計算節點電壓置信區間時，置信度取為0.9。

利用HOMER軟件獲取GMT+08∶00時區中國廣州市(23°6′N，113°2′E)七月份 13∶00 時刻的光照強度模擬時序，假定光照強度月特性服從Beta分布，數據擬合得形狀參數α為1.6841，β為1.164，其概率分布情況如圖2所示。

如表1所示，仿真模型設置了10%（低滲透比）、50%（中滲透比）、100%（高滲透比）三種滲透比水平，其余光伏參數請詳見表中。

表1 不同滲透比水平下分布式光伏參數表

5.2 仿真結果

當分布式光伏空間相互獨立時，0滲透比、低滲透比、中滲透比和高滲透比四種場景下，仿真所得光伏并網點電壓質量概率評估結果如表2、表3所示，光伏并網節點32電壓概率密度曲線和累積分布曲線如圖3、圖4所示，不同滲透率水平下系統節點電壓期望值對比如圖5所示。

表2 不同滲透比水平下光伏并網點電壓置信區間

表3 不同滲透比下系統電壓平均越限概率和最大越限概率

圖3 不同滲透比下光伏并網節點32電壓概率密度曲線對比

圖4 不同滲透比下光伏并網節點32電壓累積分布曲線對比

圖5 不同滲透比水平下節點電壓期望值對比

分析以上圖表可得以下結論：

（1）由圖3、圖4可見，隨著光伏滲透比逐漸增加，光伏并網節點32電壓明顯升高，同時波動性也逐漸增大。當滲透比高達至100%時，節點32電壓置信區間為[1.037，1.080]，電壓水平越上限，波動程度大；

（2）由表2可見，當光伏滲透比由0增加至100%時，光伏并網節點32電壓置信區間寬度從0.007增加至0.043，置信區間下限從0.976增加至1.036，增加幅度為6.15%，置信區間上限從0.983增加至1.080，增加幅度為9.87%，說明了光伏滲透比增加使節點電壓期望值抬升的同時，明顯增加了電壓波動上限，增加了電壓越限風險；

（3）由表3可知，由于線路模型參數問題，滲透比為0、10%和50%情況下均未出現電壓越限現象，當滲透比高達100%時，系統電壓越上限程度明顯，節點32電壓越限概率最大，為78.98%；

（4）由圖5可知，隨著滲透比逐漸升高，節點電壓期望值均明顯升高，當滲透比為100%時，系統電壓期望值僅為1.06 p.u.，但系統卻存在明顯的電壓越限風險，說明了考慮光伏隨機性對配電網電壓質量準確評估具有重要意義。

6 結語

本文針對分布式光伏出力間歇性、隨機性明顯的特征，引入了概率潮流理論進行含分布式光伏配電網電壓質量的概率評估。首先提出了一種基于半不變量的概率潮流計算方法，構建了負荷和光伏的概率模型，并提出了節點電壓置信區間、系統電壓平均越限概率和最大越限概率三個指標來進行電壓質量概率評估；最后，提出了一種計及光伏空間相關性的概率潮流計算方法進行了配網動態概率潮流計算。算例仿真表明，準確考量光伏的空間相關性和時序特性，才能準確可靠地評估光伏接入對系統電壓安全性的影響，對系統的規劃運行具有重大意義。

參考文獻：

［1］周辛南，柯德平，孫元章.基于配電網靜態電壓質量機會性約束的可再生能源分布式發電容量規劃［J］.電力自動化設備，2015，35（09）：143-149.

［2］張瑋亞，李永麗.面向多分布式電源的微電網分區電壓質量控制［J］.中國電機工程學報，2014，34（28）：4827-4838.

［3］趙憲，周力行，熊家偉，等.含分布式電源配電網電壓質量綜合評估［J］.電力科學與技術學報，2013，28（04）：49-53.

［4］葉萌，劉文霞，張鑫.考慮電壓質量的分布式電源選址定容［J］.現代電力，2010，27（04）：30-34.

［5］羅家健.配電網電壓偏差綜合優化案例分析［J］.機電工程技術，2013，42（04）：31-36.

［6］裴瑋，盛鹍，孔力，等.分布式電源對配網供電電壓質量的影響與改善［J］.中國電機工程學報，2008（13）：152-157.

［7］張立梅，唐巍，趙云軍，等.分布式發電接入配電網后對系統電壓及損耗的影響分析［J］.電力系統保護與控制，2011，39（05）：91-96.

［8］Conti S，RaitiS，TinaG.Small-scale Embedded Genera?tion Effect on Voltage Profile：An analytical Method［J］.IEE Proceedings-Generation and Transmission and Distribution，2003，150 （1）：77-86.

［9］陳芳，王瑋，徐麗杰，等.分布式電源接入對配電網電伍變化的分析［J］.電力系統及其自動化學報，2012 （04）：145-149.

［10］ Ferry August Vlawan.Voltage Control and Voltage Sta?bility of Power Distribution System in the Presence of Distributed Generation ［D］.Gothenburg： Chalmers University of Technology，2008.

［11］劉健，張志華，黃煒，等.分布式電源接入對配電網故障定位及電壓質量的影響分析［J］.電力建設，2015，36（01）：115-121.

［12］徐俊俊，黃永紅，王琪，等.基于自然選擇粒子群算法的含DG接入的配電網無功優化［J］.電測與儀表，2014，51（10）：33-38.

［13］朱文軒.基于PSO算法的含DG配電網無功優化研究［D］.成都：西南交通大學，2013.

［14］郭效軍，蔡德福.不同級數展開的半不變量法概率潮流計算比較分析［J］.電力自動化設備，2013，33（12）：85-90.

［15］石東源，蔡德福，陳金富，等.計及輸入變量相關性的半不變量法概率潮流計算［J］.中國電機工程學報，2012，32（28）：104-113.

［16］陳旭，楊雨瑤，張勇軍，等.光伏光照概率性對配電網電壓的影響［J］.華南理工大學學報（自然科學版），2015，43（04）：112-118.

［17］陳璨，吳文傳，張伯明，等.考慮光伏出力相關性的配電網概率潮流［J］.電力系統自動化，2015，39（09）：41-47.

［18］高英，謝開貴，胡博，等.考慮光伏出力與負荷相關性的光伏電站容量可信度評估［J］.電力系統保護與控制，2013，41（14）：1-6.