ON A CLASS OF DOUGLAS FINSLER METRICS?

Hongmei ZHU(朱紅梅)

College of Mathematics and Information Science,Henan Normal University,Xinxiang 453007,China

E-mail:zhm403@163.com

1 Introduction

In Finsler geometry,Douglas curvature is an important projectively invariant,which is introduced by J.Douglas in 1927.It it also a non-Riemannian quantity,because all the Riemannian metrics have vanishing Douglas curvature inherently.Finsler metrics with vanishing Douglas curvature are called Douglas metrics.Roughly speaking,a Douglas metric is a Finsler metric which is locally projectively equivalent to a Riemannian metric[5].

Douglas metrics form a rich class of Finsler metrics including locally projectively flat Finsler metrics[4]and Berwald metrics;The later are those metrics which Berwald curvatures vanish[1].It is known that a Finsler metric is locally projectively flat,namely,its geodesics are all straight line segments in some suitable locally coordinate system,if and only if its both Douglas curvature and Weyl curvature vanish.

A Randers metric,introduced by a physicist G.Randers in 1941,is of the form F=α+β,whereis a Riemannian metric and β=bi(x)yiis a 1-form.However,it can also be expressed in the following navigation form

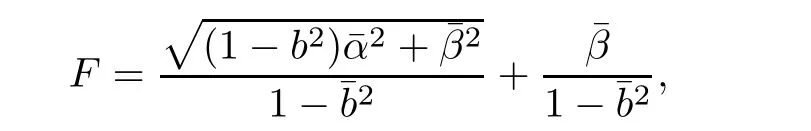
(α,β)-metrics are a rich and important class of Finsler metrics,partly because they are“computable”.The researches on(α,β)-metrics enrich Finsler geometry and the approaches offer references for further study.In 2009,B.Li,Y.Shen,and Z.Shen gave a characterization of Douglas(α,β)-metrics with dimension n ≥ 3[5].

A more general class named general(α,β)-metric was first introduced in[11]in the following form

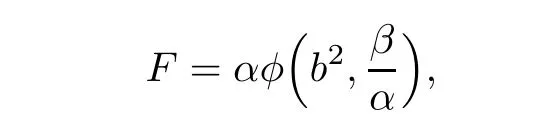
where α is a Riemannian metric,β is a 1-form,b:= ‖βx‖α,and φ(b2,s)is a smooth function.If φ = φ(s)is independent of b2,then F=is an(α,β)-metric.If α =|y|, β = 〈x,y〉,thenis the so-called spherically symmetric Finsler metrics[9,13,15].Moreover,general(α,β)-metrics include part of Bryant’s metrics[2,11]and part of fourth root metrics[7].In[9],X.Mo,N.M.Solórzano,and K.Tenenblat determined all of spherically symmetric Douglas Finsler metrics.Under the condition that β is closed and conformal,the author determined all of Douglas general(α,β)-metric[14].

In this article,we only need the condition that β is not parallel with respect to α determines all of Douglas general(α,β)-metric on a manifold of dimension n ＞ 2.The main result is given below.

Theorem 1.1Let F= αφ(b2,s),s=,be a regular general(α,β)-metric on an open subset U ? Rn(n ≥ 3).Suppose that β is not parallel with respect to α and F is not of Randers type.Then,F is a Douglas metric if and only if F lies in one of the following cases:

(1)φ=φ(b2,s)satisfies

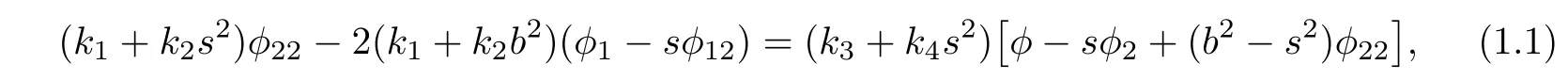
where ki:=ki(b2),i=1,2,3,4 and β satisfies

where τ= τ(x)is a scalar function on U.

(2)φ=φ(b2,s)satisfies(1.1)and

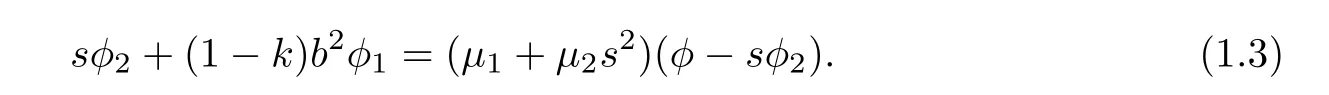
Moreover,β satisfies

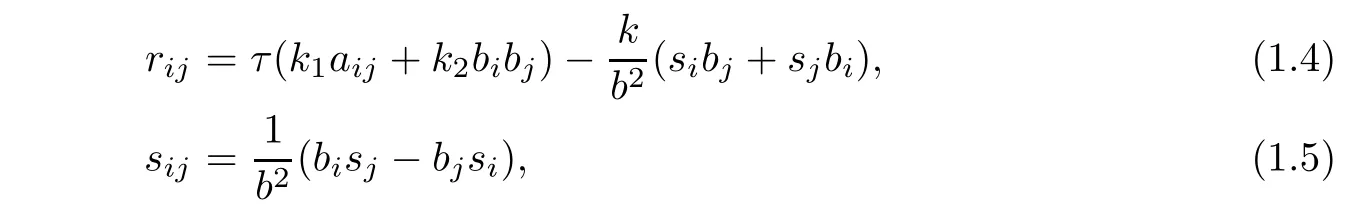
where k:=k(b2)/=1,μi:=μi(b2),i=1,2 andμ1+μ2b2=(k+1).In this case,dβ /=0.

(3)φ=φ(b2,s)satisfies(1.1)and

Moreover,β satisfies

Let us take a look at a special case;When φ1=0,takingthe case 1 of Theorem 1.1 is reduced to a result which characterizes Douglas(α,β)-metrics with dimension n ≥ 3(Theorem 1.1 in[5]).Notice that Theorem 1.1 contains some important singular,Finsler metrics,for example Finsler metrics of Kropina type.

X.Wang and B.Li studied Douglas general(α,β)-metrics in[10].Their result is just case 1 of Theorem 1.1.However,we find that case 2 and case 3 also exist recently.For example,for case 2,takeand k=3,then in this case,(1.1)and(1.3)are reduced to the followings:

By a direct computation,it is easy to verify that the following function

satisfies(1.8)and(1.9),where f(t)is an arbitrary function satisfying the following inequalities:

In this case,the corresponding general(α,β)-metric is a regular Finsler metric.

In the following,according to(1.10),for case 2,let us take a look at an example.

Example 1.1Let M be a manifold of dimension n ＞ 2.TakeandIt is easy to verify that α and β satisfy

Moreover,dβ/=0.Choose f=(t+2)2in(1.10),then

where b:= ‖β‖α=Hence,the corresponding Finsler metrics

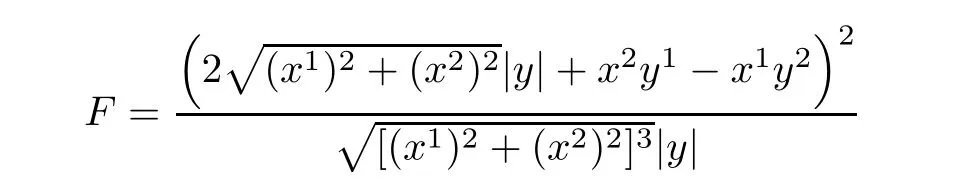
are Douglas metrics.

Similarly,we can find regular Finsler metrics in case 3.Mostly important,β is closed in the case of(α,β)-metrics;However,it is seen from Theorem 1.1 that β permits not closed in the case of general(α,β)-metrics.That is to say,our results express that Douglas general(α,β)-metrics are much more and richer than Douglas(α,β)-metrics.

For three cases of Theorem 1.1,it is easier to solve case 1 because it is close to the result of Douglas(α,β)-metrics.However,case 2 and case 3 do not occur in the case of Douglas(α,β)-metrics,especially β is not closed.It is a pleasure and surprised to us.The two cases are complicated.

2 Preliminaries

In local coordinates,the geodesics of a Finsler metric F=F(x,y)are characterized by

where

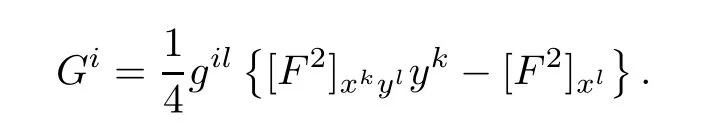
The local function Gi=Gi(x,y)define a global vector fieldon TM{0},which is called the spray.For a Riemannian metric,the spray coefficients are determined by its Christoffel symbols as

Douglas metrics can be characterized by

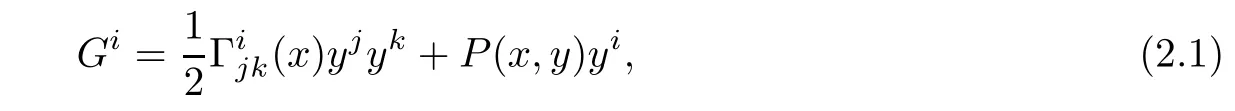
It is known that Douglas metrics can be also characterized by the following equations[1]

By definition,a general(α,β)-metric is a Finsler metric expressed in the following form,

where φ(b2,s)is a positive smooth function defined on the domain|s|≤ b ＜ bofor some positive number(maybe in finity)bo.Then,the function F= αφ(b2,s)is a Finsler metric for any Riemannian metric α and any 1-form β if and only if φ(b2,s)satisfies

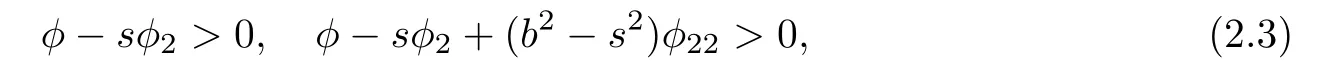
when n≥3 or

when n=2[11].

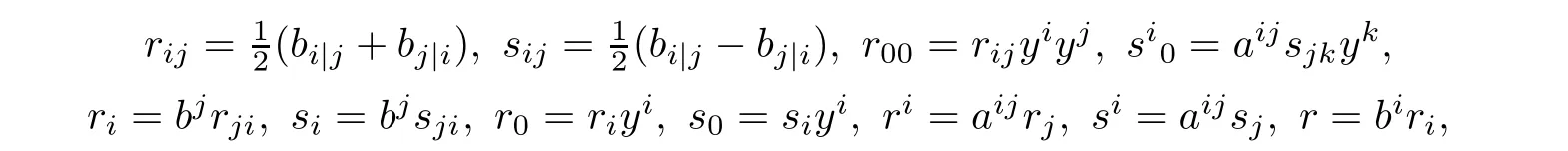
where(aij):=(aij)?1and bi:=aijbj.It is easy to see that β is closed if and only if sij=0.

According to[11],the spray coefficients Giof a general(α,β)-metricare related to the spray coefficientsαGiof α and given by

where

3 Necessary Conditions

In this section,we are going to show the necessary conditions for a general(α,β)-metric to be a Douglas metric.

Lemma 3.1Let F= αφ(b2,s),s=be a regular general(α,β)-metric on an open subset U ? Rn(n ≥ 3).Suppose that β is not parallel with respect to α and F is not of Randers type.If F is a Douglas metric,then F lies in one of the following cases:

(1)φ=φ(b2,s)satisfies

where ki:=ki(b2),i=1,2,3,4 and β satisfies

where τ= τ(x)is a scalar function on U.

(2)φ=φ(b2,s)satisfies(3.1)and

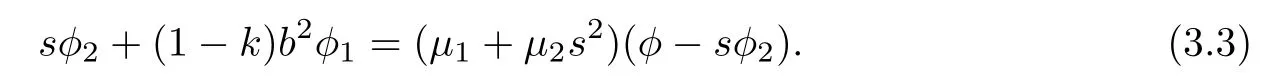
Moreover,β satisfies

Moreover,β satisfies

where θ:= θiyiis a 1-form which is perpendicular to β. ξi:= ξi(b2),i=1,2 and

ProofBy(2.2)and(2.5),we can show that a general(α,β)-metric is a Douglas metric if and only if

To simplify the computations,we take the following coordinate transformation:(s,ua)→(yi)by

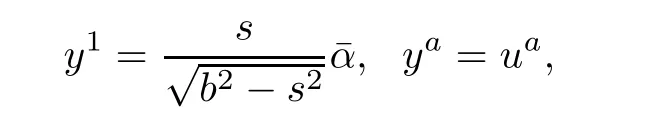
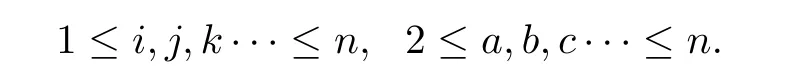
Then,

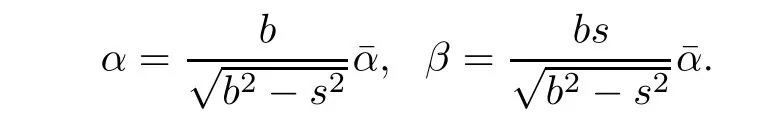
Let

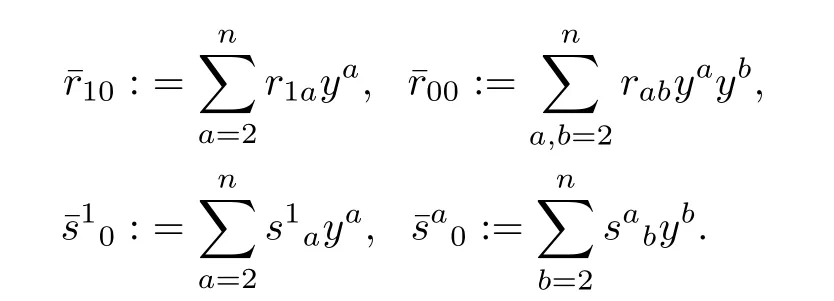
Because expression(3.8)involves rij,sijetc,one needs the following expression:

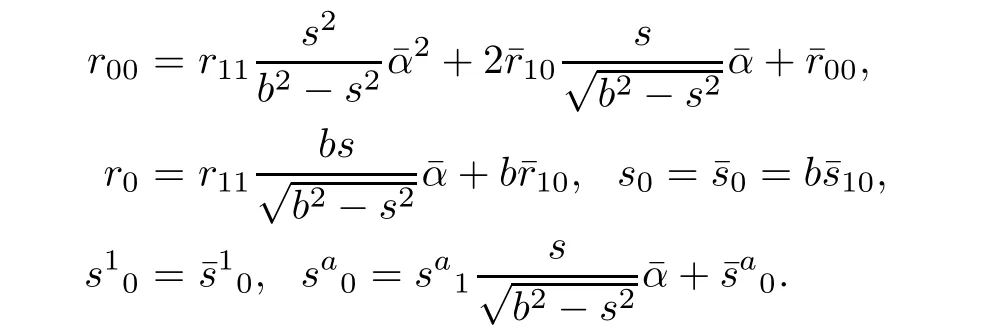
Note that s1=bs11=0.Plugging the above identities into(3.8),we get a system of equations in the following form

where Aijand Bijare polynomials in ya.We must have

Let

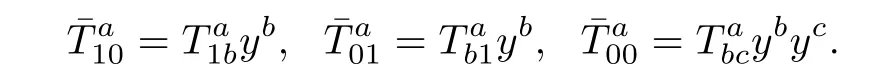
For i=1,j=a,by(3.8),we get

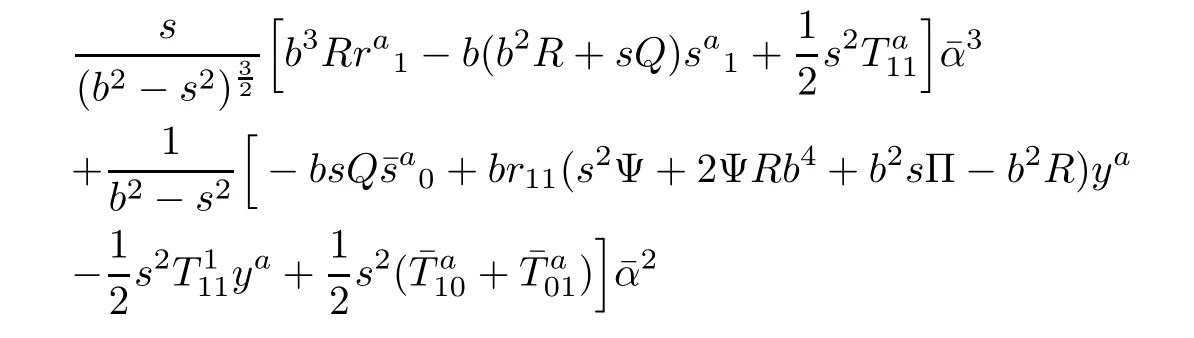
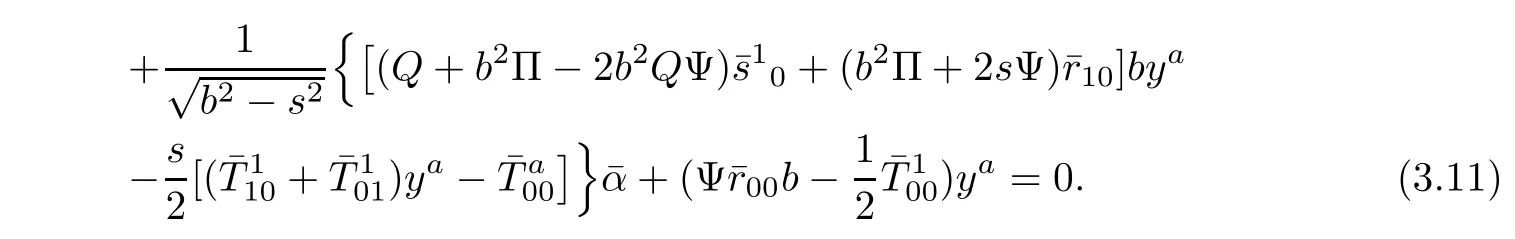
From(3.9)and(3.10),then(3.11)is equivalent to

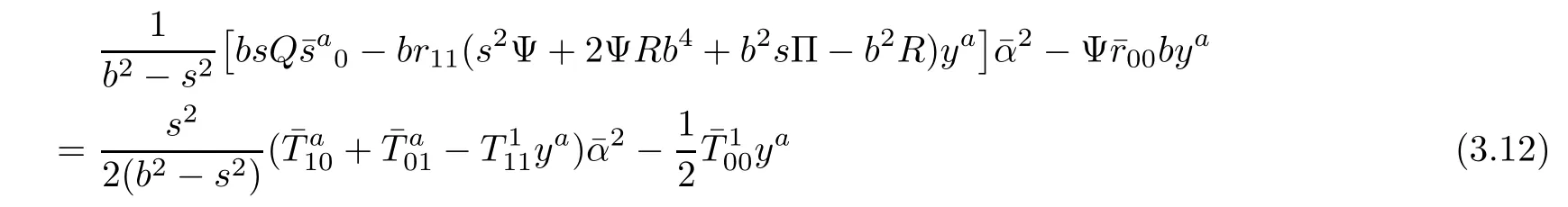
and

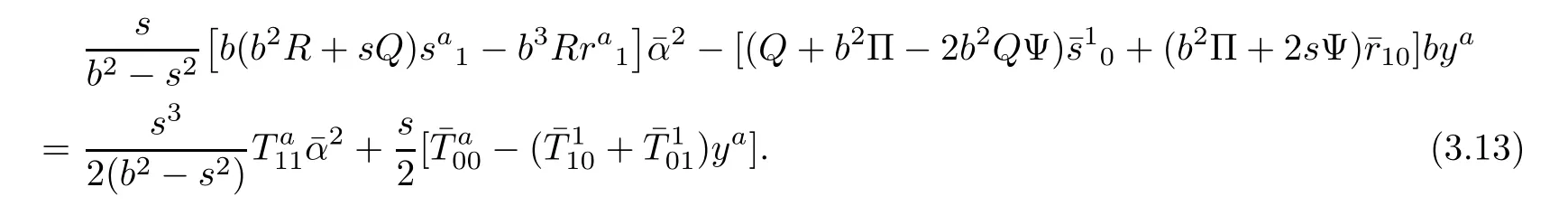
For i=a,j=b,by(3.8)we get

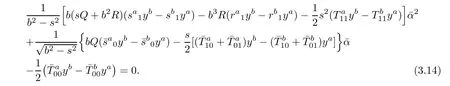
It follows from(3.9)and(3.10)that(3.14)is equivalent to

and

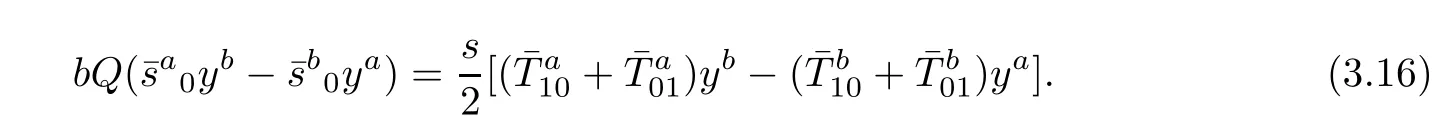
Let

Then,(3.16)can be rewritten as

By(3.17),it is easy to show that

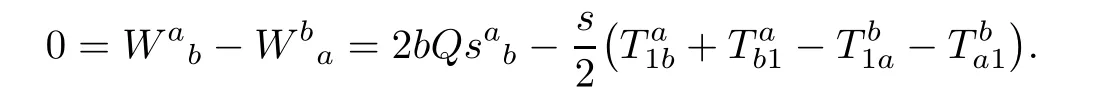
We also get

where

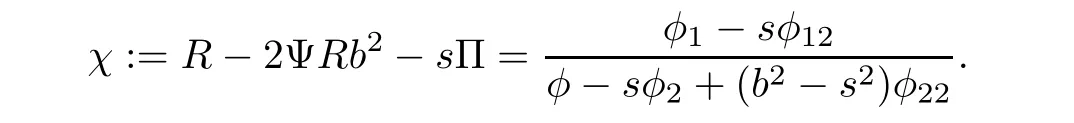
Taking s=b in(3.20),we find that the ratio of r11and?B is a function of b2.Hence,suppose thatplugging them into(3.20)yields

Let s=0,then(3.21)is reduced to

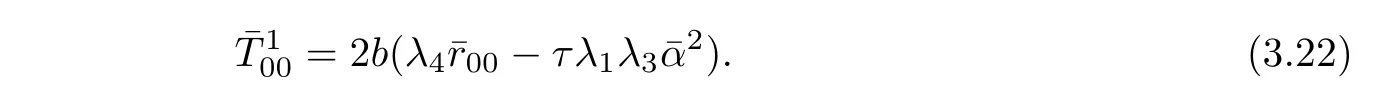
where λ3(b2)= χ(b2,0)and λ4(b2)= Ψ(b2,0).Plugging(3.22)into(3.21)yields

By(3.23),there exists a scalar function λ5(b2)such thatIn this case,(3.23)is reformed as

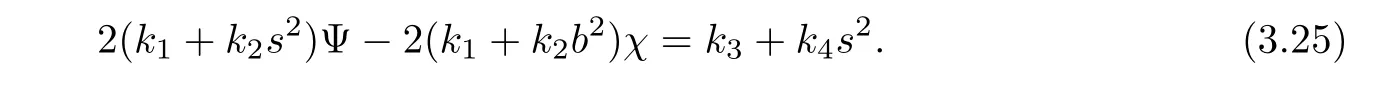
Inserting Ψ and χ into(3.25)yields

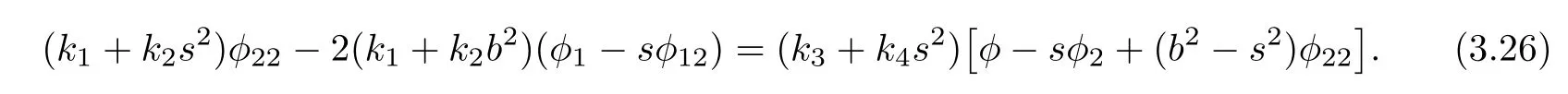
By now,we have obtained

Next,we are going to obtain ra1and sa1from(3.13)and(3.15).Let s=0 in(3.15),we obtain

where ε1= ε1(b2).Plugging(3.28)into(3.15)yields

Taking s=b in(3.29),we have

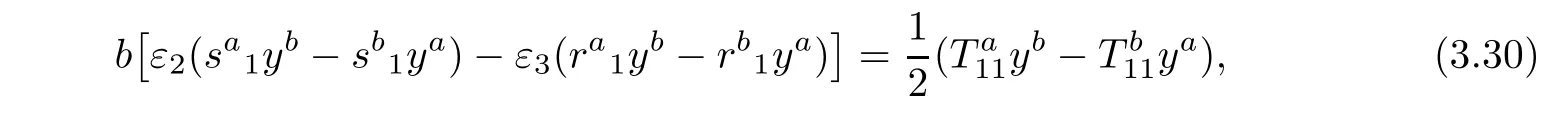
where ε2:= ε2(b2)and ε3:= ε3(b2).Inserting(3.30)into(3.29)yields

By(3.31),we divide the problem into three cases:

(1)ra1=0,sa1=0;

(2)ra1=k(b2)sa1,sa1/=0;

(3)sa1=0,ra1/=0.

Case 1ra1=0,sa1=0.

In this case,by(3.13)and(3.15),it is obtained thatBy sa1=0 and(3.18),then β is closed.From ra1=0 and(3.27),it follows that

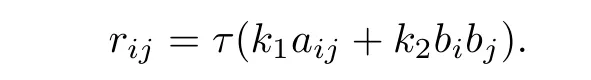
By the above equality and β being closed,we obtain(3.2).By(3.26),we obtain(3.1).

Case 2ra1=k(b2)sa1,sa1/=0.

Because sa1/=0,β is not closed.Moreover,we have obtained

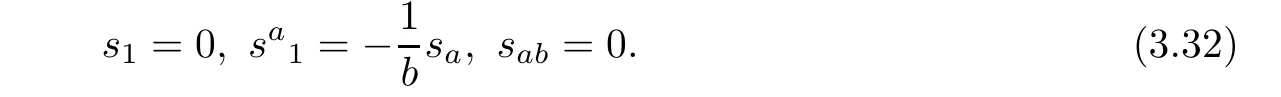
Noting that sijis skew symmetric,by(3.32),we obtain(3.5).In this case,ra1=?;Let us summarize what we have proved so far

By(3.33),we have(3.4).

By(3.31)and sa1/=0,we have

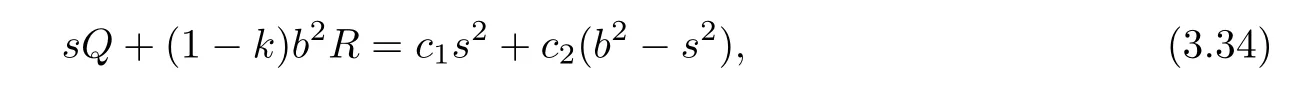
where c1= ε2?kε3and c2:=(1?k)ε1.From(3.34),we claim that k/=1.If k=1,then(3.34)is reduced to bQ=c1s.In this case,φ=1+c1bs2.Hence,F is Riemannian.Plugging Q and R into(3.34),we rewrite it as

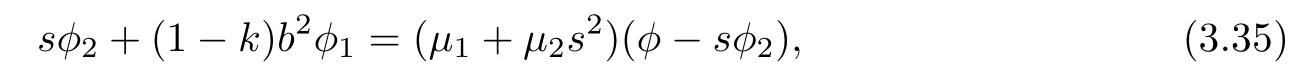
whereμ1:=c2b2,μ2:=c1?c2.

Differentiating(3.35)with respect to s yields

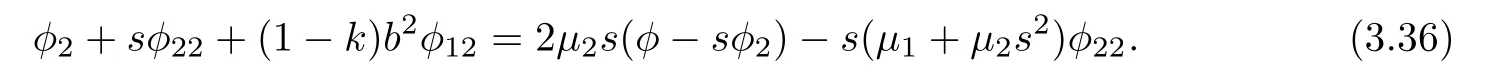
Contracting(3.13)with yayields

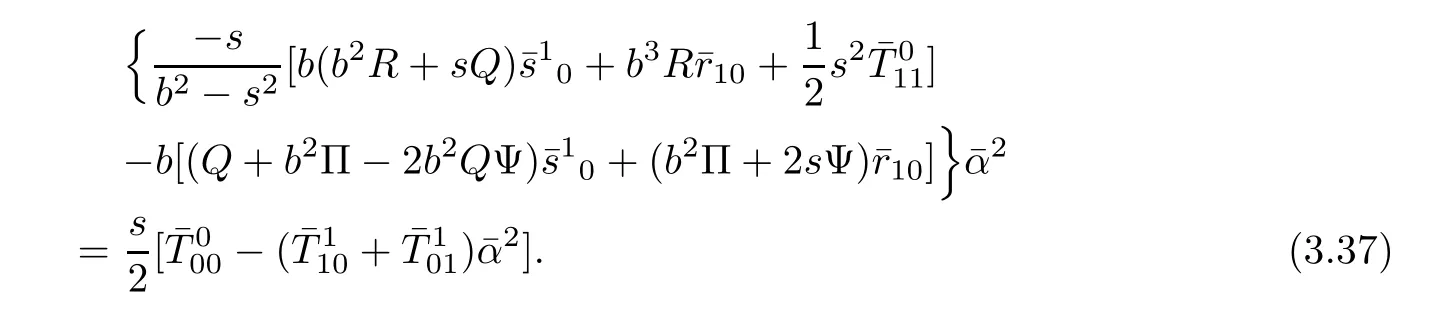
Plugging ra1=ksa1into(3.30)yields

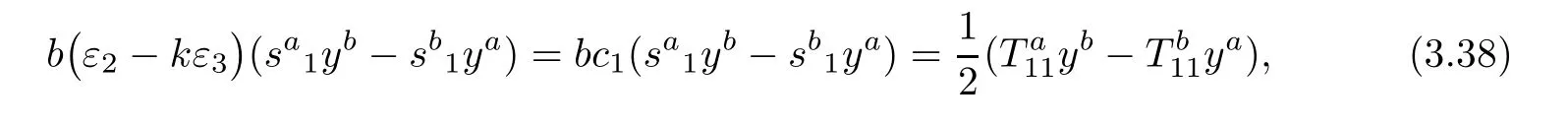
By(3.38),we get

Plugging ra1=ksa1and(3.39)into(3.37)yields

Because the coefficients of the right side in(3.40)is independent of s,if(3.40)holds,then by(3.34),we obtain

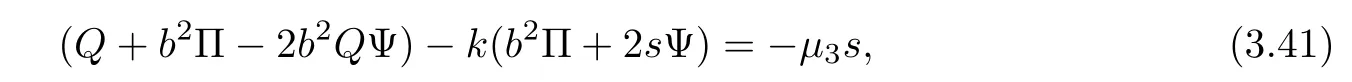
where μ3:=and λ3:= λ3(b2).

By making using of(3.35)and(3.36),we have

Plugging(3.42)into(3.41)yields

We claim that k+1+2μ1?μ3b2=0 and 2μ2+μ3=0.If k+1+2μ1?μ3b2/=0,by solving(3.43),we obtain

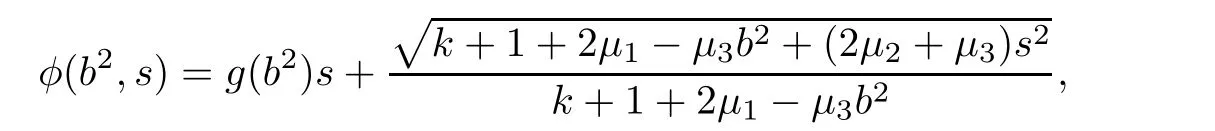
where g(b2)is an arbitrary smooth function.Hence,the corresponding general(α,β)-metric is of Randers type.This case is excluded in the assumption of Theorem 1.1.If k+1+2μ1?μ3b2=0 and 2μ2+μ3/=0,then we obtain

At this time,the corresponding general(α,β)-metric is of Kropina type.This case is excluded because this class of metrics are singular.Hence,

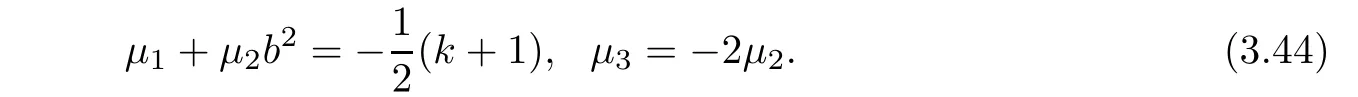
Case 3sa1=0,ra1/=0.

In this case,for rij,we have obtained

Therefore,by(3.45),we have

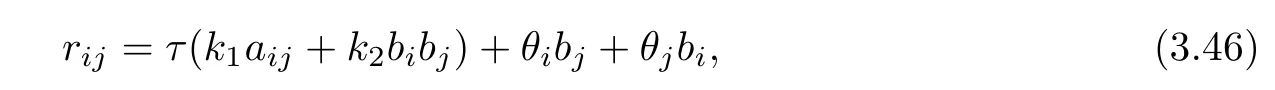
where θ := θiyiis a 1-form,which is perpendicular to β.By sa1=0 and(3.18),then β is closed.Hence,it follows from(3.46)that we obtain(3.7).

Because sa1=0 and ra1/=0,by(3.31),we obtain

Plugging R into(3.47)yields

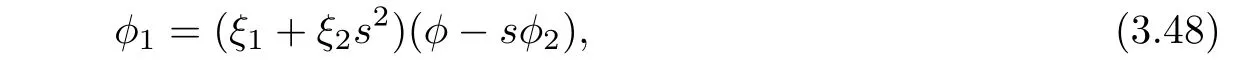
where ξ1:= ε1and.Differentiating(3.48)with respect to s yields

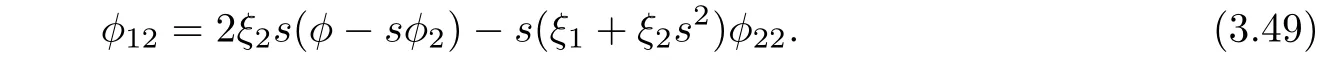
Plugging sa1=0 into(3.13)yields

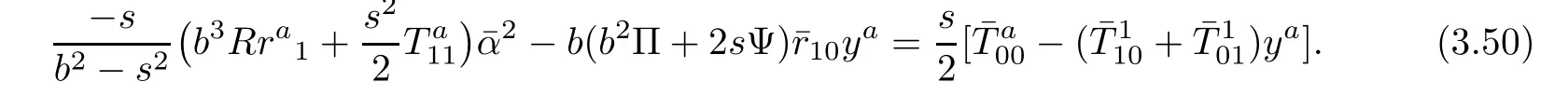
Contracting(3.50)with respect to yayields

Plugging sa1=0 into(3.30)yields

By(3.52),we conclude that

Plugging(3.53)into(3.51)yields

By(3.47),the above equality is reduced to the following

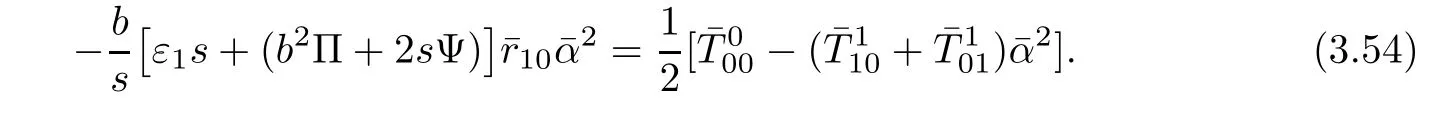
Because the right side in(3.54)is independent of s,there exists a function η(b2)such that

We rewrite(3.55)as

where ξ3:= η ? ε1.By(3.48)and(3.49),we obtain

Plugging(3.57)into(3.56)yields

We claim that 1?2b2ξ1?b2ξ3=0 and ξ3?2b2ξ2=0.If 1?2b2ξ1?b2ξ3/=0,then by solving(3.58),we obtain

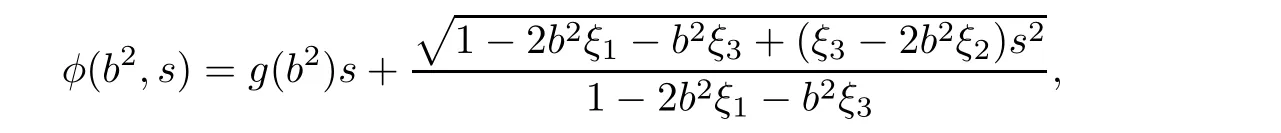
where g(b2)is an arbitrary smooth function.Hence,the corresponding general(α,β)-metric is of Randers type.This case is excluded in the assumption of Theorem 1.1.If 1?2b2ξ1?b2ξ3=0 and ξ3? 2b2ξ2/=0,then we obtain At this time,the corresponding general(α,β)-metric is of Kropina type.This case is excluded because this class of metrics are singular.Therefore,we obtain

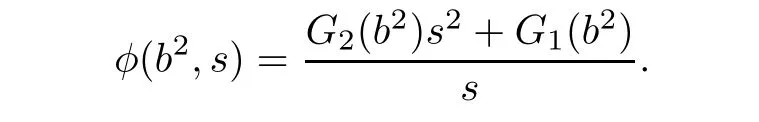
By(3.18),we have the following result.

Remark 3.1If a general(α,β)-metric is a Douglas metric,then the Rank of skew symmetric matrix(sij)is not greater than 2.

4 Sufficient Conditions

In this section,we show the sufficient conditions for a general(α,β)-metric to be a Douglas metric.

Lemma 4.1Let F= αφ(b2,s),s=,be a regular general(α,β)-metric on an open subset U ? Rn(n ≥ 3).Suppose that β is not parallel with respect to α and F is not of Randers type.Then,F is a Douglas metric if one of the following cases holds:

(1)φ=φ(b2,s)satisfies

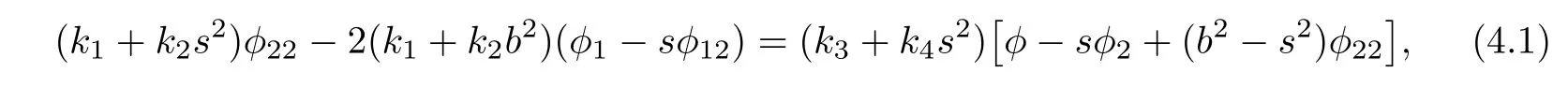
where ki:=ki(b2),i=1,2,3,4 and β satisfies

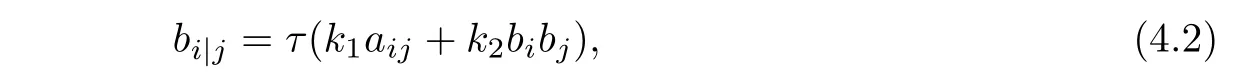
where τ= τ(x)is a scalar function on U.

(2)φ=φ(b2,s)satisfies(4.1)and

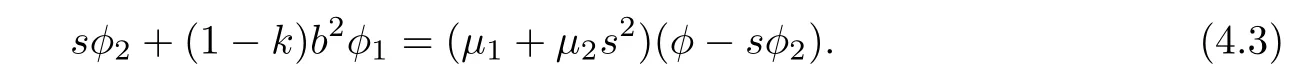
where k:=k(b2)/=1,μi:= μi(b2),i=1,2 and μ1+μ2b2= ?(k+1).Moreover,α and β satisfies

whereμ1+μ2b2=(k+1)and k=k(b2).In this case,dβ/=0.

(3)φ=φ(b2,s)satisfies(4.1)and

and β satisfies

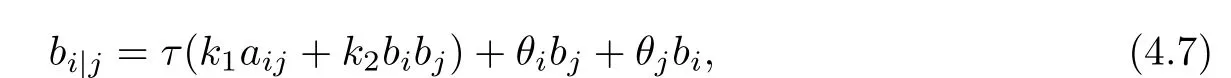
where θ := θiyiis a 1-form which is perpendicular to β. ξi:= ξi(b2),i=1,2 and ξ1+ξ2b2=

ProofAssume that case 1 holds.By(4.2),we have

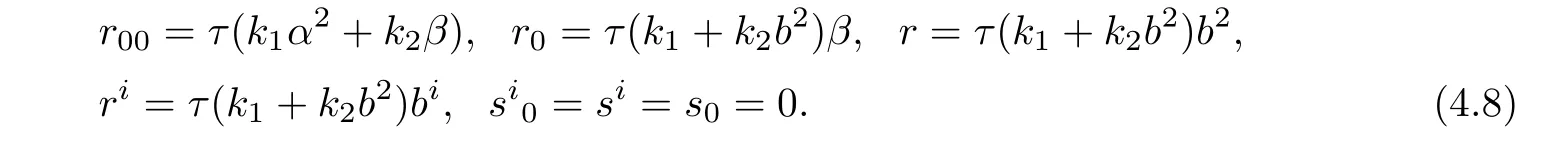
Plugging(4.8)into(2.5)yields

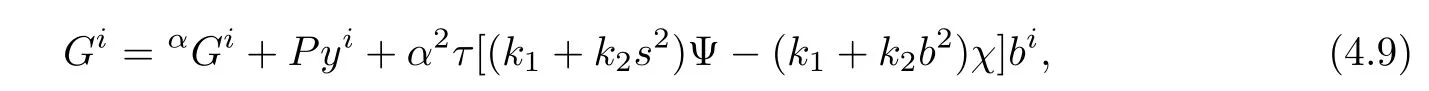
where χ :=R? 2RΨb2? sΠ and P:= ατ[(k1+k2s2)Θ+(2ΘRb2+s?)(k1+k2b2)].

Inserting(4.1)into(4.9)yields

Thus,it follows from(2.1)and(4.10)that F is a Douglas metric.

Assume that case 2 holds.By(4.4)and(4.5),we obtain

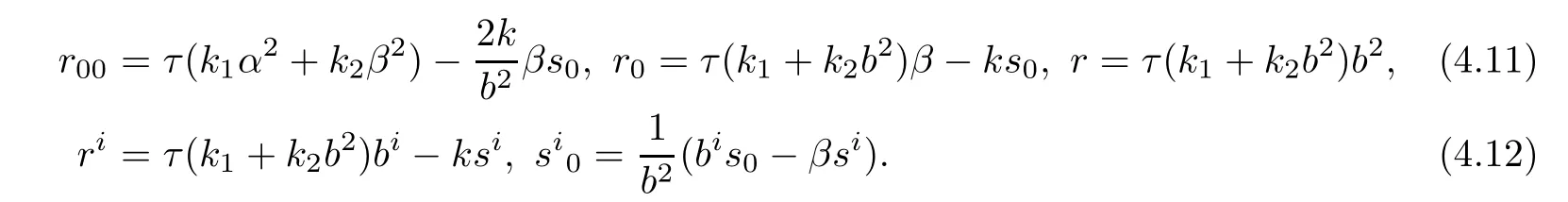
Inserting(4.1),(4.3),(4.11),(4.12)and(3.42)into(2.5)yields

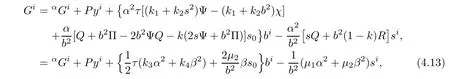
where we have used the first formula of(3.44)and P:= ατ[(k1+k2s2)Θ+(2ΘRb2+s?)(k1+Hence,from(2.1)and(4.13),then F is a Douglas metric.

Assume that case 3 holds.From(4.7),we obtain

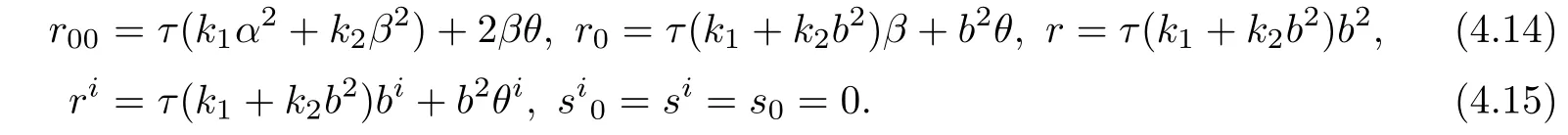
Plugging(4.14)and(4.15)into(2.5)yields

where P:= ατ[(k1+k2s2)Θ +(2ΘRb2+s?)(k1+k2b2)]+(2sΘ +b2?)θ.

Plugging(4.1),(4.6),and(3.57)into(4.16)yields

where we have used the first formula of(3.59).Hence,by(2.1)and(4.17),then F is a Douglas metric.

AcknowledgementsThe author would like to thank Professor Changtao Yu for his helpful discussion and the valuable comments.

[1]Bácsó S,Matsumoto M.On Finsler spaces of Douglas type.A generalization of the notion of Berwald space.Publ Math Debrecen,1997,51:385–406.MR 98j:53024

[2]Bryant R.Some remarks on Finsler manifolds with constant flag curvature.Houston J Math,2002,28:221–262

[3]Bácsó S,Matsumoto M.On Finsler spaces of Douglas type-a generalization of the notion of Berwald space.Publ Math Debrecen,1997,51:385–406

[4]Cheng X Y,Shen Z M.Projectively flat Finsler metrics with almost isotruplc-S-curvature.Acta Mathematica Scientia,2006,26B(2):307–313

[5]Li B L,Shen Y B,Shen Z M.On a class of Douglas metrics.Studia Sci Math Hung,2009,46:355–365

[7]Li B L,Shen Z M.On a class of projectively flat Finsler metrics with constant flag curvature.Int J Math,2007,18:749–760

[7]Li B L,Shen Z M.Projectively flat fourth root Finsler metrics.Can Math Bull,2012,55:138–145

[8]Matsumoto M.Finsler spaces with(α,β)-metric of Douglas type.Tensor(N S),1998,60:123–134

[9]Mo X H,Solórzano N M,Tenenblat K.On spherically symmetric Finsler metrics with vanishing Douglas curvature.DiffGeom Appl,2013,31:746–758

[10]Wang X M,Li B L.On Douglas general(α,β)-metrics,arXiv:1606.08043v1.

[11]Yu C T,Zhu H M.On a new class of Finsler metrics.DiffGeom Appl,2011,29:244–254

[12]Yu C T,Zhu H M.Projectively flat general(α,β)-metrics with constant flag curvature.J Math Anal Appl,2015,429:1222–239

[13]Zhou L F.Spherically symmetric Finsler metrics in Rn.Publ Math Debrecen,2012,80:67–77

[14]Zhu H M.On general(α,β)-metrics with vanishing Douglas curvature.Int J Math,2015,26(9):Article ID:1550076,16pp

[15]Zhu H M.A class of Finsler metrics of scalar flag curvature.DiffGeom Appl,2015,40:321–331