飛行器射前瞄準誤差概率分析與控制
張志勇 劉立輝 王 濤 段婧婧 田冠鎖 周 軍 潘建業 王 魁 王占濤
(1.中國運載火箭技術研究院,北京 100076; 2.北京航天計量測試技術研究所,北京 100076)
1 引 言
飛行器在發射前通過外部定向瞄準系統或自主對準、傳遞對準獲得自身慣性導航裝置測量坐標系的初始方位角,這一過程常被廣義簡稱為瞄準。瞄準精度不僅在飛行器純慣性導航飛行狀態下直接影響落點精度,即使在組合導航狀態下也與飛行器修正能力、末制導尋的能力等直接相關。
鑒于瞄準結果對飛行器正確飛行的重要性,在研制階段,需要進行充分的地面試驗以驗證飛行器系統具備的瞄準精度;在執行發射任務時,對于飛行器臨射前獲得的瞄準數據,無論源自外部方位基準還是自對準,通常也均采取進一步措施來保證其值在合格范圍內。
2 瞄準誤差的概率分布
飛行器的瞄準誤差是隨機的。自然世界中隨機變量的分布規律多種多樣,正態(常態)分布(normal distribution)(又名高斯分布(Gaussian distribution))是其中表現最為廣泛的一種形式,是自然科學研究的一個便捷模型。許多物理現象都被發現近似服從正態分布,盡管這些現象的根本原因經常是未知的,理論上可以證明如果把許多微小作用疊加起來看作一個變量,那么這個變量服從正態分布(R.N.Bracewell在《Fourier transform and its application》中進行了簡單證明);正態分布是一些離散分布和連續分布的極限分布[1]。
對于飛行器射前瞄準結果,既可以源自簡單的光學直接瞄準,也可以由復雜的地面設備與飛行器上設備的測量數據綜合解算得到。為此選取兩種系統的實裝試驗數據分析瞄準誤差與正態分布的相合性。
2.1 簡單形式的光學直接瞄準誤差
這一瞄準形式為有依托陣地地面光學瞄準儀器對準飛行器導航裝置瞄準棱鏡,涉及輸入量不到10個;標準值由基于相同原理的高精度儀器獲得。
試驗使用多臺不同裝備,由不同人員,在不同地點、不同季節和時段開展,累計進行93次瞄準操作,解算獲得瞄準誤差結果數據如下:
exS= [-12.2, 13.4, 28.6, 21.3, 21.1, 11.5, -0.1, -26.2, -17.7, -12.6, -5.3, -10.4, -39.0, -14.1, -14.0, 31.4, 12.3, 19.4, 17.2, 1.3, -13.3, -3.7, 55.4, -23.5, -17.6, -8.7, 5.7, -5.3, 11.2, -10.8, -18.8, 13.2, 1.8, -5.8, 7.7, 1.9, 16.7, 54.5, 55.3, 34.8, 28.7, 11.1, -37.2, -35.4, 2.2, -3.3, -5.6, 3.8, -2.5, -12.0, 2.9, 18.5, -9.1, -5.0, -3.1, -2.0, 23.9, 19.6, 4.6, 21.9, -4.1, -13.0, 22.9, 17.6, -11.6, -7.5, 3.2, -39.9, 15.2, 37.0, 3.2, 0.0, 29.8, 7.3, 3.7, 11.7, -38.8, -23.3, -23.5, 7.0, -4.3, 8.1, -6.0, 10.6, 0.3, -7.3, 10.4, -3.6, 4.2, 5.7, -5.3, -8.4, -11.5]
采用兩種方法對該樣本對應的總體分布是否符合正態分布進行檢驗。
2.1.1χ2檢驗
設瞄準誤差總體對應隨機變量ξS,其概率分布為F(x)。前述exS則為其中一個樣本的觀測量,其樣本均值MexS=2.0,樣本方差VexS=370.0。
檢驗假設H0:ξS~ N(2.0, 370.0),即
取6個分點將總體ξS分為 (-∞,t1], (t1,t2], (t2,t3],…, (t9, +∞)共7個區間,記Pi(i= 1,2,…,7)為總體ξS取值落入第i個區間的概率。
對于N(2.0, 370.0),取
t1=-20,t2=-10,t3=0,t4=10,t5=20,t6=30
有
P1=0.126 4,P2=0.140 0,P3=0.192 2,P4=0.202 7,
P5=0.164 0,P6=0.101 9,P7=0.072 7
記mi為樣本觀測值exS落入第i個區間的頻數,有
m1=9,m2=14,m3=22,m4=18,m5=16,
m6=8,m7=6
建立統計量
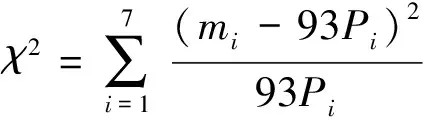
(2)
取顯著性水平α=0.05,拒絕域為
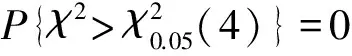
(3)
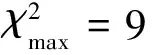
而由(2)式有
χ2|exS=2.061 4
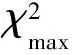
2.1.2 圖形檢驗
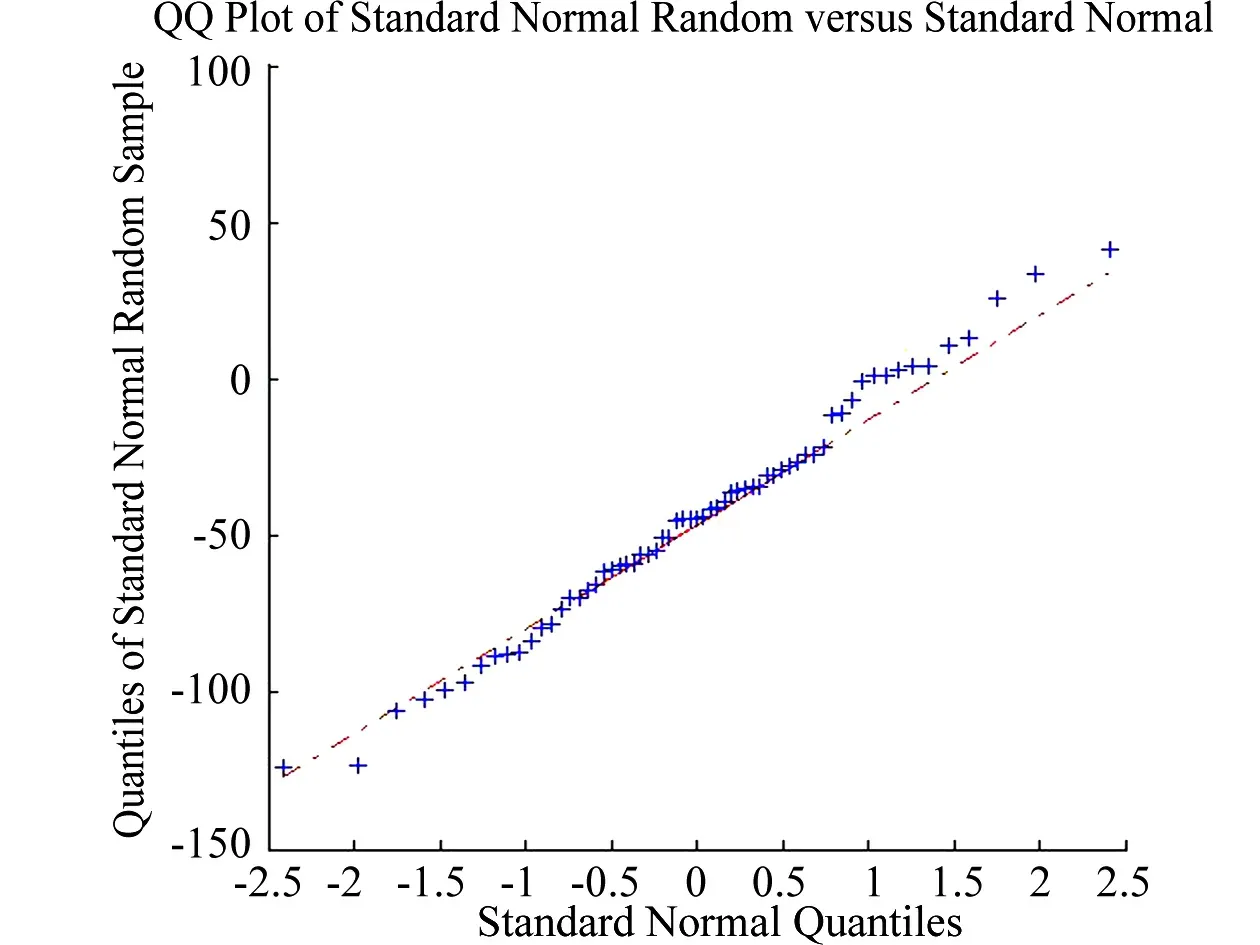
建立前述樣本觀測值exS的分位數圖(QQ圖),也可以直觀地看出簡單形式瞄準誤差是服從正態分布的。與按N(2.0, 370.0)生成隨機值建立的QQ圖比較,進一步驗證了這一結論。如圖1所示。
使用正態分布概率密度紙繪制簡單形式瞄準誤差樣本,同樣支撐前述結論。如圖2所示。
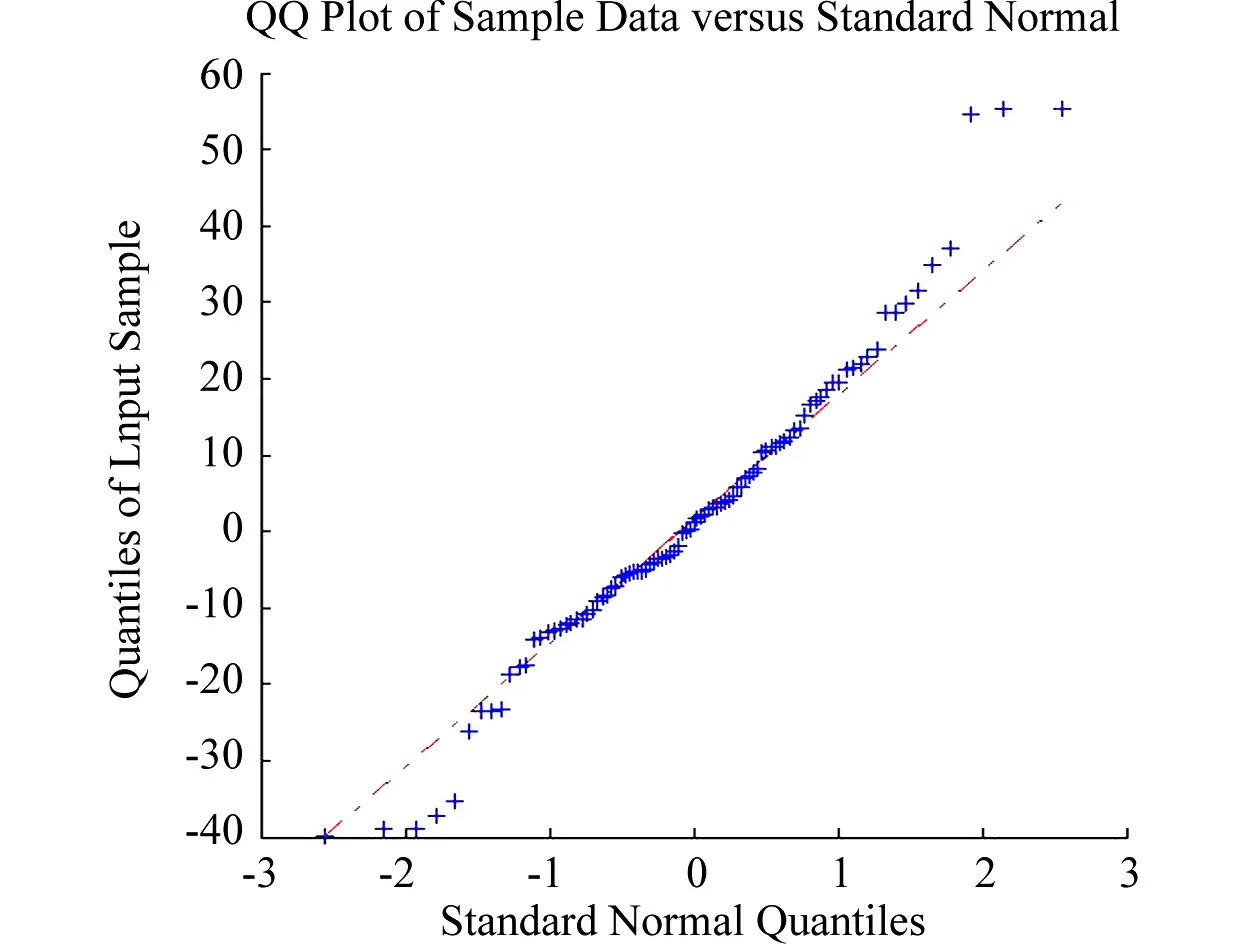
(a) 簡單形式瞄準誤差樣本(a) Simple pattern alignment error sample
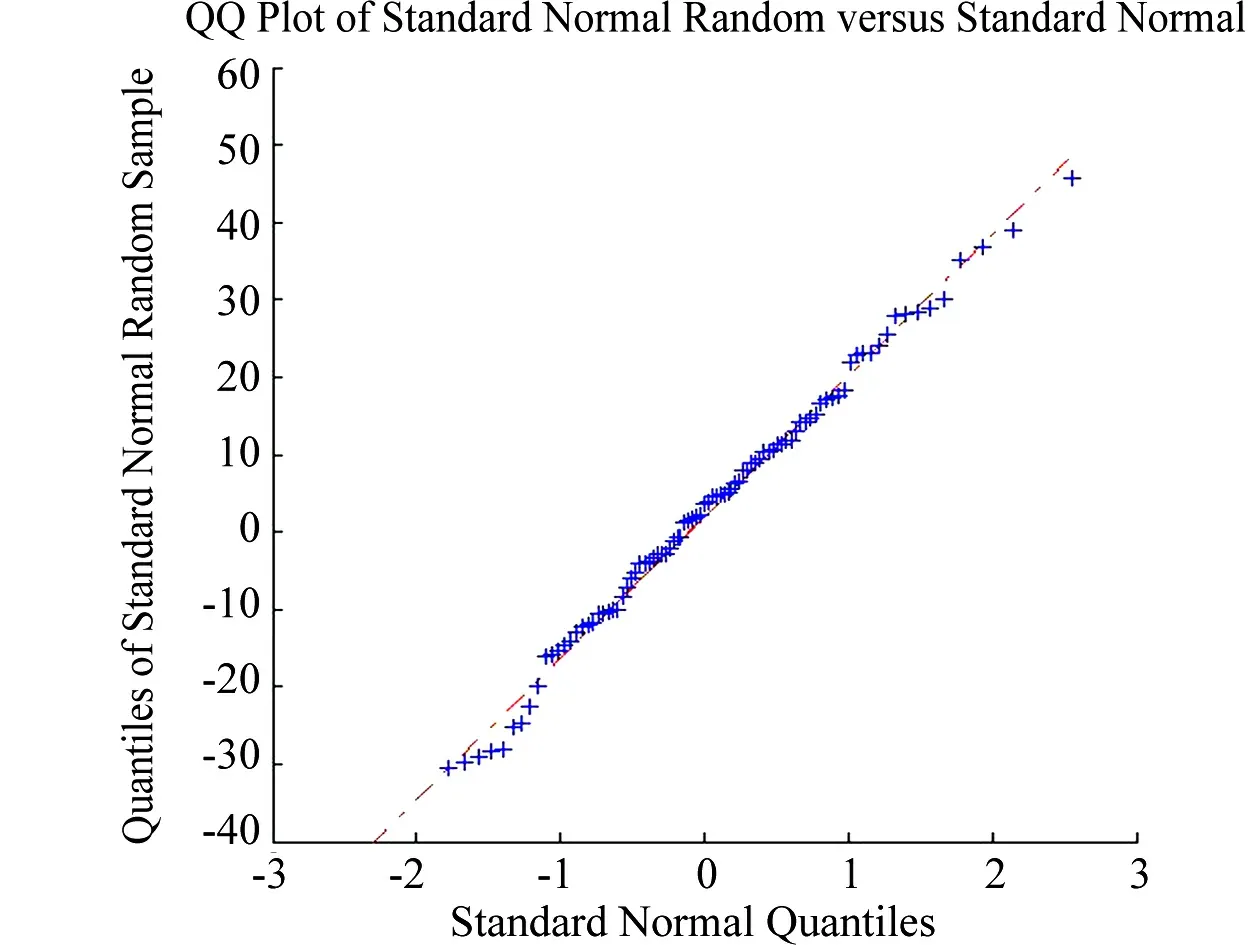
(b) 標準正態分布隨機樣本(b) Standard normal random sample
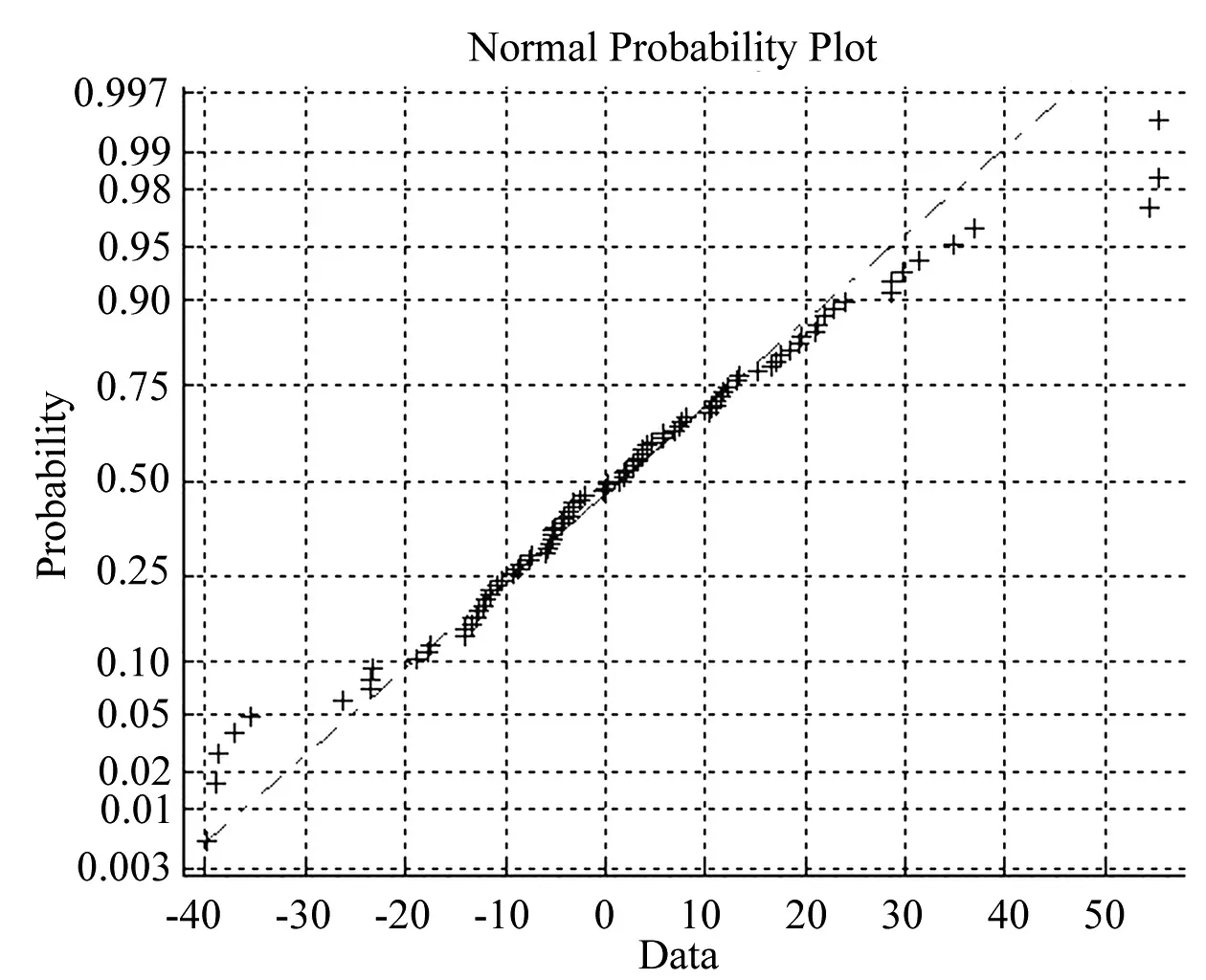
圖2 正態分布概率密度紙繪制簡單形式瞄準誤差樣本Fig.2 Simple pattern alignment error sample plotted on normal P.D. paper
2.2 復雜形式的慣性+光學間接瞄準誤差
這一瞄準形式使用飛行器和地面兩套慣性測量裝置的陀螺儀與加速度計預標和實時數據、自準直光管預標和實時數據、基準轉換裝置加速度計與棱鏡預標和實時數據等,涉及輸入量超過100個;標準值由基于有依托陣地地面光學直接瞄準原理的高精度儀器對準飛行器導航裝置瞄準棱鏡獲得。
試驗使用多臺不同裝備,在不同地點、不同時段開展,累計進行63次瞄準操作,解算獲得瞄準誤差結果數據如下:
exC=[ -52.4,7.3,52.6,-21.6,-32.5,-27.1, -38.1,-42.1,-30.2,-24.7,-51.3,-40.7,-45.2,-20.0,-33.5,-31.6,-42.1,-52.6,-29.7,-19.5,-43.8,-33.0,-40.6,-106.2,-100.4,-85.2,-30.8,-22.1,-0.8,-60.8,-58.4,-35.5,-54.8,-43.4,-35.0,-70.5,-16.1,-41.4,-38.4,-79.1,-53.1,-71.0,43.3,-46.3,-80.1,-83.2,20.0,-74.1,84.6,-74.1,-67.7,-61.2,-76.6,-83.3,-87.8,-64.9,-56.8,-79.3,-71.2,-9.9,-12.0,-9.0,-33.2]
2.2.1χ2檢驗
設瞄準誤差總體對應隨機變量ξC,其概率分布為F(x)。前述exC則為其中一個樣本的觀測量,其樣本均值MexC= -41.6,樣本方差VexC= 1 211.3。
按前述方法,取
t1=-80,t2=-64,t3=-48,t4=-32,t5=-16,t6=0
計算可得
χ2|exC=6.024 7
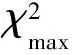
2.2.2 圖形檢驗
通過exC的QQ圖,同樣可直觀地看出復雜形式瞄準誤差也是服從正態分布的。與按N(-41.6, 1 211.3)生成隨機值建立的QQ圖比較,同樣進一步驗證了這一結論。如圖3所示。
圖4是使用正態分布概率密度紙繪制復雜形式瞄準誤差樣本的情況,亦支撐前述結論。
(b) 標準正態分布隨機樣本(b) Standard normal random sample
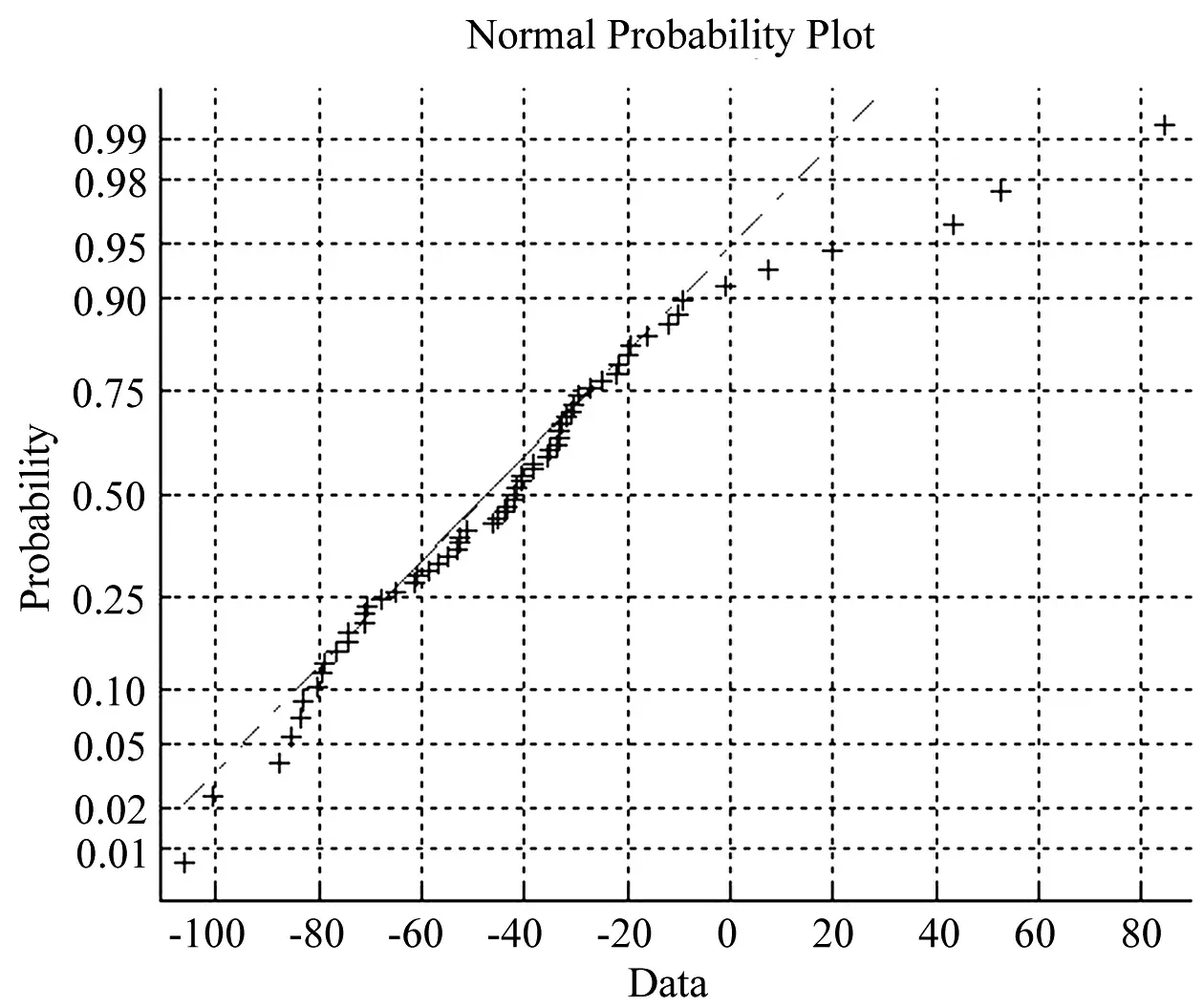
圖4 正態分布概率密度紙繪制復雜形式瞄準誤差樣本Fig.4 Complex pattern alignment error sample plotted on normal P.D. paper
3 試驗次數與精度可信度
瞄準誤差是隨機變量,通過有限次數的試驗、有限容量的樣本不能精確獲知包含未來的無限總體的數字特征。基于瞄準誤差服從正態分布,在總體期望(均值)與方差未知的情況下,可以按給定置信度對數字特征進行估計。
理論上,系統的誤差均值可以通過方案設計(例如在線自調零)或生產、檢測工藝等途徑加以抑制,而方差表征系統輸出結果的離散程度,在通過有限次試驗推斷將來系統正式工作時的精度表現方面尤為重要,故此對樣本方差的可信度展開分析。

則置信區間為
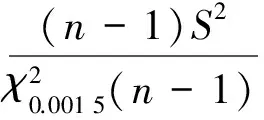
可見區間端點是試驗次數(樣本容量)n的函數。
設自由度為ν的χ2分布關于上分位點α的累加函數為F(α|ν),有

其中
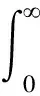
(5)
設置信區間左端點關于n的函數為lci(n)、右端點關于n的函數為rci(n),有
(6)式、(7)式函數曲線如圖5所示。
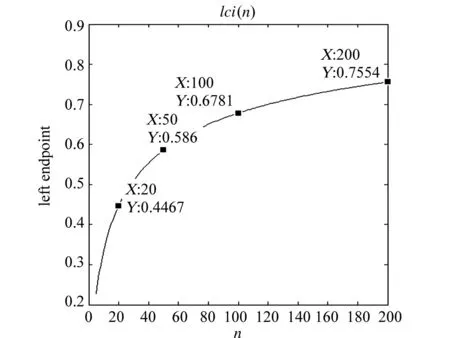
(a) 左端點函數(a) Left end-point function
圖5 方差置信區間端點函數曲線
Fig.5Curves of variance confidence interval end-point function
可以看出,左端點函數關于n單調增加,值小于1;右端點函數關于n單調減小,值大于1。即試驗次數越多,置信區間越窄,獲得的樣本方差表征總體方差越精確。
表1列出了若干試驗次數對應的總體方差0.997置信區間寬度系數,圖6為兩者關系的圖形化表示,可以看出,在試驗次數少于100時,置信區間寬度受試驗次數影響很大,其后增加試驗次數,效果并不非常顯著。
表1方差0.997置信區間寬度與試驗次數的關系
Tab.1Relationbetweenvariance0.997confidenceintervalwidthandexperimentfrequency
類似地,可以建立服從t分布的隨機變量,對總體期望進行估計。圖7為總體期望0.997置信區間寬度與試驗次數的關系曲線,可見前述關于方差的結論同樣適用。
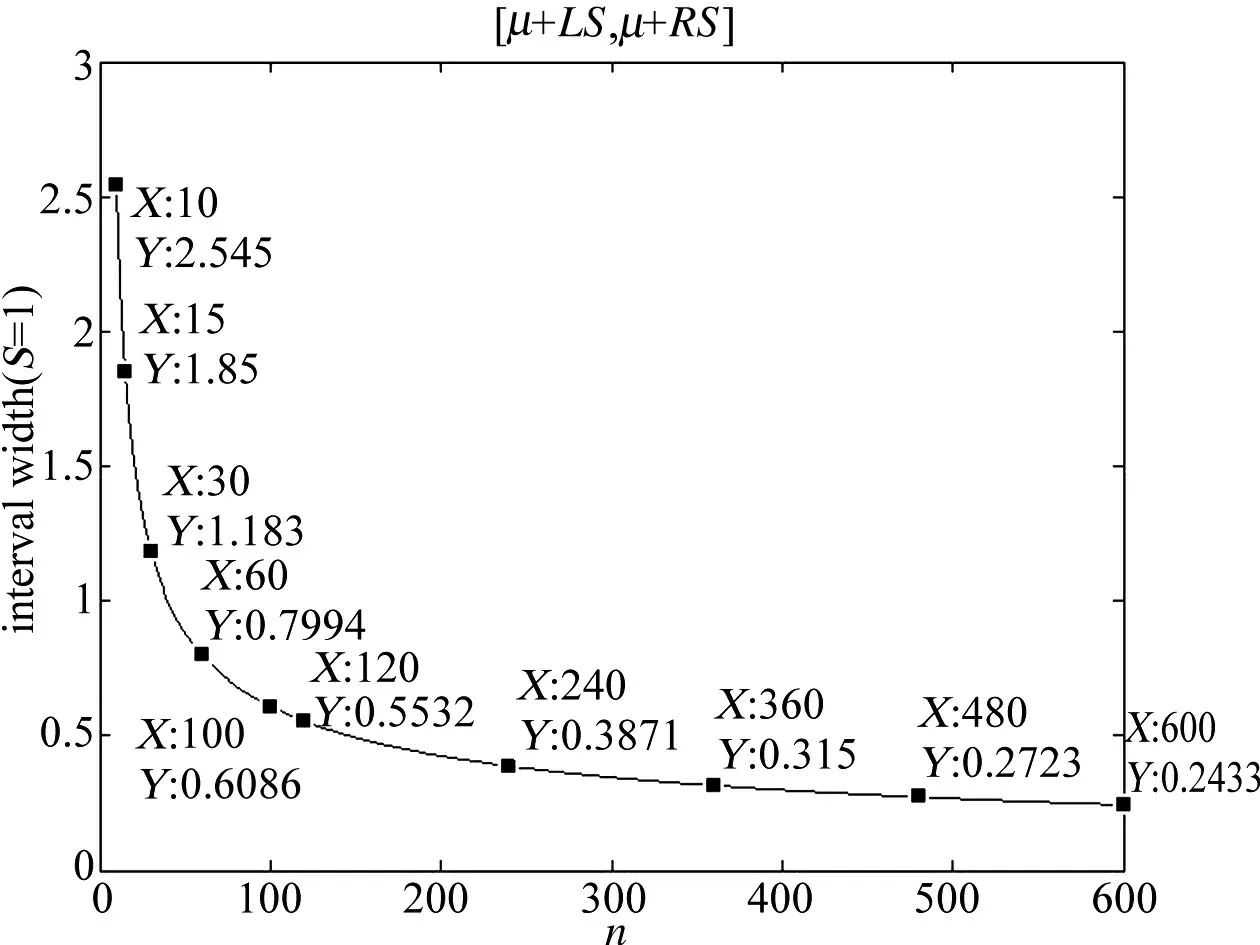
圖7 期望0.997置信區間寬度與試驗次數的關系Fig.7 Relation between expectation 0.997 confidence interval width and experiment frequency
4 射前瞄準精度保障措施
根據前述分析,對飛行器瞄準精度的確定需要大容量樣本支撐,這在工程上可能難以實現。對此,在執行飛行試驗任務時,可采取配置瞄準校準系統的措施來進一步控制飛行器瞄準精度。
設飛行器射前方位對準(瞄準)允差為εT,飛行器瞄準系統(A)誤差指標為εA(εA<εT)、當次瞄準結果為zA,瞄準校準系統(C)誤差指標為εC(εC≤εA)、當次瞄準結果為zC,|zA-zC|的判別閾值為th。(注:關于誤差的指標均取正值。)
對于判別閾值的設置,可以采取極值處理方法,本文也提出基于概率的處理方法。
4.1 基于極值的閾值
對于同一個指標,控制漏判和錯判不能兼顧。為確保發射后飛行任務成功,判據(判別閾值)選擇以保證飛行器射前不出現漏判為原則。
設定飛行器方位對準結果zA與校準系統結果zC的差值的合格判據為不大于th=εT-εC,則在zC誤差達到極值且zA、zC誤差同向的最差情況下,也能夠保證不出現漏判,為飛行器導航提供可接受的方位初值;另一方面,在一定程度上,例如zA誤差不大于th-εC(不小于0)、zC誤差達到極值且zA、zC誤差反向時,也能夠保證不會錯判。
4.2 基于概率的閾值
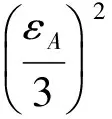
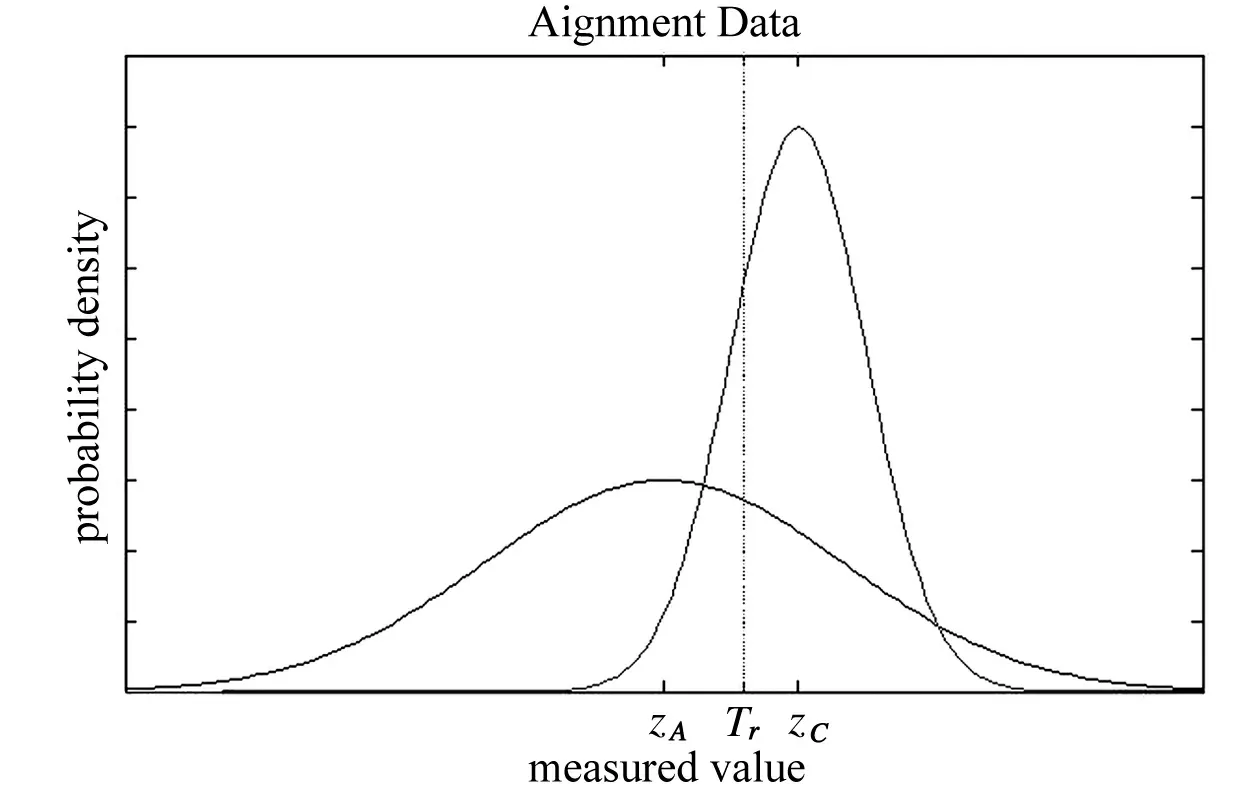
圖8 描述同一物理量的兩個隨機變量Fig.8 Random variables describing the same physical quantity
為保證瞄準系統的輸出結果可用,應有
Tr∈[zA-εT,zA+εT]
(8)
現以更高精度的ζC描述(8)式的概率,有
P{ζC≤zA+εT|zC}-P{ζC≤zA-εT|zC}=0.997
(9)
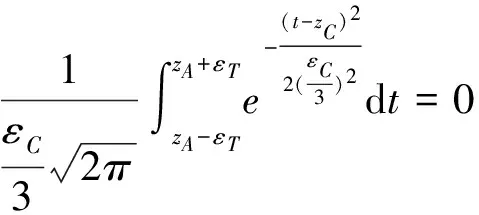
(9)式概率值與兩個隨機變量均值的間距(|zA-zC|)相關而與變量均值的位置無關,可簡述為th=f(εT,εC)。在εT和εC確定后,可利用MATLAB工具計算出th值。
可進一步驗證,基于概率確定的合格判據(th值)相比基于極值確定的判據略為寬松,在真實世界更具合理性,在依概率保證精度的同時,也提升了飛行器發射流程的順利性。
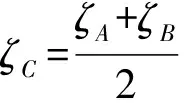
5 結束語
通過以上分析,表明無論簡單或是復雜的飛行器瞄準系統,所得瞄準結果服從正態分布;為更準確地通過樣本表征正態總體,瞄準系統精度試驗應充分開展(宜不少于100次);通過配置瞄準校準系統,基于正態分布概率確定對瞄準結果的判別閾值,能夠更有效地保證飛行器發射任務的圓滿完成。
[1] rns521. 正態分布[EB/OL]. (2011-11-09) [2017-10-20]. http://blog.csdn.net/rns521/article/details/6953591.
[2] MathWorks. MATLAB Product HelpDoc[CP/DK]. U.S.: The MathWorks, Inc, 2015.

