地統計學與支持向量機相融合的建筑工程造價預測①

劉 春

(四川建筑職業技術學院 網絡管理中心,德陽 618000)

1 引言

隨著我國經濟水平的不斷提高,人們住房、生活得到了大幅度的改善,出現了許多大型建筑. 在建筑構建過程中,工程造價是大家關心的重要問題,其直接影響到工程的管理、成本以及其它方面,因此建立高精度的建筑工程造價預測模型一直是人們關注的焦點[1-3].

建筑工程造價建模常基于時間序列數據進行,把建筑工程造價看作是一種按時間前后順序組織在一起的數據,數據之間存在明顯時序特性,同時受到其它因素影響,具有較強的非線性變化特點. 傳統建筑工程造價預測模型有：多元性線回歸,滑動平均模型等,它們屬于線性建模方法,無法描述建筑工程造價的非線性變化特征,建筑工程造價預測結果不太可靠[4,5]. 近些年,人們將神經網絡引入到了建筑工程造價的建模中,由于具有非線性預測能力,獲得了比傳統模型更高的建筑工程預測精度[6-8]. 神經網絡要求建筑工程造價的歷史數據多,如果歷史數據太少,會出現“過擬合”的建筑工程造價預測結果. 支持向量機(Support Vector Machine,SVM)是一種非線性建模能力強的算法,克服了神經網絡對訓練樣本規模的約束條件,預測性能要優于神經網絡,為建筑工程造價提供了一種新的建模工具[9]. 如何對歷史數據間的時間相關性進行有效挖掘十分關鍵,常采用拓階的方法實現,拓階過程消耗時間長,而且屬于線性拓階方法,結果無法描述建筑工程造價的非線性變化特性. 為了精確對建筑工程造價進行預測,根據對建筑工程造價樣本時間相關性和非線性變化特點,構建了基于地統計學與支持向量機相融合的建筑工程造價預測模型,并通過建筑工程造價預測實例對性能進行測試與分析.

2 支持向量機與地統計學

基于支持向量機的建筑工程造價預測建模過程中,由于根據建筑工程造價數據間的時間相關性,由支持向量機自身無法確定表示時間相關性的嵌入維數,地統計學(Geostatistics,GS)[10,11]是一種時序特性分析法,可以將變程作為時間序列的階數,即嵌入維數,而且工作過程簡單、執行速度快,可以用于確定支持向量機的建筑工程造價時間序列拓階.

2.1 支持向量機

式中,w為權向量,b為閾值,為高維特征空間的映射函數.

為了使預測結果的風險最小化,建立如下的經驗風險函數：

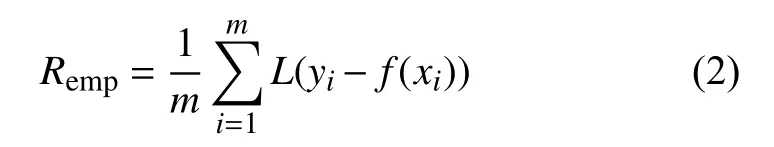
式中,L為損失函數,具體為

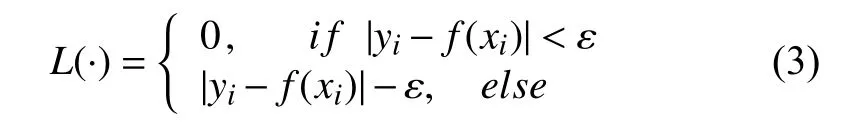
式中,ε是回歸誤差的閾值[12].

對于小樣本預測問題,基于經驗風險原理進行建模可能導致預測結果差,為此支持向量機考慮了泛化風險,得到如下回歸函數：

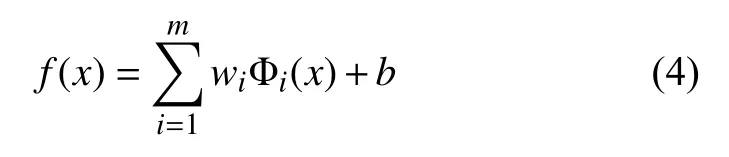
式(4)可以轉化為求解以下函數規劃問題：

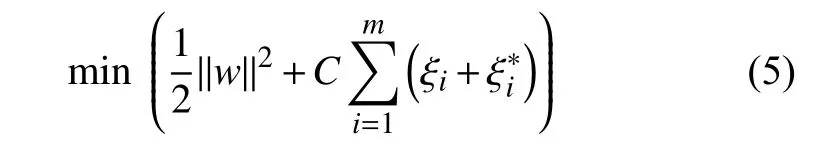
約束條件為：

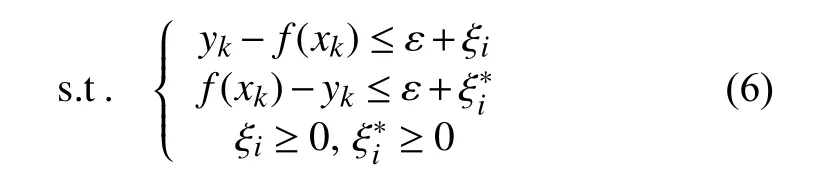
引入拉格朗日算子 得到式(6)的對偶問題,然后進行求解可得：

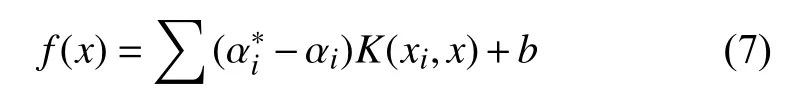
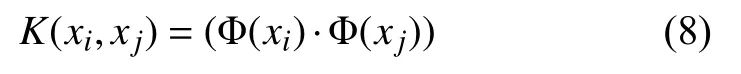
本文采用RBF函數,其定義為

在建筑工程造價進行建模時,相關研究表明,下一時刻建筑工程造價與前m個建筑工程造價相關,即時間序列的嵌入維數,用yk+1表示當建筑工程造價,那么建筑工程造價的預測原理可以表示為：

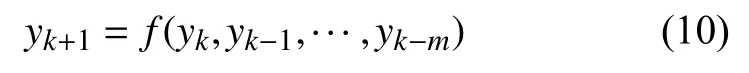
2.2 地統計學

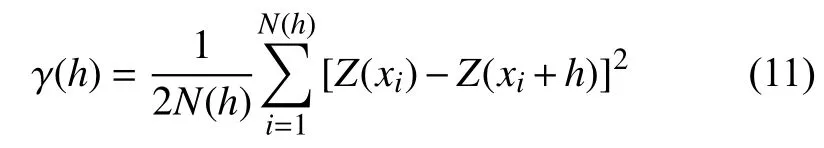
協方差函數定義為：

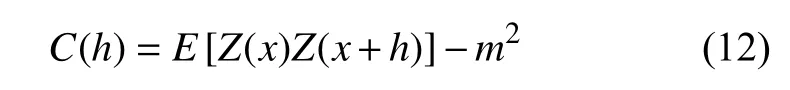
式中,h表示時間間隔距離.

3 GS-SVM的建筑工程造價預測模型

(1) 收集建筑工程造價相關數據,得到數據形式為X={x1,x2,…,xn},并進行如下處理.

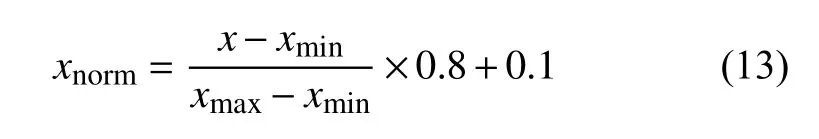
(2) 采用地統計學通過變程確定建筑工程造價的最優嵌入維數,具體為：根據不同h,由式(11)得到不同的γ(h),剛開始,h與γ(h)之間是一種線性變化關系,當h超過一定距離后,γ(h)得到第一個最大值,該γ(h)的值為基臺值,此時的h為變程,用α表示,即得到了時間序列的嵌入維值.

(3) 根據最優嵌入維數和建筑工程造價的影響因素構建支持向量機的輸入向量,與相應的建筑工程造價組成學習樣本.

(4) 將建筑工程造價訓練樣本集輸入支持向量機,并設置支持向量機參數,建立建筑工程造價預測模型.GS-SVM的工程造價建模過程如圖1所示.

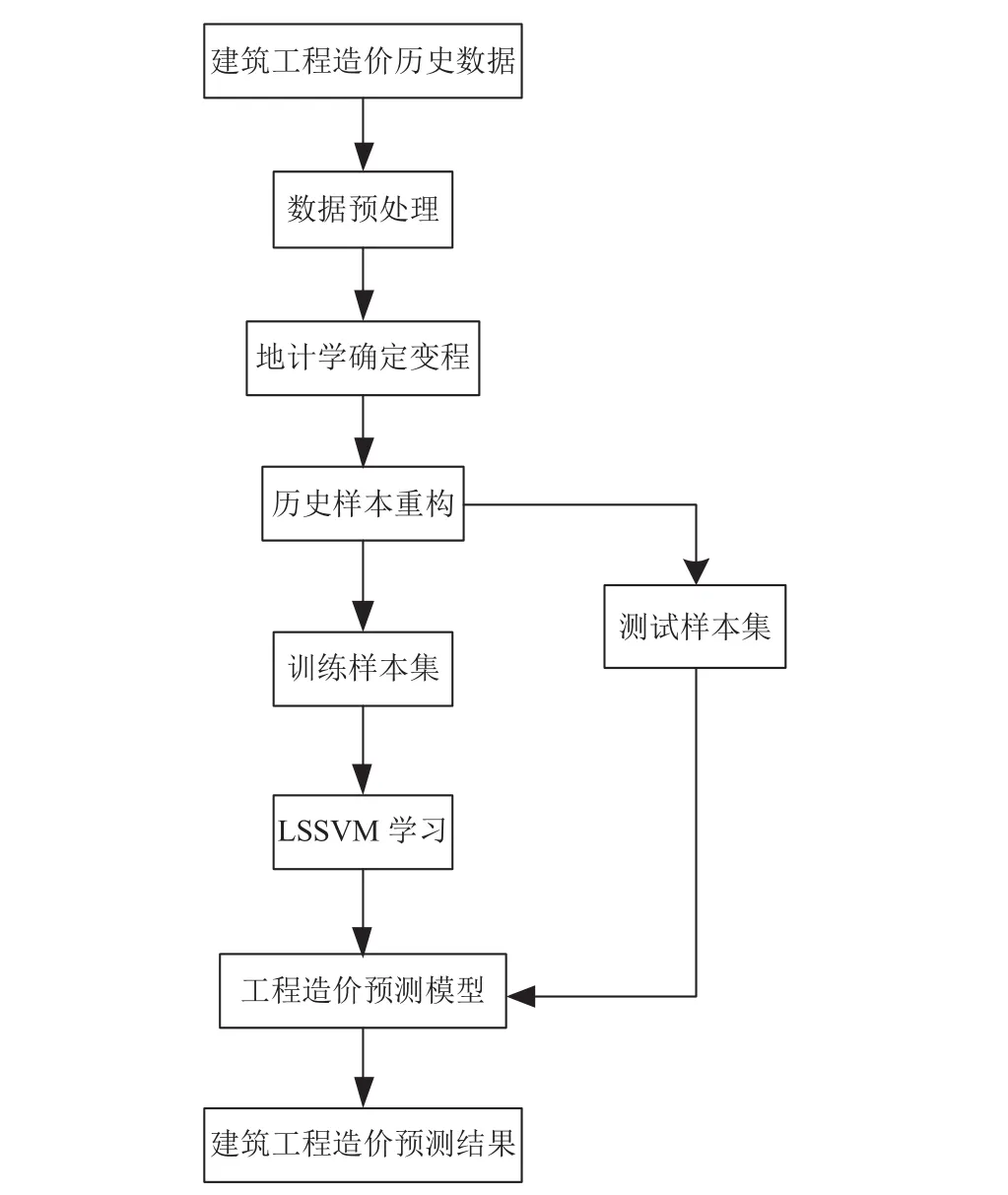
圖1 工程造價預測模型的工作流程

4 建筑工程造價預測實例

4.1 數據來源

選擇某市2000～2016年的每月工程造價數據作為研究對象,共獲得180個樣本,采用單層面積、層數、層高、承載力、基深作為影響,工程造價數據如圖2所示,以130個月數據作為訓練樣本,建立建筑工程造價預測模型,其余50個樣本對建筑工程造價預測模型的泛化能力進行測試.

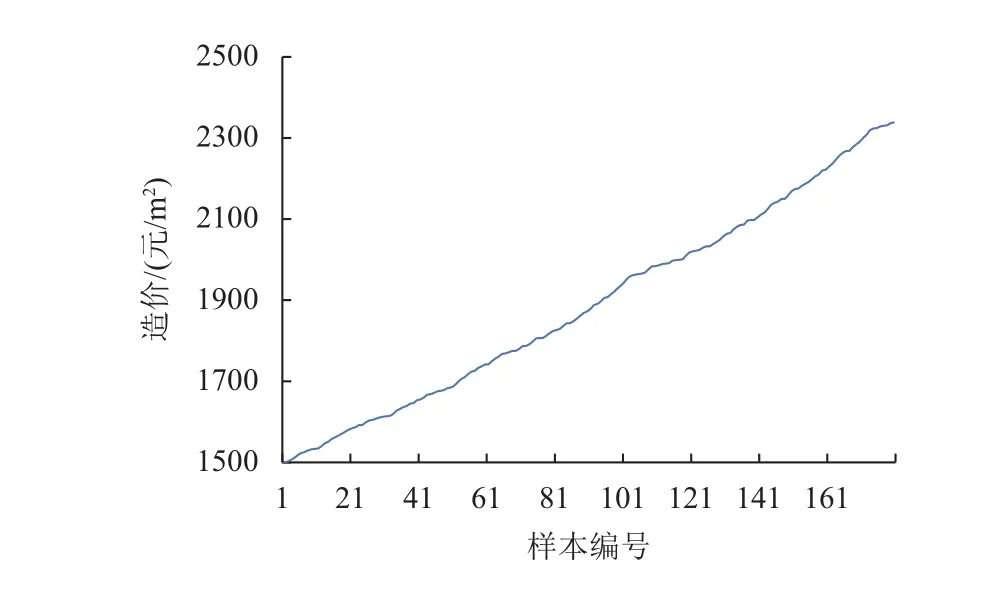
圖2 實驗對象

從圖2可知,2000～2016年的每月建筑工程造價數據具有明顯上升變化態勢,為此建立建筑工程造價模型之前,對原始數據進行去趨勢平穩化法處理,具體如下：

首先對2000～2016年的每月建筑工程造價數據取對數,然后進行擬合,即

根據式(14)得到去趨勢平穩化后的2000～2016年的每月建筑工程造價數據：

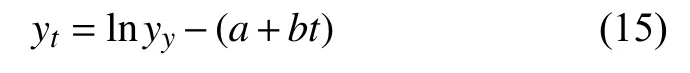
后續建模基于平穩化后的建筑工程造價數據.

4.2 基于GS確定建筑工程造價數據嵌入維數

建筑工程造價不僅與單層面積、層數、層高、承載力、基深等因素有關,而且與前一段時間的建筑工程造價相關,因此,建筑工程造價時間序列具有明顯的時間關聯特性,對平穩化后的建筑工程造價數據進行地統計學分析,得到建筑工程造價的半變異函數如圖3所示. 從圖3可知,變程α=5,即建筑工程造價與前5個月的建筑工程造價相關,因此嵌入維數為5. 前5個月的建筑工程造價數據與單層面積、層數、層高、承載力、基深作為輸入,構建支持向量機的學習樣本.

4.3 結果與分析

4.3.1 GS-SVM的預測結果

通過十折交叉驗證法確定支持向量機的參數：C=240.80,σ=1.784,GS-SVM的建筑工程造價預測結果如圖4所示. 從圖4可知,GS-SVM的建筑工程造價預測精度相當高,能夠較好描述建筑工程造價的變化特點,GS-SVM可以應用于實際的建筑工程造價中.

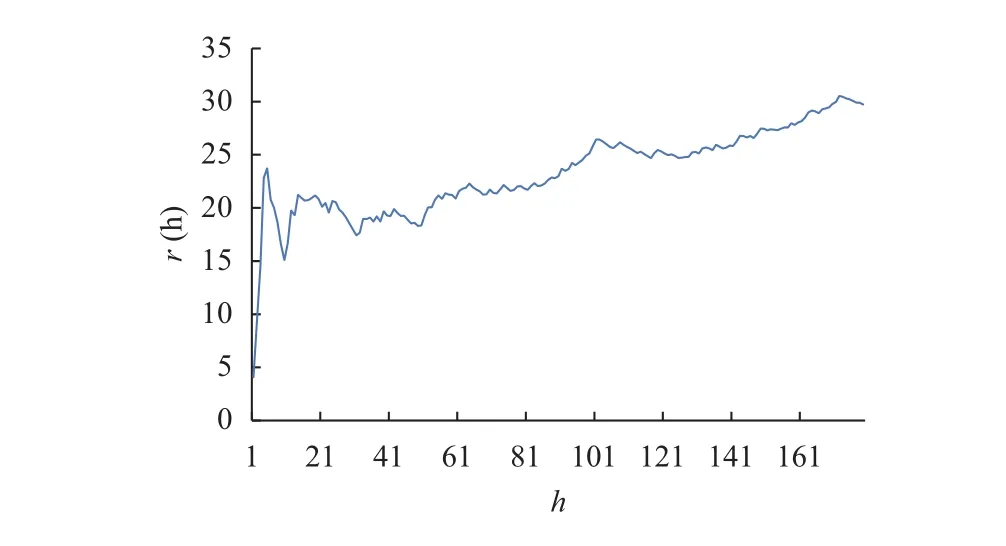
圖3 建筑工程造價的半變異函數圖

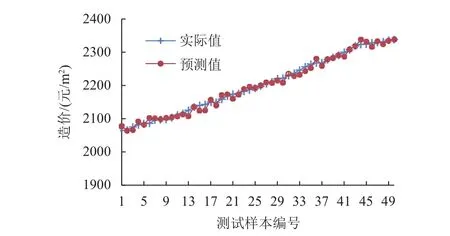
圖4 GS-SVM的建筑工程造價預測結果

4.3.2 與其它模型的預測結果

比較采用多元線性回歸模型(MLR)、支持向量機(SVM)、地統計學與BP神經網絡(GS-BPNN)作為對比模型,采用平均預測精度作為建筑工程造價預測結果好壞評價指標. 統計所有模型的建筑工程造價預測精度,得到結果如表1所示. 對表1的實驗結果進行分析,可知：

(1) 單一支持向量機(SVM)沒有考慮建筑工程造價數據的時序動態特性,沒有進行拓階操作,只是簡單采用影響因素作為輸入變量,導致建筑工程造價預測精度低.

(2) 多元線性回歸模型(MLR)的建筑工程造價最低,說明其不能準確描述建筑工程造價的變化特點,獲得了較高的建筑工程造價預測誤差,沒有什么實際應用價值.

(3) GS-BPNN的建筑工程造價平均預測精度得到了一定提升,這主要由于通過GS對建筑工程造價時間序列進行拓階處理,描述了數據的時序動態特性,大幅度降低了建筑工程造價的預測誤差,表明引入變程可以有效提高建筑工程造價預測精度.

(4) GS-SVM的建筑工程造價預測精度最高,這是因為采用支持向量機對建筑工程造價進行建模,克服了神經網絡大樣本要求,泛化能力優異,并通過GS描述建筑工程造價數據的時序特性,建立理想的建筑工程造價預測模型,相比對比模型,建筑工程造價預測精度具有明顯優勢.

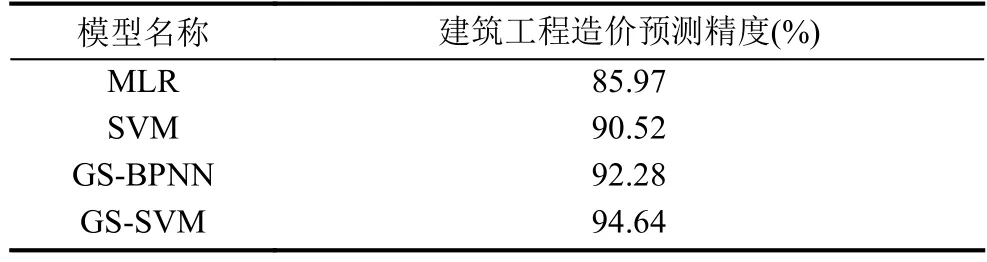
表1 建筑工程造價的預測精度對比

5 結束語

針對建筑工程造價中的訓練樣本選擇問題,以及非線性變化特點,綜合利用地統計學和支持向量機的優點,設計了基于GS-SVM的建筑工程造價預測模型,通過地統計學快速確定時間序列的嵌入維數,然后通過支持向量機建立建筑工程造價的非線性預測模型,具體應用實例測試結果表明,GS-SVM大幅度提高了建筑工程造價的預測精度,具有廣泛的應用前景.

1 陳鵬,劉亞南. 建筑工程造價管理的現狀與對策. 工業工程,2015,34(48)：33-34.

2 張利榮. 多基元模糊算法在工程估價中的應用. 施工技術,2010,39(6)：64-66.

3 胡六星. 基于時間序列的建筑工程造價預測研究. 太原理工業大學學報,2012,43(6)：706-709,714.

4 郭一斌,王紅革,王翔. 基于Vague集貼近度的工程項目投資快速估算方法. 現代經濟信息,2011,12(2)：50-55.

5 孟俊娜,梁巖,房寧. 基于BP神經網絡的民用建筑工程造價估算方法研究. 建筑經濟,2015,36(9)：64-68.

6 胡曉娟. 多元線性回歸模型參數的STLS估計法及其在工程造價預測中的應用. 四川建筑科學研究,2016,42(4)：142-147.

7 牛東曉,乞建勛,邢棉. 建筑工程造價預測的變結構神經網絡模型研究. 華北電力大學學報,2001,28(4)：1-4.

8 李杰. 改進粒子群算法優化支持向量機的工程造價預測.計算機系統應用,2016,25(6)：202-206.

9 Li GQ,Deng M,Zhu JJ,et al. Spatial outliers detection considering distances among their neighbors. Journal of Remote Sensing,2009,13(2)：197-202.

10 Petitgas P,Woillez M,Doray M,et al. A geostatistical definition of hotspots for fish spatial distributions.Mathematical Geosciences,2016,48(1)：65-77. [doi：10.1007/s11004-015-9592-z]

11 劉莘,張紹良,王飛,等. 基于地統計學的空間離群點檢測算法的研究. 計算機應用研究,2016,33(12)：3700-3704.[doi：10.3969/j.issn.1001-3695.2016.12.040]

12 王雪松. 改進支持向量機的網絡流量預測. 計算機系統應用,2017,26(3)：230-233.