考慮多因素的兩類沉降預(yù)測(cè)方法比選

王志華

道路建設(shè)最基本的要求就是滿足強(qiáng)度和穩(wěn)定性。而表征道路整體穩(wěn)定性的重要指標(biāo)之一就是沉降量。沉降量的預(yù)測(cè)為施工時(shí)間、施工方案、后期營運(yùn)養(yǎng)護(hù)提供相應(yīng)的參數(shù)或者技術(shù)指標(biāo)。沉降量的測(cè)定方法可以通過實(shí)驗(yàn)室測(cè)定，現(xiàn)場測(cè)定和相關(guān)經(jīng)驗(yàn)來評(píng)估[1]。

目前，對(duì)于路基沉降預(yù)測(cè)的方法可分為兩大類：①根據(jù)固結(jié)理論，結(jié)合土的本構(gòu)模型計(jì)算最終沉降量，主要包括經(jīng)典的分層總和法和各種數(shù)值分析方法，主要有限元法、差分法、無網(wǎng)格法和邊界元法等[2]。這類方法的固結(jié)參數(shù)可能因樣品干擾、樣品大小和應(yīng)變等因素而導(dǎo)致預(yù)測(cè)不準(zhǔn)確。②數(shù)學(xué)擬合。目前，已有的路基沉降預(yù)測(cè)研究方法包括：沉降曲線擬合法（雙曲線法、指數(shù)曲線法、泊松曲線法、三點(diǎn)法、S型曲線法等）；Asaoka方法；人工神經(jīng)網(wǎng)絡(luò)法；遺傳算法；灰色預(yù)測(cè)法；有限元法等[3]。這類方法由于擬合中沒有考慮土的本構(gòu)模型，因此預(yù)測(cè)的準(zhǔn)確主要依賴于實(shí)測(cè)沉降數(shù)據(jù)，而且路基沉降測(cè)量往往針對(duì)典型工點(diǎn)和局部地段進(jìn)行量測(cè)，數(shù)據(jù)少、效率低且費(fèi)用高[3～4]。因此，基于上述兩種沉降預(yù)測(cè)方法在應(yīng)用中存在的問題，本研究根據(jù)湘桂某道路沉降資料，利用PSO-ANN對(duì)路基沉降進(jìn)行預(yù)測(cè)，試圖為處理道路沉降提供技術(shù)依據(jù)。

1 PSO-ANN模型沉降預(yù)測(cè)

1.1 PSO-ANN方法簡介

人工神經(jīng)網(wǎng)絡(luò)（ANN）是通過權(quán)重和偏差相互連接的神經(jīng)元網(wǎng)絡(luò)。一個(gè)典型的人工神經(jīng)網(wǎng)絡(luò)模型如圖1所示。一旦人工神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)形成，下一個(gè)任務(wù)就是訓(xùn)練網(wǎng)絡(luò)。

網(wǎng)絡(luò)訓(xùn)練意味著找到網(wǎng)絡(luò)中各種權(quán)重和偏差的最優(yōu)值。通常，使用各種類型的技術(shù)來找到ANN的權(quán)重和偏差的合適值[5]。在本研究中，通過粒子群優(yōu)化（PSO）獲得了網(wǎng)絡(luò)的最優(yōu)訓(xùn)練。

圖1 BP網(wǎng)絡(luò)結(jié)構(gòu)

PSO從這種模型中得到啟示并用于解決優(yōu)化問題。PSO中，每個(gè)優(yōu)化問題的潛在解都是搜索空間中的一只鳥，稱之為粒子。所有的粒子都有一個(gè)由被優(yōu)化的函數(shù)決定的適值（fitness value），每個(gè)粒子還有一個(gè)速度決定它們飛翔的方向和距離。然后粒子們就追隨當(dāng)前的最優(yōu)粒子在解空間中搜索[5～7]。

PSO初始化為一群隨機(jī)粒子（隨機(jī)解），然后通過迭代找到最優(yōu)解[8]。在每一次迭代中，粒子通過跟蹤兩個(gè)極值來更新自己；第一個(gè)就是粒子本身所找到的最優(yōu)解，這個(gè)解稱為個(gè)體極值；另一個(gè)極值是整個(gè)種群目前找到的最優(yōu)解，這個(gè)極值是全局極值。另外也可以不用整個(gè)種群而只是用其中一部分作為粒子的鄰居，那么在所有鄰居中的極值就是局部極值[8～9]。

假設(shè)在一個(gè)D維的目標(biāo)搜索空間中，有N個(gè)粒子組成一個(gè)群落，其中第i個(gè)粒子表示為一個(gè)D維的向量：

第i個(gè)粒子的“飛行”速度也是一個(gè)D維的向量，記為：

第i個(gè)粒子迄今為止搜索到的最優(yōu)位置稱為個(gè)體極值，記為：

整個(gè)粒子群迄今為止搜索到的最優(yōu)位置為全局極值，記為：

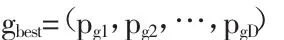
在找到這兩個(gè)最優(yōu)值時(shí)，粒子根據(jù)如下的公式（2.1）和（2.2）來更新自己的速度和位置：

其中：c1和 c2為學(xué)習(xí)因子，也稱加速常數(shù)（acceleration constant），r1和r2為[0，1]范圍內(nèi)的均勻隨機(jī)數(shù)[8]。由三部分組成，第一部分為“慣性（inertia）”或“動(dòng)量（momentum）”部分，反映了粒子的運(yùn)動(dòng)“習(xí)慣（habit）”，代表粒子有維持自己先前速度的趨勢(shì)；第二部分為“認(rèn)知（cognition）”部分，反映了粒子對(duì)自身歷史經(jīng)驗(yàn)的記憶（memory）或回憶（remembrance），代表粒子有向自身歷史最佳位置逼近的趨勢(shì)；第三部分為“社會(huì)（social）”部分，反映了粒子間協(xié)同合作與知識(shí)共享的群體歷史經(jīng)驗(yàn)，代表粒子有向群體或鄰域歷史最佳位置逼近的趨勢(shì)，根據(jù)經(jīng)驗(yàn)，通常：c1=c2=2。i=1，2，…，D。vid是粒子的速度，vid=∈[-vmax，vmax]，vmax是常數(shù)，由用戶設(shè)定用來限制粒子的速度。r1和r2是介于[0，1]之間的隨機(jī)數(shù)[8]。

在借鑒傳統(tǒng)BP神經(jīng)網(wǎng)絡(luò)的基礎(chǔ)上，使用PSO對(duì)BP神經(jīng)網(wǎng)絡(luò)進(jìn)行優(yōu)化，依據(jù)以下7個(gè)步驟進(jìn)行了訓(xùn)練：

步驟1：收集數(shù)據(jù)；

步驟2：創(chuàng)建網(wǎng)絡(luò)；

步驟3：配置網(wǎng)絡(luò)；

步驟4：初始化權(quán)重和偏差；

步驟5：使用PSO訓(xùn)練網(wǎng)絡(luò)；

步驟6：驗(yàn)證網(wǎng)絡(luò)：

步驟7：使用網(wǎng)絡(luò)。

1.2 沉降值預(yù)測(cè)實(shí)例

本論文采用觀測(cè)樁和沉降板兩種方法對(duì)的某道路進(jìn)行沉降觀測(cè)，選取了2個(gè)測(cè)點(diǎn)的743個(gè)數(shù)據(jù)進(jìn)行預(yù)測(cè)研究，由于數(shù)據(jù)較大，見表1。為了根據(jù)充填階段預(yù)測(cè)沉降曲線，采用PSO-ANN法，首先選擇分析參考階段[10]。例如，如果在一個(gè)站點(diǎn)中使用了三個(gè)路堤構(gòu)造階段，那么參考階段有三選擇。然后，需要反映在場地特性中的土壤參數(shù)。這些數(shù)據(jù)可以從實(shí)驗(yàn)室和原位測(cè)試中獲得。最后，需要一個(gè)粒子群安裝狀態(tài)。使用所有選定的數(shù)據(jù)、C1和C2計(jì)算，而Cc、Ch和F是通過PSO-ANN方法對(duì)被監(jiān)視的沉降數(shù)據(jù)進(jìn)行反分析所估計(jì)的值[3]。圖2顯示了PSO-ANN預(yù)測(cè)結(jié)果和真值和相關(guān)系數(shù)（左）及最小適應(yīng)性曲線（右）。從該圖可以看出，回歸系數(shù)R為0.99353。

圖2 PSO-ANN預(yù)測(cè)結(jié)果和真值和相關(guān)系數(shù)（左）及最小適應(yīng)性曲線（右）

現(xiàn)在，使用訓(xùn)練好的神經(jīng)網(wǎng)絡(luò)可以用于知道未知輸入特征的輸出。讓所述數(shù)據(jù)集的訓(xùn)練好的ANN的輸入特征為test_input，其輸出結(jié)果如下所示。

Calculation of MSE of total test data 0.438538.

實(shí)際上，test_input是從附表I取得的一組數(shù)據(jù)集，訓(xùn)練網(wǎng)絡(luò)的輸出（test_output） 結(jié)果顯示：Calculation of MSE of total real data err_real=0.51151。若將該組數(shù)據(jù)中填筑階段作為一組數(shù)據(jù)集，訓(xùn)練網(wǎng)絡(luò)的輸出（test_output） 結(jié)果顯示：Calculation of MSE of total real nocomplete data err_realno=0.5548。若將該組數(shù)據(jù)中填筑完成階段作為一組數(shù)據(jù)集，訓(xùn)練網(wǎng)絡(luò)的輸出（test_output）結(jié)果顯示：Calculation of MSE of total complete real data err_realyes=0.2208。從結(jié)果可以看出，PSO-ANN模型對(duì)后期沉降預(yù)測(cè)較準(zhǔn)確。

2 線性回歸模型沉降量預(yù)測(cè)

表1 沉降量實(shí)驗(yàn)方差分析結(jié)果

表2 沉降量實(shí)驗(yàn)線性回歸分析結(jié)果

表1顯示沉降量實(shí)驗(yàn)方差分析結(jié)果，測(cè)定時(shí)間（Day）、測(cè)點(diǎn)（No）、距中線位置（Local）、填筑階段（Stage）、填筑高度（Height）四個(gè)因素對(duì)沉降量實(shí)驗(yàn)有顯著性影響。將這四種因素和沉降量做回歸分析，線性回歸模型的均方誤差（MSE）為0.9023855，隨機(jī)選137個(gè)樣本，線性回歸模型的真值和預(yù)測(cè)值的MSE為1.237389。對(duì)照上面PSO-ANN模型，線性回歸模型的均方誤差約高1倍，由此可見PSO-ANN模型的預(yù)測(cè)準(zhǔn)確性遠(yuǎn)遠(yuǎn)由于線性回歸模型。

3 結(jié)束語

本文針對(duì)道路沉降預(yù)測(cè)問題展開研究，利用已監(jiān)測(cè)的數(shù)據(jù)，采用PSO-ANN神經(jīng)網(wǎng)絡(luò)進(jìn)行了研究，通過對(duì)比分析得出：PSO-ANN神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)模型收斂速度更快和精度更高，驗(yàn)證了PSO-ANN神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)道路沉降的有效性和可行性。該方法可通過Matlab計(jì)算，操作簡單，通用性較強(qiáng)，能進(jìn)一步提高沉降預(yù)測(cè)精度和收斂速度。本研究在兩個(gè)斷面、六個(gè)位點(diǎn)進(jìn)行了現(xiàn)場沉降觀測(cè)，通過現(xiàn)有預(yù)測(cè)方法、PSO-ANN的預(yù)測(cè)值和實(shí)際沉降量的對(duì)比，說明這種方法在沉降預(yù)測(cè)中的準(zhǔn)確性。

[1]賀勇，諸克軍，胡承凡.品位組合優(yōu)化的粒子群-神經(jīng)計(jì)算方法.系統(tǒng)管理學(xué)報(bào)，2010（02）：204～209.

[2]梁小叢，付金丹.基于PSO和ANN復(fù)合的邊坡穩(wěn)定性評(píng)價(jià)模型.山西建筑，2009（29）：114～115.

[3]張道法，陳濤.基于GA-PSO-ANN算法的隧洞巖土參數(shù)反分析.人民珠江，2015（06）：71～73.

[4]Chenglei H.，L.Kangji，L.Guohai，et al.Forecasting Building Energy Consumption Based on Hybrid PSO-ANN Prediction Model.in第三十四屆中國控制會(huì)議.2015.中國浙江杭州.

[5]Feng X.，S.Li，C.Yuan，et al.，Prediction of Slope Stability using Naive Bayes Classifier.KSCE Journal of Civil Engineering，2018，22（3）：941～950.

[6]Koopialipoor M.，A.Fallah，D.J.Armaghani，et al.，Three hybrid intelligent models in estimating flyrock distance resulting from blasting.Engineering with Computers，2018：1～14.

[7]Lee S，I.ParkJ.-K.Choi，Spatial prediction of ground subsidence susceptibility using an artificial neural network.Environmental management，2012，49（2）：347～358.

[8]Tian H.，J.ShuL.Han，The effect of ICA and PSO on ANN results in approximating elasticity modulus of rock material.Engineering with Computers，2018：1～10.

[9]Li C.，A simplified method for prediction of embankment settlement in clays.Journal of Rock Mechanics and Geotechnical Engineering，2014，6（1）：61～66.

[10]張航，丁文霞.軟土路基沉降觀測(cè)點(diǎn)的布設(shè).公路交通技術(shù)，2003（02）：13～14.