基于航跡質量分析的加權平均融合算法
李素
(四川大學計算機學院,成都,610065)
0 引言
融合估計系統的典型結構分集中式、分布式與混合式三種[1]。其中,分布式融合結構能夠以較低的費用得到較好的可靠性和可用性。如圖1所示,在分布式多傳感器航跡融合系統中[2],各傳感器周期性地將傳感器量測發送至跟蹤器,跟蹤器進行目標跟蹤處理得到局部航跡(傳感器航跡),然后,將跟蹤輸出的局部航跡傳送至融合中心進行融合處理。航跡融合包括航跡關聯和航跡狀態估計融合兩步。其中,在航跡關聯過程中,系統將來自各傳感器的局部航跡進行兩兩關聯;而在航跡狀態估計過程中,融合中心通過相應的航跡融合算法將那些經過航跡關聯后判定為來自同一目標的局部航跡進行融合,形成系統航跡。
一直以來,航跡融合算法都是分布式多傳感器融合系統中的一個關鍵技術[3]。現有的航跡融合算法有加權平均融合方法、簡單融合方法、動態權值融合方法等。
加權平均融合是一種有效處理多源傳感器數據問題的經典方法,傳統的加權平均融合將每一路測量信息完全平均的加權,但并沒有考慮傳感器因自身差異而導致測量誤差相差較大的問題。本文算法將系統航跡與局部航跡的歐氏距離以及其狀態向量在1范數下的距離之和作為航跡質量測量度,并進行航跡質量分析,同時剔除航跡質量較差的局部航跡,再根據航跡質量確定各局部航跡的加權因子,最后用加權平均方法進行航跡狀態估計,避免了航跡融合效果受傳感器自身測量誤差的影響,同時也解決了當傳感器數量增加到一定數目時融合精度并沒有持續提高甚至下降的問題。
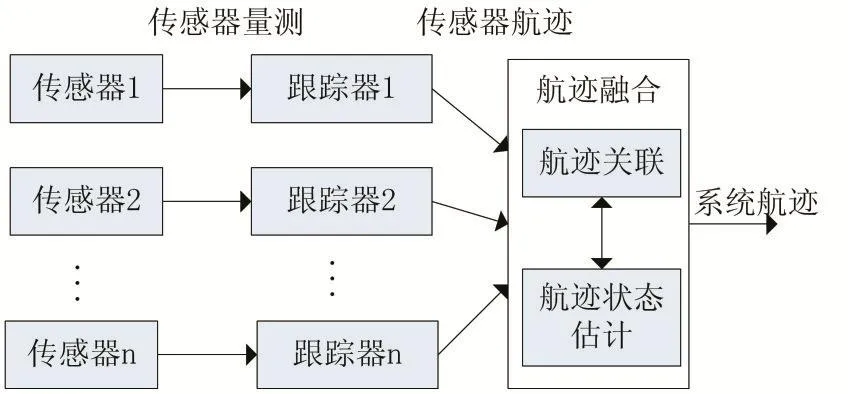
圖1 分布式多傳感器融合系統結構框圖
1 航跡融合
一般情況下,當傳感器的測量誤差越小,其局部航跡的航跡質量越好,當傳感器的測量越大時,其局部航跡的航跡質量越差。統計方差分析法將局部航跡在各個時刻的平均方差作為評價航跡質量的方法[4],這種方法平均了各局部航跡誤差,并不能完全體現出各局部航跡在航跡質量上的差異,從而難以獲得最優的加權因子。本文將系統航跡與局部航跡的歐氏距離以及其狀態向量在1范數下的距離之和作為評價航跡質量的標準,能有效度量各局部航跡的航跡質量。而根據航跡質量來確定加權因子,則航跡質量高的局部航跡對應的加權因子大,航跡質量低的局部航跡對應的加權因子小,能保證加權因子分配的合理性和有效性。
另外,將每一路的局部航跡信息都進行融合處理的做法雖然能整合多路傳感器的信息,但并沒有考慮到傳感器因自身差異而導致測量誤差相差較大的問題。信息量越多并不能保證融合結果的精度越高[5]。因此,在進行航機狀態估計融合時,本文提出設置航跡質量門限值,剔除航跡質量較差的局部航跡,將航跡質量較好的局部航跡進行融合,能有效減少異常值對融合結果的影響,從而避免傳感器測量誤差對系統航跡精度的影響。
算法描述:
Step1計算航跡質量
假設系統航跡集合為Ts,來自各個傳感器的局部航跡集合為Tp:

其中,系統航跡集合中系統航跡數目為ns,記為:

局部航跡集合中局部航跡數目為np,記為:

假設與系統航跡xsi關聯的局部航跡共m條,其中,局部航跡i表示為:

對應的系統航跡 j表示為:

局部航跡i和系統航跡 j歐氏距離定義為:
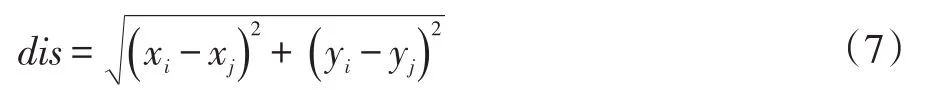
局部航跡i和系統航跡 j狀態向量為:
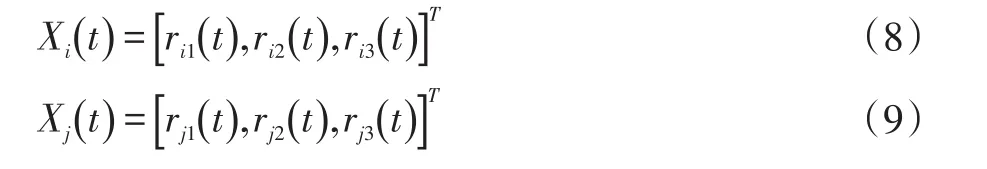
式中,rk為航跡特征。
局部航跡i和系統航跡 j狀態向量在1范數定義下的距離為:

航跡i和航跡 j的距離測度定義為:

局部航跡i在t時刻的航跡質量定義為:

Step2剔除航跡質量較差的局部航跡
設置航跡質量門限:
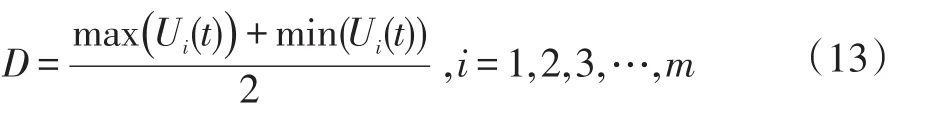
根據局部航跡的航跡質量和設置的門限值,刪除航跡質量小于門限值的局部航跡,保留航跡質量大于等于門限值的局部航跡。
根據航跡質量分配權值,對應的權值為:

Step3加權融合
對保留的局部航跡進行航跡狀態估計融合,最終得到系統航跡。加權融合航跡為:
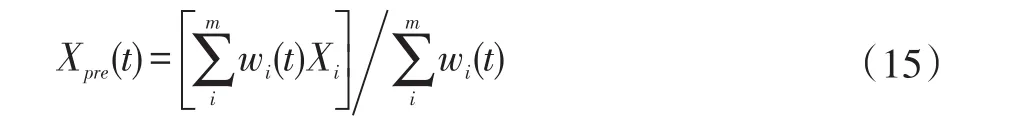
Xi是局部航跡i的狀態向量,Xpre(t)為融合得到的系統航跡。
算法流程圖如圖2所示。
2 仿真實驗
2.1 實驗環境
實驗模擬目標在二維空間做勻速直線運動,使用3部傳感器同時觀測1個目標,傳感器掃描周期均為4s,且目標均在傳感器觀測范圍之內。3部傳感器周期性地輸出局部航跡報告,融臺程序將接收到的航跡數據先進行航跡關聯處理,然后對關聯成功的航跡進行航跡融合處理,最后輸出融合結果。
為了驗證本文算法的有效性,模擬3個具有不同測量誤差的傳感器,3個傳感器的坐標位置以及分辨率誤差如下:
S1:(-25000,10000),δ=40
S2:(53066.6425,50000),δ=100
S3:(10000,-83406.3881),δ=200
并進行100次Monte Carlo航跡融合處理仿真實驗,每次實驗仿真測試30個周期,并計算各傳感器量測值、量測融合方法輸出的系統航跡及本文算法輸出的系統航跡的平均誤差。
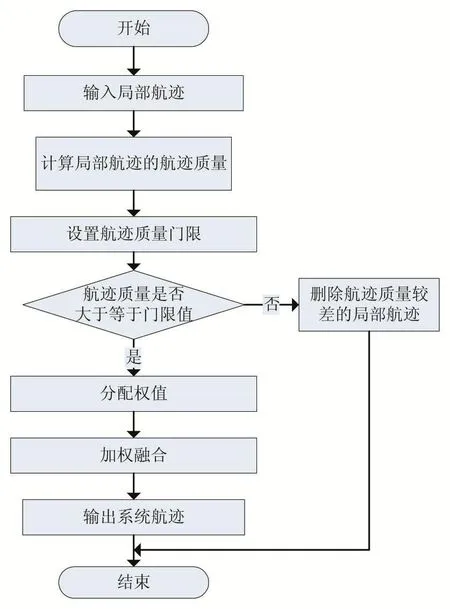
圖2 融合算法流程圖
2.2 仿真實驗結果
表1給出了各傳感器量測值、量測融合方法輸出的系統航跡及本文算法輸出的系統航跡的平均誤差。通過量測融合以后,有效地綜合了3個傳感器的測量值,提高了分辨率相對低、測量誤差相對大的傳感器的測量效果,但是其終融合精度仍然無法高于分辨率最高、測量誤差最小的傳感器的測量效果。而本文算法的融合航跡誤差明顯降低,且低于測量誤差最小的傳感器的測量值。
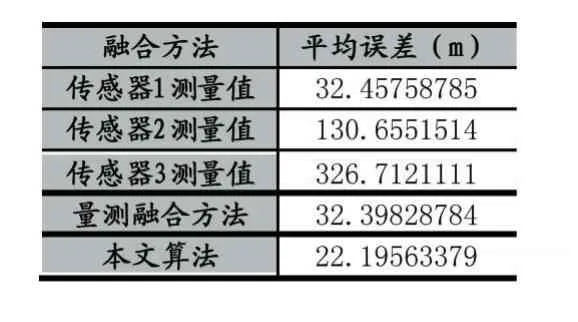
表1 平均誤差
圖3、圖4分別給出了測量值與量測融合方法融合誤差比較及測量值與本文算法融合誤差比較,實驗結果顯示本文算法的融合精度明顯高于測量融合方法的精度,且對目標狀態的預估更穩定。
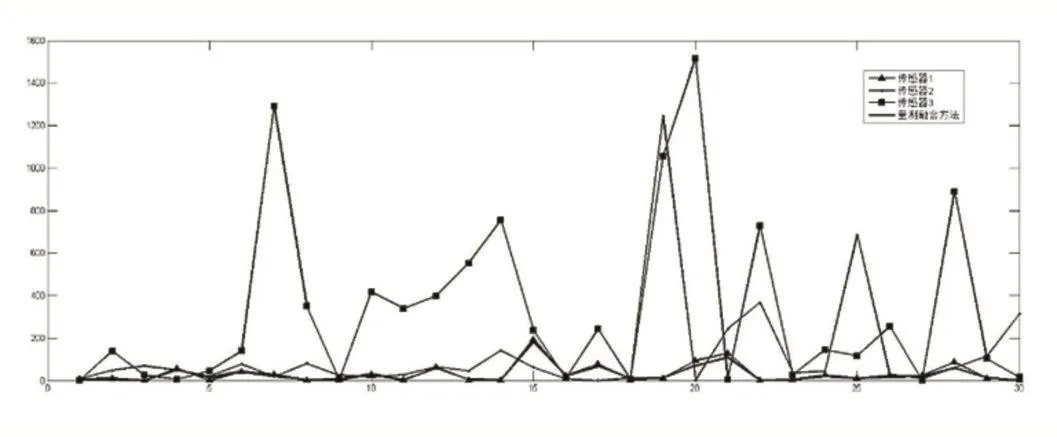
圖3 測量值與量測融合方法融合誤差比較

圖4 測量值與本文算法融合誤差比較
2.3 仿真結果分析
在分布式多傳感器航跡融合系統中,多個傳感器可以有效提高系統的探測能力和,但是隨著傳感器數量增加會影響數據傳輸效率,因此,考慮覆蓋區域面積和避免覆蓋冗余,在仿真實驗中使用3部傳感器。在仿真實驗中分別模擬三種不同實驗場景,并進行100次Monte Carlo實驗,驗證算法在目標密集的環境下是否有效。
以上實驗結果表明,本文算法有效地綜合了各個傳感器的測量值,且融合輸出的系統航跡精度高于單個傳感器的觀測值,達到了航跡融合的目的,驗證了本文算法的有效性。
3 結語
量測融合方法只是將估計誤差最小的局部估計作為全局估計,這種方法實際上沒有對傳感器航跡進行真正的融合。而本文算法基于局部航跡的航跡質量分配各局部航跡的權值,并刪除了航跡質量較差的局部航跡,因而能在融合中心提取精確度更高的數據,致使融合精度大大提高。
該算法不僅計算簡單便與實現,而且克服了航跡融合效果受傳感器自身測量誤差的影響等局限性。在三個不同的實驗場景中,本文分別給出了3個傳感器的量測值、量測融合方法輸出的系統航跡及本文算法輸出的系統航跡的平均誤差,并進行了對比,實驗結果驗證了本文算法的有效性。
參考文獻:
[1]韓紅,劉允才,韓崇昭等.多傳感器融合多目標跟蹤中的序貫航跡關聯算法[J].信號處理,2004,20(1):30.
[2]韓崇昭等.隨機系統概論[M].清華大學出版社,2014:269.
[3]劉健波,王運鋒.分布式雷達航跡融合關鍵技術研究[J].四川大學學報工程科學版,2006,38(6):119.
[4]徐麗.目標密集環境下的多傳感器航跡融合算法研究[D].哈爾濱工業大學,2012.
[5]張偉,王澤陽,張可.基于多模型航跡質量的融合算法[J].計算機科學,2013(2):65-70.

