基于動態反向映射圖的流圖劃分方法
李茜錦
(四川大學計算機學院,成都 610065)
0 引言
圖經常被用來對應用問題進行抽象建模,把圖劃分為更小的塊是一個基本的算法操作,對于遍歷、路徑尋找等問題,圖劃分通常是一個減少復雜性或并行化的重要子問題。隨著應用中更大的圖的實例的出現,例如科學估算、社會網絡或者合作交易網絡,圖劃分變得越來越重要和困難,同時通過在圖上執行計算來提取知識變得越來越具有挑戰性。
為了找到越來越亟需的快速圖劃分方法,將流這一概念與圖劃分相結合的流圖劃分算法被提出[8]。流圖劃分追求卓越的劃分速度,隨之而來還有許多等待解決的問題,包括異構環境、有向圖與無向圖等,雖然已經出現了異構環境中的流圖劃分[11]等對流圖算法的改進,但對有向圖和無向圖進行區分的研究仍然欠缺。
在流圖劃分中,每次只能處理一個元數據,而元數據只包含非常有限的信息:當前頂點和其鄰居,或者當前頂點和其某一個鄰居。對于無向圖來說,這種有限的數據總能獲得當前頂點的完整信息,但是對于有向圖,在元數據中無法獲得當前頂點的所有信息,甚至由于流的限制,在以頂點為中心的劃分方法中,劃分結果會忽略所有的沒有出度的頂點。同時,有向圖是無法回避的一個問題,社交網絡、交流通訊網絡等都存在大量的有向圖,所以本文提出了動態反向映射圖來解決有向流圖劃分的問題。
1 相關工作
圖劃分有長久的研究歷史,蘊含很多問題以及或簡或繁的解決方法。一般來說,所討論的圖劃分都為平衡圖劃分,平衡圖劃分是一個NP完全問題[1-2],其有兩個需要達到的目標,第一是盡可能減少被分區切割的邊的數量,第二是每個分區有大致相同的大小。顯然,如果去掉平衡這一限制,第一個目標會非常容易達到最優。平衡圖劃分給定一個圖G和數字k,把G劃分為k個大小相差不多的子圖,同時最小化被切割的邊的數量。
全局算法根據整個圖的信息來計算劃分結果,對于大圖而言非常不適用,所以啟發式方法被提出以解決圖劃分問題。Kernighan和Lin[3]第一個提出啟發式方法——KL算法,而后Fiduccia和Mattheyses[4]提出FM算法將運行時間提升到線性運行時間。Karypis等[5]提出并行多層級圖劃分算法,在每一個層級上進行最小二分,進一步縮短了劃分所需的時間。啟發式算法不能保證性能,但是許多啟發式的實現,例如MEITIS[6]、Chaco[7]等,在實際中應用中非常的有效。
由于對目前的大規模圖而言,離線啟發式方法也變得吃力,Stanton和kliot[8]提出一系列不區分無向圖和有向圖的使用啟發式方法的在線流圖劃分方法,簡單提到圖數據流中頂點順序對劃分結果的影響。Fennel[9]結合其他啟發式方法的流劃分框架對該工作進行了擴展。Joel Nishimura和Johan Ugander[10]更進一步提出Restreaming LDG和Restreamig Fennel,使用最近的圖劃分結果來生成初始圖劃分,該方法提升了流圖劃分的結果質量,但卻減慢了劃分速度。平衡圖劃分問題存在一種變形,給每個分區添加了不同的大小限制,稱為非平衡圖劃分,或異構環境中的圖劃分。Ning Xu等[11]提出了一種在異構環境中的流圖劃分方法,Robert Krauth?gamer等[12]提出了非平衡圖劃分。
2 動態反向映射圖
2.1 信息丟失

圖1 有向圖示例
對于無向圖來說可以從一條頂點信息中獲得其所有的鄰居信息,但是對于有向圖,并不能從一條頂點信息中獲取其所有的鄰居信息,現有的流圖劃分算法大都忽略了有向圖的信息丟失問題。舉例來說明,如圖1,從頂點1可以得到其與頂點2,8相連,但是對于流式處理方法來說,當處理到頂點2和8時卻無法得知其與頂點1相連,故而無法準確判斷頂點2和8在各個分區的鄰居數量,這會造成邊信息的丟失,導致不佳的圖劃分結果。但若對全圖遍歷以獲取準確的頂點間邊的信息又會失去流式處理一次遍歷的初衷,增大圖劃分算法的執行時間。
2.2 動態信息補全
本文提出的動態反向映射圖,隨著圖劃分過程的進行,會逐步保存可利用的信息,去除無用信息。動態反向映射圖DG=(DV,DE),其中DV包含已被分配但其鄰居尚未被完全分配的頂點,以及已經被探測到的但尚未被分配的頂點。DE包含原圖數據中的反向邊,因此當分配頂點時,可以在動態反向映射圖中,直接通過當前頂點的單一記錄,得知分配當前頂點可利用的邊和點的信息。
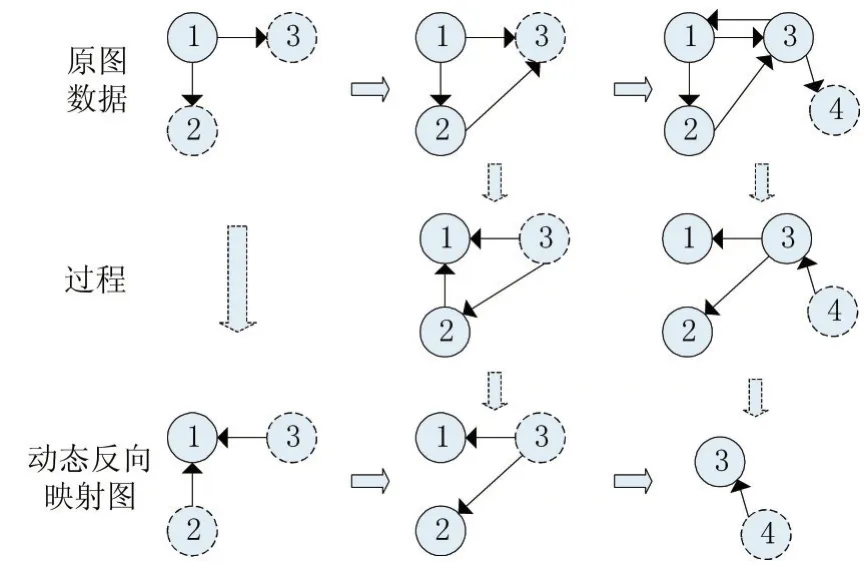
圖2 動態反向映射圖示例
圖中虛線頂點代表尚未分配頂點,實線頂點代表已被分配頂點。
當頂點1到來時,還帶有其鄰居3和鄰居2,但此時并不知道2和3的鄰居,也不知道其鄰居信息什么時間會到來,只能將此條數據反向存儲起來,以備后用。當頂點2到來,帶有其鄰居3,同頂點1的處理方式相同,將2和3反向存儲起來,檢測到此時2已經被分配完畢,所以反向映射圖中的頂點2的出度邊去除,因為在未來的分配過程中將不會再用到反向映射圖中的頂點2的出度邊,以控制作為輔助數據的動態反向映射圖的規模的增長;同理,頂點3到來時,將其與頂點4相連的邊存入動態反響映射圖,同時3的出度邊被去除,而此時頂點1和頂點2已經成為了孤立的頂點,所以也被去除。
2.3 有向圖劃分
流圖劃分的基本框架假定一序列的輸入以及一個單一的裝載器,并且頂點一旦確認分配位置,就不再更改,即是所謂的一次遍歷劃分。但一次遍歷自然會在處理有向圖時產生信息的丟失,故本文在此框架基礎上提出基于動態反響映射圖的流圖劃分算法(SGPD?MG),通過動態反向映射圖來收集起始頂點的部分入度邊并確保無出度頂點不被遺漏。SGPDMG算法是基于頂點的圖劃分算法,輸入序列中的一個元組包括當前頂點以及其鄰居信息,本文使用μ來表示。
傳統的圖劃分算法有兩個輸入,邊集E,頂點集V,流圖劃分算法無法利用這兩個數據輸入,數據輸入變為了G'=(V',E),其中V'為有出度定點的集合,本文的算法就是利用此“不完整”的數據輸入,在不增加圖數據的遍歷次數的前提下,用一次遍歷的方式達到更優的分配效果。
算法1:基于動態反向映射圖的流圖劃分算法(Streaming Graph Partition based on Dynamic inverse Mapping Graph,SGPDMG)輸入:G'=(V',E),分區數k.
輸出:將每一個頂點映射到關聯的分區,M(v)∈[k].
步驟:

2.4 啟發式函數
為了以流式圖劃分的過程達到平衡圖劃分的兩個目標,啟發式函數利用了圖的兩個信息,分別是各個分區的空閑程度,以及當前頂點在各個分區的鄰居數量。顯然,當某個分區的空閑程度越大,鄰居數量越多,將當前頂點分配到該分區的趨勢就越大。由此,Stanton 2013的權重確定性貪心算法(LDG)提出了如下形式的公式:
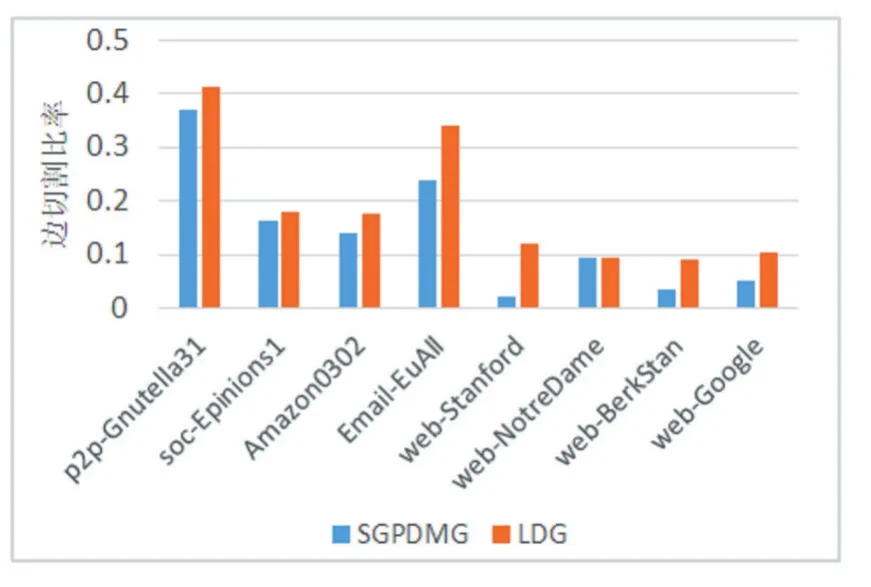
圖3 邊切割比率對比,k=4

其中ind即為當前頂點要分配到的分區的編號,符號Pt代表時間t時的分區集。每一個獨立的分區由Pt(i)表示,所以等于所有已被分配的頂點。v表示在時間t,流中來到的頂點,Γ(v)代表頂點v的所有鄰居,|S|表示集合S中的元素數量,C是每個分區上的容量限制。
3 實驗
有向圖許多都會存在沒有出度的頂點,表1是對實驗圖數據中有出度頂點數目的統計,實驗數據來自于斯坦福大型網絡數據集收集網站[13]。可以看出,有部分圖數據有出度頂點的占比時非常之低的,例如p2p-Gnutella31只有26.18%,而WikiTalk只有6.16%。
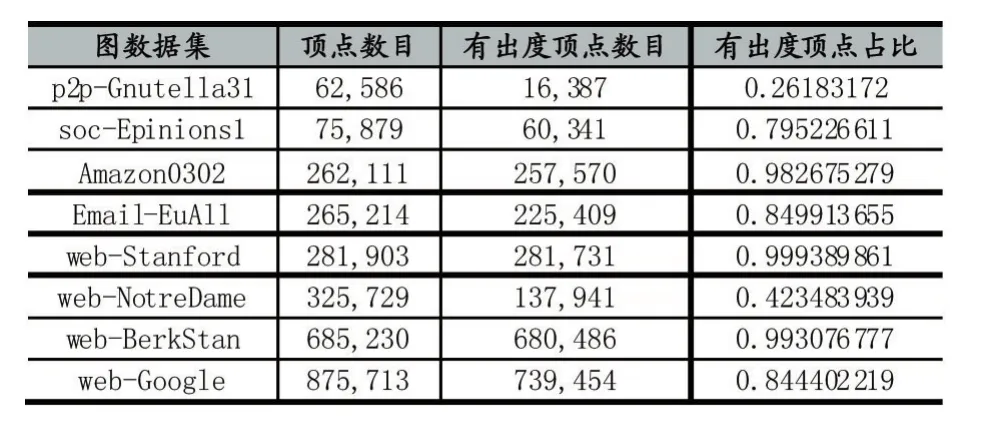
表1 圖數據中有出度頂點與總頂點數對比
圖劃分算法最重要的評價指標是邊切割比率,圖3、圖4和圖5的實驗中可以看出本文提出的算法在不同的k值下,都能取得更好的劃分結果。實驗中效果最好的web-Stanford數據集不是無出度頂點占比最大的數據集,可以看出即便是只有少量的無出度頂點,對其的忽略也有可能產生巨大的結果影響。
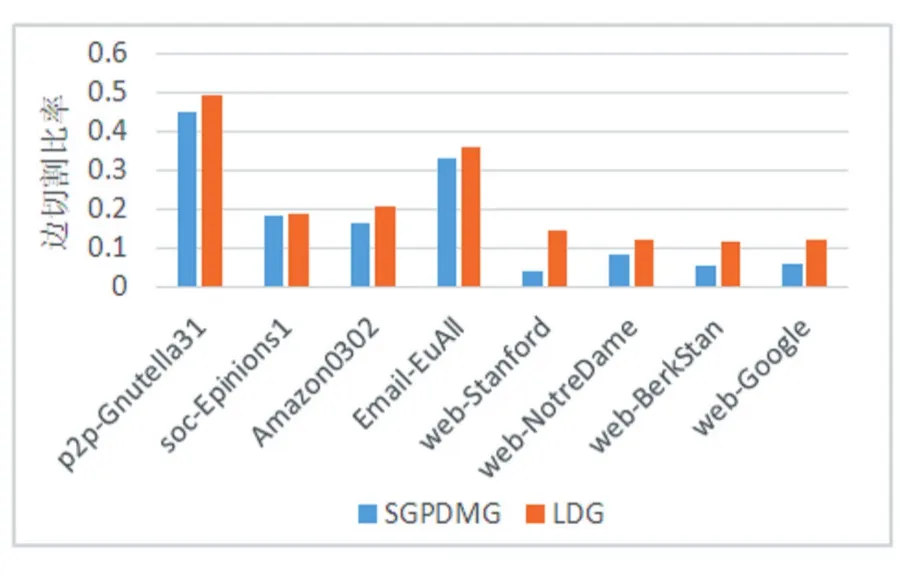
圖4 邊切割比率,k=8

圖5 邊切割比率,k=16

圖6 算法消耗時間對比
算法追求效果的同時,也需要考察其執行時間,圖6的實驗展示了算法的消耗時間,可以看出本文提出的算法在時間消耗上并不處于劣勢。
參考文獻:
[1]L.Hyafil,R.Rivest.Graph Partitioning and Constructing Optimal Decision Trees are PolynomialComplete Problems[R].Technical Report 33,IRIA-Laboratoire de Recherche en Informatique et Automatique,1973.
[2]M.R.Garey,D.S.Johnson,L.Stockmeyer.Some Simplified NP-Complete Problems[C].In 6th ACM Symposium on Theory of Computing,STOC.ACM,1974:47-63.
[3]B.W.Kernighan and S.Lin.An Efficient Heuristic for Artitioning Graphs[J].Bell Sys.Tech.Journal,49:291-308,1970.
[4]C.M.Fiduccia,R.M.Mattheyses.A Linear Time Heuristic for Improving Network Partitions[C].In 19th IEEE Design Automation Conference,1982:175-181.
[5]G.Karypis and V.Kumar.A Fast and High Quality Multilevel Scheme for Partitioning Irregular Graphs[C].In ICPP,1995:113-122.
[6]B.Hendrickson,R.Leland.A Multilevel Algorithm For Partitioning Graphs[J].In Supercomputing,1995.
[7]George Karypis,Vipin Kumar.A Parallel Algorithm for Multilevel Graph Partitioning and Sparse Matrix Ordering[J].Journal of Parallel and Distributed Computing,1998:48(1):71-95.
[8]Isabelle Stanton,Gabriel Kliot.Streaming Graph Partitioning for Large Distributed Graphs[P].In Proc.Of KDD Conference,2012:1222-1230.
[9]Charalampos E.Tsourakakis,Christos Gkantsidis,Boˇzidar Radunovi'c,and Milan Vojnovi'c.Fennel:Streaming Graph Partitioning for Massive Scale Graphs[R].Technical report,Microsoft,2012.
[10]Joel Nishimura,Johan Ugander.Restreaming Graph Partitioning:Simple Versatile Algorithms for Advanced Balancing[P].In Proc.of SIGKDD conference,2013:1106-1114.
[11]N.Xu,B.Cui,L.-n.Chen,Z.Huang,Y.Shao.Heterogeneous Environment Aware Streaming Graph Partitioning[J].TKDE,2015.
[12]Robert Krauthgamer,Joseph(Seffi)Naory,Roy Schwartzz and Kunal Talwarx.Non-Uniform Graph Patitioning[C].Acm-siam Symposium on Discrete Algorithms,2014:1229-1243.
[13]http://snap.stanford.edu/data/index.html

