基于粒子群算法的觀測平臺軌跡優化方法研究

趙琛，李健，師海云

（四川大學電子信息學院，成都 610065）

0 引言

隨著反輻射導彈技術以及電子對抗技術的發展，一些有源探測方法，如雷達等，正在受到威脅。無源定位系統由于其隱蔽性，得到了很好的發展，根據無源定位體制又可以分為時差無源定位系統、測向定位系統、到達頻差定位系統等[1,2]，其中，時差無源定位（TDOA）技術由于其定位精度相對較高、工作頻帶寬、對輻射源頻率未知、快變的情況具有良好的適應性等優勢，受到了研究人員的關注。

在時差無源定位系統中，定位的精度和輻射源與觀測平臺的相對幾何位置有關。目前，大部分研究成果也集中在此方面。其中，文獻[3-6]研究了幾種常見的布站方式的定位精度的差異，并用實驗驗證了基線長度與基線角對精度的影響。文獻[7]用自適應遺傳算法找到靜止目標的最優布站。但上述研究的前提均是目標靜止，而實際情況中，目標運動的情況居多，此時，用目標靜止的方法來進行處理會導致觀測器測量誤差累計增大，最終將對目標失去跟蹤與定位。

針對以上不足，本文提出了一種基于粒子群算法的多觀測平臺軌跡優化方法，將軌跡優化問題轉換為帶各觀測平臺下一時刻的運動方向以及速度調整因子的GDOP的非線性優化問題，并用粒子群算法對該問題進行實時求解，并就最優布站情況對目標進行時差無源定位，將得出的目標位置作為濾波輸入，得到下一時刻目標的預測值，從而進行下一輪的迭代。

1 目標函數的確定

在時差無源定位系統中衡量定位精度的一個重要指標是誤差幾何稀釋度（GDOP）值，它用來描述定位誤差的幾何分布[8]。下面以三站時差定位體系為例，對其GDOP進行推導。

在三站時差定位體系由一個主站——(x0,y0,z0)T和兩個副站——(x1,y1,z1)T、(x2,y2,z2)T構成，輻射源的位置為(xt,yt,zt)T，r0為輻射源與主站的距離，r1和r2分別表示輻射源與兩個副站之間的距離，Δr1和Δr2分別表示兩個副站到輻射源之間的距離與到主站之間的距離的差值。

在三觀測平臺下，理論上只能對觀測平臺所在平面內的輻射源進行定位，但這必然會給定位帶來一定的誤差，為了降低這個系統誤差，可以根據已知條件對輻射源的高度進行合理假設，這里我們將其設為，則定位方程為：

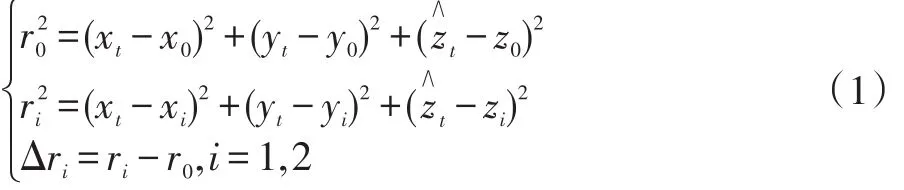
將上式中的最后一個等式兩邊進行微分：

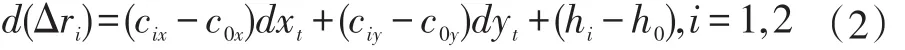
其中：

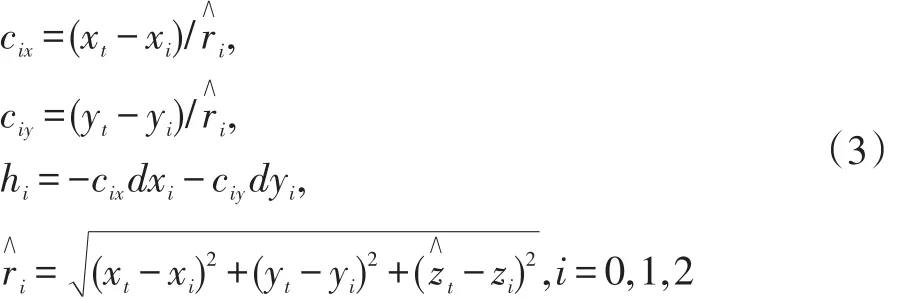
令：

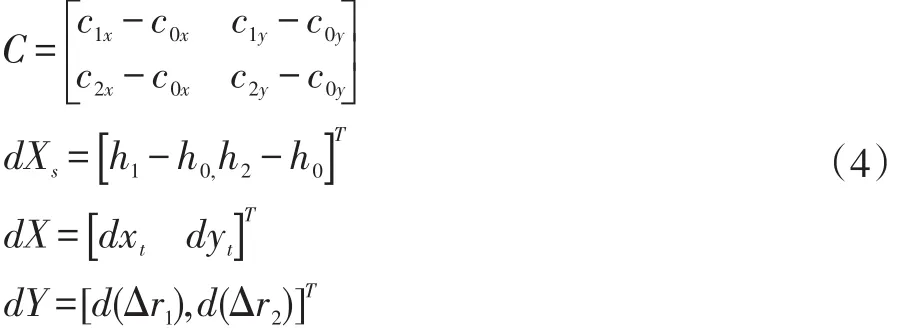
（2）式可寫作：

用偽逆法求解得dX得：

令：

其中，dX表示輻射源的定位精度，dY表示距離差的測量誤差。

設Δri經系統修正以后均值為0，dXs個元素互不相關，則定位誤差的協方差為：

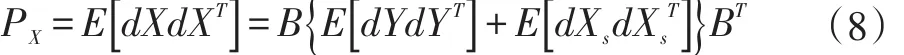
有：

設觀測器載體的最大飛行速度為V，速度調整因子為ai,航向角為θi（i=0,1,2）,則 k 時刻的觀測器坐標為：

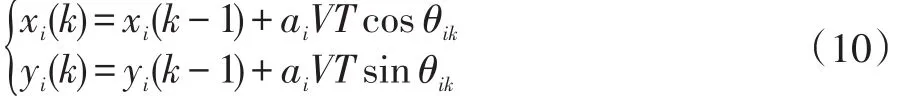
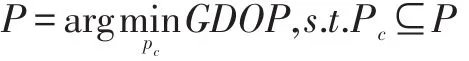
其中P為優化后的參數集，Pc表示任意時刻的解空間的集合。

2 求解軌跡優化問題的粒子群算法

粒子群優化算法（PSO）由Eberhart博士和Kenne?dy于1995年提出，是一種群體智能算法，源于鳥類覓食的靈感，粒子群算法利用群體中的個體對信息的共享使整個群體的運動在問題求解空間中產生從無序到有序的演化過程，從而獲得最優解。它是群體智能算法中最簡單的一種，具有精度高、收斂快等優點，這些優點非常適用于實時性強的問題。

對于三平臺軌跡優化問題，將帶求解的參數個數設為6，分別為這三個平臺的航向角以子i當前飛行速度，pi是使得粒子i具有最好適應度的位置，pg為所有粒子中出現的最好的適應度對應的位置。在該問題中，適應度最好意味著當前位置下的GDOP值最小。第i個粒子在6維空間中的速度與位置的更新公式如下：

其中i∈(1,2,???,n),d∈(1,2,???,6)，w 為慣性權重，c1、c2位學習因子，pid為每個粒子到目前為止出現的最佳位置，pgd為所有粒子到目前為止所出現的最佳位置。

3 軌跡優化與目標估計

傳統輻射源被動跟蹤中，由于輻射源運動軌跡不定，而觀測平臺始終以固定的布站運動會導致測量誤差逐漸積累，最終出現失跟的可能，為了減少濾波發散的影響，將軌跡優化加入到整個目標的被動跟蹤過程中，使其成為一個閉環的過程，減少布站對精度的影響。

整個輻射源被動跟蹤過程如下：

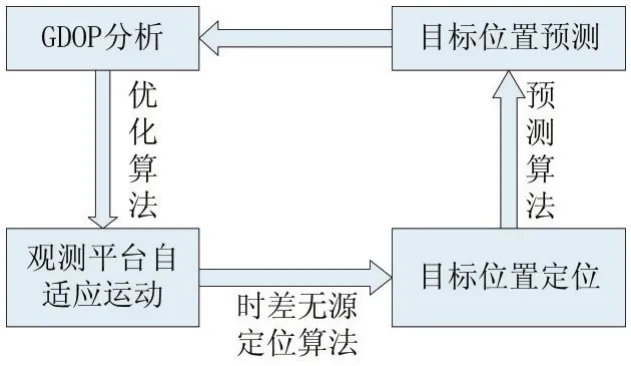
圖1 輻射源被動跟蹤過程

4 仿真實驗與結果分析

4.1 仿真實驗

在三平臺二維空間中完成，測量時間間隔T=1s，到達時間測量精度設為20ns（對應的輻射源到副站與到主站之間的距離精度為6m，三個觀測器以到三角形編隊（基線夾角為 120°），三平臺的初始位置為：（0,0,9），（13,7.5,9），（-13,7.5,9）（單位是 km）目標輻射源的初始位置為：（0,200,9.6）（km），考慮到信號可靠傳輸的影響，將主站與副站的距離限制在20公里內。同時，考慮到機載平臺的機動性，將機載平臺每時刻的轉彎幅度定其上一狀態的方向的±45°之間。對以下幾種情況進行仿真（單位均為km/s）：

場景 1：輻射源速度為（0.2,-0.2）（km/s），觀測器自適應運動。

場景2：輻射源在x方向速度為0.2km/s，在y方向初始速度為0.1km/s，加速度為0.001km/s2，即運動軌跡為拋物線形式，觀測器自適應運動。

將以上兩種情況與觀測器按（0.2,-0.3）（km/s）的速度以固定軌跡運動做比較。

4.2 實驗分析

圖2中，左側為用粒子群算法對觀測器軌跡的實時優化圖，藍色線條為觀測器軌跡，紅色代表目標運動軌跡。可以看到，在基線長度未到達最大時，副觀測器遠離主觀測器，使基線距離增大，該運動軌跡符合預期，當基線距離接近限定長度時，三觀測器逐漸減小與目標之間的距離，最后當觀測平臺與目標處于精度較高的布站形式時，觀測器將保持此狀態，即盡可能使目標處于以副觀測器連線為底邊的等腰三角形的中垂線上。在圖2的GDOP圖中，藍色曲線代表觀測器軌跡實時優化后的GDOP圖，黑色軌跡代表觀測器按固定軌跡飛行時的GDOP圖，經過軌跡優化后的目標跟蹤精度明顯高于按固定軌跡飛行時的跟蹤精度。

圖3中，左側為用粒子群算法對觀測器軌跡的實時優化圖，藍色線條為觀測器軌跡，紅色代表目標運動軌跡。可以看到，其觀測器軌跡優化曲線與圖2中大致相同，只是GDOP圖略有差異，這是因為目標在y軸上做勻加速運動，而在某一時刻，目標的運動速度超過了觀測器的最大速度，此時，觀測器無法繼續保持最優布站形式，所以GDOP圖中的后半段的值有所上升，符合實際情況。

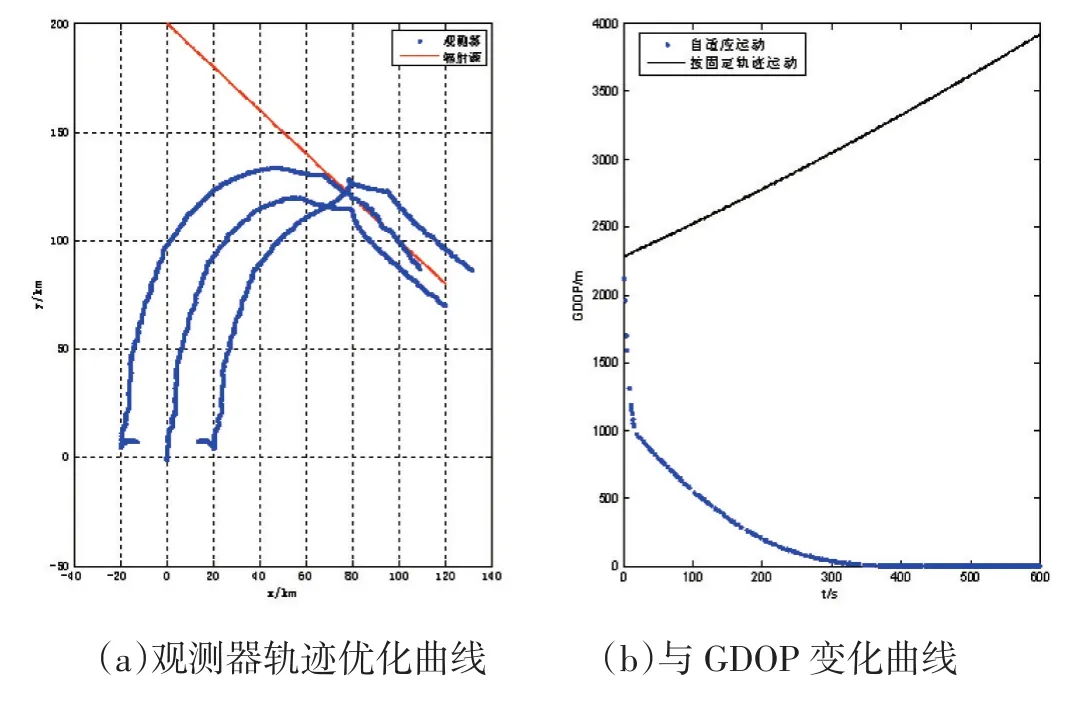
圖2

圖3

注：在觀測器按固定軌跡飛行時，其在x軸上的速度與目標一致，而目標在y軸的初始速度比觀測器低，其位置差會增加，所以在一段時間內對應的GDOP曲線呈上升趨勢；當目標在y軸上的速度高于觀測器速度時，其位置差會減小，GDOP呈下降趨勢；當后期目標逐漸遠離觀測器時，GDOP值又會逐漸變大。

以上兩種實驗場景證明，用粒子群算法對觀測平臺進行實時軌跡優化是有效的，在觀測器速度允許的情況下，可以對輻射源保持高精度的定位追蹤，該方法相較于固定形式布站，有明顯的優勢。

5 結語

本文在時差無源定位體制下，對目標運動的情況，提出了一種基于粒子群算法的觀測平臺軌跡優化方法。將軌跡優化加入到目標被動跟蹤的過程中，避免了濾波發散，滿足了定位精度的要求。仿真結果證明，該方法作用下的定位跟蹤精度明顯高于觀測器沿固定軌跡飛行時的跟蹤精度。

參考文獻：

[1]孫仲康，周一宇，何黎星.單多基地有源無源定位技術.北京：國防工業出版社，1996.5

[2]單月暉，孫仲康，皇甫堪.不斷發展的無源定位技術.航天電子對抗2002（3）:36-42

[3]Martinescalona I,Barceloarroyo F.Impact of Geometry on the Accuracy of the Passive-TDOA Algorithm[J].2008:1-6.

[4]Musicki D,Kaune R,Koch W.Mobile Emitter Geolocation and Tracking Using TDOA and FDOA Measurements[J].IEEE Transactions on Signal Processing,2010,58（3）:1863-1874.

[5]王瀚.機載多平臺時差無源定位系統若干關鍵技術研究[D].國防科學技術大學,2006.

[6]楊麗麗,孫曉聞.無人機載多站無源定位系統精度分析[J].中國電子科學研究院學報,2014,9（4）:348-352.

[7]潘燁煬,郭潔,張林穎,等.基于自適應遺傳算法的優化布站方法研究[J].國外電子測量技術,2013,32（6）:62-64.

[8]B DSivazlian and R E Green.Effect of Instrument Siting and Coordinate Selection on GDOP in Target Tracking.AD/A-03183.