基于高斯徑向基函數(shù)網絡的潛在剖面建模方法

黎鳴

（四川大學計算機學院，成都 610065)

1 潛在剖面分析

近年來，潛在變量建模（潛在結構分析，Latent Vari?able Modeling，Latent Structural Analysis）越來越受到醫(yī)學生物、社會心理等學科的重視，其原因在于，一方面，它能通過潛在變量的概念來表示外顯變量（因變量）所蘊含的抽象且無法直接觀察的內部關系，另一方面，傳統(tǒng)的顯變量分析方法的有效性正逐漸受到數(shù)據復雜性的影響，研究者搜集到的數(shù)據越來越底層、復雜、交錯、實時，這些數(shù)據的潛在關系很難再通過簡單的轉換方法得到。而潛在剖面分析（LPA）作為一種對內部因素間交互進行建模的方法，其有效性在醫(yī)學生物、社會心理等學科領域已經得到大量的證實。LPA是一種以人為中心的潛在變量建模方法，其基本假設在于因變量間存在有意義的、共同的模式（Pattern），而這種假設與類型學（Typology）等多個研究領域所用的假設相仿[1]。由于其假設也包含了因變量間存在的結構化關系，因此，LPA也被作為一種結構化（Structural）的建模方法。

按照外顯變量與潛在變量的數(shù)據類型（連續(xù)或離散），潛在結構分析可以分為四類，即：外顯離散且潛在離散的潛在類別分析（Latent Class Analysis），外顯連續(xù)但潛在離散的潛在剖面分析（Latent Profile Analysis），外顯離散但潛在連續(xù)的潛在特質分析（Latent Trait Analysis），以及外顯連續(xù)且潛在連續(xù)的因素分析（Fac?tor Analysis）[2]。可以說，潛在結構分析是傳統(tǒng)因素分析的發(fā)展與擴展，與傳統(tǒng)因素分析一同建立了一個完整的潛在分析方法框架。

潛在類別分析（LCA）與潛在剖面分析（LPA）都是基于貝葉斯統(tǒng)計理論的一種，LCA為無參估計，LPA為有參估計，都采用了“屬性條件獨立性假設”（Attribute Conditional Independence Assumption），即對已知的顯變量，假設所有屬性相互獨立。對于一個具有M個屬性、K個潛變量的LCA的模型，其貝葉斯判別公式如公式

由于LPA與LCA的區(qū)別主要在外顯變量是否連續(xù)這一點上，因此，當外顯變量為連續(xù)的時候，貝葉斯決策假設外顯變量服從于多個同構的潛在分布，通常假設該分布為正態(tài)分布。因此，屬于潛在類別k并且具有顯變量模式x的聯(lián)合概率密度函數(shù)p可以表示成公式（2）的形式[3-4]：

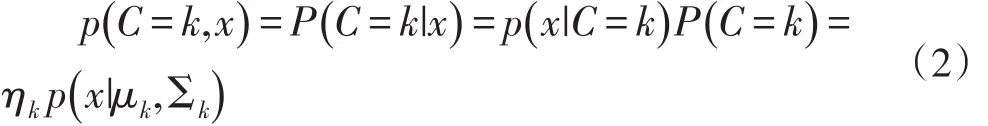
其中，p是服從均值μ、協(xié)方差陣為Σ的正態(tài)分布的概率密度函數(shù)，各個潛在分布通常假設均值為0，協(xié)方差可以相同也可以不相同。ηk為潛在類別概率（La?tent Class Probability），即為前文所述的先驗概率；這時候的被稱為類條件概率密度（Class-Condi?tional Probability Density）。不同于LCA的無參估計過程，LPA通常采用基于期望最大化（EM）的最大似然法（MLE）估計假設分布的參數(shù)，由于LPA通常僅需要得到估計的分布參數(shù)，因此，在LPA應用領域又通常將該模型稱為貝葉斯回歸模型或貝葉斯聚類模型[5]。由于在現(xiàn)實問題中，屬性條件獨立性假設通常很難成立，通過對屬性條件獨立性假設進行放寬，由此可以得到一類稱為“半樸素貝葉斯分類器”（Semi-Na?ve Bayes Clas?sifier）的學習方法，該類方法可以建模顯變量屬性間的關系。也可以通過建立貝葉斯網絡（信念網，Bayesian Network，Belief Network），借助有向無環(huán)圖來刻畫屬性間的關系[6]。

LPA基于貝葉斯分類器的原理，同樣獲得了很好的顯變量分類（聚類）能力。雖然LPA解決了從顯變量（因變量）到潛變量的轉化過程，但是，大部分研究仍然希望得到的是自變量與顯變量之間的關系。為此，通常做法是直接使用現(xiàn)有的分類方法建立自變量與潛變量之間的分類模型，藉由潛變量模型得到顯變量結果。這種兩段式的訓練方式，找到的都是局部最優(yōu)的模型，而不是自變量（特征）與顯變量之間關系的最優(yōu)模型，因此，通常由此推斷的自變量與顯變量之間的解釋度（擬合優(yōu)度）都很低，現(xiàn)有文獻都規(guī)避自變量與顯變量之間的關系，而提出以“人”（潛變量）為中心的判別方式，忽視了模型的最終應用目的。

2 徑向基函數(shù)網絡

徑向基函數(shù)（RBF）網絡（Radial Basis Function Net?work）是一種以徑向基函數(shù)為隱藏層神經元節(jié)點的前饋神經網絡，是一種連接主義的模型。神經網絡的有效性在神經科學領域和計算機領域均得到了大量的證明，它由具有適應性的簡單單元組成廣泛并聯(lián)的網絡，是對生物神經系統(tǒng)的模擬，而前饋神經網絡（層間全連，層內不連）是最基本的一種神經網絡結構[6]。RBF網絡是一種非線性局部逼近網絡，能逼近任意的非線性函數(shù)，具有良好的泛化能力，同時，仍具有較好的解釋性。其網絡結構通常圖1所示：

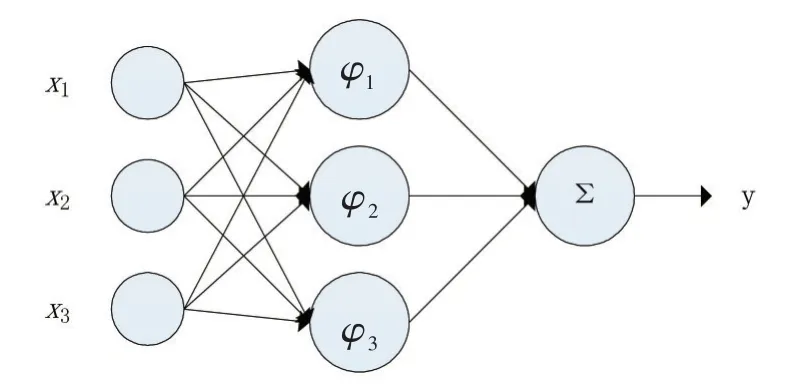
圖1 RBF網絡結構

其中x為輸入向量，xi為第i個屬性（特征），x所在的神經元節(jié)點為輸入層；φ為高斯徑向基函數(shù)，其公式可以定義為公式Eq.3的形式，φ所在的神經元節(jié)點為隱藏層，φj為第j個神經元的高斯徑向基函數(shù)；Σ為求和函數(shù)，Σ所在的神經元節(jié)點為輸出層；y為網絡的輸出。

RBF網絡可以理解為：輸入層是網絡與外界環(huán)境的連接，隱藏層是輸入空間到隱藏空間之間的變換，輸出層是網絡的響應。高斯函數(shù)φ在統(tǒng)計學文獻中廣泛的解釋為核（Kernel），因此RBF網絡是一種類似于核回歸的核方法（模型）[7]。該網絡的訓練方式通常采用兩段訓練（2-Stage Training）的方式：第一階段，使用非監(jiān)督（Unsupervised）學習的訓練方式尋找高斯徑向基的中心樣本，第二階段，使用監(jiān)督（Supervised）學習的訓練方式訓練網絡參數(shù)。

RBF網路與LPA方法具有極高的相似性，從LPA的方向解釋，x即為自變量（特征），φ為潛變量的概率密度函數(shù)，y為顯變量，將Σ替換為采樣函數(shù)，則該網絡即為RBF-LPA網絡。其訓練方式也采用兩段訓練的方式，第一階段，使用LPA樸素貝葉斯回歸的方法，確定高斯徑向基的概率參數(shù)，第二階段，使用傳統(tǒng)的BP方法訓練整個網路的參數(shù)。

3 結語

本文給出了一種基于RBF的LPA方法，該方法綜合考慮了如何將LPA直接用于全局建模。雖然該思想結合了LPA易解釋，RBF效果好的優(yōu)點，但是，后續(xù)需要更多實際的應用來證明該方法的有效性，以及從定義上給予更嚴格的證明。

參考文獻：

[1]Ferguson S,Hull D.Personality Profiles:Using Latent Profile Analysis to Model Personality Typologies[J].Personality&Individual Differences,2018,122:177-183.

[2]邱皓政.潛在類別模型的原理與技術[M].北京大學出版社,2008.

[3]RichardO.Duda,PeterE.Hart,DavidG.Stork.模式分類[M].機械工業(yè)出版社,2003.

[4]孫即祥.現(xiàn)代模式識別[M].國防科技大學出版社,2002.

[5]趙麗,李麗霞,周舒冬,等.潛在剖面分析和系統(tǒng)聚類法比較的模擬研究[J].廣東藥學院學報,2013,29(2):206-209.

[6]周志華.機器學習[M].清華大學出版社,2016.

[7]SimonHaykin,海金,Haykin.神經網絡與機器學習[M].機械工業(yè)出版社,2009.