橋墩承臺對高架橋下路面不均勻沉降的影響

張 玉 張 峰 肖 昊 鄭立斐

(1.河南交院工程有限公司 鄭州 450000； 2.中交第二公路勘察設計研究院有限公司 武漢 430000； 3.華中科技大學土木工程與力學學院 武漢 430074)

近年來，建設高架橋成為改善交通狀況的有效措施。在高架橋運營過程中，橋下路面大量出現不均勻沉降，嚴重影響交通通行，同時還存在諸多安全隱患。路面不均勻沉降引起路基整體性變差，路基整體或部分下沉，路面開裂破壞，導致行車舒適度降低，阻礙車速，影響交通流量[1-2]。因此，分析和研究承臺對高架橋下橋墩間路面不均勻沉降的影響，并提出合理化的建議是十分必要的。

1 數值分析模型的建立

為了更準確地模擬高架橋下橋墩間的路面變形情況，建立三維模型進行有限元分析，模型中的高架橋橋墩采用單墩形式，整個模型中共有3跨，每跨的跨度30 m，橋墩高15 m，承臺的高度為3 m，承臺下的樁基長45 m，高架橋下的路面寬度為40 m。

為簡化數值分析模型，省去橋面板，將橋面板上的荷載等效施加在橋墩上，采用midas GTS NX有限元分析軟件進行模擬分析，數值分析模型見圖1。

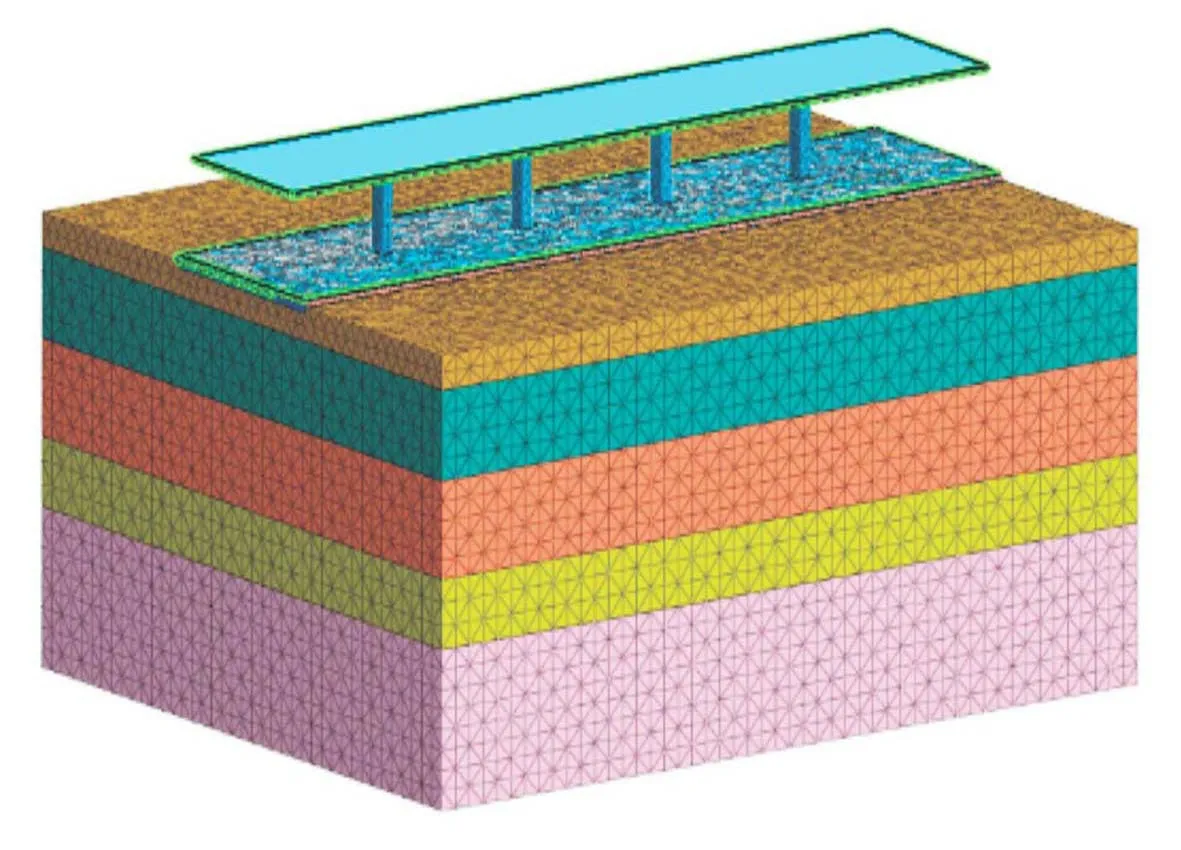
圖1 數值分析模型

1.1 材料本構關系

1) 地基土。采用midas GTS NX中所提供的修正莫爾-庫倫本構模型，適用于各種類型的地基，特別適用于像砂土或混凝土類具有摩擦特性的材料。

2) 路面結構層、高架橋承重構件。采用彈性材料模型，這種模型適用于小應變分析，能夠在一定的簡化條件下模擬結構層的力學性質，通過彈性模量、泊松比、重度等參數來定義材料屬性。

1.2 計算參數的選取

該模型中具體的參數見表1和表2。

表1 土體計算參數表

注：h-厚度；γ-重度；E50ref-三軸試驗割線模量；Eoedref-主壓密加載試驗的切線模量；Eurref-卸載再加載模量；μ-泊松比；e0-初始孔隙比；n-孔隙率；φ-內摩擦角；c-黏聚力。

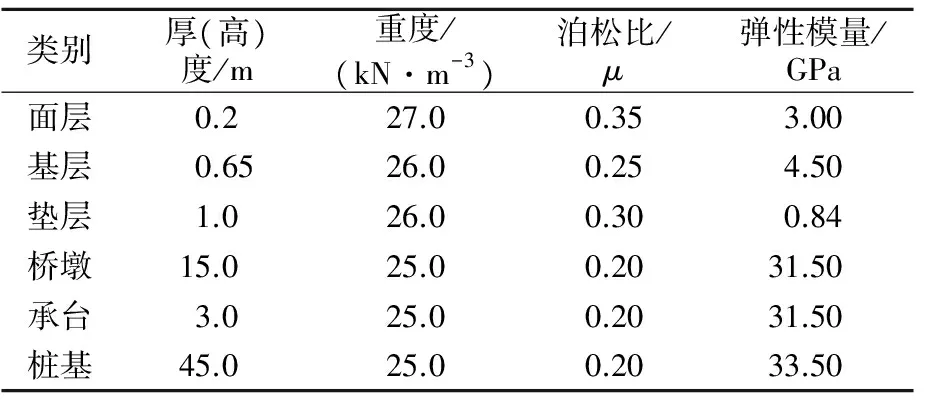
表2 結構構件的計算參數表

2 承臺埋深H對路面不均勻沉降的影響

采用上述的模型及計算參數進行建模模擬，采用的承臺埋深是以路面面層為基準進行計算[3]，模型的埋深分別為H=0.2，0.85，1.35，1.85，2.35，2.85 m。計算中坐標軸方向規定如下：X方向為水平方向，且垂直于行車方向，將其定義為道路的橫向方向；Y方向為另外一個水平方向，且平行于行車方向，將其定義為道路的縱向方向；Z方向為豎直方向，以豎直向上為正。

2.1 橫向路面沉降變化

不同承臺埋深時路面沉降橫向剖面云圖略，將其中特征數值匯總如表3所示。

表3 不同承臺埋深下橫向路面沉降值匯總表

由表3可見：

1) 道路在承臺處相對凸起，在道路兩側相對凹陷。

2) 當承臺的埋深深度不同時，承臺的沉降值都很小，數值相差不大，相對于路面的沉降值，承臺的沉降值變化可以忽略不計。

3) 隨著承臺的埋深增加，承臺周圍的路面和道路兩側的路面的沉降值均增大，但二者的沉降差值有略微降低的趨勢，當承臺埋深在1.85～2.35 m時，路面的沉降差降低較明顯，但整體變化不明顯。

2.2 縱向路面沉降變化

承臺不同埋深下，路面沉降縱向剖面云圖略。

將其中特征數值匯總如表4所示。

表4 不同承臺埋深下縱向路面沉降值匯總表

由表4可見，當承臺的埋深深度不同時，承臺的沉降值都很小，數值相差不大，相對于路面的沉降值，承臺的沉降值變化可以忽略不計。

將表4中的路面沉降差的數值點畫成曲線圖，如圖2所示。

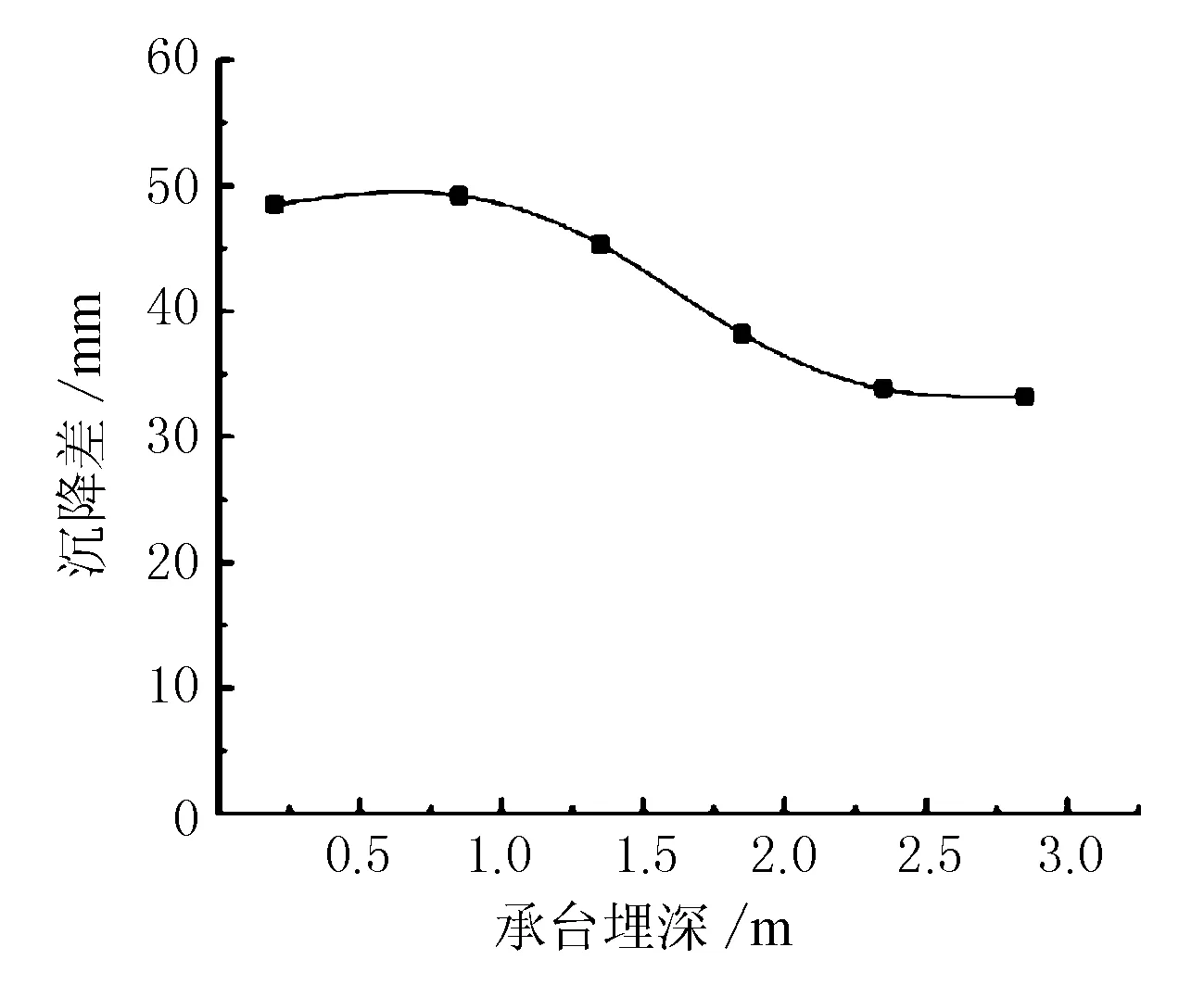
圖2 路面沉降差與承臺埋深關系圖

根據圖2中的變化趨勢可以看出。

1) 隨著承臺埋深增加，路面沉降差逐漸減小。

2) 當承臺的埋深小于1 m時，隨著承臺埋深增加，路面沉降差的遞減變化不明顯。

3) 當承臺埋深在1～2.5 m時，隨著承臺埋深增加，路面沉降差遞減變化顯著，差值減小幅度較大。

4) 當承臺埋深超過2.5 m時，隨著承臺埋深增加，路面沉降差遞減變化不明顯。

3 承臺與路面的相對剛度K對路面不均勻沉降的影響

3.1 承臺與路面的相對剛度K

路面的剛度是指道路在車輛荷載作用下，受力影響范圍內，路面沉降變形區域的抗變形能力。沿著路面橫向或縱向分析，路面不同區域，路面與公路構筑物之間的剛度差異十分明顯，在同一外力的反復作用下，路面產生不同的變形量，必然會引起非常明顯的沉降差異，導致路面破壞，無法保持其正常使用功能[3]。

橋涵結構物一般采用鋼筋混凝土結構，具有較大的剛性，不易發生沉降和變形。但是對于鋪筑在高架橋承臺附近處的路面而言，一般采用瀝青混凝土等材料鋪筑，屬于半剛性或柔性結構，容易產生壓縮沉降。當高架橋建成，橋下路面通車后，隨著時間的推移和車輛及自身重力荷載的影響，路面及高架橋承臺處的填土密實度增大，孔隙率降低，結構層之間被壓縮，而橋梁承臺由于本身的剛度大，因此產生的沉降變形相對于橋下路面小很多，可以忽略不計[4]。久而久之，當路面與承臺的相對沉降差超過一定程度時，瀝青混凝土路面就會出現沉降或斷裂，兩者之間形成錯臺，便會在承臺附近處出現“跳車”現象[5-6]。

一般認為，“剛度”就是物體在外力作用下抵抗變形的能力，是物體在外力作用下應力-應變關系的表征，在工程上一般采用彈性模量來衡量結構或構件的剛度。為減小承臺與路面的相對剛度，采取增加路面剛度方式進行模擬分析。模型中承臺的埋深取2.35 m，路面的彈性模量分別取3，5，10，15，20，25 GPa。

3.2 橫向路面沉降變化

圖3為不同路面彈性模量時，路面沉降橫向剖面云圖。

圖3 不同路面彈性模量下路面沉降橫向剖面云圖

由圖3可見，道路在承臺處相對凸起，在道路兩側相對凹陷。隨著路面的彈性模量的增加，承臺周圍的路面沉降變化不大，但是道路兩側的路面的沉降值均逐漸降低，二者的沉降差值減小較明顯。將特征點處沉降數值匯總如表5所示。

表5 不同彈性模量下橫向路面沉降值匯總表

由表5可見，當路面的彈性模量變化時，承臺的沉降值都很小，數值相差不大，相對于橫向路面的沉降值，承臺的沉降值變化可以忽略不計。

將表5中的橫向路面沉降差的數值繪制成曲線圖，如圖4所示。

由圖4可見：

1) 隨著路面彈性模量的增加，橫向路面的沉降差逐漸減小。

2) 當路面的彈性模量小于5 GPa時，隨著路面的彈性模量的增加，橫向路面的沉降差的遞減變化不明顯。

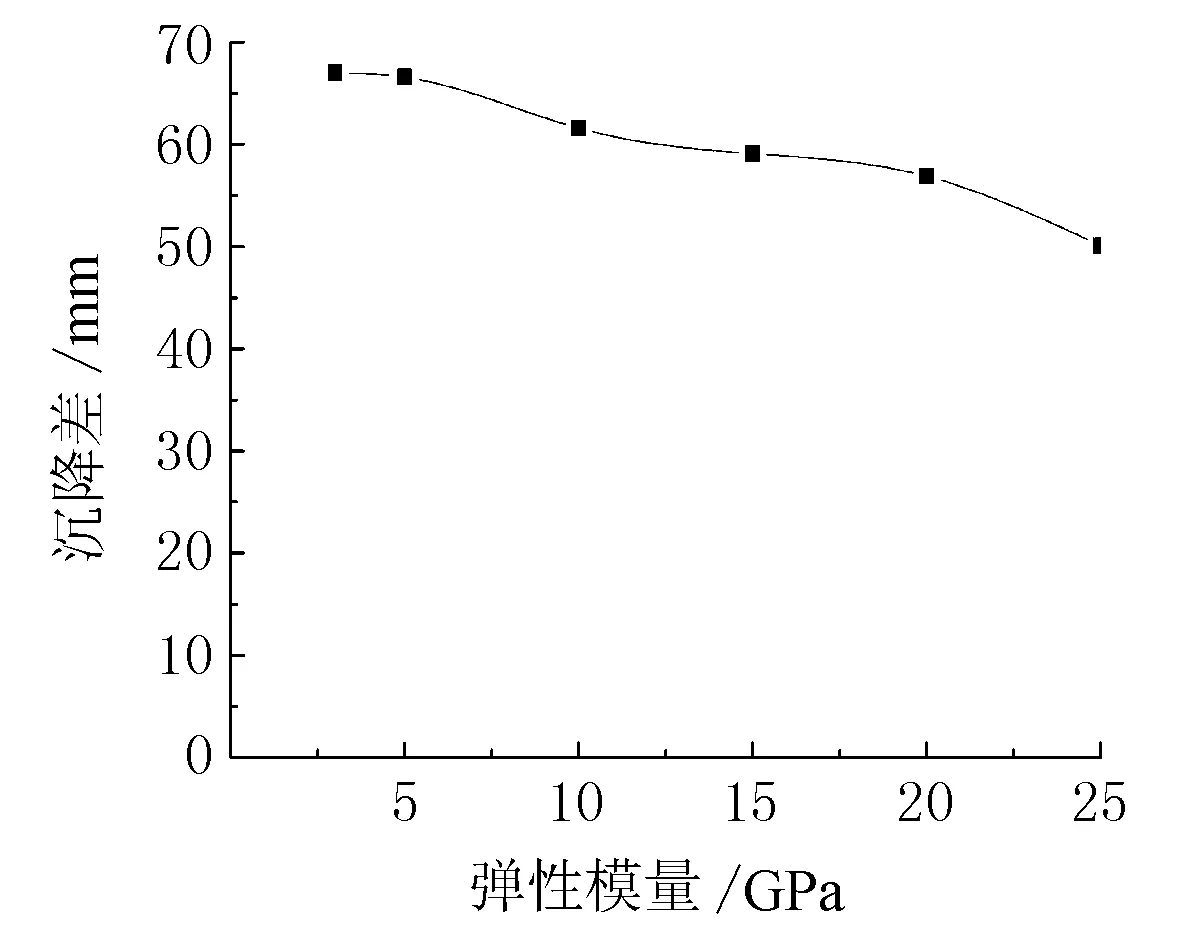
圖4 橫向路面沉降差與彈性模量關系圖

3) 當路面的彈性模量在5～15 GPa時，隨著路面的彈性模量的增加，橫向路面的沉降差遞減變化顯著，遞減的速率較大，差值減小幅度也較大。

4) 當路面的彈性模量超過15 GPa時，橫向路面的沉降差的遞減速率逐漸減小，但是橫向路面的沉降差值仍在減小。

3.3 縱向路面沉降變化

圖5為不同路面彈性模量時，路面沉降縱向剖面云圖。

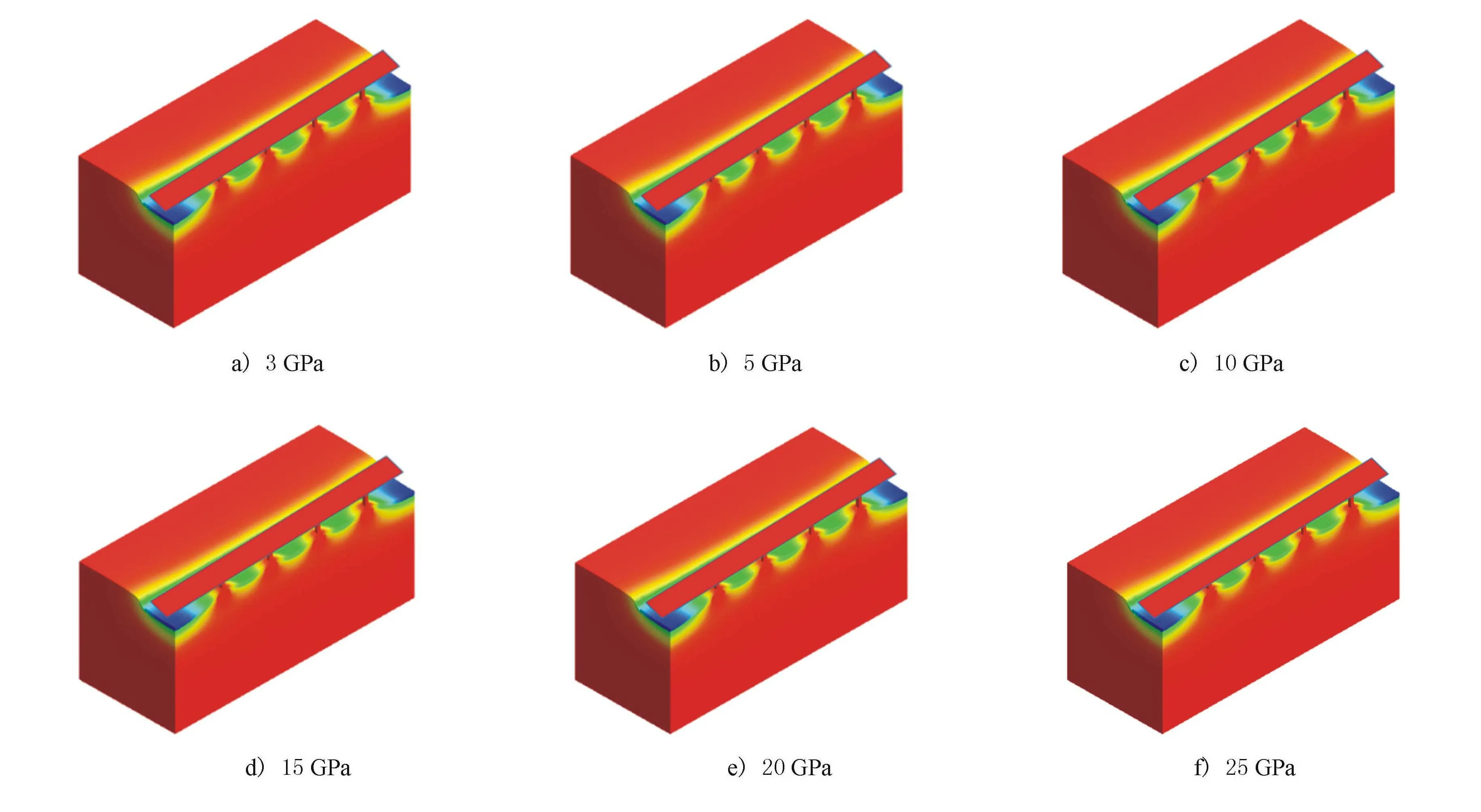
圖5 不同路面彈性模量下路面沉降縱向剖面云圖

由圖5可見，隨著路面的彈性模量增加，路面的“波浪形”變化幅度削弱，即表明路面的沉降差值逐漸減小，同時道路的整體沉降值也在減小。將圖特征點處沉降數值匯總如表6所示。

表6 不同彈性模量時，縱向路面沉降值匯總表

由表6可見，當路面彈性模量增加時，承臺的沉降值逐漸增大，但數值增加不大。而且相對于縱向路面的沉降值，承臺的沉降值變化基本可以忽略不計。

將表6中的縱向路面沉降差的數值點繪制曲線圖，如圖6所示。

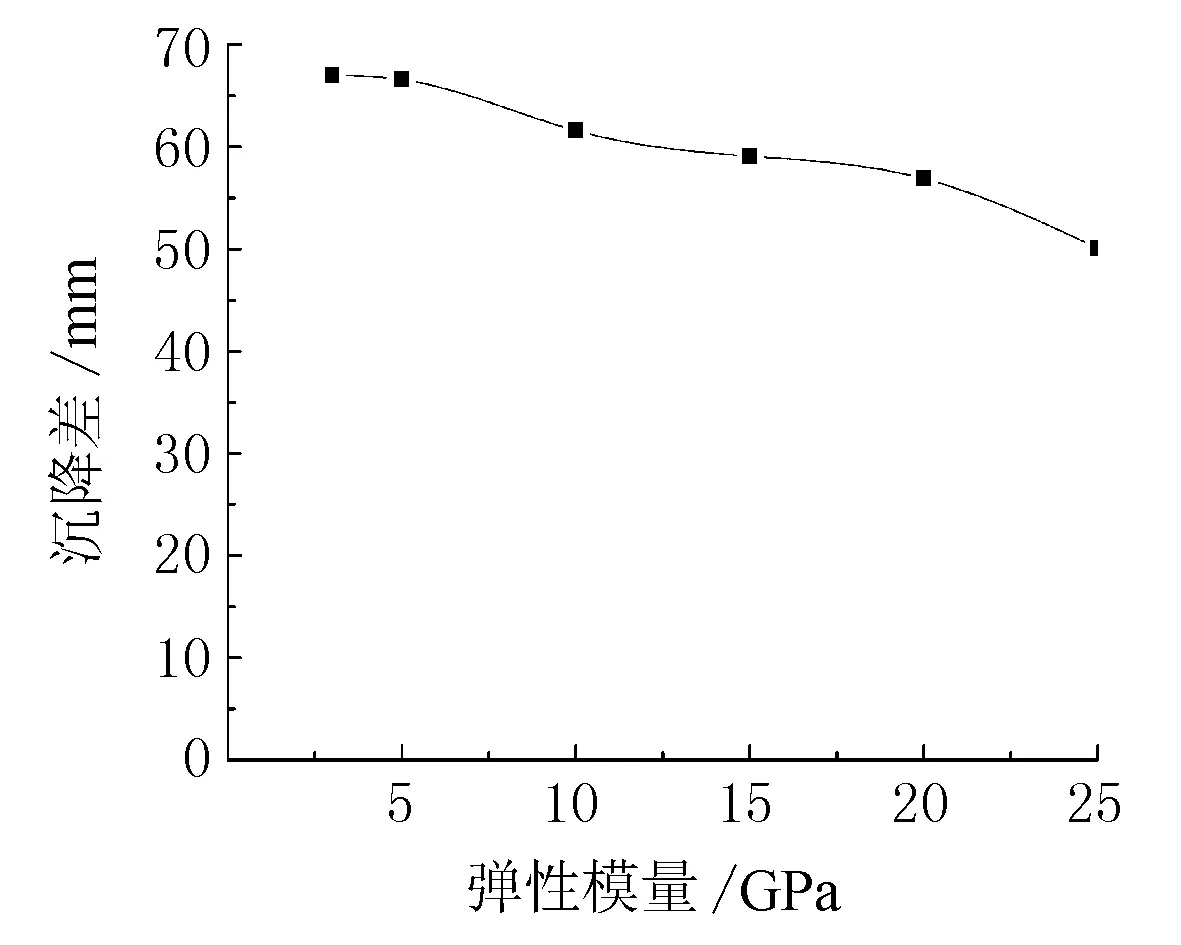
圖6 縱向路面沉降差與彈性模量的關系圖

由圖6可見：

1) 隨著路面彈性模量的增加，縱向路面的沉降差逐漸減小，而且縱向路面沉降差的數值小于橫向路面沉降差的數值。

2) 當路面的彈性模量小于5 GPa，隨著路面彈性模量的增加，縱向路面的沉降差的遞減變化不明顯。

3) 當路面的彈性模量在5～15 GPa時，隨著路面彈性模量的增加，縱向路面的沉降差遞減變化顯著，遞減的速率較大，差值減小幅度也較大。

4) 當路面的彈性模量超過15 GPa時，縱向路面沉降差的遞減速率逐漸減小，但路面的沉降差值仍在減小。

4 結語

利用midas GTS NX建立高架橋與地基路面的三維模型進行有限元計算，承臺對路面不均勻沉降的影響主要表現在以下兩方面。

1) 當承臺的埋深小于1 m時，隨著承臺的埋深增加，路面沉降差逐漸減小，但減小的幅度不明顯。當承臺的埋深在1～2.5 m時，隨著承臺的埋深增加，路面的沉降差也逐漸減小，并且減小幅度較大。當承臺的埋深超過2.5 m時，隨著承臺的埋深增加，路面的沉降差逐漸減小，但減小的幅度也不明顯。

2) 路面的沉降差隨路面彈性模量的增加而遞減，當路面彈性模型小于5 GPa，路面的沉降差的遞減變化不明顯。當路面的彈性模量在5～15 GPa時，道路的沉降差遞減變化顯著，遞減的速率較大，差值減小幅度也較大。當路面彈性模量超過15 GPa時，道路沉降差的遞減速率逐漸減小，但沉降差值仍在減小。

3) 為減小路面的沉降差和節約施工成本，根據具體工程概況，可將承臺的埋深控制在1～2.5 m內。

4) 減小承臺與路面的相對剛度，即提高路面的剛度可有效減小路面的沉降差，針對此因素，可采用混凝土剛性路面以減小路面的沉降差。

[1] 楊友國.公路橋梁沉降段路基路面的施工技術研究[J].黑龍江交通科技,2013(8):77-78.

[2] 張宏光,謝永利.楔形柔性搭板模型試驗[J].長安大學學報(自然科學版),2005,25(3):54-57.

[3] 錢坤,尹新生,朱珊.上部結構剛度對地基不均勻沉降的影響與分析[J].吉林建筑大學學報,2009,26(3):11-14.

[4] 俞永華.路橋過渡段差異沉降處治技術研究[D].西安:長安大學,2004.

[5] 鄧育林,雷凡,何雄君,等.承臺結構形式變化對大跨斜拉橋抗震性能的影響分析[J].武漢理工大學學報(交通科學與工程版),2013,37(4):839-842.

[6] 牛思勝.黃土地區臺后跳車柔性搭板處治技術研究[D].西安:長安大學,2006.