基于多視圖矩陣分解的聚類分析

張祎 孔祥維 王振帆 付海燕 李明

在計算機視覺和模式識別領域,輸入數據的維數過高會增加計算的復雜度,使得對數據的處理變得困難.為了降低數據的維數,通常采用矩陣分解的方法.矩陣分解的方法將數據矩陣分解成多個矩陣的形式,其中一個矩陣可以很好地逼近原始矩陣,在保留原始信息的條件下,同時可以從高維到低維的映射,學習更好的特征描述方法.這樣這種矩陣分解的方法有多種,如SVD(Singular value decomposition)、QR 分解、NMF(Nonnegative matrix factorization)等.

NMF可以將原始數據分解為基矩陣和系數矩陣的乘積.基矩陣的作用類似人臉的各個不同局部塊的描述,系數矩陣為原始數據在這些基向量的線性組合的權重.對于給定的數據矩陣X,在學習到對應的基矩陣U之后,對應的系數矩陣V便可以描述原始矩陣.最近的研究表明,NMF在人腦識別等領域已經超過基于SVD的方法[1?3].

雖然單視圖的NMF提高了原始數據的有效性,但是圖像可以從不同的視圖進行描述.這些視圖可以是不同的數據集,也可以是側重于不同角度的特征提取方法,所以,這些視圖具有多種特征:有的是視覺底層特征、有的是視覺美學特征,甚至有中層語義特征.這些特征往往可以互補地描述圖像[4],因此,多視圖學習相比較于單視圖的方法能更有效地利用視圖之間的互補信息.而在實例檢索[5]任務上,Multi的思想[6]也被用于獲得更加精確的檢索效果.目前,利用多視圖來進行聚類分析的方法主要有兩種:多視圖譜聚類和多視圖K均值聚類.其中,多視圖譜聚類有文獻[7?11]等.雖然這些方法性能的相比單視圖的譜聚類有所提高,但是多視圖譜聚類需要為每一個視圖都計算親和矩陣,視圖越多,計算的復雜度也更大.相比之下,多視圖K均值聚類不需要計算親和矩陣,只需要利用原始特征即可.多視圖K均值聚類又分為基于指示矩陣的方法和基于NMF矩陣分解的方法.基于指示矩陣的方法有RMKMC[12]和DEKM(Discriminatively emmbedded K-means)[13]等,這種方法是從樣本角度來形成聚類質心,且這種方法的準確率依賴于指示矩陣的初始值.而基于NMF矩陣分解的方法是從維數的角度來進行降維,從而形成聚類質心.具體地,關于矩陣分解多視圖學習方面的研究有很多:在文獻[14]中,Kumar等利用全局和局部2種視圖的特征,提高了單視圖NMF在人臉識別問題上的準確率;文獻[15]利用稀疏編碼框架來對多視圖特征學習進行研究;文獻[16]中,Akata等提出Collective-NMF算法令多種特征數據共享相同的系數矩陣,這等同于先串聯各種特征然后進行NMF分解.然而Liu等認為這種共享系數矩陣具有太強的約束,提出一種弱化的約束,旨在保證每種特征的一致性,即視角間的一致性保持[17].

但是,以上這些方法沒有考慮相同樣本在不同視角中的空間結構關系,這種局部空間結構在半監督學習、流形學習等多個領域的方法中具有重要的意義.典型的計算空間局部結構約束的方法有 Locality preserving projection(LPP)[18]和Spectral Regression[19]等.Cai等在文獻[19]的算法中,通過引入局部結構約束達到了大幅度提高實驗準確率的效果.

因此,本文提出了一種基于局部結構約束的多視圖特征學習方法,稱之為MultiGNMF.這種方法的主要目標是相似的數據在每個視圖都有相近的相似性.因此,我們通過構建親和矩陣來將每個視圖的空間結構加入到目標函數中,并提出迭代規則來解決這個優化問題.然而,MultiGNMF等多視圖學習方法要求特征矩陣的值是非負的,而實際中并不能總是保證這一限制條件.為了消除這一限制條件,本文又提出了一種基于多視圖學習的MultiGSemiNMF算法.

文章主要結構分為4個部分:在第1節,簡要回顧一下基于矩陣分解的特征學習方法,并將局部結構約束引入多視圖學習框架中,提出基于局部結構約束的多視圖NMF分解算法—MultiGNMF;在第2節,針對MultiGNMF等多視圖學習方法只適用于非負矩陣的缺點,提出MultiGSemiNMF算法,并對其進行詳細介紹;第3節對所提的算法進行實驗驗證和分析;最后,第4節對本文的工作進行總結.

1 基于非負矩陣分解的特征學習方法及其存在問題

在這一節,我們首先介紹基于NMF分解的單視圖特征學習方法.然后,考慮到多視圖特征比單視圖特征能更好地描述圖像,且分解后的系數矩陣應與原始特征據的空間結構相似,我們提出了基于局部結構約束的多視圖特征學習方法—MultiGNMF.下面將分別介紹NMF和MultiGNMF這兩種特征學習算法.

1.1 NMF特征學習方法

下面介紹NMF的求解過程.

定義X=[X.,1,···,X.,N]∈RM×N為輸入數據矩陣,每一列都描述的是一個數據,U∈RM×K為基矩陣,V∈RN×K為系數矩陣,即新的描述子,兩者的乘積是對原始矩陣的逼近,如式(1)所示,其中K是一個變量,它決定了特征最終學習的特征維數.

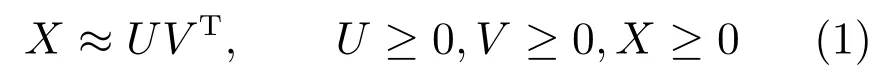
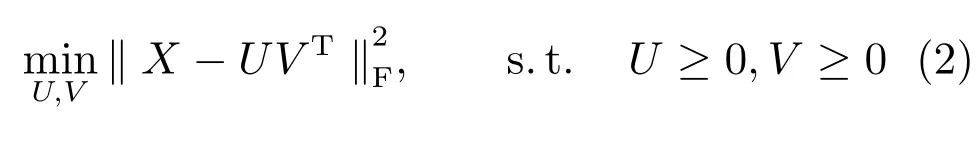
采用KKT(Karush-Kuhn-Tucher)條件,分別引入拉格朗日因子Ψ和Φ將U≥0,V≥0這兩個約束條件變成無約束優化問題,如式(3)所示.

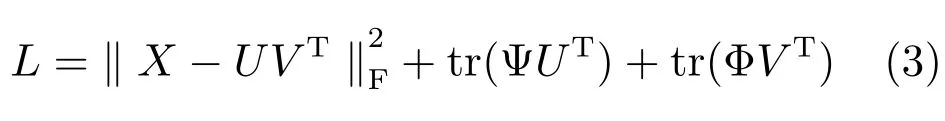
對于同時滿足U和V的條件下對于式(3)這種無約束優化問題是非凸優化問題,沒有精確的求解方法.文獻[19]提出了乘子更新法則來迭代求解上述最小化約束問題.迭代過程如式(4)和(5)所示.

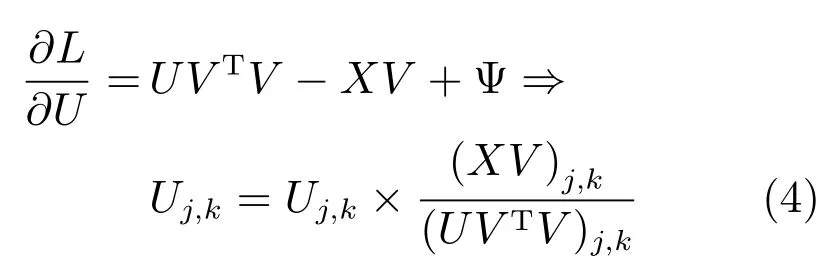
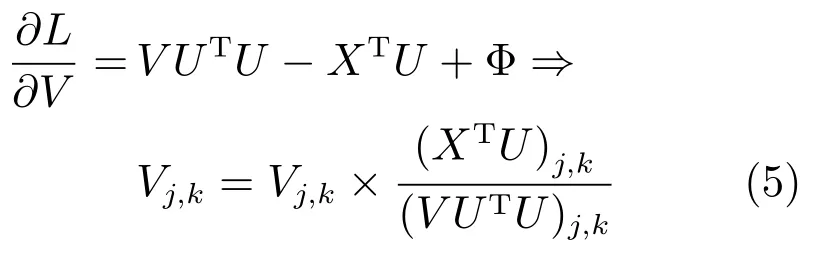
1.2 MultiNMF特征學習方法

NMF是基于單視圖的特征學習方法,然而,對同一個樣本而言,不同視圖的多種特征往往可以互補地描述圖像.基于此,文獻[17]提出了對每種特征保持弱化的一致性約束的多視圖學習方法—MultiNMF.現將MultiNMF介紹如下.定義X為G個視圖的輸入特征數據矩陣,為第f個視圖的特征矩陣.其中,Mf為第f個視圖的特征維數,N為樣本數據的數量.對應地,定義基矩陣U=U1,···,UG和系數矩陣V=V1,···,VG,Uf∈RMf×K,Vf∈RN×K.其中,K為定義的新特征維數.Liu在文獻[17]中提出Soft-regularization的方法認為,對每個視圖映射后的特征Vf需要保持一致性的約束,但是允許存在差異性,差異的大小采用歐氏空間中的lF范數來度量.于是,可以得到Liu的方法定義的損失函數如下式(6)所示.

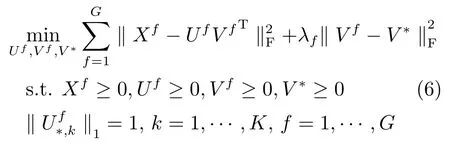
方程的解需要采用乘子更新法則來進行迭代求得,具體過程這里不再贅述.

1.3 MultiGNMF特征學習方法

局部空間結構約束的思想主要是保持樣本的局部空間結構不變(近似不變),這種局部空間結構在多個領域的方法中具有重要的意義.而MultiNMF沒有考慮相同樣本的原始數據與降維之后數據的空間結構關系,因此,本文提出了基于NMF矩陣分解的局部結構正則化約束多視圖學習方法,稱之為MultiGNMF.下面對MultiGNMF方法進行詳細介紹.

1.3.1 局部結構正則化約束

局部空間結構近似不變的具體含義就是:如果兩個樣本xi和xj在原始空間中相似,那么我們認為它們在映射后的空間中(分別用Vi,.和Vj,.表示)也應該有近似的相似程度,即原始數據與映射后的數據有相似的局部結構關系.

根據以往文獻的考察,我們采用數據的親和矩陣W來表征局部結構關系.計算親和矩陣的方法很多,在沒有監督信息的前提下,一般采用數據之間的歐氏距離構建親和矩陣W.定義一個正整數變量k,一個樣本i與其他樣本的權重可以如此計算:對所有樣本與該樣本的距離進行從小到大的排序,如果樣本j在前k個,那么Wij=1;否則,Wij=0.還有其他的方法不采用0/1值作為權值,而是直接用數據之間的核函數值作為權值.典型的核函數有高斯核,線性核等.不同的計算方法適應于不同的研究內容,在文檔特征中采用線性核表現更好,在圖像視覺特征中高斯核可能更適合.在和其他的方法比較的過程中,我們采用比較通用的高斯核函數值作為權值,從而就可以得到原始數據的親和矩陣W.但是,這些方法的性能受參數的影響較大.最近,Nie等[20]提出了一種無參數構建親和矩陣W的方法,該方法不需要任何參數,很好地解決了構圖過程需要反復調節參數的問題.但本文提出的MultiGSemiNMF和MultiGNMF算法直接應用無參數構圖后缺乏普適性,因此本文仍然使用高斯核函數來構建親和矩陣,在以后的工作將深入研究無參數構圖和本文方法的結合.對于經過映射后的數據Vi,.和Vj,,,仍用歐氏距離來度量它們之間的相似程度,如式(7)所示.利用親和矩陣W,我們便可以構造用于約束局部結構的平滑懲罰因子.對于第f個視圖的平滑懲罰因子Rf,公式如下:

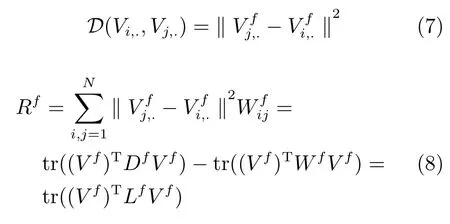
其中,L=D?W為拉普拉斯矩陣,D是一個對角矩陣.

1.3.2 目標方程的構建及求解

將平滑懲罰因子引入多視圖特征學習Multi-NMF的框架中,我們得到MultiGNMF方法的目標函數如下:

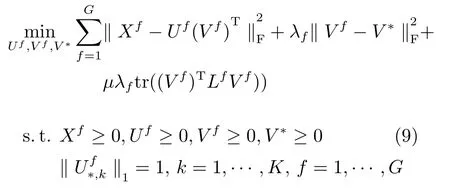
Liu在文獻[17]中建議用對角陣Q歸一化U和V,即UVT=UQ?1QVT.其中,Qf定義如下:

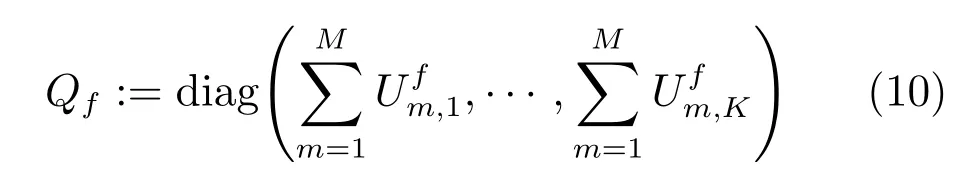
diag(·)表示對角矩陣.這樣,經過歸一化后,.因此,式(9)可以改寫成:

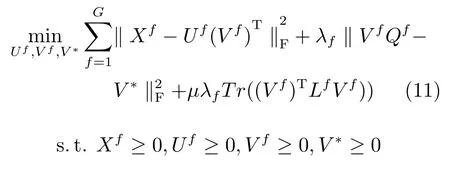
由此,我們可以得到整體的損失函數定義如式(12)所示.

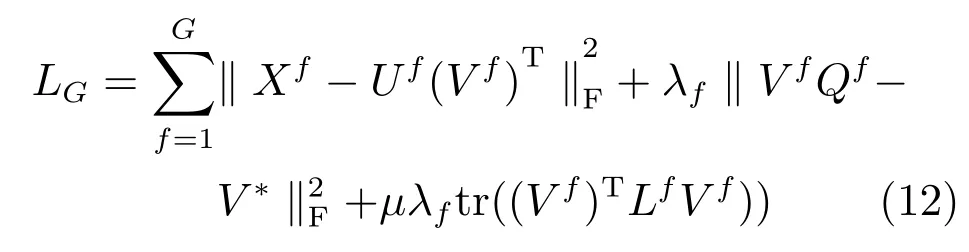
MultiGNMF在Uf≥0,Vf≥0的約束下最小化LG是一個帶約束的優化問題.采用迭代的方法求解.引入拉格朗如因子后,MultiGNMF的第f種特征損失函數為式(13).

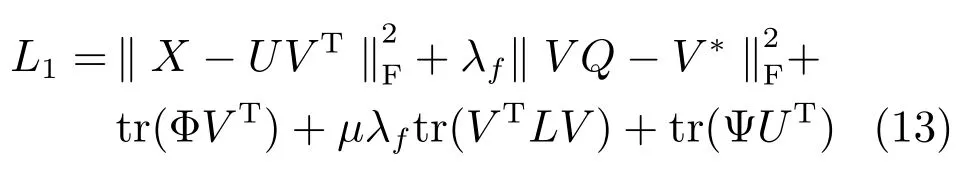
L1分別對U和V求導,求導結果如下:

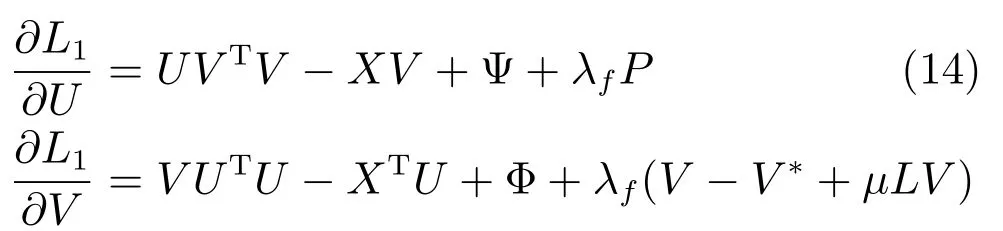
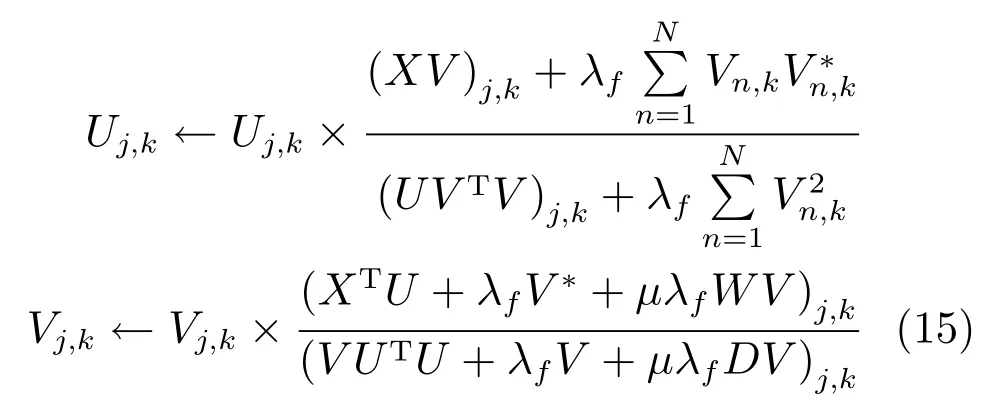
根據文獻[17],我們在每次迭代得到U和V之后,按照式(10)進行歸一化處理,即:

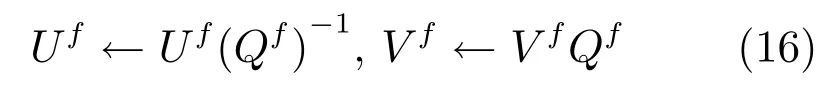
在優化U和V之后,將它們視為常量,對L1求導得到V?的更新表達式如下所示:

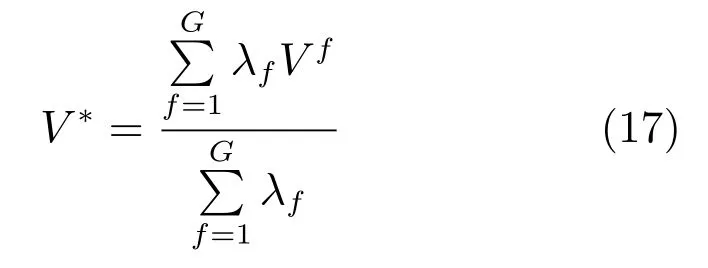
NMF和MultiGNMF都要求U≥0,V≥0,X≥0.這種非負性約束來源于在現實世界中大部分數據是非負的,系數的累加也是非負的.然而,實際情況中,我們提取到的圖像特征往往存在負數,這就使得以上兩種特征學習方法存在局限性.為了消除這個局限,我們提出一種對負數特征也適用的多視圖特征學習方法—ultiGSemiNMF,我們將在下一節對其進行詳細介紹.

2 MultiGSemiNMF特征學習方法

在第1節中我們分析了各種基于NMF矩陣分解的特征學習方法的優越表現,不過這些方法有一個重要的約束:所有數據都必須是非負的.在物理世界中可能大部分數據保持這個特性,但是,在圖像處理中有些特征,如由小波變換得到的三分法特征、結構特征等,并沒有保持非負性的條件,如果強制向正數方向映射,往往含有一定的失真.這就使得基于NMF的特征學習方法有一定的局限性.如何將NMF算法拓展到對負數矩陣也適用,文獻[13]中進行了詳細探究.其中一種方法是SemiNMF,下面我們對其進行介紹,并由此引出本文所提算法—ultiGSemiNMF.

2.1 SemiNMF特征學習方法

SemiNMF中的數據與NMF中的數據一致,但是,SemiNMF算法對原始數據X和基矩陣U不帶有非負性約束,只需系數矩陣V≥0.由此,我們可以得到SemiNMF的目標方程和損失函數分別如式(18)和(19)所示:

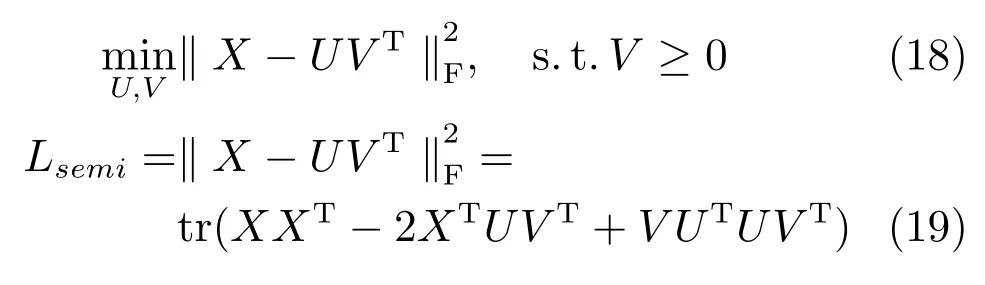
SemiNMF在V≥0的約束下最小化Lsemi是一個帶約束的優化問題.采用迭代的方法求解,求解過程我們將在第2.2節具體介紹.

2.2 MultiGSemiNMF特征學習方法

SemiNMF這種方法具有很好的描述性,同時相對NMF有較大使用范圍和較高性能.于是,為了克服基于NMF的各種特征學習方法只適用于非負數據的缺點,本文提出基于SemiNMF的多視圖特征學習算法,我們稱之為MultiGSemiNMF.下面將對這種方法做詳細的介紹.

2.2.1 目標方程

多視圖學習過程中我們需要遵守幾個準則:1)每個視圖學習的新特征需要保持一致性;2)在學習前的特征和學習后的特征對樣本之間的局部結構進行度量,需要保持這種結構的一致性.于是,我們得到弱化的一致性約束項和局部結構正則化約束項tr((Vf)TLfVf).我們將多視圖學習的準則應用到SemiNMF,于是,我們可以得到MultiGSemiNMF算法的目標函數如式(20)所示.

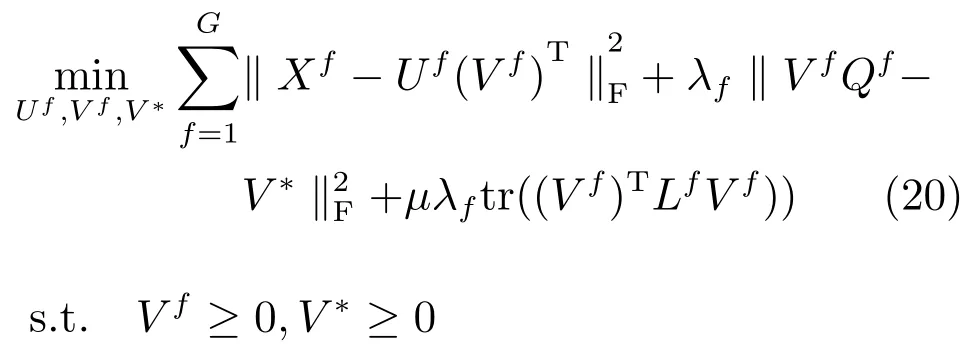
其中,Qf的引進是為了使方程滿足的約束條件.而的約束條件是為了每一種特征的數據歸一化處理,那么對應的系數矩陣也變得歸一化,具有比較性.又因為.所以,在U歸一化之后如果對X也進行歸一化處理,V便也達到歸一化的目的.而X為原始數據我們能更好的操作,故在求解過程中只需要在每次迭代U之后對其進行歸一化即可.所以,式(20)可以簡寫成(21),但是我們需要求解前對原始數據X進行歸一化操作,在每次迭代后對U進行歸一化.

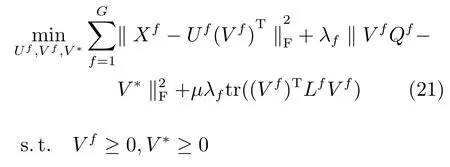
由此,我們可以得到MultiGSemiNMF算法的整體損失函數如下所示:

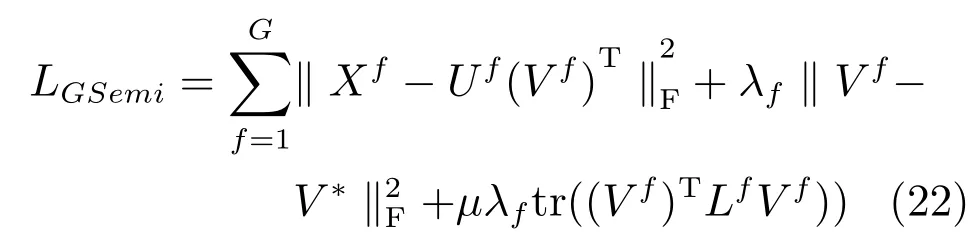
其中,L=D?W為拉普拉斯矩陣,D是一個對角矩陣,W為樣本在原始空間關系的親和矩陣.各變量的具體含義及計算方法詳見第1.3節.

2.2.2 方程求解

MultiGSemiNMF在Vf≥0的約束下最小化LGSemi是一個帶約束的優化問題.對于每個視圖的特征,引入拉格朗日因子后,MultiGSemiNMF的第f個視圖特征的損失函數為

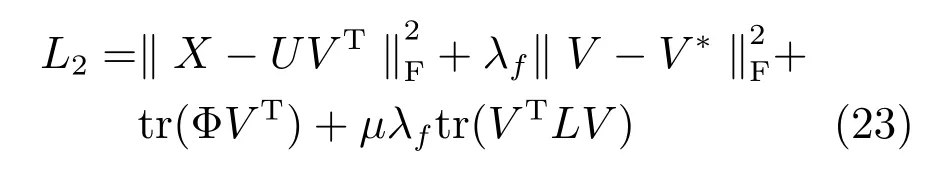
損失函數在變量U和V下不是一個凸優化問題沒有精確的數值解,采用迭代優化方法求解,具體計算步驟如下:

1)對V取隨機矩陣或者采用K-means算法得到的系數矩陣.

2)固定V更新U.將L2中只有變量U,變成一個無約束優化問題,對其求導,獲得U的解析解.其中VTV∈RK×K在一般情況下是一個半正定的矩陣,在不可逆的情況下,用偽逆矩陣來代替(Matlab中的pinv函數).

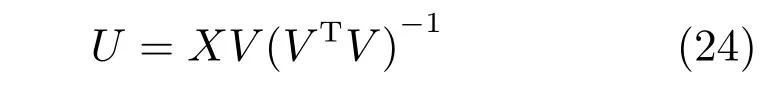
3)固定U更新V.將U固定,L2中只有變量V,對其求導=0,采用KKT條件Φj,kVj,k=0獲得式(25)的優化問題.

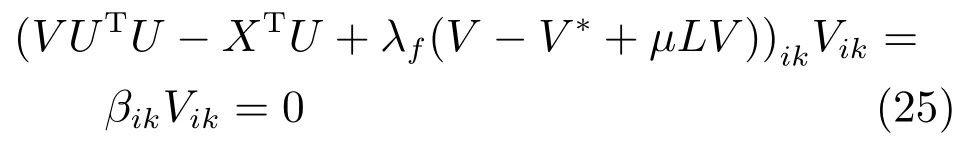
式(25)是一個典型的定點等式問題,求解f(x)=0,可以變成x=g(x)的形式,迭代式子xi+1=g(xi)由于存在V≥0的約束條件,式(25)中的各項需要保持絕對的非負性.所以,我們采用拆分的方法.通過拆分,XTU=(XTU)+?(XTU)?,UTU=(UTU)+?(UTU)?,其中的拆分函數定義如式(26)所示.這樣式(25)便變成多個非負矩陣之間的線性組合.

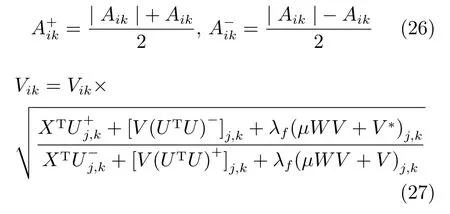
文獻[21]提出一種滿足定點等式的x=g(x)形式,將式 (27)所示,代入到式 (25)中(V UTU?XTU+λf(V?V?+μLV))ikVik0,由于KKT條件約束βikVik=0,當Vik6=0時,必然存在(V UTU?XTU+λf(V?V?+μLV))ik=0,式(27)滿足式(25);反之,當Vik=0也滿足.綜合考慮,式(27)滿足KKT條件.迭代式(27)的收斂性證明方法可以詳見文獻[21?22].

4)交替迭代第2)步和第3)步,直到損失函數值小于閾值或損失函數值變化小于閾值.

5)在優化U和V之后,將它們視為常量,利用式(17)更新V?.MultiGSemiNMF與Multi-GNMF的不同之處在于缺少了Uf≥0的約束,因此不僅適用于特征矩陣非負的情況,在特征矩陣中存在負數時,也表現良好.式(28)是各種變量的迭代方程.

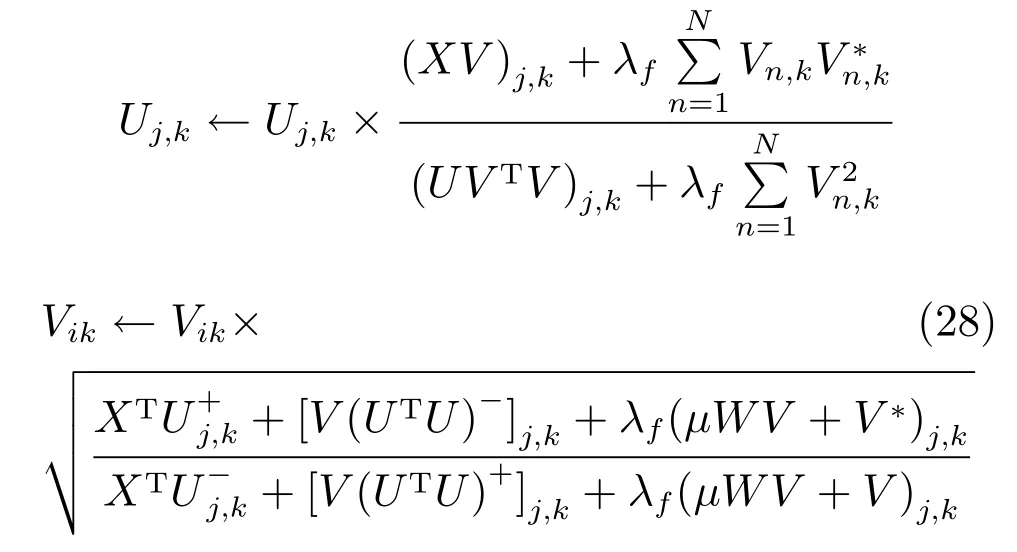
3 實驗設計與分析

為了驗證MultiGNMF算法和MultiGSemiNMF算法的有效性,我們在4個公共的圖像數據庫中和其他幾種多特征學習算法比較圖像聚類效果.下面分別從實驗設置、評估指標和實驗結果及分析這三部分作詳細介紹.

3.1 實驗設置

3.1.1 數據庫

實驗中所用的數據庫為CMU PIE人臉數據庫、UCI手寫體數字圖像數據庫、3-Sources文本數據庫和ORL人臉庫.表1詳細介紹這4個數據庫的統計特性.具體介紹如下:

CMU PIE人臉數據庫包含41368張32×32像素的人臉圖像,這些數據是68個人按照指定的13種姿勢角度和43種不同光照條件下采集人臉的圖像.在實驗中,我們從每個人的一個角度中隨機選擇42幅圖像,構成2856幅人臉圖像.如果按照人臉作為聚類中心的話,那么數據可以分成68個集群.在本次實驗中,我們用圖像的像素值(二維圖像按行展開)和HOG(Histogram of oriented gradient)特征作為CMU PIE的兩個視圖.

UCI手寫體數字數據庫有UCI大學構建數字0～9的手寫體圖像,數據庫包含2000個樣本.我們利用手寫體圖像的低頻傅里葉變換和原始像素值作為不同的視圖.

3-Sources文本數據庫包含BBC、Reuters和Guardian三種流行的網上新聞資源.其中,有169條新聞被這三個新聞網報道過.我們選取這169條新聞作為測試樣本,這三個新聞網分別作為三個視圖來進行聚類分析.這些新聞的主題包含商業、娛樂、健康、政治、運動和科技,我們將其作為我們聚類的標簽.

ORL(Olivetti research laboratory)人臉庫是英國劍橋大學Olivetti研究所制作的人臉數據庫,它共包含400張的人臉圖像.這些數據是40個人在不同的時間、變化的光線、面部表情(張開/合攏眼睛、微笑/不微笑)和面部細節(戴眼鏡/不戴眼鏡)下拍攝的.所有的圖像為實驗者的正臉,帶有一定程度的朝上下左右的偏轉或傾斜,相似的黑暗同質背景.所有圖像的大小均為28×23像素.在本次實驗中,我們用圖像的像素值(二維圖像按行展開)和低頻傅里葉變換系數值作為ORL的兩個視圖.

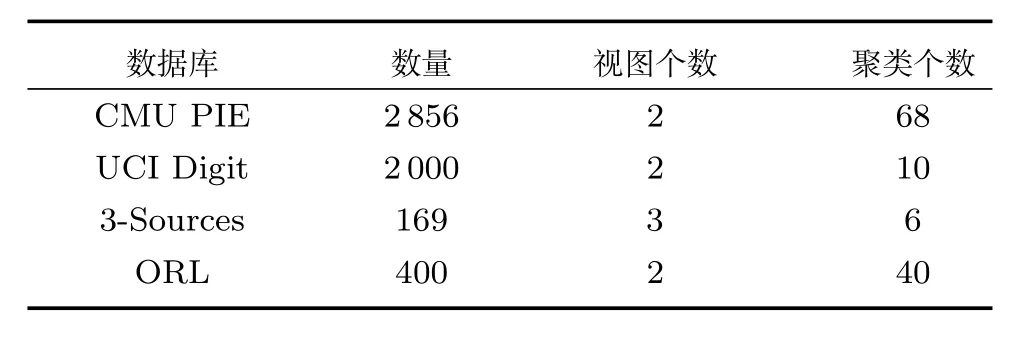
表1 4個數據庫的資料Table 1 The information of four databases

3.1.2 對比算法

為了更全面地評估本文提出的算法,我們比較了近期多種典型的多視圖學習算法.下面對它們進行描述.

1)單視圖算法(BSV和WSV):我們對每個視圖利用NMF算法進行特征學習,將學習的系數矩陣作為特征.統計每個視圖的效果,我們取每個視圖該算法對應的最好效果為BSV和最差效果為WSV.

2)ConcatNMF:這是一種前向融合的學習方法.其算法可以簡單理解為,首先將每個視圖的特征串聯成一個向量(矩陣)作為數據新的特征,然后利用非負矩陣分解算法進行特征學習,所有算法流程和度量標準與單視圖的方法一致.

3)ColNMF:一種多視圖學習方法,采用一致性準則,如式(29)所示,所有的視圖共享相同的系數矩陣.與ConcatNMF類似,不過每個視圖添加了權重和歸一化約束.min

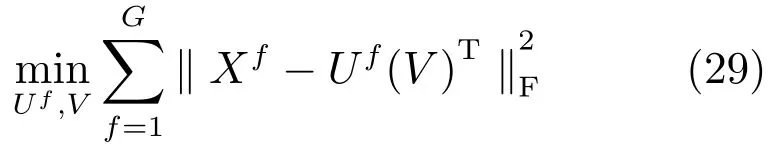
4)Co-reguSC:一種改進的譜聚類算法,在文獻[23]中被Kumar等提出.每個視圖采用譜聚類學習作為基本的聚類學習算法,與MultiNMF算法相似的是,在視圖之間采用弱一致性準則約束各個視圖的映射矩陣之間的關系,如式(30)所示.在實驗中我們采用高斯核核函數,該算法的詳細介紹可以參考文獻[23].

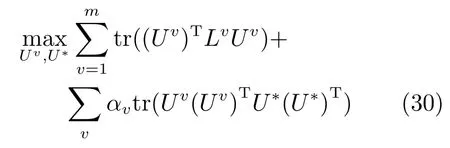
5)MultiNMF:本文算法的基準算法,采用弱一致性約束的多視圖NMF學習方法.

6)Sc-ML:是一種改進的Co-reguSC算法.Dong等在文獻[24]中提出,利用格拉斯曼流行距離中的一種投影距離來定義不同視圖學習的子空間之間一致性準則.

7)MMSC:是一種多模態的譜聚類方法.不同的模態(也就是圖像特征)共享一個相同的圖拉普拉斯矩陣,也就是最后的聚類指示矩陣G.該算法的詳細介紹可以參考文獻[10].

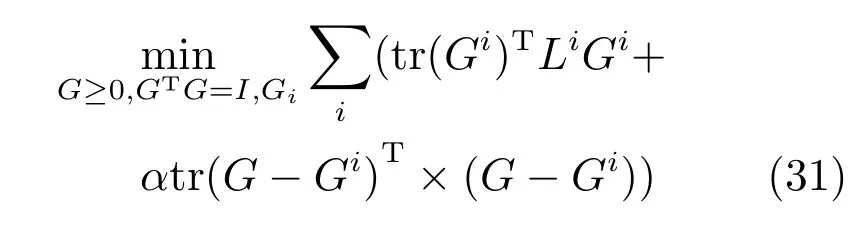
8)AMGL:是一種多視圖譜聚類方法.但是不同視圖所占的權重是自動學得的,不需要有額外的參數來指導訓練.該算法的詳細介紹可以參考文獻[11].

3.2 評估指標

本文采用以往文獻中的經典評估方法:AC(精確度)和NMI(歸一化互信息)來度量圖像數據聚類的評估指標.給定一幅圖像,定義為圖像的標簽類別,為圖像對應的聚類中心的類別標簽,AC可以用如下式(31)來定義.其中n為所有的測試圖像數量,是一個脈沖函數,函數中兩個參數相同則返回1,否則返回0.是一種將聚類中心的標簽映射到圖像集已知的對等標簽,其中我們采用Kuhn-Munkres[25]的映射方法.

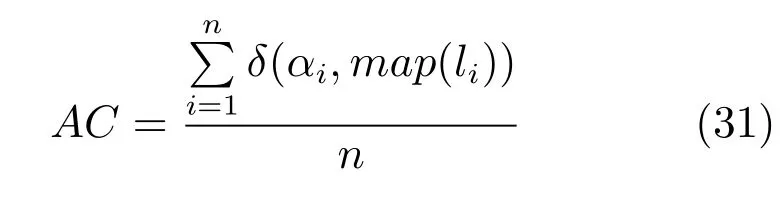
給定兩個數據集的所有聚類中心,它們之間的互信息可以用式(32)計算.

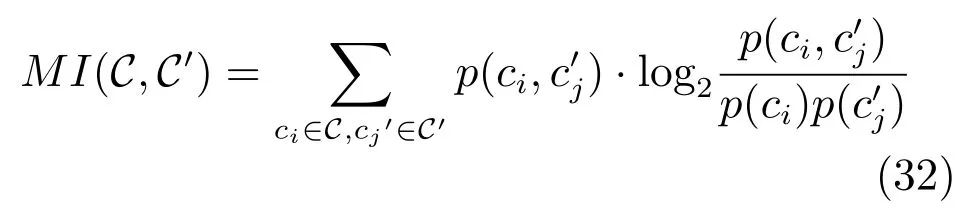
其中,p(ci)和表示在所有測試圖像中被分到各自對應聚類中心的概率,在這里我們用數量比率代表概率,表示一個圖像被同時分到這兩個聚類中心ci和的概率,同樣我們用數量比代替概率(注意在這里聚類算法計算得到的聚類中心的編號可以為任意的順序).在實驗中,第一個聚類中心集為圖像的已知類別標簽,同一個標簽的圖像為一個聚類中心,第二個聚類中心集為聚類算法得到的標簽,標簽可以為任意的順序標簽.歸一化的互信息為互信息除以最大的聚類標簽熵,其中H(C)=?Pip(ci)log2p(ci),p(ci)指屬于聚類中心ci的圖像數量比率.

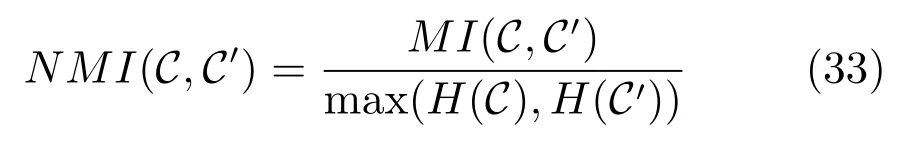
3.3 實驗結果與分析

3.3.1 聚類的準確性驗證

在本文提出的方法需要計算各個數據之間的局部結構關系,我們采用高斯核函數值作為權值,即.變量k=5,這種參數設置在非大量樣本數據庫中使用的較多.在式(12)中所有的變量我們設定為λf=0.01(f=1,···,G),μ=10,與算法MultiNMF和MultiGNMF保持一致.

在定義了參數之后,計算每個視圖圖像之間的親和矩陣,每種方法我們都運行20次,取所有次數運行結果的平均值和方差作為最終的算法效果評估值.經過20次的實驗運行,我們統計了各種算法在4個數據庫上的AC和NMI值,如表2和表3所示.

在表2和表3中我們可以看到本文提出的算法在聚類分析中相比較其他多視圖學習算法在準確度和歸一化互信息兩個指標下都有較好的表現.同時我們注意到Co-reguSC和SC-ML算法也采用了局部結構約束的條件(譜聚類算法是一種基于數據樣本圖結構的算法),MMSC也采用了一致性約束,本文算法同樣超過該類算法.在比較本文提出的算法MultiGSemiNMF和MultiGNMF算法中,我們發現基于MultiGSemiNMF的算法相對于MultiGNMF算法聚類效果上也有提升,即使所有特征并沒有負數或零,這證明在特征學習中MultiGSemiNMF算法比MultiGNMF算法在一些應用場景中具有更好的表現,且MultiGSemiNMF消除了MultiGNMF算法要求所有特征非負的限制,因此也有著更為廣闊的應用平臺.

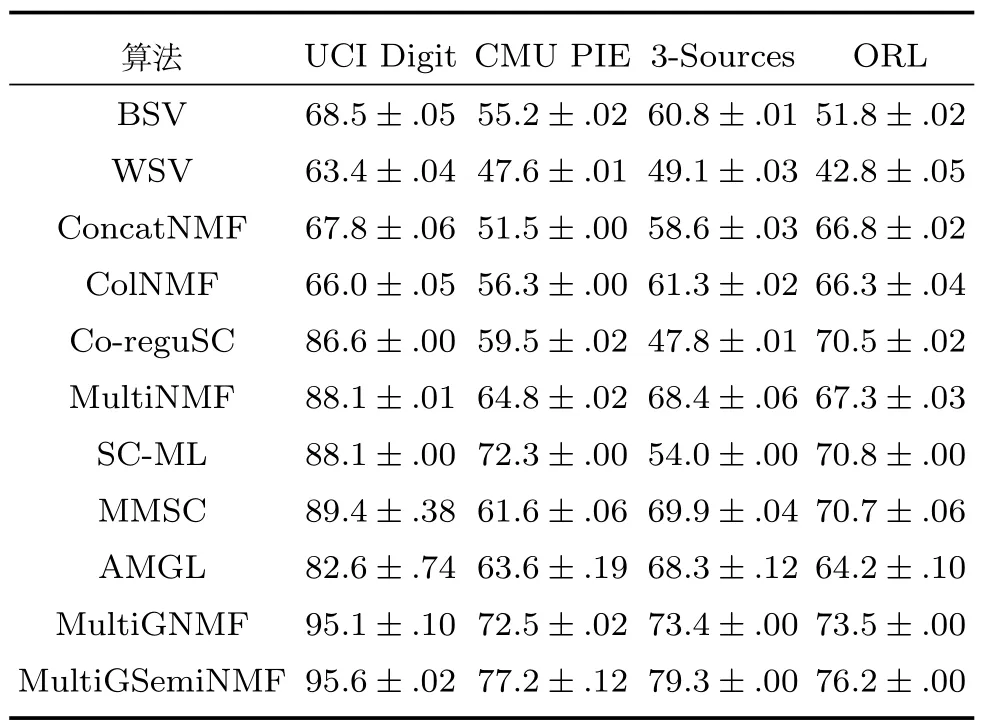
表2 不同方法在4個數據庫中的AC值Table 2 The AC values by different methods in four databases

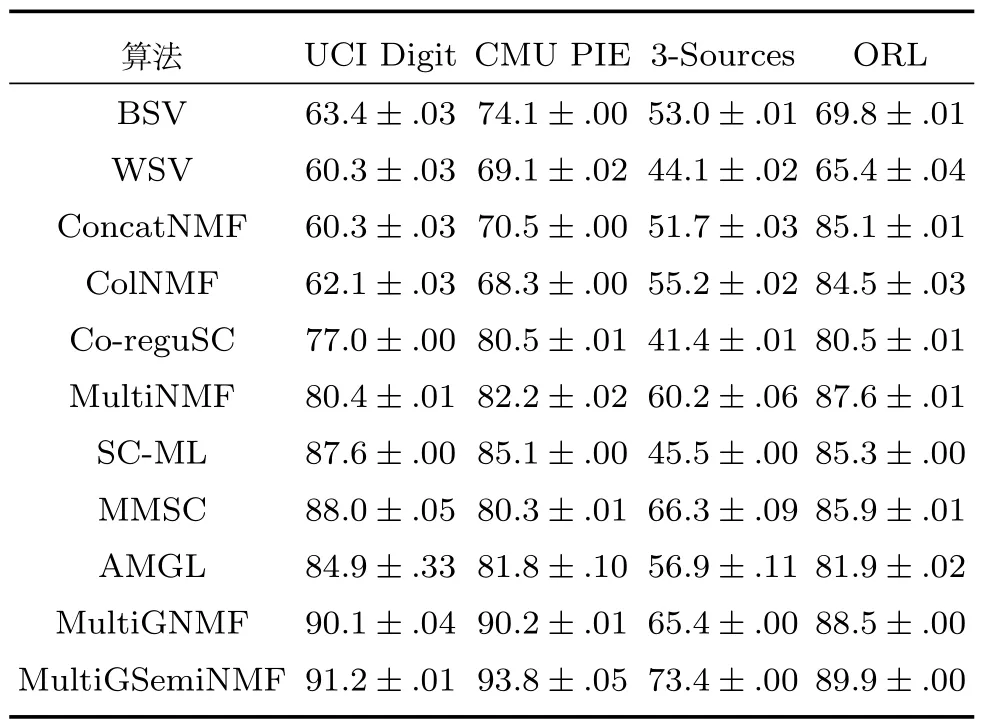
表3 不同方法在4個數據庫中的NMI值Table 3 The NMI values by different methods in four databases

3.3.2 參數對算法性能的影響

在式(12)中有G個參數變量λf,它的物理意義是不同視圖對學習過程的重要性進行權衡.如果我們具有一些先驗知識,帶有噪聲的視圖特征可以適當減少權重,被認為重要的視圖如文本標簽信息等可以適當增加權重.在我們的實驗中沒有先驗知識,同時數據已經歸一化處理,所以所有的λf定義為相同的數.但是λf的大小會影響聚類效果,λf越小則對系數矩陣的一致性約束越松弛,反之,λf為無窮大的話所有系數矩陣為相同的數值.

下面我們在兩個數據庫CMU PIE和UCI Digit上用MultiNMF、MultiGNMF和MultiSemiNMF三個算法做聚類分析,準確率AC作為指標度量不同的λf值對實驗的影響.我們設定λf為0.001,0.005,0.002,0.01,0.02,0.05,0.1,圖1和圖2描述了對應的聚類效果.

從圖1和圖2中我們可以看到,在Multi-NMF、MultiGNMF和MultiSemiNMF三個算法中,MultiGSemiNMF算法的準確率最高,且受參數影響很小,在較小或者較大的值均能有穩定的表現.MultiGNMF算法最不穩定,但是在大部分實驗中仍能超過基準算法MultiNMF.三種算法均在λ=0.01時有較高的表現.

圖1 在UCI Digit數據庫中參數λ對本文算法的影響Fig.1 The in fluences ofλon UCI Digit database

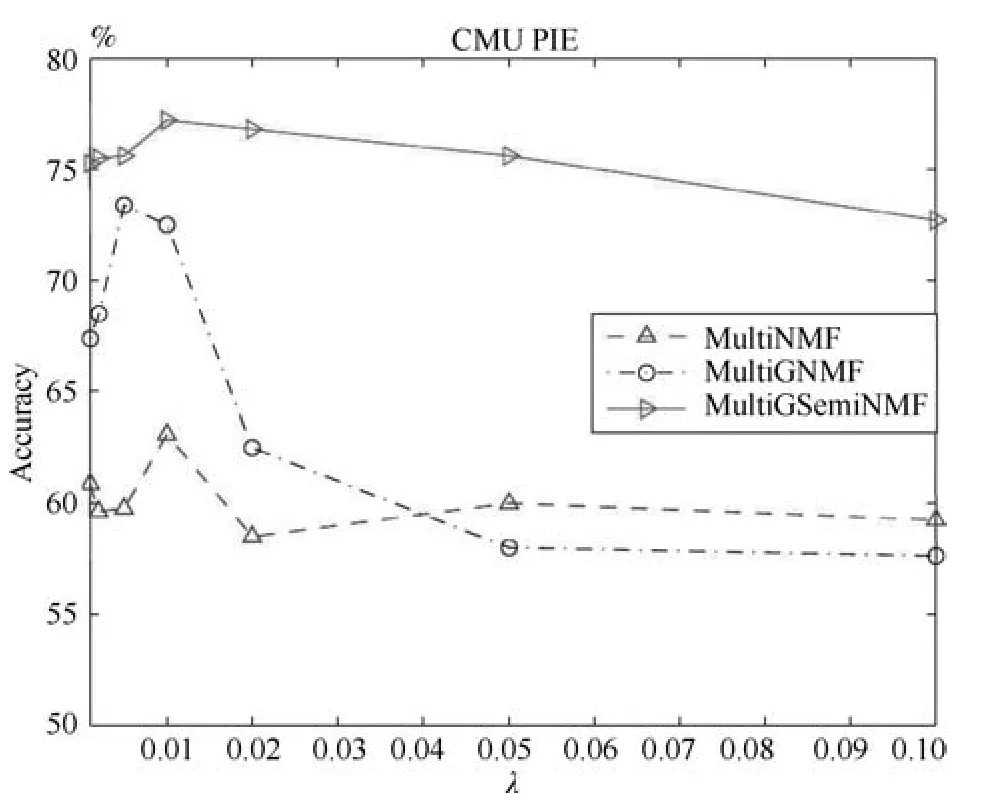
圖2 在CMU PIE數據庫中參數λ對本文算法的影響Fig.2 The in fluences ofλon CMU PIE database

本文提出的算法MultiGSemiNMF和Multi-GNMF需要構建一個樣本親和矩陣,在損失函數其中有一個參數k,k值越大樣本的局部結構約束越多,反之局部結構約束越少.不同的k值對聚類效果有一定影響,在與其他算法的比較中,我們采用其他算法一樣的k值,在這里我們另外分析k值對本文提出算法的影響.在UCI Digit數據總庫,我們選取k=5,10,15,20構建親和矩陣(λ=0.01),用聚類的準確率AC來評估算法效果,如圖3所示.

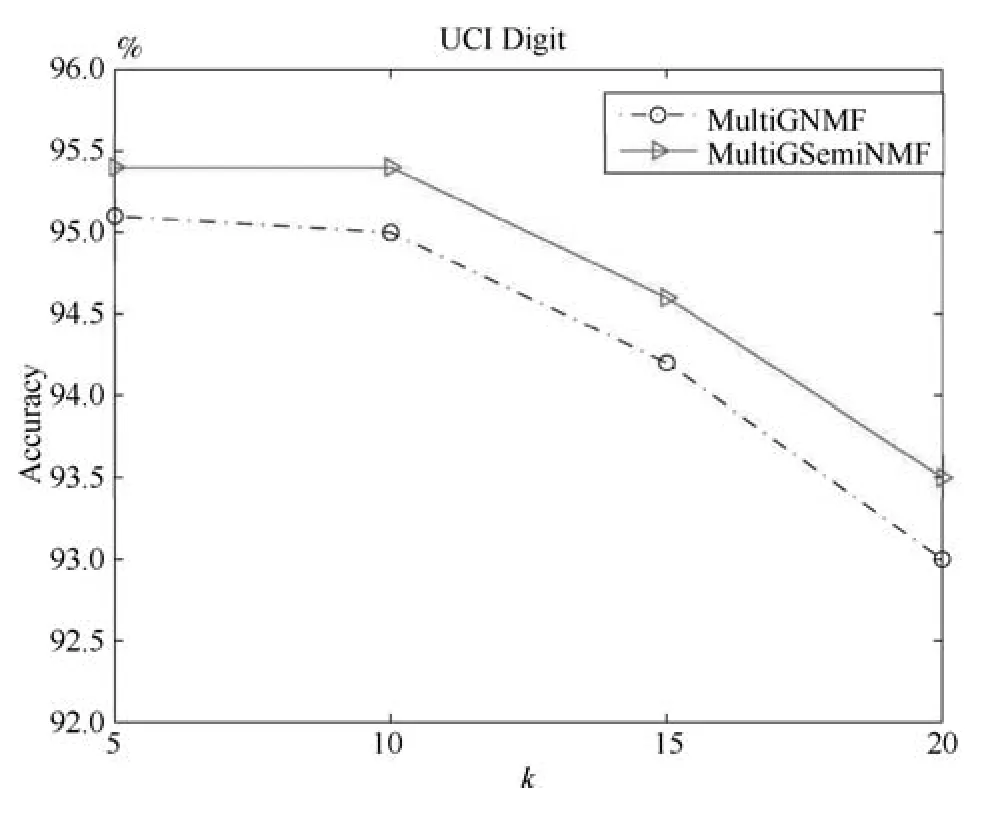
圖3 在UCI Digit中參數k對本文提出算法的影響Fig.3 The in fluences ofkon UCI Digit database

從圖3我們看到參數k對本文算法有一定的影響,k值越大雖然能更充分地保留樣本之間的局部空間結構關系,但是從圖中的結果來看聚類準確度隨著k的變大有降低的趨勢.過度的保留空間結構關系并不能提升算法的效果,反而可能產生過度擬合的副作用,因為樣本的結構關系是基于原始特征的距離計算得到,而原始特征并不能充分描述樣本信息,其中或多或少含有冗余和噪聲.同時,也可以看出,無論參數k取何值時,MultiGSemiNMF算法的性能都優于MultiGNMF算法.

4 總結

本文提出了兩種多視圖學習的方法:Multi-GNMF算法和MultiGSemiNMF算法.Multi-GNMF和MultiGSemiNMF算法都是基于樣本局部結構空間約束的非負矩陣分解多視圖學習方法.

本文首先介紹了一種單視圖學習方法:NMF矩陣分解.然后,NMF算法的基礎之上,在以往多視圖學習的框架準則下,本文提出了基于樣本局部結構空間約束的非負矩陣分解多視圖學習方法MultiGNMF.但是,MultiGNMF方法只適用于非負的特征矩陣.MultiGSemiNMF算法則不限于此.

為了驗證本文提出的多視圖學習算法的性能,我們在公有的圖像數據庫中做聚類分析.實驗中和以往的算法比較,實驗結果表明本文提出的算法相對于其他基于矩陣分解的多視圖學習方法有更好的表現.同時實驗中分析了算法中的參數變化對算法性能的影響,實驗結果表明MultiGSemiNMF對參數變化具有很好的魯棒性.在未來的工作中,我們將探索一種新的基于局部結構約束的多視圖學習方法.