基于GA-BP神經網絡的胎兒體重預測分析①

朱海龍, 陶 晶, 俞 凱, 朱旭紅, 袁貞明

1(杭州師范大學 杭州國際服務工程學院,杭州 311121)2(南京醫科大學,南京 211166)

3(杭州市衛生和計劃生育委員會,杭州 310006)

4(杭州市婦幼保健院,杭州 310008)

1 引言

在婦產科學中,準確預測胎兒體重具有十分重要的意義. 胎兒體重是判斷胎兒發育的重要指標之一,孕中期計算胎兒體重,可以監測胎兒發育是否正常,且孕晚期計算胎兒體重對產婦的生產方式有指導作用. 隨著經濟水平的提高和醫療條件的改善,巨大兒的發生率也在逐年上升,占新生兒的5.62%-6.49%[1]. 由于孕婦營養過程引起巨大兒的發生比率接近70%,隨之而來的問題就是難產、剖宮產比率增加[2]. 然而,胎兒體重無法直接測得,只能根據孕婦體檢數據進行預測.

傳統的胎兒體重預測是基于孕婦體檢時的B超檢查結果來預測胎兒體重預測模型. Shepard等[3]使用雙頂徑 (BPD),腹圍 (AC)等參數直接計算胎兒體重;Hadlock等[4]使用頭圍 (HC),腹圍 (AC),股骨長度(FL)等參數,通過回歸分析得到的經驗公式預測胎兒體重. 朱桐梅等[5]比較了6種利用宮高、腹圍數值的胎兒體重經驗公式的準確性,其中最高的精確度為45.76%,難以滿足當前的醫療需求. M?st L等[6]認為傳統經驗公式是基于單次點預測的結果,易于解釋其意義,但是忽略了對預測區間不確定性的度量,因此提出基于條件線性變換模型預測胎兒體重,將不同預測區間的不確定性度量引入預測模型,提升模型適應度. 洪傳美等[7]指出目前臨床工作中使用的經驗公式多為國外學者創立,由于不同人種之間的種族差異,使得測量結果也存在較大差異,因此,經驗公式預測方法在使用過程中需要根據具體情況作出適當調整. 由于孕產婦所在地區的不同、孕產婦本身參數的差異以及測量方法的差異,很難建立一個通用的經驗公式,因此經驗公式預測的準確率較低[8]. Farmer等[9]首次提出利用人工神經網絡進行胎兒體重預測,在B超檢查結果基礎上增加了孕婦本身的生理特征,基于BPD,HC,AC,FL,羊水指數(AFL),孕婦年齡,孕次,產次,身高等參數,使用BP人工神經網絡預測胎兒體重. 結果顯示使用BP人工神經網絡預測結果優于傳統回歸分析結果. 隨后Cheng等[10]提出基于聚類的人工神經網絡模型進行胎兒體重預測. Mohammadi等[11]利用人工神經網絡預測雙胞胎胎兒體重. 李昆等[12]基于深度神經網絡的胎兒體重預測模型,利用胎兒和孕婦產前檢查記錄作為模型特征輸入預測胎兒體重. 然而,以上預測模型均基于單次橫斷面時間的孕婦或胎兒檢查參數信息,預測準確率仍舊不高.

本文基于孕產婦從懷孕開始到結束的歷史體檢數據建立孕婦連續體征變化模型,使用遺傳算法優化的BP神經網絡(GA-BPNN)構建胎兒體重預測模型,在我國東部某醫院3000例臨床數據集上進行實驗. 結果表明,基于GA-BPNN的胎兒體重預測模型比傳統BP神經網絡的預測方法提升了14%的預測精度.

2 數據預處理

孕產婦產檢次數不同、產檢機構不同、每次檢查內容不同等都會導致孕產婦的歷史體檢數據的不完整,會干擾預測模型的訓練和預測過程. 因此,數據預處理過程是提高數據質量的關鍵步驟. 本文在預處理過程中首先對原始數據進行缺失值處理、特征標準化操作,形成孕婦連續體征變化模型.

2.1 預測模型輸入屬性參數

孕產婦的各項歷史檢查數據存在于電子病歷系統(EMR)以及檢驗檢查系統(LIS)中,本文從這些系統中以孕婦身份證為主索引提取從孕早期開始到分娩的各項檢驗檢查數據,以及出生胎兒的真實體重,形成體重預測的樣本集合. 定義Y為胎兒真實體重集合,定義X為模型的輸入參數集合,該集合由15個參數組成,X={xg,xp,xh,xw,xa,{weightt},xhc,xbpd,xac,xfl,xafi},其中{weightt}表示孕產婦在孕期不同時間的體重變化量,其余各參數意義如表1所示.

表1 預測模型輸入屬性參數列表

2.2 缺失值處理

基于歷史檢查數據的預測模型中存在的一個現實問題是,由于孕產婦的產檢時間、次數不固定,會導致體重序列值缺失,本文采用回歸法補全缺失的體重序列值. 基于孕產婦已有的體重數據集建立回歸方程,篩選出產檢記錄數大于5的孕婦,獲取孕婦孕期不同時間(以天為單位)的體重值,以此作為數據集,為每一名孕產婦建立回歸方程,回歸方程采用二次擬合函數.給定數據序列(xi,yi),其中xi為孕期天數,yi為xi時的體重. 設P(x)為二次擬合函數,得到擬合函數與實際體重序列的均方誤差：

通過求解式(1)的極小值獲得二次擬合函數參數.本研究中隨機抽取1000例樣本數據進行擬合函數實驗,得到擬合結果的平均相對誤差率為2.14%. 通過上述方式,獲取孕產婦體重序列集合{weightt},完成缺失值處理.

2.3 特征標準化

通過數據預處理與缺失值處理后,得到模型輸入參數集合,但由于不同生理參數具有不同的單位和數量級,為消除單位和數據量級不同對模型預測結果的影響,在參數輸入網絡模型前要進行數據歸一化處理,保證各個參數處在同一個數量級[13]. 標準化采用式(2)所示的計算方法,其中x表示當前特征值,xmin、xmax表示當前特征值得最小值、最大值.y為標準化后的特征值. 標準化后的數據范圍為[-1,1].

3 構建GA-BPNN胎兒體重預測模型

本文提出的胎兒體重預測模型采用遺傳算法優化的BP神經網絡,利用遺傳算法的優化全局優化搜索能力優化神經網絡的初始權值和閾值,從而解決BP神經網絡的局部收斂問題,即將神經網絡初始化權值和閾值作為初始種群進行編碼,利用遺傳算法優化得到最終的權值和閾值,在進行神經網絡學習.

3.1 GA-BPNN胎兒體重預測模型

胎兒體重預測模型是一個三層BP神經網絡,利用遺傳算法根據訓練目標函數優化BP神經網絡的初始權值和閾值,采用誤差逆傳播(Error Back-Propagation,BP)[14]算法學習神經網絡模型. BP神經網絡結構如圖1所示.

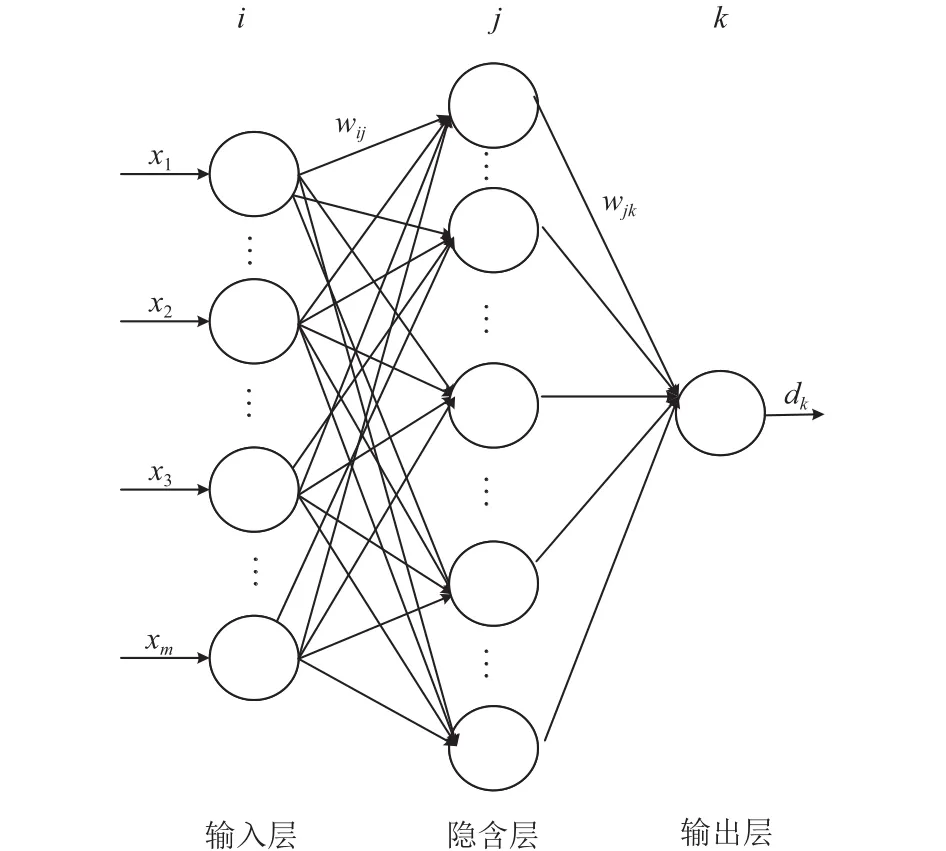
圖1 三層BP神經網絡結構圖

圖1中,輸入層包含15個神經元(生理參數),分別對應X={xg,xp,xh,xw,xa,{weightt},xhc,xbpd,xac,xfl,xafi},隱含層神經元個數為n,輸出層為單個神經元(胎兒體重).

遺傳算法的編碼方式常用的有實數編碼和二進制編碼,其中實數編碼精度高,便于大空間搜索,因此本文采用實數編碼方式. 編碼長度由公式(3)確定.

其中m為輸入層神經元個數,n為隱層神經元個數,l為輸出層神經元個數. 完成編碼過程,選擇合適的初始化種群以及適應度函數計算公式后,進行遺傳算法的選擇、交叉、變異的迭代過程,當迭代過程滿足訓練目標要求或迭代次數達到設定的目標時,停止迭代過程. 將最優的染色體(即神經網絡的初始權值和閾值)作為結果返回.

將遺傳算法的返回結果作為BP神經網絡的初始權值和閾值,完成神經網絡學習過程,得到的最優神經網絡結構即為GA-BPNN胎兒體重預測模型.

3.2 隱含層神經元個數選擇

隱含層神經元個數通過經驗公式(4)確定：

其中,m為輸入層神經元個數,l為輸出層神經元個數,n為隱層神經元個數. 根據公式(4)得到隱含層的節點數應該為5～14. 實驗過程中使用相同的數據集合,每次進行同樣的訓練次數,通過比較均方誤差(MSE)來確定隱含層節點數目. 不同的網絡結構訓練后相應的MSE如表2所示.

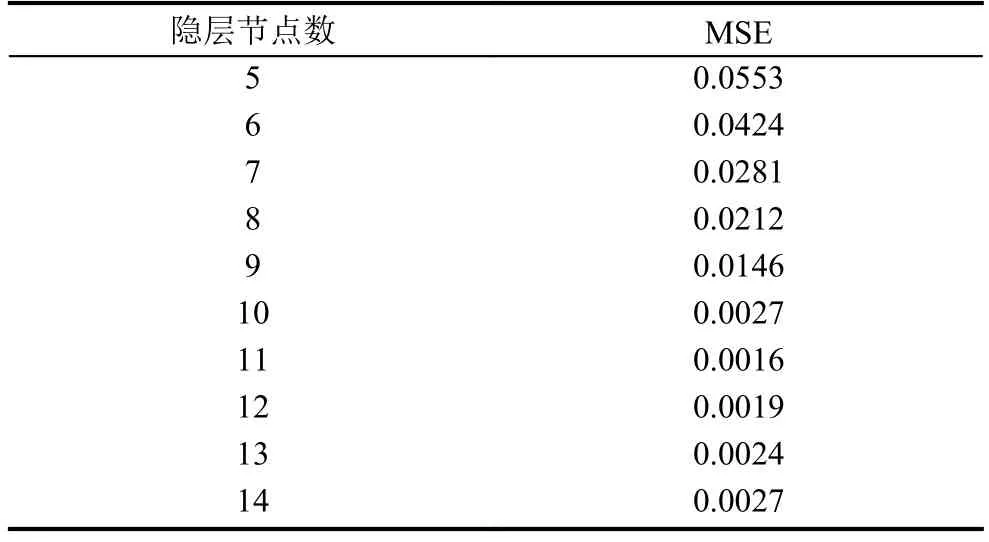
表2 不同網絡結構訓練后的MSE

從表2可知,當隱層節點為11時,網絡性能最好,繼續增加隱層節點數目對提升網絡性能貢獻不明顯,因此確定隱層節點數為11.

3.3 神經網絡優化與訓練

輸入層到隱含層的激活函數使用Relu[15]函數,Relu函數相比于其他激活函數收斂速度快、實現簡單、有效緩解梯度消失問題、在無監督訓練的時候也能有較好的表現. 隱含層到輸出層的激活函數使用線性激活函數.

由于BP神經網絡的閾值和初始權值采用隨機生成的方式,導致BP神經網絡存在收斂速度慢、不能確保收斂到全局最小值等問題. 本文采用遺傳算法優化BP神經網絡的初始權值和閾值,通過處理編碼變量字符串(即染色體)的聚合,可以加速網絡的收斂速度,提升預測模型精度[16]. 在算法中,每個染色體代表待處理問題的個體,并且許多染色體(基本單元)形成遺傳算法的初始種群,通過選擇、交叉、變異三個步驟的操作,將神經網絡從前一代(即父母)群體進化到下一代來完成優化過程.

在本文中,遺傳算法中群體的適應度基于GABPNN與編碼染色體的預測誤差,每個染色體的適應度值(fj)通過式(5)計算：

個體被選擇的概率(Pj)由式(6)計算：

其中,fj是第j個染色體的適應度值,n是神經網絡輸入數據集的數量,m是遺傳算法中種群的大小,eij是第i個神經網絡的輸入與第j個染色體間的誤差.

第二步交叉,將相互配對的父母染色體依據概率交換部分信息,形成下一代. 在交叉的過程中交換的部分是在染色體上隨機選取. 當交叉過程完成后,重新計算每個子代染色體的適應度值,將適應度值高的子代保留在當前種群中.

在將子代染色體重新插入原始群體之前,進行變異過程用來提高遺傳算法的搜索能力和群體多樣性.變異是根據變異概率將染色體中的部分編碼基因改變來實現. 通過該過程,遺傳算法可以更好地搜索整個參數空間,并且可以避免陷入局部最優.

遺傳算法優化BP神經網絡的初始權值和閾值的過程如算法1所示,GA-BPNN模型的訓練過程如算法2所示.

算法1. BP神經網絡初始權值和閾值優化

輸入： 種群大小m; 交叉概率Pc; 變異概率Pm; 迭代次數α

輸出： 最優解x

隨機生成m個解決方案,保存在種群pop中fori= 1 toαdo

精英數量ne=m ·Pc

從pop中選擇最佳的精英ne保存在pop1

//交叉操作,染色體互換部分信息

//保留適應度高的形成下一代

交叉數量nc= (m-ne)/2

forj= 1 toncdo

從pop中隨機選擇兩個解決方案xa和xbfrom

通過對xa和xb交叉操作生成xc和xd

將xc和xd保存在pop2中

endfor

//變異過程,根據變異概率改變部分編碼基因

//避免陷入局部最優

fork=1 toncdo

從pop2中選擇一個方案xk

概率Pm發生變異,并重新生成新的方案xk′

將pop2中的xk更新為xk′

endfor

更新pop=pop1+pop2

endfor

returnxinpop

算法2. GA-BPNN體重預測模型的訓練

輸入： 算法1中的X,Y,x; 學習速率η; 迭代次數m

輸出：Network

//初始化神經網絡結構,輸入神經元15個

//隱含層神經元11個,輸出節點1個

Network← ConstructNetworkLayers()

//將算法1的優化結果賦值給神經網絡權值

weights← x

//利用反向傳播算法更新權重值

fori= 1 tomdo

Outputi← ForwardPropagate(Xi,Network)

BackwardPropagateError(Xi,Outputi,Network)

UpdateWeights(Xi,Outputi,Network,η)

endfor

returnNetwork

4 實驗與結果分析

4.1 實驗對象

本文從我國東部某醫院2016年1月1日至2016年12月31日所有產科電子病歷中隨機抽取了3000例符合實驗要求的樣本. 樣本符合條件為： 單胎、無妊娠綜合征、年齡分布22～43歲、在分娩前72小時內接受過B超檢查. 將樣本集的2250例作為訓練集,剩余750例作為測試集驗證模型預測準確度. 訓練過程中,采用交叉驗證,防止過擬合.

4.2 結果與分析

經試驗選取遺傳算法種群規模為200,交叉概率Pc=0.4、變異概率Pm=0.1,進化代數為100. BP神經網路的學習率選為0.016,誤差精度設置為1×10-3,最大迭代次數3000次. 適應度函數值隨進化代數變化曲線如圖2所示,可以看到個體在進化到83代以后適應度函數值基本沒有變化,到達最大值,取此時的最佳染色體值作為BP神經網絡的初始權值和閾值.

圖2 適應度函數值變化曲線

本文采用兩個指標衡量預測模型的性能. 第一個是平均相對誤差(Mean Relative Error,MRE),該指標更能反映測量的可信程度. 設m為樣本數,MRE為平均相對誤差. 即：

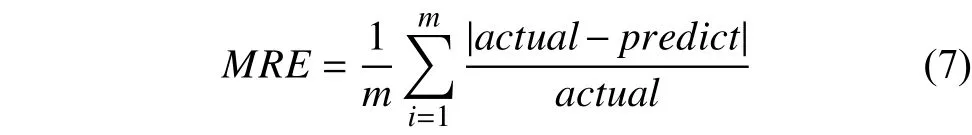
另一種判斷標準為胎兒體重預測值和實際值的誤差在±250克之內即認為預測準確[17],從而計算預測模型的準確率. 通過上述兩種標準來討論本文的實驗結果. 從表3中看出,對胎兒體重的預測GA-BP的誤差控制在6%以內.

表3 兩種神經網絡胎兒體重預測結果(單位： %)

BPNN和GA-BPNN模型的胎兒體重預測誤差統計如表4所示. 其中MiRE為最小相對誤差,MaRE為最大相對誤差,BPNN與GA-BPNN的訓練誤差曲線如圖3所示.

表4 兩種神經網絡模型胎兒體重預測誤差統計(單位： %)

將GA優化后得到的初始權值和閾值賦給神經網絡后,兩種胎兒體重預測模型的預測結果如圖3所示.

圖3 BPNN與GA-BPNN訓練誤差曲線

從表3的結果可知,GA-BPNN比BPNN的預測準確率更高,GA-BPNN的預測結果更加接近胎兒實際體重值. 從圖3可知,GA-BPNN的收斂速度比BPNN的收斂速度快,模型表現更好.

5 結束語

本文提出了一種基于遺傳算法優化BP神經網絡(GA-BPNN)的胎兒體重預測模型,基于孕婦的歷史體檢數據建立連續體征變化模型,然后利用遺傳算法優化BP神經網絡的初始權值和閾值,建立胎兒體重預測模型. 實驗結果表明,本文提出的GA-BPNN胎兒體重預測模型不僅加快了模型的收斂速度,而且將胎兒體重預測精度提高了14%. 未來的工作可以進一步考慮孕婦體檢數據的時間序列特點,改進胎兒體重預測模型,從而進一步提升模型預測的準確率和實用性.

1劉致君,李桂榮,郭興巧. 預測胎兒體重新方法與傳統方法的比較. 中國婦幼保健,2008,23(24)： 3478-3479. [doi：10.3969/j.issn.1001-4411.2008.24.065]

2Yu ZB,Han SP,Zhu JG,et al. Pre-pregnancy body mass index in relation to infant birth weight and offspring overweight/obesity： A systematic review and meta-analysis.PLoS One,2013,8(4)： e61627. [doi： 10.1371/journal.pone.00 61627]

3Shepard MJ,Richards VA,Berkowitz RL,et al. An evaluation of two equations for predicting fetal weight by ultrasound. American Journal of Obstetrics and Gynecology,1982,142(1)： 47-54. [doi： 10.1016/S0002-9378(16)32283-9]

4Hadlock FP,Harrist RB,Carpenter RJ,et al. Sonographic estimation of fetal weight. The value of femur length in addition to head and abdomen measurements. Radiology,1984,150(2)： 535-540. [doi： 10.1148/radiology.150.2.6691 115]

5朱桐梅,趙曉華,艾梅,等. 6種預測胎兒體重公式準確性的對比研究. 中國婦幼保健,2016,31(20)： 4179-4181.

6M?st L,Schmid M,Faschingbauer F,et al. Predicting birth weight with conditionally linear transformation models.Statistical Methods in Medical Research,2016,25(6)： 2781-2810. [doi： 10.1177/0962280214532745]

7洪傳美,紀毅梅. 胎兒體重預測常見方法比較及臨床價值探討. 中國婦幼健康研究,2017,28(5)： 522-523,530.

8刁曉娣,江志斌,劉瑾. 根據孕婦參數預測胎兒體重的神經網絡方法. 中國生物醫學工程學報,1999,18(2)： 155-158,193.

9Farmer RM,Medearis AL,Hirata GI,et al. The use of a neural network for the ultrasonographic estimation of fetal weight in the macrosomic fetus. American Journal of Obstetrics and Gynecology,1992,166(5)： 1467-1472. [doi：10.1016/0002-9378(92)91621-G]

10Cheng YC,Hsia CC,Chang FM,et al. Cluster-based artificial neural network on ultrasonographic parameters for fetal weight estimation. 6th World Congress of Biomechanics(WCB 2010). Singapore. 2010. 1514-1517.

11Mohammadi H,Nemati M,Allahmoradi Z,et al. Ultrasound estimation of fetal weight in twins by artificial neural network. Journal of Biomedical Science and Engineering,2011,4(1)： 46-50. [doi： 10.4236/jbise.2011.41006]

12李昆,柴玉梅,趙紅領,等. 基于深度神經網絡的胎兒體重預測. 計算機科學,2016,43(11A)： 73-76,82.

13Chen GY,Fu KY,Liang ZW,et al. The genetic algorithm based back propagation neural network for MMP prediction in CO2-EOR process. Fuel,2014,(126)： 202-212. [doi：10.1016/j.fuel.2014.02.034]

14Rumelhart DE,Hinton GE,Williams RJ. Learning representations by back-propagating errors. Nature,1986,323(6088)： 533-536. [doi： 10.1038/323533a0]

15Krizhevsky A,Sutskever I,Hinton GE. Imagenet classification with deep convolutional neural networks. Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe,NV,USA. 2012.1097-1105.

16楊啟文,蔣靜坪,張國宏. 遺傳算法優化速度的改進. 軟件學報,2001,12(2)： 270-275.

17難產與圍產編寫組. 難產與圍產. 重慶： 科學技術文獻出版社重慶分社,1983.