基于奇異值分解的Unscented粒子濾波及其應(yīng)用研究

龐　策,　趙　巖

(空軍工程大學(xué)防空反導(dǎo)學(xué)院，西安　710051)

0　引言

非線性濾波[1-3]是針對(duì)非線性系統(tǒng)，解決非線性問題的一種濾波方法，不需要將非線性問題進(jìn)行線性化。常用的非線性濾波方法有：擴(kuò)展卡爾曼濾波(EKF)[4]、中心差分卡爾曼濾波(CDKF)[5]、Unscented卡爾曼濾波(UKF)[6]、高斯-厄米特濾波(GHF)[7]和粒子濾波(PF)[8]等。Unscented粒子濾波(UPF)算法[9]吸收了UKF[4]和PF[1]算法的優(yōu)點(diǎn)，被廣泛用于非線性、非高斯動(dòng)力學(xué)系統(tǒng)的參數(shù)估計(jì)和狀態(tài)濾波問題。UPF算法

不僅克服了UKF算法不適用于非高斯噪聲系統(tǒng)的局限性，而且克服了PF算法重要性密度函數(shù)難以選取的缺陷。但是，UPF算法仍易受到異常擾動(dòng)的影響，且在計(jì)算迭代中可能出現(xiàn)協(xié)方差陣失去半正定性的問題。

針對(duì)UPF算法存在的問題，本文在UPF算法的基礎(chǔ)上，提出基于奇異值分解的Unscented粒子濾波(SVD-UPF)算法。SVDUPF算法采用自適應(yīng)因子調(diào)節(jié)動(dòng)力學(xué)模型誤差，通過奇異值分解抑制系統(tǒng)狀態(tài)協(xié)方差矩陣的負(fù)定性，并以改進(jìn)的UKF算法產(chǎn)生重要性密度函數(shù)，彌補(bǔ)粒子濾波重要性密度函數(shù)難以選取的缺陷。

1　奇異值分解原理

奇異值分解(SVD)是一種重要的矩陣分解方法，是矩陣分析中正規(guī)矩陣酉對(duì)角化的推廣[10-11]。奇異值分解在某些方面與對(duì)稱矩陣或Hermite矩陣基于特征向量的對(duì)角化類似，然而這兩種矩陣分解盡管有其相關(guān)性，但還是存在明顯的不同。對(duì)稱陣特征向量分解的基礎(chǔ)是譜分析，而奇異值分解則是譜分析理論在任意矩陣上的推廣。

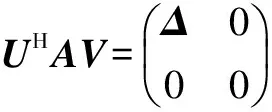
(1)

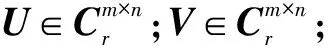
2　基于奇異值分解的Unscented粒子濾波算法

假設(shè)非線性系統(tǒng)

xk=f(xk-1)+wk-1

(2)

zk-1=h(xk-1)+vk-1

(3)

式中：xk為k時(shí)刻系統(tǒng)的n維狀態(tài)向量；……