一種基于頻響函數相似性的鐵路橋墩損傷識別方法

戰家旺，閆宇智，強偉亮，安志剛，張　楠

(1.北京交通大學 土木建筑工程學院，北京　100044；2.中國建筑第六工程局有限公司 技術中心，天津　300000；3.中鐵第五勘察設計院集團有限公司 北京鐵五院工程試驗檢測有限公司，北京　102600)

在列車動力荷載、流水沖刷、環境腐蝕以及車船撞擊等外界作用下，鐵路橋梁下部結構容易出現基礎弱化和結構性損傷等病害，且劣化部位一般在地面或者水面以下。這些劣化部位不能通過外觀檢查及時發現，也很難利用無損檢測和靜力加載等方法對其健康狀態進行評價[1]。目前，我國鐵路橋墩狀態檢定的法定依據是《鐵路橋梁檢定規范》，利用自振頻率和強振響應振幅指標對橋墩的整體性能進行定性評估。部分學者進一步總結了橋墩強振振動的特征，并提出了依據強迫振動波形對病害類型進行初步判斷的方法[2-3]。周海林利用基于模態殘余力向量的損傷因子對焦柳線某橋墩的損傷進行了定位[4]。戰家旺等提出了以自振頻率和振型為輸入的模型修正方法，實現了對橋墩損傷的準確定位和損傷程度定量評價[5]。但實際應用中，由于現場條件、測試技術等方面的制約，以上橋墩評估方法的精度容易受到噪聲等因素的干擾。

近年來，利用頻響函數對結構損傷進行識別成為學者們研究的熱點。例如，Lin和Zhu等[6]利用頻率響應函數頻域幅值通過模型修正方法識別損傷。Ting等[7]以頻響函數為基礎，提出了一種改進的靈敏度計算方法, 通過該計算方法研究基于頻響函數的損傷識別問題。以上方法的基本思路均是通過比較理論與實測頻響函數在頻段內的幅值進行評估。以上方法需要準確的頻響函數幅值，這給其在實際橋梁評估中的應用造成了困難。

本文針對鐵路中廣泛采用的簡支梁橋墩，在損傷識別的目標函數中用測點間頻響函數相似性系數代替頻響函數幅值，提出一種基于模型修正理論和頻響函數相似性的鐵路橋墩損傷識別方法。

1　鐵路橋墩簡化分析模型

根據參考文獻[5]，當圖1(a)所示的鐵路樁基礎或者擴大基礎橋墩產生橫向振動時，可以忽略梁體對橋墩的約束，建立圖1(b)所示的簡化計算模型。該模型中，將橋墩離散成1個多自由度系統，將質量平均分配到模型各個節點上，各節點采用剛度為EI的梁單元進行連接；將上部梁結構簡化為集中質量M置于橋墩頂部；采用扭轉彈簧Kr、水平彈簧Kh和垂直彈簧Kv模擬基礎約束，各方向彈簧剛度根據《鐵路橋涵地基與基礎設計規范》確定。

圖1　橋墩振動分析模型

2　頻響函數相似性系數

當在橋墩墩身k點處施加荷載時，墩身p點處的位移、速度和加速度頻響函數Hpk,u(ω)，Hpk,v(ω)和Hpk,a(ω)分別為

(1)

(2)

(3)

式中：Apr和Akr分別為第r階質量歸一化振型在p點和k點處的幅值；ωr和ξr分別為第r階模態圓頻率和模態阻尼；ω為各頻率點的圓頻率；n為結構的模態階數。

此時，p點q點處的頻響函數向量Hpk和Hqk在某頻率段內的頻響函數相似性系數為

(4)

其中，Hpk=(Hpk(ωl))Tl=1,2，…,m

Hqk=(Hqk(ωl))Tl=1,2，…,m

式中：ωl為選擇頻率段內的第l個圓頻率；m為頻率點個數。

假設測量橋墩振動響應時出現系統誤差，p點和q點處的頻響函數曲線整體幅值分別變為真值的a倍和b倍，代入式(4)得

(5)

可見，頻響函數相似性系數與所選頻率段有直接關系，但不受系統誤差影響。測點間頻響函數相似性系數介于0～1之間，可用來評價頻響函數的形狀吻合程度。當該系數為1時表明2個頻響函數曲線的形狀完全一致，而該系數為0時表明二者完全不相關，該系數的值越大表明二者相似性越好。

3　基于頻響函數相似性的橋墩損傷識別方法

3.1　損傷指標的確定

由于橋墩的動力特性主要由基礎約束剛度、墩身剛度及梁體質量等參數決定。一般情況下，橋墩發生損傷后，其質量不發生改變，僅墩身剛度和基礎約束剛度發生改變。

墩身發生損傷時，假定其慣性矩沒有改變，僅損傷單元處的彈性模量E下降。墩身第j個單元的損傷程度可用損傷度αj(0<αj<1)描述為

(6)

式中：E0j和Edj分別為橋墩第j個單元初始及損傷后的彈性模量，N為單元個數。

基礎發生損傷時，僅其扭轉彈簧剛度和水平彈簧剛度的變化會對橋墩橫向模態和振動響應產生影響，因此可采用扭轉彈簧剛度Kr和水平彈簧剛度Kh的下降模擬損傷，并定義基礎約束損傷度αkr(0<αkr<1)和αkh(0<αkh<1)描述基礎的損傷程度。

(7)

(8)

式中：K0r和K0h分別為基礎的初始扭轉彈簧剛度和水平彈簧剛度；Kdr和Kdh分別為基礎發生損傷后的扭轉彈簧剛度和水平彈簧剛度。

因此，本方法用墩身和基礎損傷度構成橋墩的整體損傷指標向量，即

α=(α1,α2,…,αN,αkr,αkh)

(9)

3.2　目標函數的建立

有限元模型修正的基本思路是對實際結構進行動力測試，同時建立該結構的有限元模型，通過二者的動力學參數建立目標函數，并采用調整有限元模型參數的方法，最終實現實際結構與有限元模型的最大程度吻合。既有模型修正研究中采用的目標函數一般由自振頻率和振型MAC構成，即

(10)

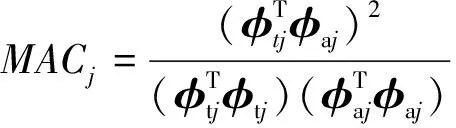
式中：mf和mm分別為采用的自振頻率個數和模態振型個數；fai和fti分別為橋墩第i階理論和實測自振頻率；MACj為有限元模型和實測橋墩第j階模態振型的相似性系數；φtj和φaj分別為第j階實測和理論模態振型；ηi和μj為各子目標函數的權重系數，反映了各子目標函數的重要程度。

基于上述目標函數的計算方法雖然在理論上識別效果較好，但實際應用中，由于測試技術的限制，其識別參數數量和識別精度均容易受到影響。因此，避開易受測點幅值誤差影響的振型參數，以橋墩相鄰測點間頻響函數相似性系數構造目標函數，進行橋墩損傷識別。

當橋墩發生損傷時，其模態參數必然發生變化，同時橋墩不同點間的頻響函數在特定頻段內相似性系數也會發生變化。此時，將鐵路橋墩的墩身離散為N個單元，可得到N個相鄰測點間頻響函數相似性系數。用N個相鄰測點間的頻響函數相似性系數構成向量，即

R=(R(1,2), …,R(i,i+1), …,

R(N,N+1))

(11)

式中：R(i,i+1)為第i個和第i+1個測點之間的頻響函數相似性系數。

由實際橋墩測點和有限元模型節點的頻響函數可分別得實際和有限元模型的橋墩測點間頻響函數相似性系數向量Rt和Ra，進而可得二者的差值向量ΔR，即

ΔR=‖Ra-Rt‖

(12)

當‖ΔR‖趨近于零時，即認為有限元模型可較好地反映結構的實際狀態。

此時，可采用相鄰測點間頻響函數相似性系數代替模態振型相似性系數構造目標函數，即

(13)

式中：mR為相鄰測點對數；ΔR(j,j+1)為有限元模型和實測橋墩第j組相鄰測點間的頻響函數相似性系數之差。

3.3　橋墩損傷的識別

確定了損傷指標，建立了目標函數之后，橋墩損傷識別的過程即為優化求解過程，其實質是將有限元模型修正問題轉化成求解非線性最小二乘問題。為了使修正后參數在合理的范圍內，在計算時引入識別參數的上下限，并使得目標函數最終結果滿足如下收斂準則：

(14)

式中：mm為迭代次數；ε為容許誤差；ξ為容許殘差。

采用上述優化算法對有限元模型的損傷指標進行合理調整，可使目標函數達到最小，并最終達到橋墩結構損傷識別的目的。

4　橋墩損傷識別方法數值驗證

4.1　橋墩數值模擬

為了對提出的橋墩損傷識別方法進行驗證，建立了一矩形橋墩有限元模型，如圖2所示。該模型橋墩截面為0.77 m×0.67 m，墩身高為4.8 m；承臺橫截面為1.8 m×1.4 m，高為0.38 m。墩身混凝土密度為2 600 kg·m-3，彈性模量為32.5 GPa。墩身及承臺平均離散成為9個單元，1#—9#單元為橋墩單元，10#單元和11#單元分別為基底扭轉彈簧單元和水平彈簧單元。基底扭轉彈簧剛度為1.1 GN·(m·rad)-1，水平彈簧剛度為1.0 GN·m-1。

圖2　橋墩數值模型示意圖

針對基礎和墩身兩類病害，設置了4種損傷工況，其中工況1為完整橋墩；工況2為墩身2單元損傷70%；工況3為基底水平向和扭轉彈簧同時損傷60%；工況4為墩身2單元損傷20%、基底水平向和扭轉彈簧同時損傷60%。

各工況條件下橋墩的前2階頻率計算結果見表1。從表1可以看出：當損傷發生時，橋墩各階模態頻率均有一定程度的下降，說明模態頻率對橋墩的損傷較為敏感。

表1　不同工況下橋墩頻率　Hz

4.2　頻帶選擇

橋墩損傷識別結果與所選擇的頻率范圍有直接關系，因此為了分析不同損傷工況下頻響函數相似性系數的變化規律，對不同頻率范圍內的頻響函數相似性進行計算。對于大部分橋墩而言，比較容易測得前2階自振頻率，因此計算頻譜相似性系數時，選擇前2階頻率附近的4個不同頻率段進行分析，結果見表2。

表2　頻響函數頻率段選擇

不同頻段內各損傷工況與無損橋墩的頻譜相似性系數差值如圖3所示。

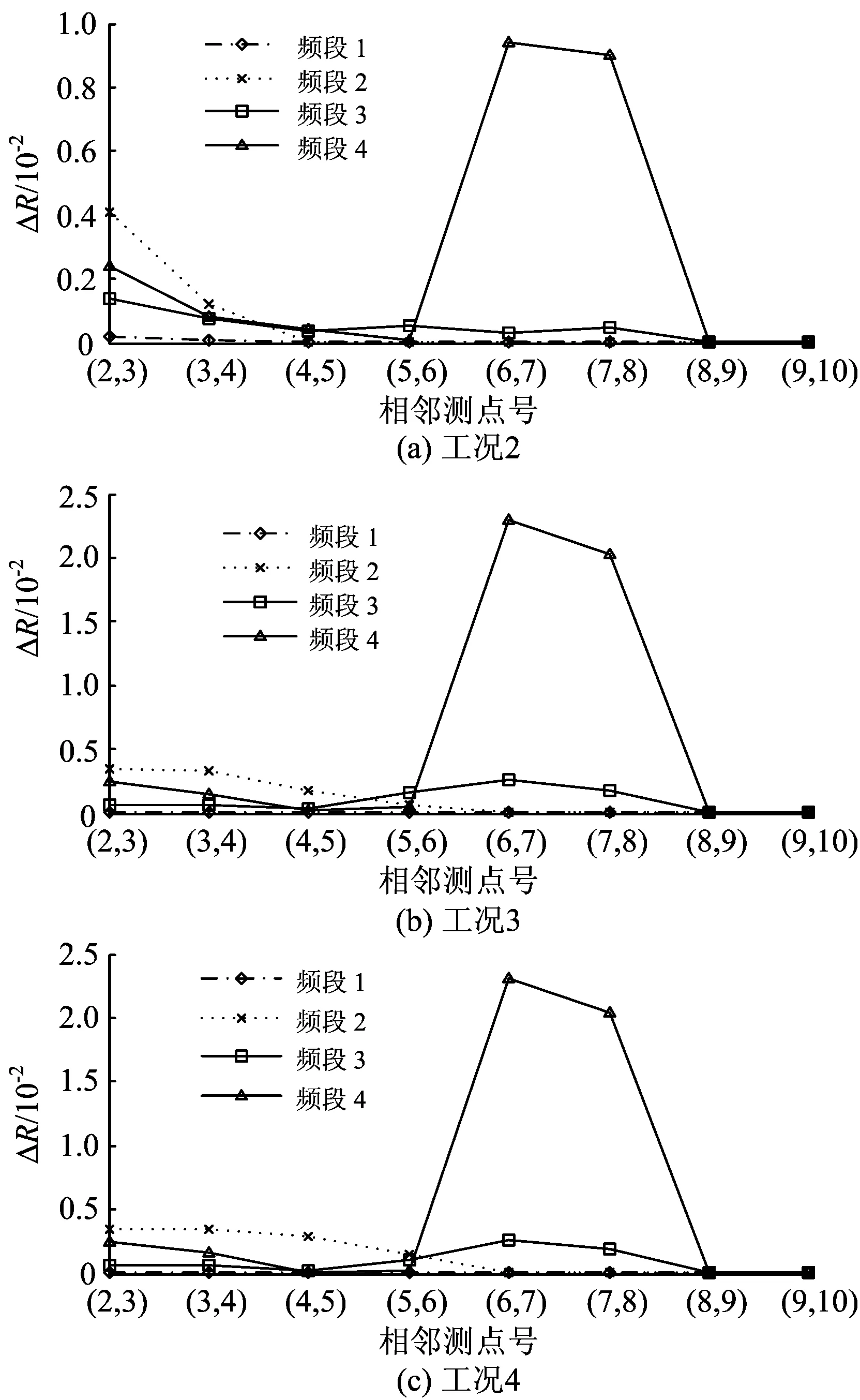
圖3　各頻段下相鄰測點頻譜相似性系數對比

由圖3可見，選擇頻率段1時，各損傷工況的頻譜相似性系數R的差值均接近于0，說明在該頻率段下系數R對損傷敏感性較低；選擇頻率段2時，墩身中部以下各相鄰測點頻譜相似性系數R對損傷較為敏感，中部以上靈敏度較低；選擇頻率段3和頻率段4時，墩身各相鄰測點頻譜相似性系數R對損傷均有一定的靈敏度，且頻率段4對損傷的靈敏度大于頻率段3，因此選擇包含前2階自振頻率在內的頻率段對橋墩進行損傷識別。

4.3　橋墩損傷定量識別

模態頻率是工程中最常用，也是測量最為準確的模態參數，然而由于技術條件、測量水平和信號分析手段的制約，在實際動力測試中，很難測得橋墩3階及以上的高階模態。因此，為保證本文研究方法的工程應用價值，將橋墩的前2階頻率納入目標函數。

在實際橋梁結構中，墩身病害主要出現在橋墩根部和基礎，因此在后續的計算分析中僅對墩身2#—5#單元和基底的10#和11#單元進行損傷識別。

在墩頂施加沖擊荷載，拾取各節點響應，應用本文方法對上述橋墩損傷工況進行識別，結果如圖4所示。由圖4可以看出，各工況下橋墩設定的損傷均得到了正確識別。

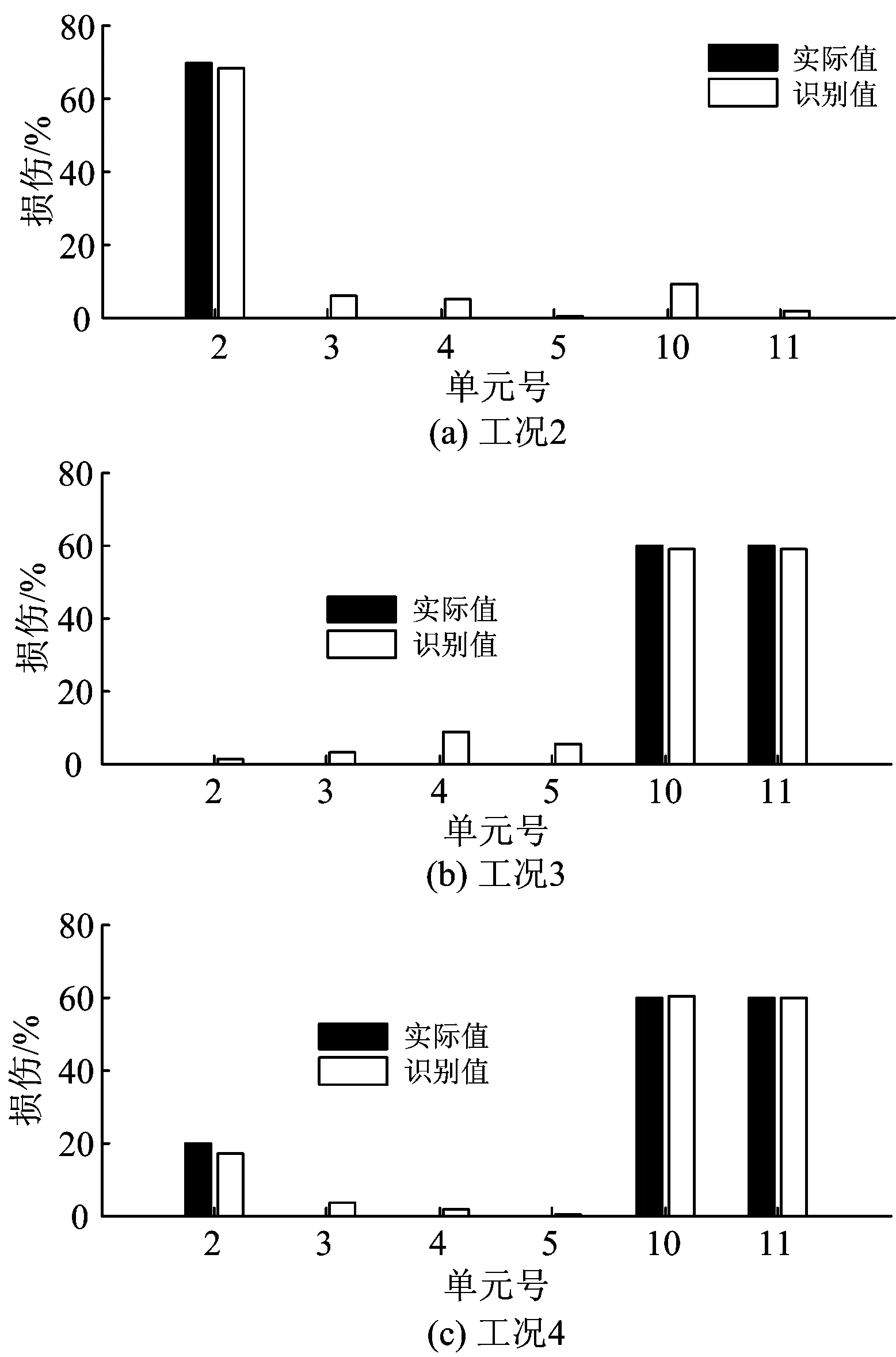
圖4　各工況橋墩損傷識別結果

損傷工況4下損傷指標隨迭代次數的變化過程如圖5所示。由圖5可以看出，本文所提方法的迭代效率較高，僅需10次左右迭代即可收斂到實際損傷值。

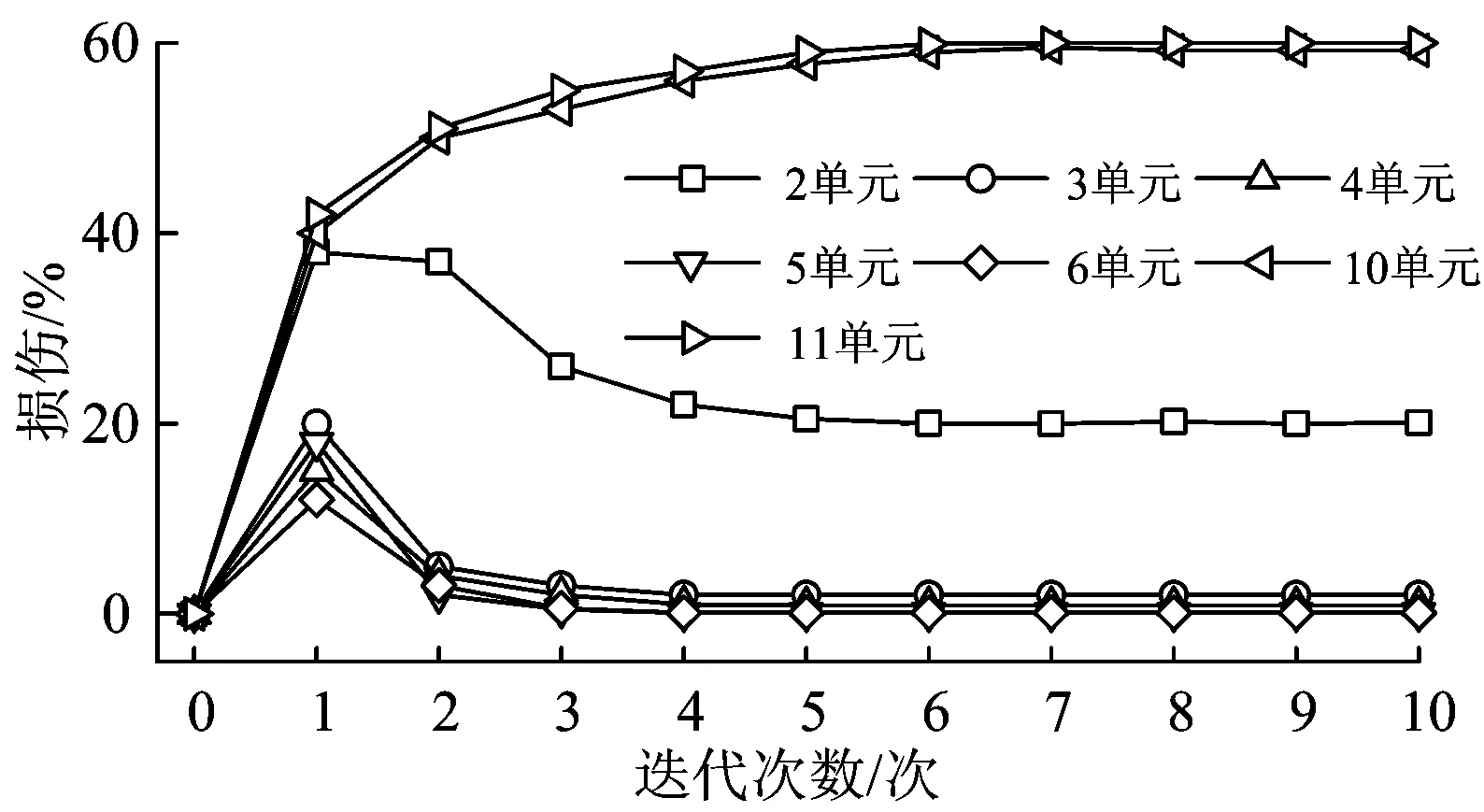
圖5　工況4下優化迭代過程

5　橋墩損傷識別方法模型試驗驗證

由于影響橋墩模型修正質量與損傷識別精度的因素多而復雜，實際測試結果往往會與數值模擬結果存在差異。因此本文設計并加工了橋墩模型，進行相應的試驗分析，從應用角度對所提出方法的可行性與可靠性進行驗證。

5.1　模型橋墩及損傷設計

采用鋼筋混凝土材料建造一矩形懸臂橋墩模型[8]，模型包括墩身，承臺和基礎固定裝置3部分，如圖6所示，各部件尺寸同第3節數值模型。

圖6　模型橋墩

為了模擬橋墩各部位的損傷，對橋墩模型設置如下工況：(1)用螺栓結合大工字鋼，并對橋墩模型底部進行了固定，如圖7所示，模擬無損傷狀態下完整橋墩；(2)如圖8所示，去除基底固定螺栓及工字鋼，模擬橋墩基底損傷；(3)使用千斤頂在墩頂處施加擬靜力荷載直至橋墩發生明顯破壞，并去掉基底約束，模擬墩身與基底同時損傷的病害情況，如圖9所示。

5.2　試驗系統及裝置

試驗中，用聚能力錘對模型橋墩施加沖擊力如圖10所示。拾取圖10各個測點的加速度響應，測點位置與第3節中數值模型相同。

圖7　橋墩完整模型

圖8　橋墩基底損傷模型

圖9　墩身損傷模型

圖10　現場沖擊橋墩

5.3　橋墩模態參數識別

通過對測得的沖擊力時程和各測點響應進行分析，求得橋墩各個測點的頻響函數。圖11為測點9的頻響函數曲線。由圖11可以看出，識別出的完整橋墩狀態下的前2階模態頻率分別為13.25和75.75 Hz。同理可得橋墩基底損傷工況下的前2階模態頻率分別為6.25和50.75 Hz；橋墩基底與墩身同時損傷工況下的前2階模態頻率分別為3.38和15.25 Hz。可見，橋墩損傷后，其各階模態頻率明顯降低。

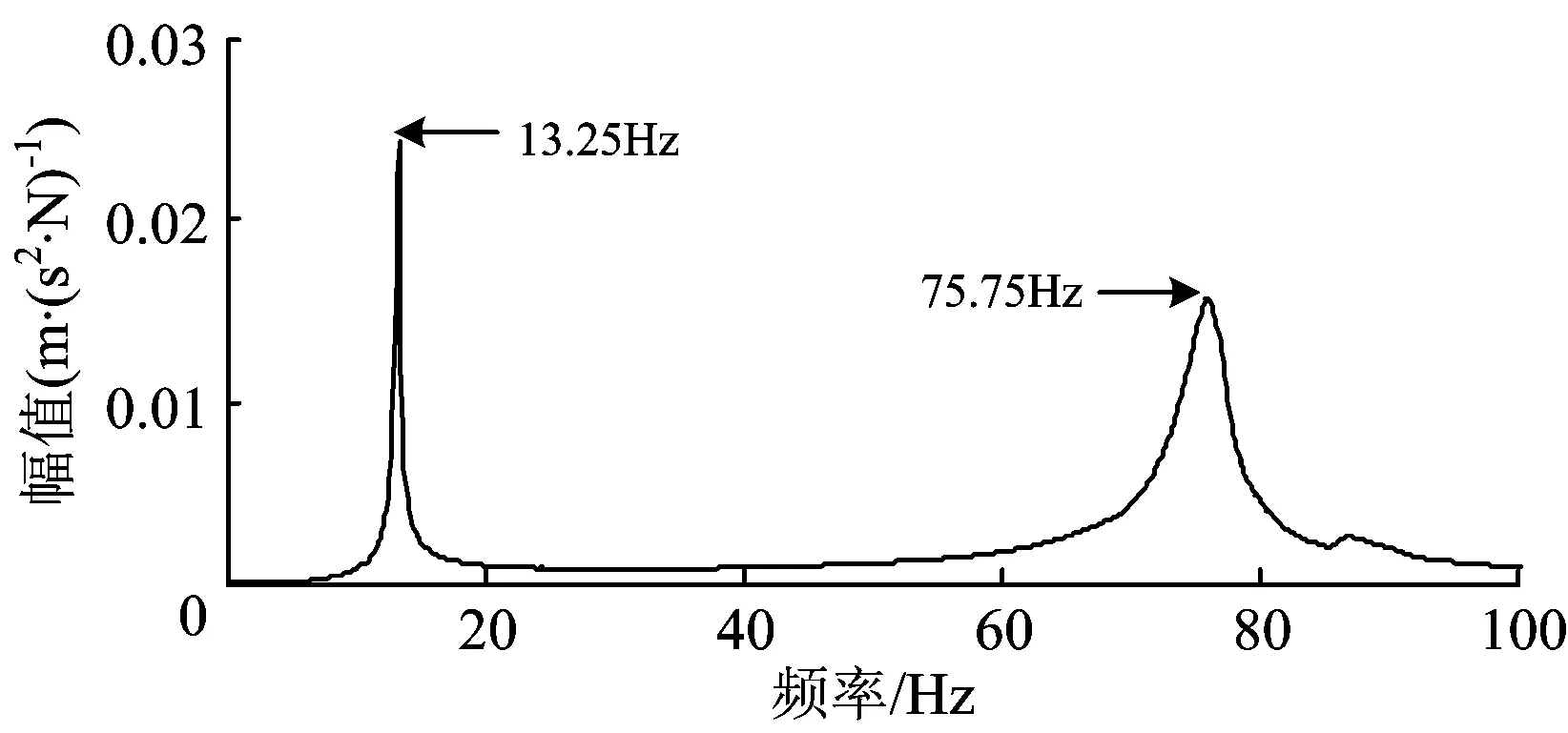
圖11　測點的加速度響應頻響函數

5.4　模型橋墩損傷定量識別

對完整橋墩進行模型修正，獲得其墩身剛度和基底約束剛度初始值。與數值算例類似，取墩身2#—5#單元彈性模量以及基底彈簧剛度作為待修正參數。

表3為完整橋墩模型修正后的各單元剛度。從表3可以看出，修正后墩身彈性模量的平均值約為30 GPa，小于混凝土彈性模量初始值，說明橋墩模型理論剛度大于其實際剛度。而識別出基底彈簧剛度與規范的理論值差別較大，這是由試驗橋墩模型與實際橋墩基底約束條件的差異所導致的。

表3　初始條件下橋墩各單元剛度匹配結果

完整橋墩各單元剛度識別后，將其修正值設定為有限元修正模型的初始參數，即墩身單元彈性模量初值為30 GPa；基底扭轉彈簧剛度初值為0.77 GN·(m·rad)-1；基底水平彈簧初值為2.9 GN·m-1。進而進行其他工況下的損傷識別。

橋墩基底損傷工況下的識別結果如圖12所示。由圖12可以看出：基底10#和11#彈簧單元的損傷最為明顯，達到了80%以上，這是由于基底固定螺栓的去除使得橋墩基底約束減弱導致的；其他墩身單元出現了6%左右的虛假損傷。

圖13為基底與墩身共同損傷時的識別結果。由圖13可以看出：墩身底部2#和3#單元的損傷度達到75%，4#—5#單元損傷度較小，表明墩身底部加載破壞后，相應位置處的剛度下降較為明顯，墩身其他單元沒有明顯破壞，與實際情況相符；基底損傷度與圖12接近，說明2種損傷工況下基底的約束狀態并未發生明顯變化，這也與實際情況相吻合。

圖12　橋墩基底損傷識別結果

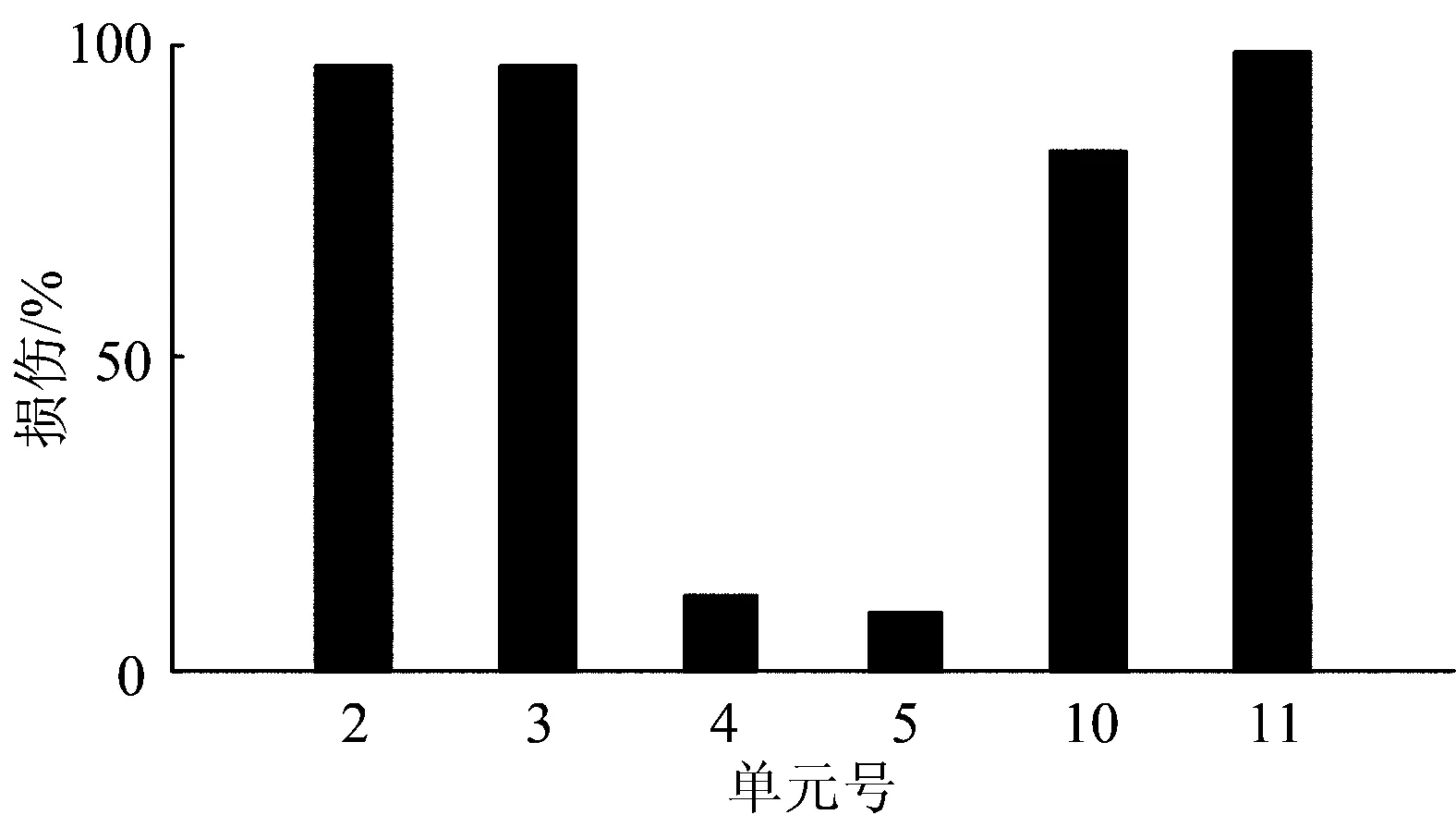
圖13　墩身與基底同時病害條件下識別結果

綜合以上識別結果可以看出，雖然在一些未損單元會存在一定程度的虛假損傷，但橋墩損傷識別結果能夠較好反映橋墩的實際損傷情況，表明本文所提出的方法具有較好的實際應用效果。

6　結　論

(1) 提出了一種基于模型修正理論和相鄰測點頻響函數相似性系數的鐵路橋墩損傷識別方法，該方法不受系統誤差影響，可有效提高模型修正時待識別參數的數量，且計算效率高，僅需10次左右迭代即可達到收斂。

(2) 包含第1和第2階頻率在內的頻率段對橋墩損傷比較敏感，采用該頻率段內的頻響函數相似性系數可對橋墩損傷進行精確定位和定量識別。

(3) 對某模型橋墩進行了實驗室試驗，對設定的損傷進行了識別。試驗結果表明識別損傷與實際損傷吻合較好，從而證明了本文所提方法的實用性。

[1]崔飛，袁萬城，史家鈞.基于靜載試驗進行橋梁結構損傷識別[J].橋梁建設，2003,2(4):4-7.

(CUI Fei, YUAN Wancheng, SHI Jiajun. Bridge Structural Damage Identification Based on Static Test[J]. Bridge Construction, 2003,2(4):4-7.in Chinese)

[2]孫國藩. 探測鐵路橋梁墩臺損傷方法的研究[R]. 哈爾濱：哈爾濱鐵路局, 1989.

[3]陳新中，周宏業.鐵路橋墩病害振動診斷方法的研究[J].中國鐵道科學，1987,8(1):20-33.

(CHEN Xinzhong, ZHOU Hongye. Research on the Vibration Diagnostic Method of Railway Bridge Pier’s Faults[J]. China Railway Science, 1987,8(1):20-33.in Chinese)

[4]周海林,王星華. 橋墩病害動力測試分析[J]. 中國鐵道科學, 2001, 22(5):128-132.

(ZHOU Hailin, WANG Xinghua. Analysis of the Pier Damage by Dynamic Experiment [J]. China Railway Science, 2001, 22(5): 128-132.in Chinese)

[5]戰家旺, 王偉, 張楠，等. 基于模型修正理論的鐵路橋墩損傷定量評估方法[J]. 中國鐵道科學, 2015,36(5): 28-35.

(ZHAN Jiawang, WANG Wei, ZHANG Nan, et al. Quantitative Damage Evaluation Method for Railway Piers Based on Model Updating Theory [J]. China Railway Science, 2015,36(5): 28-35.in Chinese)

[6]LIN R M, ZHU J. Model Updating of Damped Structures Using FRF Data [J]. Mechanical Systems and Signal Processing, 2006, 20: 2200-2218.

[7]TING T. Design Sensitivity Analysis of Structural Frequency Response [C]// AIAA-92-4799-CP, 4th AIAA/USAF/NASA/OAI Symposium on Multidisciplinary Analysis and Optimization, 1992, 878-881.

[8]安志剛. 基于動力參數的鐵路橋墩損傷識別方法研究[D]. 北京:北京交通大學,2014.

(AN Zhigang. Study on Damage Identification Method for Railway Piers Based on Dynamic Parameters[D]. Beijing: Beijing Jiaotong University,2014. in Chinese)