Stewart平臺多能域系統(tǒng)動力學(xué)全解建模與實驗

李永泉　劉天旭　王立捷　張立杰　程雪利

(1.燕山大學(xué)河北省并聯(lián)機(jī)器人與機(jī)電系統(tǒng)實驗室， 秦皇島 066004；2.燕山大學(xué)先進(jìn)鍛壓成形技術(shù)與科學(xué)教育部重點實驗室， 秦皇島 066004；3.燕山大學(xué)河北省重型機(jī)械流體動力傳輸與控制實驗室， 秦皇島 066004; 4.河南工學(xué)院機(jī)械工程系， 新鄉(xiāng) 453002)

0　引言

并聯(lián)機(jī)構(gòu)的動力學(xué)模型是對其進(jìn)行動力學(xué)分析、動力學(xué)優(yōu)化以及動力學(xué)參數(shù)辨識的基礎(chǔ)，而且準(zhǔn)確的動力學(xué)模型是對機(jī)構(gòu)高速高精度控制的前提。牛頓-歐拉法、拉格朗日方程法、虛功原理法和凱恩方程法是目前常用的并聯(lián)機(jī)構(gòu)動力學(xué)建模方法。這些方法在Stewart平臺機(jī)構(gòu)的動力學(xué)建模中得到了廣泛的應(yīng)用。文獻(xiàn)[1-3]采用牛頓-歐拉法建立了該平臺的動力學(xué)模型，通過對運動桿件的單獨分析，列出運動桿件的牛頓方程，通過消去中間變量，得到包含關(guān)節(jié)約束力的整體動力學(xué)方程；文獻(xiàn)[4-6]應(yīng)用拉格朗日方程法，依據(jù)系統(tǒng)動能和勢能構(gòu)造拉格朗日函數(shù)，基于運動學(xué)模型計算系統(tǒng)動能、勢能以及廣義力，從而建立Stewart平臺只包含驅(qū)動力而并沒有關(guān)節(jié)約束力的動力學(xué)模型；文獻(xiàn)[7-10]采用虛功原理建立了該平臺動力學(xué)模型，引入虛位移和虛功的概念，基于慣性力和驅(qū)動力所做虛功之和為零這一基本思想，得到多剛體系統(tǒng)的動力學(xué)模型；鹿玲等[11]利用凱恩方程法對5UPS/PRPU進(jìn)行動力學(xué)建模。李兵等[12]采用凱恩方程法對Stewart平臺進(jìn)行動力學(xué)建模，基本思想是廣義慣性力和廣義主動力之和為零，從而得到系統(tǒng)不含約束力的動力學(xué)方程。李鷺揚等[13]利用凱恩方程建立了Gough-Stewart平臺的高效動力學(xué)模型。此外，F(xiàn)IJANY等[14]提出了一種新的算法，利用投影矩陣將平臺的速度、加速度信息與關(guān)節(jié)的速度、加速度信息直接關(guān)聯(lián)，建立了平臺的動力學(xué)模型。以上方法都是針對機(jī)構(gòu)本體建立的單一能域的動力學(xué)模型，而機(jī)器人系統(tǒng)本身可能包含伺服電機(jī)、液壓缸、電動缸等驅(qū)動部分的一種或幾種組合，本身屬于多能域耦合系統(tǒng)。經(jīng)典的動力學(xué)建模方法局限于并聯(lián)機(jī)構(gòu)機(jī)械部分本體的動力學(xué)建模，若要構(gòu)建系統(tǒng)多能域全局動力學(xué)模型，需要對各個能域包含的子系統(tǒng)分別建模，建立中間變量將各個系統(tǒng)聯(lián)系起來解，這就增加了動力學(xué)狀態(tài)方程變量的數(shù)目，并使建模過程變得十分復(fù)雜，降低了模型的準(zhǔn)確性。

為解決多能域子系統(tǒng)之間的相互作用，功率鍵合圖(Bond graph)理論于1959年由PAYNTER[15]提出。經(jīng)過KARNOPP等[16-17]的研究，鍵合圖理論日益完善。針對Stewart并聯(lián)機(jī)構(gòu)，先后有DAMIC等[18]、YILDIZ等[19]采用功率鍵合圖構(gòu)建了包含驅(qū)動電機(jī)在內(nèi)的鍵合圖模型，并推導(dǎo)了平臺的狀態(tài)方程。但是由于Stewart平臺分支較多且屬于一個空間多自由度、多體系統(tǒng)，其鍵合圖模型復(fù)雜度高、耦合性強(qiáng)，采用傳統(tǒng)鍵合圖理論建立的機(jī)構(gòu)動力學(xué)模型復(fù)雜。為此，文獻(xiàn)[20-21]在機(jī)構(gòu)動力學(xué)建模過程中引入旋量理論，綜合了旋量理論在描述空間構(gòu)件以及鍵合圖理論在多能域動力學(xué)建模的優(yōu)勢，提出旋量鍵合圖概念。本文綜合旋量理論在描述并聯(lián)機(jī)構(gòu)運動學(xué)方面的優(yōu)勢，結(jié)合鍵合圖理論在動力學(xué)建模方面的簡潔性，對并聯(lián)機(jī)構(gòu)的多能域動力學(xué)進(jìn)行建模。

1　Stewart平臺介紹

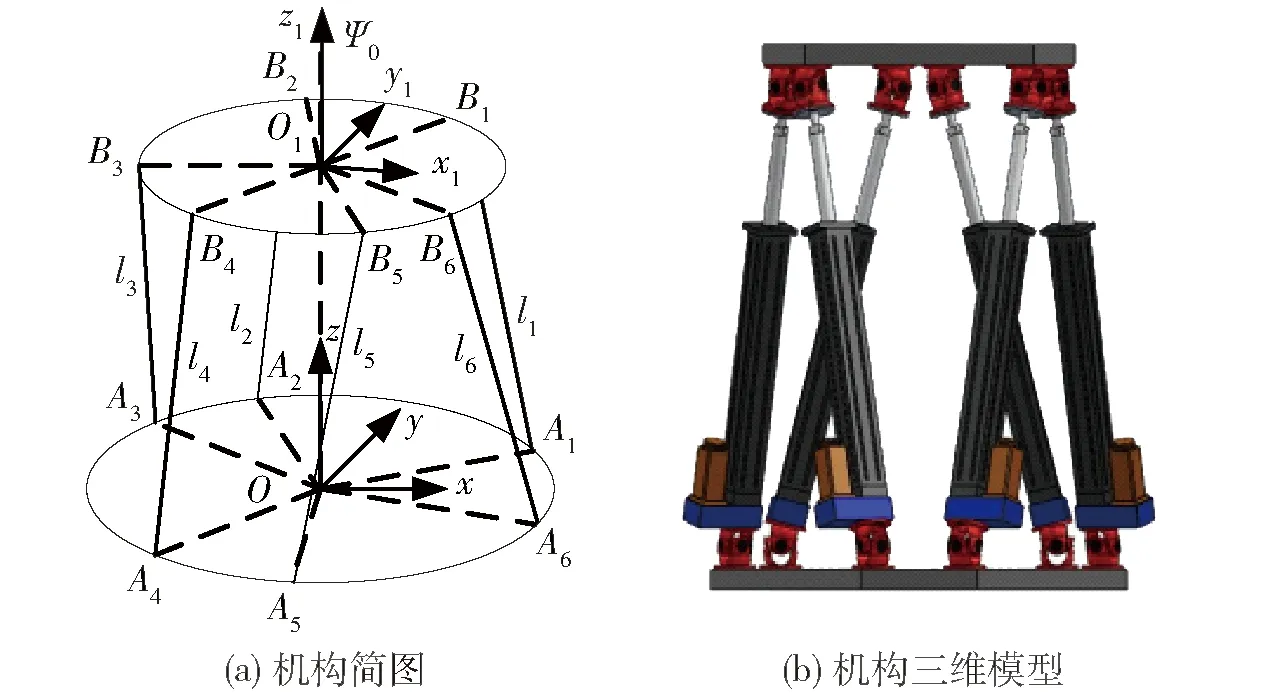
圖1　Stewart平臺Fig.1　Stewart platform

Stewart平臺機(jī)構(gòu)簡圖如圖1a所示，其定平臺上6個萬向鉸U的鉸點用A1,A2,…,A6表示，動平臺上6個球鉸S的鉸點用B1,B2，…，B6表示，定平臺和動平臺通過6個完全相同的UPS支鏈相連，移動副P作為驅(qū)動副，由電動缸實現(xiàn)支鏈的伸縮運動。在定平臺上建立定坐標(biāo)系Oxyz，坐標(biāo)原點O位于萬向鉸所在平面的幾何中心，z軸為過中心點O的豎直軸，它與定平臺所在平面垂直，x軸垂直于A1A6，y軸由右手定則確定。同樣建立動坐標(biāo)系O1x1y1z1，即慣性系Ψ0。坐標(biāo)原點O1位于球鉸所在平面的幾何中心,x1軸垂直于B1B6，z1軸垂直于運動平臺所在平面，y1軸由右手螺旋定則確定。圖1b為Stewart平臺的三維模型。

2　Stewart平臺機(jī)構(gòu)本體旋量鍵合圖模型

2.1　支鏈坐標(biāo)系和動平臺坐標(biāo)系建立

首先建立用于旋量鍵合圖建模的支鏈坐標(biāo)系，如下：

桿件質(zhì)心坐標(biāo)系：簡化驅(qū)動支鏈，假設(shè)支鏈上下連桿的質(zhì)心Cui、Cdi位于支鏈伸縮方向上，如圖2所示，在質(zhì)心處構(gòu)建與慣性系Ψ0各坐標(biāo)軸方向平行的坐標(biāo)系Ψuι、Ψdi。

圖2　驅(qū)動支鏈結(jié)構(gòu)圖Fig.2　Structure diagram of drive chain

支鏈坐標(biāo)系：如圖3所示，在萬向鉸轉(zhuǎn)動中心處，建立支鏈坐標(biāo)系Ψ-i(i=1,2,3,4,5,6)，坐標(biāo)原點為Ai，其z-軸沿支鏈伸縮方向由Ai指向Bi，y-軸垂直于平面OAiBi，沿z1負(fù)方向作為順時針方向，則x-=y-z-。

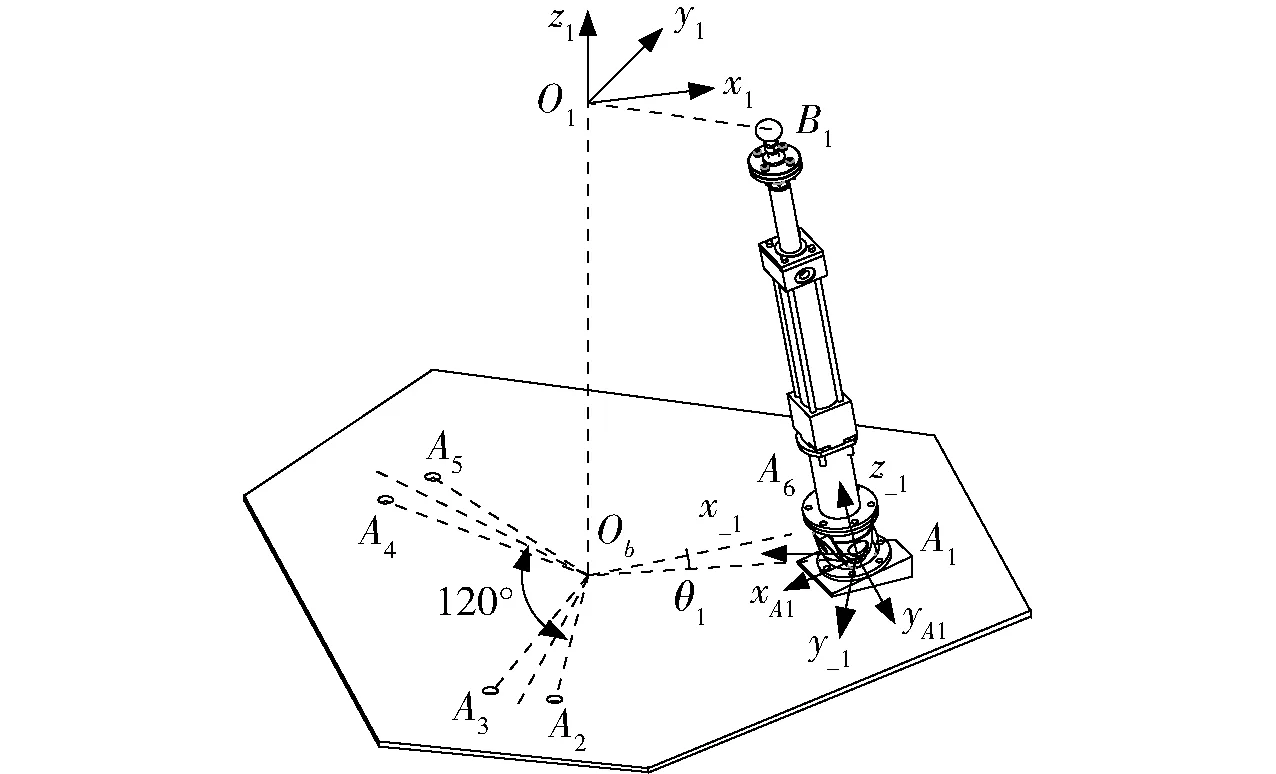
圖3　驅(qū)動支鏈分布圖Fig.3　Distribution diagram of drive chain

運動副接觸坐標(biāo)系：首先，在萬向鉸轉(zhuǎn)動中心Ai處建立萬向鉸接觸坐標(biāo)系ΨAi(i=1,2,3,4,5,6)，令yAi軸方向為萬向鉸十字軸軸線的方向，分布如圖3所示，xAi軸垂直于yAi軸和支鏈伸縮方向si構(gòu)成的平面，即xAi=yAisi，則zAi=xAiyAi；接著，分別在電動缸活塞桿和缸體接觸點Ki和球鉸轉(zhuǎn)動中心Bi處，建立移動副接觸坐標(biāo)系ΨKi和球鉸接觸坐標(biāo)系ΨBi，各坐標(biāo)軸方向平行于支鏈坐標(biāo)系Ψ-i的各坐標(biāo)軸方向。

假設(shè)機(jī)構(gòu)動平臺受作用在E點載荷We，如圖4所示。以E點為原點，建立與慣性系Ψ0平行的載荷坐標(biāo)系ΨE。

圖4　動平臺組件結(jié)構(gòu)圖Fig.4　Structure diagram of moving platform

2.2　Stewart平臺機(jī)構(gòu)本體旋量鍵合圖建模

Stewart平臺的運動組件可視為由驅(qū)動支鏈組件和動平臺組件兩部分組成，其中驅(qū)動支鏈組件由移動副即伺服電缸、萬向鉸、球鉸及測力傳感器組成；動平臺組件由動平臺及球鉸安裝楔塊組成。分別對這兩部分進(jìn)行旋量鍵合圖建模。

根據(jù)文獻(xiàn)[20]建立UPS支鏈旋量鍵合圖，如圖5所示。由于萬向鉸連接定平臺，速度為0，因此采用0流源作為輸入；而球鉸連接動平臺，通過鍵②/③/④/⑤/⑥/⑦，將驅(qū)動支鏈旋量鍵合圖連接到動平臺旋量鍵合圖。鍵①則表示連接到電動缸驅(qū)動子系統(tǒng)鍵合圖。建立動平臺旋量鍵合圖模型，如圖6所示。

根據(jù)圖5驅(qū)動支鏈鍵合圖模型，列寫驅(qū)動支鏈的狀態(tài)方程

(1)

圖6　動平臺旋量鍵合圖Fig.6　Screw bond graph of moving platform

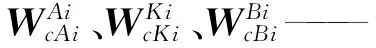
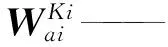
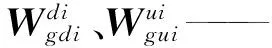
mdi、mui——支鏈下、上連桿的質(zhì)量

根據(jù)圖6動平臺鍵合圖模型，可得動平臺狀態(tài)方程為

(2)

式(1)、(2)分別是驅(qū)動支鏈以及動平臺的狀態(tài)方程，即Stewart平臺機(jī)構(gòu)本體動力學(xué)模型，共包含78個未知量，對應(yīng)的可以列出78個狀態(tài)方程，可以得到該平臺機(jī)構(gòu)本體的動力學(xué)全解。

2.3　Stewart平臺機(jī)構(gòu)本體逆向動力學(xué)仿真

平臺機(jī)構(gòu)的逆向動力學(xué)模型是分析其動態(tài)性能及參數(shù)辨識的基礎(chǔ)，基于機(jī)構(gòu)的旋量鍵合圖得到的狀態(tài)方程，利用Matlab編程軟件和ADAMS動力學(xué)仿真軟件對其動力學(xué)模型進(jìn)行仿真驗證。

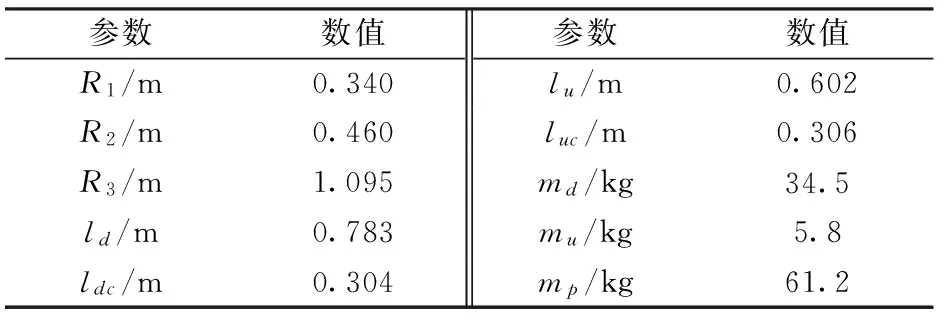
表1　Stewart平臺部分參數(shù)Tab.1　Part of Stewart platform parameters

為使機(jī)構(gòu)工作空間最大，令機(jī)構(gòu)初始姿態(tài)為ψ=0°、φ=0°、θ=0°。采用組合正弦函數(shù)[22]對末端運動軌跡進(jìn)行軌跡規(guī)劃，末端運動軌跡如圖7所示，通過反解計算得到電動缸的運動學(xué)信息，如圖8所示。

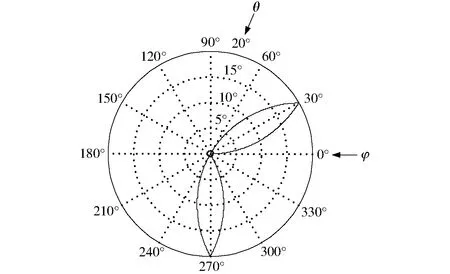
圖7　末端P的運動軌跡Fig.7　Trajectory of end P

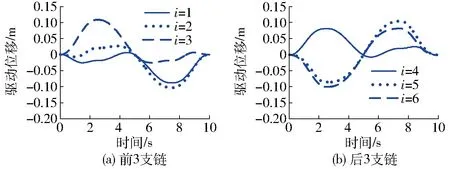
圖8　驅(qū)動位移Fig.8　Drive displacement

根據(jù)機(jī)構(gòu)的運動學(xué)信息和狀態(tài)方程，利用Matlab軟件計算得到機(jī)構(gòu)驅(qū)動力，如圖9所示；同時，建立機(jī)構(gòu)三維模型，利用ADAMS軟件對其進(jìn)行仿真，仿真驗證模型如圖10所示，得到機(jī)構(gòu)驅(qū)動力如圖11所示。對比圖9和圖11，由于在理論計算中忽略了球鉸及萬向鉸等構(gòu)件的慣量，從而使得理論值與仿真值產(chǎn)生了微小偏差。但是，誤差相對于驅(qū)動力數(shù)值很小，因此可以驗證基于旋量鍵合圖得到的動力學(xué)模型的準(zhǔn)確性。

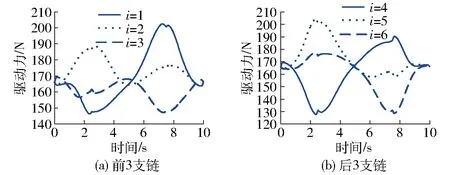
圖9　理論計算驅(qū)動力Fig.9　Theory value of driving force

圖10　ADAMS仿真模型Fig.10　Simulation mode in ADAMS

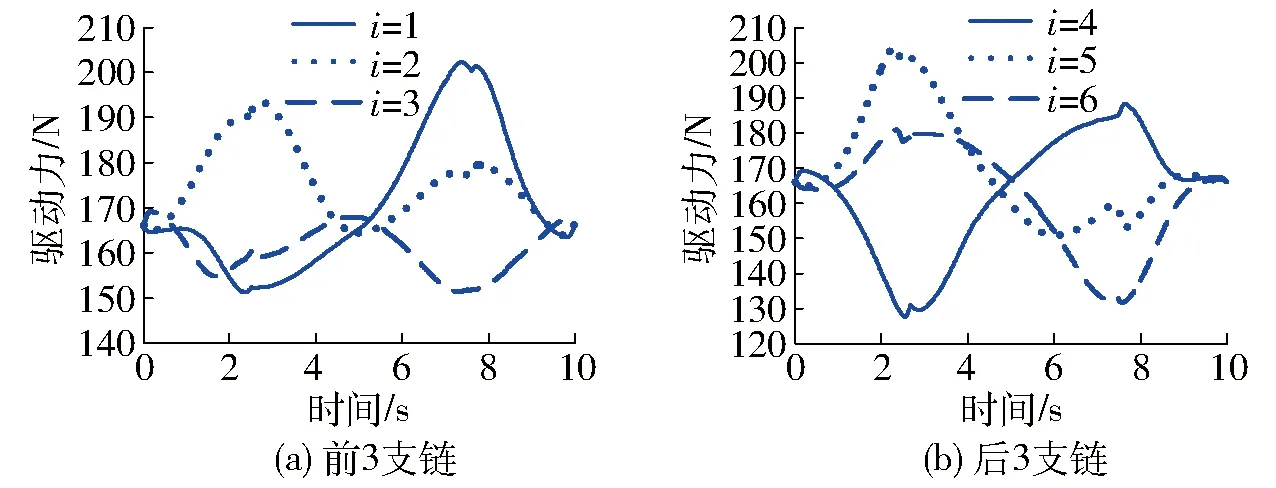
圖11　仿真驅(qū)動力Fig.11　Driving force of simulation

基于旋量鍵合圖模型得到的狀態(tài)方程，動力學(xué)全解除了6條支鏈的驅(qū)動力之外，還包括任意時刻萬向鉸、移動副和球面副處的約束力。驅(qū)動支鏈各個關(guān)節(jié)約束力變化如圖12～14所示。

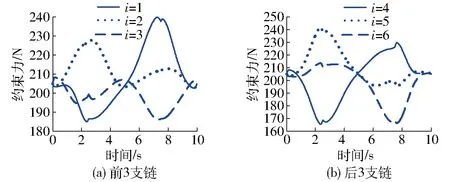
圖12　萬向鉸處約束力Fig.12　Constraint force of universal joints

圖13　球鉸處約束力Fig.13　Constraint force of spherical joints

圖14　移動副處約束力Fig.14　Constraint force of translational joints

3　Stewart平臺多能域系統(tǒng)動力學(xué)模型

3.1　伺服電動缸鍵合圖模型

Stewart平臺采用電動缸作為執(zhí)行機(jī)構(gòu)。電動缸是將伺服電機(jī)與絲杠一體化設(shè)計的模塊化產(chǎn)品，伺服電機(jī)轉(zhuǎn)子的旋轉(zhuǎn)運動通過滾珠絲杠機(jī)構(gòu)轉(zhuǎn)化為推桿的直線運動。其工作原理如圖15所示。伺服電機(jī)及滾珠絲杠機(jī)構(gòu)采用傳統(tǒng)鍵合圖建模，鍵合圖模型如圖16所示。

圖15　電動缸物理模型Fig.15　Physical model of electric cylinder

圖16　電動缸鍵合圖模型Fig.16　Bonding graph model of electric cylinder

分別選取p和q作為狀態(tài)變量，則狀態(tài)方程為

(3)

式中La——電機(jī)電樞電感

Ra——電機(jī)電樞電阻

Ja——電機(jī)轉(zhuǎn)子以及同步帶輪慣量

Ta——電機(jī)電磁轉(zhuǎn)矩常量

Tf——滾珠絲杠導(dǎo)程

K——滾珠絲杠扭矩剛度，為無窮大

3.2　Stewart平臺多能域系統(tǒng)動力學(xué)模型

將Stewart平臺機(jī)構(gòu)本體旋量鍵合圖與伺服電動缸驅(qū)動系統(tǒng)鍵合圖結(jié)合，建立完整Stewart平臺機(jī)、電耦合的多能域系統(tǒng)動力學(xué)全解模型，如圖17所示。

依據(jù)式(1)～(3)，運行圖7所示軌跡，可理論計算電機(jī)電流變換情況，如圖18所示。對比圖9與圖18可以看出，電機(jī)電流和驅(qū)動力呈一定的比例關(guān)系，這符合伺服電動缸的特點，此外，電機(jī)電流的變化曲線的峰值并未超過所選電機(jī)的額定電流，可以驗證所選伺服電機(jī)在此工況下滿足要求。

4　實驗

在加工完成Stewart平臺機(jī)構(gòu)樣機(jī)的基礎(chǔ)上，選取輔助的實驗設(shè)備，完成平臺機(jī)構(gòu)本體動力學(xué)驗證實驗。實驗樣機(jī)和控制系統(tǒng)如圖19所示，實驗設(shè)備結(jié)構(gòu)如圖20所示。

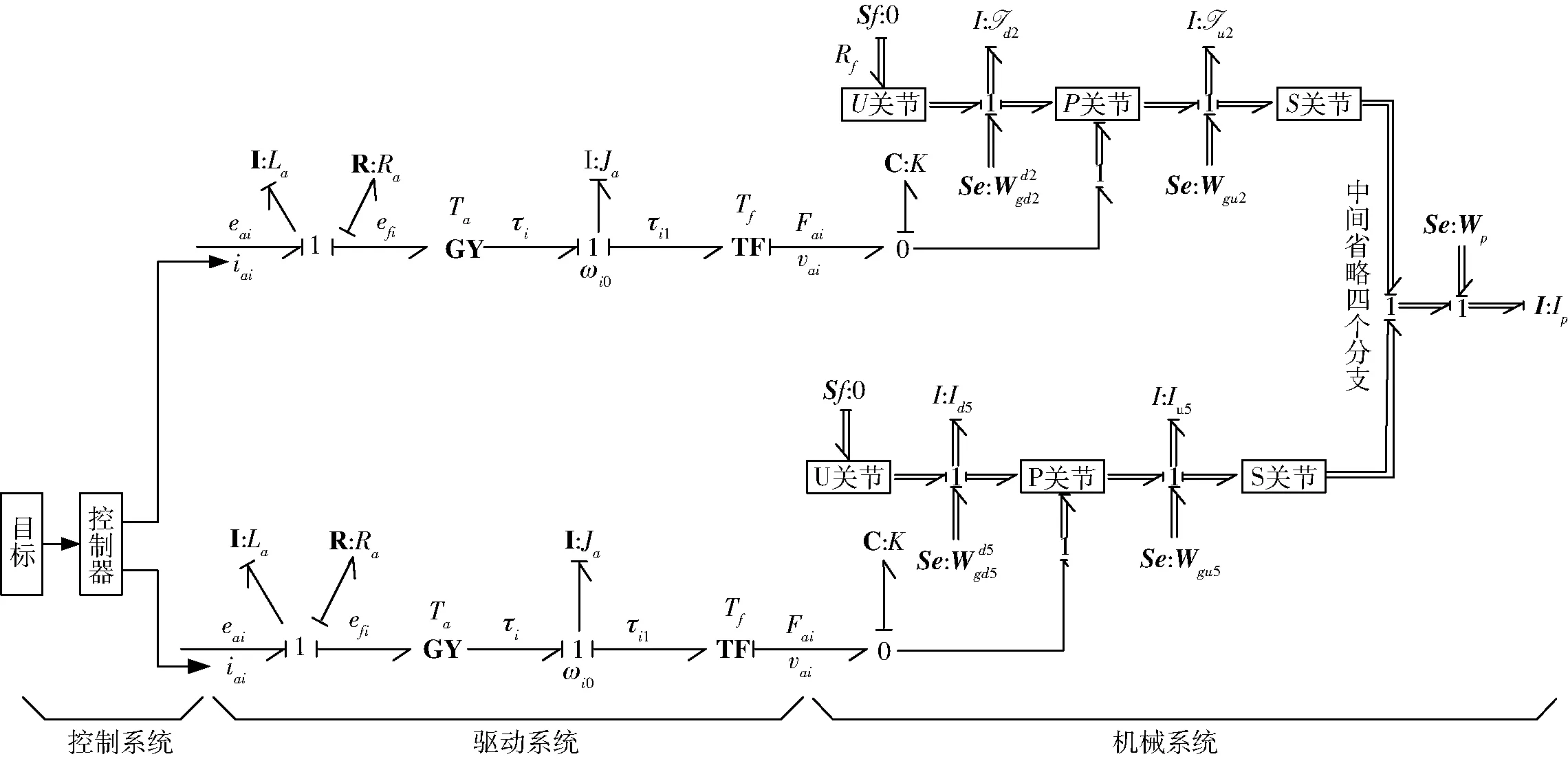
圖17　Stewart平臺機(jī)、電耦合的多能域系統(tǒng)動力學(xué)全局模型Fig.17　Model of multi-energy domain dynamics of Stewart platform, which was mechanical and electronic coupling systems

圖18　電機(jī)電流理論計算值Fig.18　Theory value of motor current

圖19　實驗系統(tǒng)Fig.19　System of experiment

圖20　實驗裝置Fig.20　Device of experiment

其中，控制器選用倍福公司生產(chǎn)的C6920-0050型控制器，伺服電機(jī)選用的是中達(dá)電通公司的ECMA-C11010SS型伺服電機(jī)，電動缸選用上海漣恒公司伺服電動缸，型號為AH75-S500-B-T-10-M3-C1-2，物理參數(shù)如表2所示，力傳感器的型號為LH-S50。

表2　電動缸的物理參數(shù)Tab.2　Physical parameters of electric cylinder

4.1　Stewart平臺機(jī)構(gòu)本體動力學(xué)驗證實驗

圖21　機(jī)構(gòu)位姿Fig.21　Position of mechanism

令機(jī)構(gòu)運行圖7所示軌跡，機(jī)構(gòu)不同位姿如圖21所示，通過力傳感器采集數(shù)據(jù)，并進(jìn)行濾波處理，得到驅(qū)動力數(shù)據(jù)的實測值，和理論計算值進(jìn)行對比，結(jié)果如圖22所示。對比圖22、圖9、圖11，三者符合度較高，從而證明基于旋量鍵合圖所得機(jī)構(gòu)本體動力學(xué)模型的正確性。

圖22　驅(qū)動力理論值與實測值對比Fig.22　Comparisons of driving force between theory and measured values

4.2　Stewart平臺機(jī)構(gòu)多能域動力學(xué)模型驗證實驗

將數(shù)據(jù)線一端連接驅(qū)動器，一端連接裝有與所選臺達(dá)電機(jī)配套的ASDA-SOFT軟件的計算機(jī)，通過軟件中的示波器，讀取實驗電機(jī)電流，并將數(shù)據(jù)保存為.TXT格式的文件，和理論計算值進(jìn)行對比，結(jié)果如圖23所示，兩者誤差較小，從而驗證了Stewart平臺多能域系統(tǒng)動力學(xué)全解模型的正確性。

圖23　電機(jī)電流實測值與理論值對比Fig.23　Comparisons of motor current between measured and theory values

5　結(jié)束語

采用旋量鍵合圖建立了電動缸驅(qū)動Stewart平臺機(jī)構(gòu)本體動力學(xué)模型，采用傳統(tǒng)鍵合圖建立了伺服電動缸鍵合圖模型，得到了該平臺完整的機(jī)、電耦合的多能域系統(tǒng)動力學(xué)全解模型；并通過仿真分析與設(shè)計實驗兩方面驗證了平臺機(jī)電耦合多能域系統(tǒng)動力學(xué)全解的正確性，為后續(xù)包含驅(qū)動單元慣性參數(shù)和摩擦參數(shù)在內(nèi)的動力學(xué)參數(shù)辨識以及平臺控制研究奠定了基礎(chǔ)。

1DASGUPTA B, MRUTHYUNJAYA T S. A Newton-Euler formulation for the inverse dynamics of the Stewart platform manipulator[J]. Mechanism & Machine Theory, 1998, 33(8):1135-1152.

2KHALIL W, GUEGAN S. A novel solution for the dynamic modeling of Gough-Stewart manipulators[C]∥Proceedings of the 2002 IEEE International Conference on Robotics and Automation, 2002, 1:817-822.

3KHALIL W, IBRAHIM O. General solution for the dynamic modeling of parallel robots[J]. Journal of Intelligent & Robotic Systems, 2007, 49(1):19-37.

4WANG J, GOSSELIN C M. A new approach for the dynamic analysis of parallel manipulators[J]. Multibody System Dynamics, 1998, 2(3):317-334.

5ABDELLATIF H, HEIMANN B. Computational efficient inverse dynamics of 6-DOF fully parallel manipulators by using the Lagrangian formalism[J]. Mechanism & Machine Theory, 2009, 44(1):192-207.

6呂幫俊, 彭利坤, 邢繼峰,等. Gough-Stewart并聯(lián)機(jī)器人剛體動力學(xué)模型[J]. 華中科技大學(xué)學(xué)報：自然科學(xué)版, 2011, 39(10):14-18.

Lü Bangjun, PENG Likun, XING Jifeng, et al. Rigid dynamic model of Gough-Stewart parellel robot[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2011, 39(10):14-18. (in Chinese)

7TSAI L W. Solving the inverse dynamics of a Stewart-Gough manipulator by the principle of virtual work[J]. Journal of Mechanical Design, 2000,122(1):3-9.

8STAICU S. Dynamics of the 6-6 Stewart parallel manipulator[J]. Robotics and Computer-Integrated Manufacturing, 2011, 27(1):212-220.

9呂幫俊, 朱石堅, 邢繼峰,等. 基于虛功原理的Stewart機(jī)構(gòu)逆動力學(xué)模型修正[J]. 機(jī)械設(shè)計與研究, 2010, 26(4):42-44.

Lü Bangjun, ZHU Shijian, XING Jifeng, et al. Modification of the invers dynamics model of Stewart robot by the principle of virtual work[J]. Machine Design & Research, 2010, 26(4):42-44. (in Chinese)

10張東勝, 許允斗, 姚建濤,等. 五自由度混聯(lián)機(jī)器人逆動力學(xué)分析[J/OL]. 農(nóng)業(yè)機(jī)械學(xué)報, 2017，48(9):384-391. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20170949&journal_id=jcsam.DOI：10.6041/j.issn.1000-1298.2017.09.049.

ZHANG Dongsheng, XU Yundou, YAO Jiantao, et al. Inverse dynamics analysis of novel 5-DOF hybrid robot[J/OL]. Transactions of the Chinese Society for Agricultural Machinery，2017，48(9):384-391.(in Chinese)

11鹿玲, 姚建濤, 顧偉棟,等. 基于Kane方程的冗余驅(qū)動5UPS/PRPU并聯(lián)機(jī)床動力學(xué)分析[J/OL]. 農(nóng)業(yè)機(jī)械學(xué)報, 2016, 47(6):366-372.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160648&journal_id=jcsam.DOI：10.6041/j.issn.1000-1298.2016.06.048.

LU Ling, YAO Jiantao, GU Weidong, et al. Dynamics analysis of 5UPS/PRPU parallel machine tool with redundant actuation based on Kane equation[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(6):366-372. (in Chinese)

12李兵, 王知行, 李建生. 基于凱恩方法的新型并聯(lián)機(jī)床動力學(xué)研究[J]. 機(jī)械科學(xué)與技術(shù), 1999, 18(1):41-43.

LI Bing, WANG Zhixing, LI Jiansheng. Dynamic study of new parallel machine tool based on Kane method[J]. Mechanical Science and Technology for Aerospace Engineering, 1999, 18(1):41-43. (in Chinese)

13李鷺揚, 吳洪濤, 朱劍英,等. Gough-Stewart平臺高效動力學(xué)建模研究[J]. 機(jī)械科學(xué)與技術(shù), 2005, 24(8):887-889.

LI Luyang, WU Hongtao, ZHU Jianying, et al. Study on the dynamic modeling of Gough-Stewart platform[J]. Mechanical Science and Technology for Aerospace Engineering, 2005, 24(8):887-889. (in Chinese)

14FIJANY A, FRIED G. Novel algorithms for computation of inverse kinematics and inverse dynamics of Gough-Stewart platform[C]∥IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2012:1573-1580.

15PAYNTER H M. Analysis and design of engineering systems[M]. Cambrige: M.I.T. Press, 1961.

16KARNOPP D C, MARGOLIS D L, ROSENBERG R C. System dynamics: modeling, simulation and control of mechatronic Systems[M]. New York: John Wiley & Sons, Inc., 2012:12-20, 53-58, 142-149, 256-259.

17KARNOPP D C, MARGOLIS D L, ROSENBERG R C. System dynamics: modeling and simulation of mechatronic systems[M]. New York: John Wiley & Sons, Inc., 2006.

18DAMIC V, COHODAR M. Dynamic analysis of Stewart platform by bond graphs[J]. Procedia Engineering, 2015, 100:226-233.

19YILDIZ I, OMURLU V E, SAGIRLI A. A novel visualization technique in bond-graph method for modeling of a generalized Stewart platform[C]∥2008 IEEE International Conference on Robotics and Biomimetics, 2008:780-785.

20郭菲, 李永泉, 宋肇經(jīng),等. 旋量鍵合圖在并聯(lián)機(jī)構(gòu)動力學(xué)建模中的應(yīng)用[J]. 機(jī)械工程學(xué)報, 2015, 51(23):12-20.

GUO Fei, LI Yongquan, SONG Zhaojing et al. Screw bond graph in the application of the parallel mechanism dynamics modeling[J]. Journal of Mechanical Engineering, 2015, 51(23):12-20. (in Chinese)

21BONDERSON L S. Vector bond graphs applied to one-dimensional distributed systems[J]. Journal of Dynamic Systems Measurement & Control, 1975, 97(1):75-82.

22李永泉. 球面2-DOF并聯(lián)機(jī)構(gòu)的理論分析與實驗研究[D]. 秦皇島：燕山大學(xué), 2012:75-76.

LI Yongquan. Theory analysis and experiment research of spherical 2-DOF parallel manipulator[D]. Qinhuangdao:Yanshan University, 2012:75-76. (in Chinese)