基于雙磁鋼轉子的大力矩飛輪用電機設計*
王 勇,王 超,張云環,王 森,聶 周
(1.上海航天控制技術研究所·上海·201109;2.上海慣性工程技術研究中心·上海·201109)
0 引 言
目前,衛星上使用的飛輪電機大多數采用直流無刷電機,其具有結構簡單、線性機械特性、寬調速范圍等特點。另外采用空心杯定子,消除了鐵芯帶來的齒槽效應轉矩。伴隨著衛星姿態的大角度機動和快速敏捷要求,衛星姿態控制執行機構采用的飛輪要求具有大的輸出力矩,一般不低于0.5Nm。為實現大力矩的輸出,僅依靠增加電機的外形尺寸或增大線圈匝數來增大輸出力矩是不現實的,這樣會帶來電機外形尺寸過大,從而導致整個飛輪結構尺寸偏大、結構布局不合理、質量偏大;另外,如果電機轉子直徑較大,容易與其外圍的輪體產生干涉,結構設計困難;若增大氣隙,可以避免結構干涉問題,但會導致氣隙磁密降低,從而減小電磁力矩的輸出。因此,面對飛輪大力矩輸出的要求,采用傳統的直流無刷電機已有局限性。
1 工作原理
在電機尺寸限定的條件下,單純增加線圈匝數來提高輸出力矩,在工藝上已不可操作,而通過內部磁路結構的變化,增大氣隙磁密則是一種增大輸出力矩的有效方式[1-2]。
本文提出了一種大力矩飛輪用雙磁鋼轉子電機,其最大輸出力矩不小于1Nm。每對極磁路是由內、外共4個永磁體串聯起來提供磁動勢。永磁體產生的磁通路徑如圖1所示。圖1中,1為外轉子;2為外磁鋼;3為氣隙;4為內磁鋼;5為內轉子。磁力線由外磁鋼N極出發,通過外層氣隙到達定子線圈,并進入內層氣隙正對的內磁鋼S極。再由內磁鋼N極出發,經內轉子到達相鄰內磁鋼S極,并經內磁鋼N極穿過內層氣隙到達定子線圈,進入外層氣隙正對的相鄰外磁鋼S極。再由相鄰外磁鋼N極,經外轉子回到外磁鋼S極,并到達外磁鋼N極,磁力線由此形成了一個閉合回路。根據電磁力定律,由于定子線圈內外層所受電磁力沿圓周方向一致,為內、外兩電機力矩疊加的形式,所以可以增大輸出力矩。當飛輪對永磁直流電機供電時,定子兩相繞組切斷磁力線。根據電磁轉矩原理,將使轉子相對于定子產生旋轉運動,驅動轉子產生角動量和輸出反作用力矩,將電能轉變為機械能[3]。
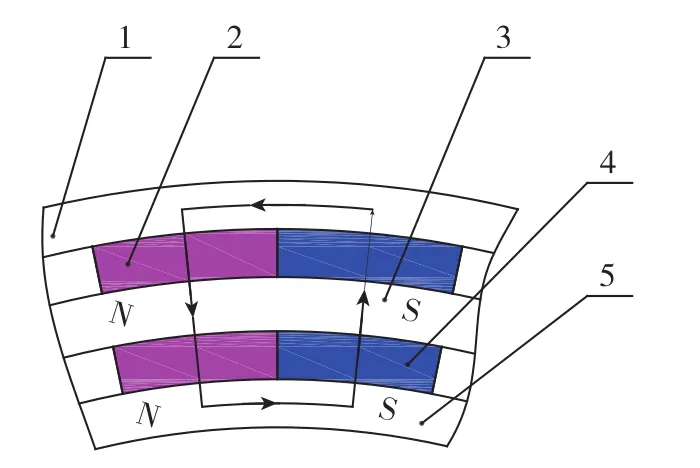
圖1 磁路結構圖
2 結構組成
雙磁鋼電機為分體式結構,包括轉子組件和定子組件。轉子組件由外轉子、外磁鋼、內轉子、內磁鋼和磁鋼壓塊組成,如圖2所示,轉子組件通過外轉子與飛輪軸承座同軸間隙配合,并采用螺釘聯接,可為飛輪提供一部分轉動慣量。定子組件由定子繞組、定子骨架和定子支架組成,如圖3所示,定子組件通過定子支架與飛輪同軸聯接。
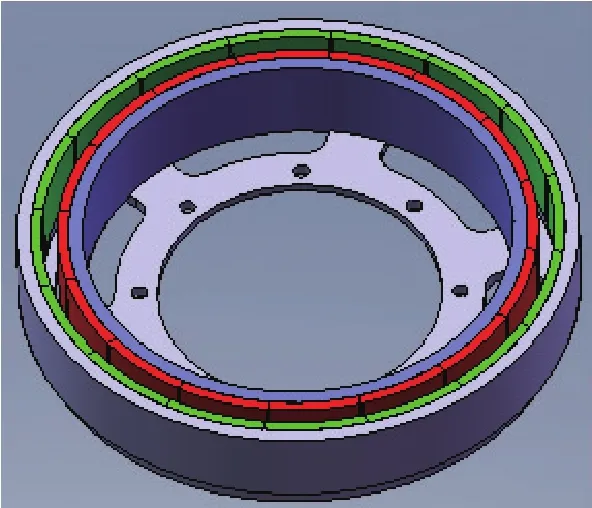
圖2 轉子組件

圖3 定子組件
外轉子和內轉子均采用電工純鐵,具有良好的導磁性能;外磁鋼和內磁鋼采用釤鈷永磁體,具有穩定的溫度特性和較大的剩磁和矯頑力,其結構為瓦片形結構。外轉子端面設有減重槽,內側設有定位槽。裝配時,首先將外轉子與內轉子同軸螺釘聯接。然后將外磁鋼通過磁拉力和粘結劑,均布固連在外轉子內環面上,磁鋼之間N、S間隔裝配,并用外壓塊鍥緊,保證牢固;同理,再通過專用工裝將內磁鋼均布貼于內轉子外環面上,磁鋼之間N、S間隔裝配,保證牢固。在同一徑向尺寸,外磁鋼2與內磁鋼的極性相反,并保持同心安裝。最后,將整個轉子組件通過外轉子,與飛輪軸承座同軸螺釘聯接。
定子組件采用空心杯結構,由線圈粘結在定子骨架上,并通過高強度環氧樹脂灌澆注在定子座上。定子骨架采用非金屬材料,取代了傳統的鐵芯,消除了渦流損耗,提高了電氣效率。
3 主要技術研究
3.1 幾何尺寸確定
1)轉子尺寸的確定
電機轉子尺寸確定的基本原則如下[4]:
①尺寸方程是建立在電機轉子外表面所占有的總體積上;
②引入波形系數量化電機不同的電流波形和相反電勢波形的效應;
③引入電機的體積密度、質量密度、系數和熱量面密度作為轉子設計方評估的依據。
依據以上原則,忽略定子漏電感和電阻后,電機的輸出功率方程可表示為[5]
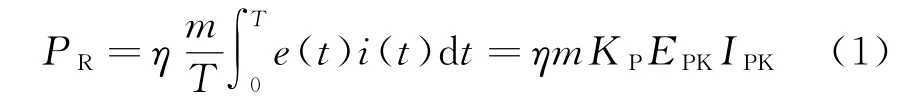
式中:e(t)和EPK為電機相電勢及其峰值;i(t)和IPK為電機相電流及其峰值;η為電機效率;m為電機相數;T為電功率周期;KP為電功率波形系數,其定義為
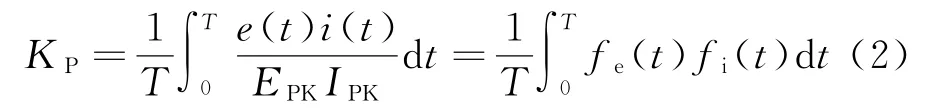
式中:fe(t)=e(t)/EPK為相反電勢波形表達式;fi(t)=i(t)/IPK為相電流波形表達式。
電機的相反電勢為
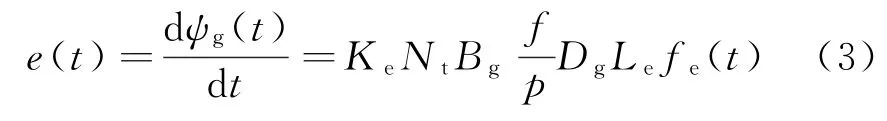
式中:ψg為每相繞組的磁鏈;Nt為每相繞組的匝數;Bg為氣隙磁通密度的峰值;f為逆變器的工作頻率;p為電機極對數;Ke為電勢系數,該系數包括定子繞組分布系數KW和磁極的極弧系數α;Dg為氣隙處直徑;Le為轉子軸向長度。
從式 (3)可得電機的相反電勢峰值為
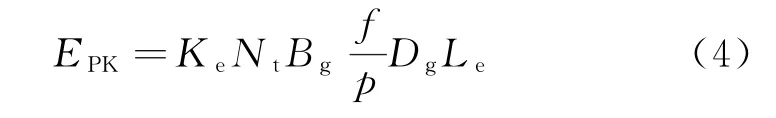
為計及電流波形的熱效應定義電流波形系數為
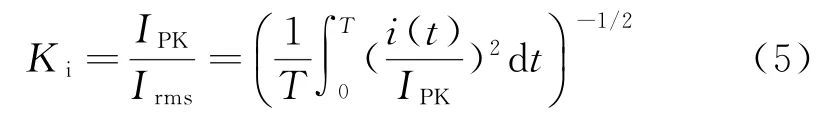
式中:Irms為電機相電流的均方根值,其取值決于定子繞組的線負荷AS
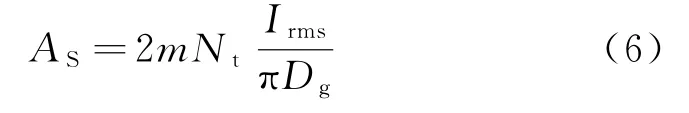
由式 (5)、式 (6)即得電機的相電流峰值表達式
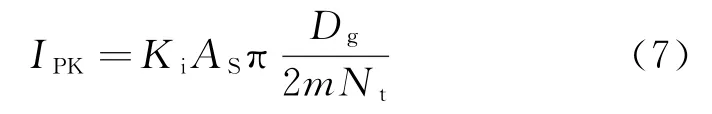
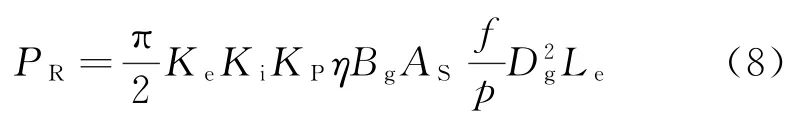
2)永磁體尺寸的確定
永磁體采用釤鈷磁鋼,磁鋼采用扇形瓦片狀結構。其尺寸和電機的轉子磁路結構決定了電機的磁負荷,而磁負荷則決定著電機的功率密度和損耗。對于表面式轉子磁路結構永磁電機,其永磁體尺寸可近似地由式 (9)確定:
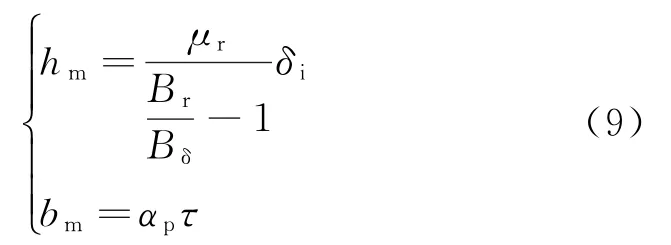
式中,δi為氣隙長度;Br為剩磁;Bδ為氣隙磁密;τ為極矩。
為了抑制力矩波動,可以改變傳統的磁鋼平行充磁方式,采用磁鋼徑向充磁,會獲得較平坦的氣隙磁場分布和較平的反電勢波形,從而降低力矩波動。另外,可適當增加磁鋼極對數,使力矩波動的頻率提高,一般來說低頻的力矩波動對衛星姿態的影響較大。
3.2 電機有限元模型
該電機的磁路由外轉子、外磁鋼、內磁鋼、內轉子和氣隙組成,氣隙磁場計算是電機計算之關鍵。有限元模型包括所有的節點、單元、材料屬性、邊界條件,以及其他用來表現這個物理系統的特征[6],有限元仿真的前處理主要包括:創建模型、設置邊界條件、施加勵磁及負載、模型的網格剖分和設置計算步長[7]。本電機的極/槽數為32/24,為此求解區域選為1/8個電機。取樣機的有限元求解模型及網格剖分圖如圖4、圖5所示。計算步長的選擇也是影響分析計算精度的關鍵因素。為提高計算精度,盡量減小計算步長,但步長過小會造成計算量過大,對計算機CPU和內存要求太大,計算時間也過長。因此,為了兼顧計算精度和計算時間,需根據經驗合理選擇步長。
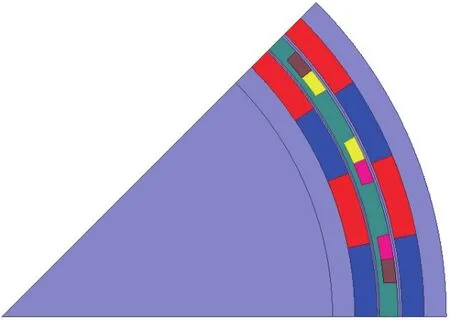
圖4 雙磁鋼轉子電機的求解模型
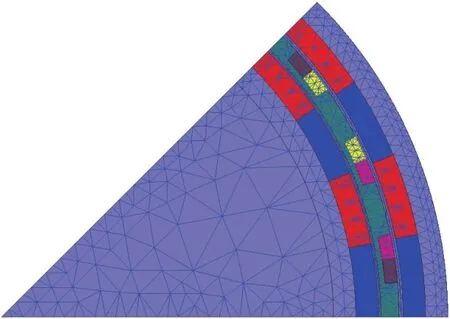
圖5 網格剖分
3.3 仿真分析
1)電機空載性能分析計算
雙磁鋼轉子電機空載時,電樞繞組中沒有電流,即ia=ib=ic=0A,磁場由內、外轉子中永磁體產生,通過有限元計算便可得到空載磁場的計算結果,仿真轉速n=1200r/min,得出2對極下電機的磁力線仿真結果,如圖6所示。
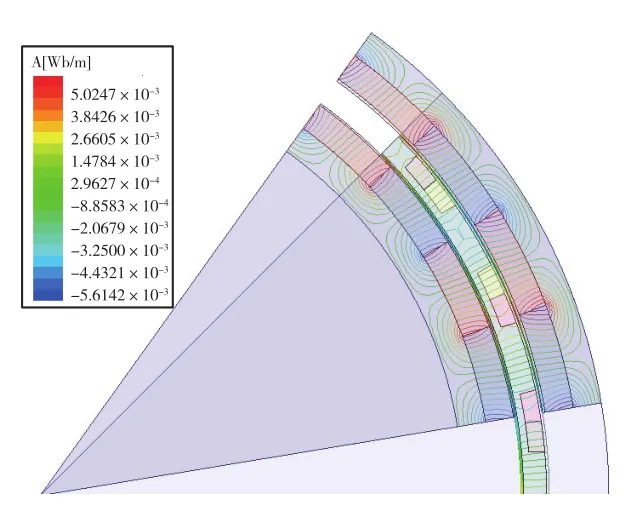
圖6 磁力線分布
圖6顯示了電機的磁力線分布,從圖中可以看出,永磁磁通路徑與原理定性分析相一致。
圖7、圖8和圖9分別給出了空載轉速n=1000r/min,2對極中軸向位置z=0處內、外轉子氣隙磁密波形圖和樣機磁密分布圖。由圖7和圖8可知,內、外轉子空載氣隙磁密波形一極下基本為一平頂波,平均值為0.59T、0.56T(絕對值)。氣隙磁密分布不是光滑的曲線,而是類似于正弦波的曲線[8]。由于采用了雙磁鋼的結構,氣隙磁場有明顯增強,氣隙磁密分布如圖9所示。在相同力矩條件下,可以減小定子線圈的切割軸向長度,從而減少銅損;并可以同步減小轉子組件的軸向長度,從而減小整個飛輪的軸向長度,補償內磁鋼增加的質量,實現整體結構的輕量化。
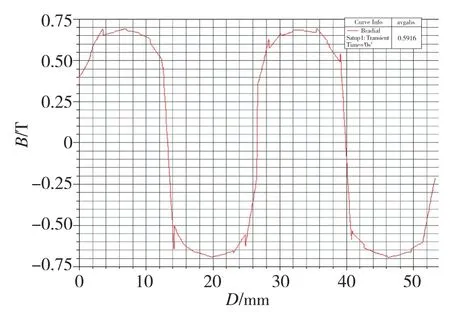
圖7 空載氣隙磁密波形 (內)
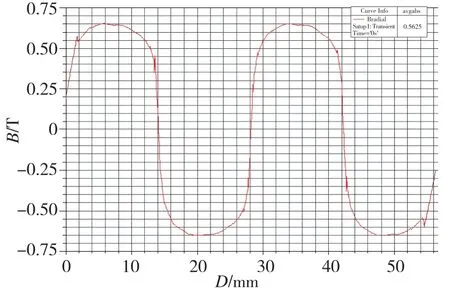
圖8 空載氣隙磁密波形 (外)
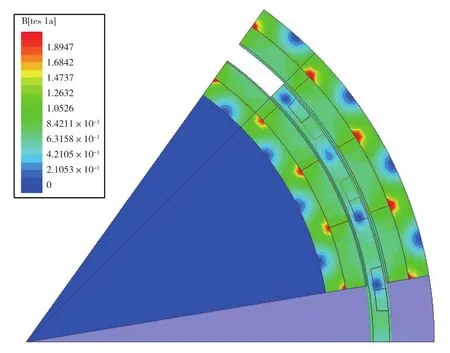
圖9 樣機磁密分布
圖10所示為電機在n=1000r/min時的空載反電勢波形,從圖中可以看出,三相反電勢波形對稱,相反電勢的有效值為11.3V。為了抑制力矩波動,合理優化設計電機尺寸、磁鋼充磁方式,會獲得較平的反電勢波形,以降低力矩波動[9-10]。
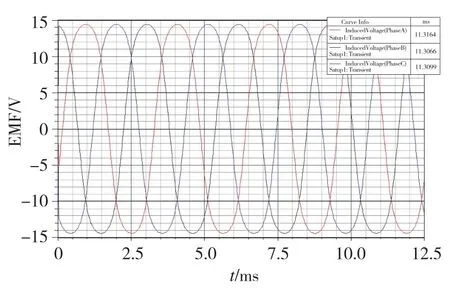
圖10 空載相反電勢波形
2)電機力矩分析
雙磁鋼轉子電機有限元仿真模型為電壓源激勵,通過設置電源供電電壓,可得到負載磁場轉矩的動態波形。通過有限元計算得到電機最大功耗下的力矩波形如圖11所示。
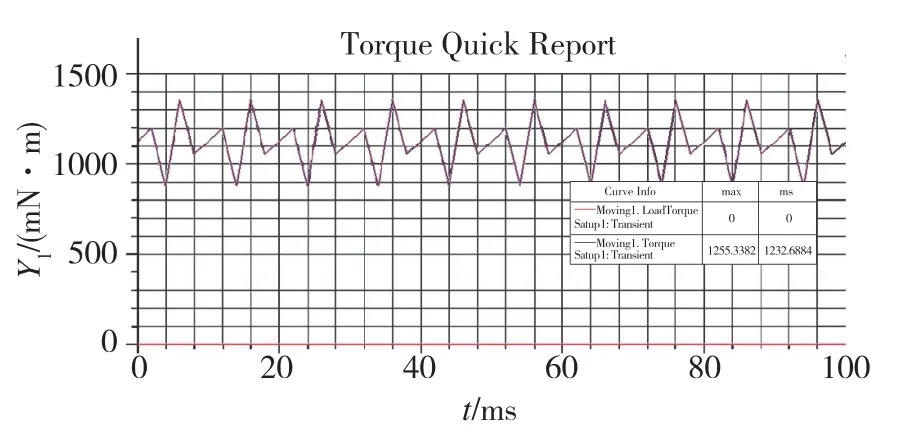
圖11 負載運行時轉矩波形
由圖11可見,電機電磁力矩的有效值為1.2N·m,輸出性能滿足電機技術指標要求,能夠達到運行時的輸出轉矩。
4 結 論
本文針對大力矩飛輪超大力矩輸出的設計要求,采用了一種基于雙磁鋼轉子的永磁電機,可以有效提高氣隙磁密,使氣隙磁密接近0.6T,相對于傳統電機的氣隙磁密一般不超過0.5T,磁負荷有了較大的提升,從而實現了電機整體結構的輕量化。通過有限元仿真計算,驗證了該設計能夠滿足指標要求,實現了大力矩輸出。

