長昆客運專線鐵路路塹邊坡監測數據預處理方法

郭帥杰,宋緒國,隋孝民,莊仲欣,張　磊

(1.中國鐵路設計集團有限公司,天津　300251； 2.城市軌道交通數字化建設與測評技術國家工程實驗室,天津　300251)

1　研究背景

長昆客運專線為滬昆客運專線西段主要組成部分，位于湖南、貴州和云南境內，區段列車最高時速250 km，并預留提速條件。其中，長沙至玉屏區段主要為山地丘陵地貌[1]，部分線路以高路塹邊坡形式通過，線路中心最大挖深27.5 m，最大路塹邊坡高度為42 m。

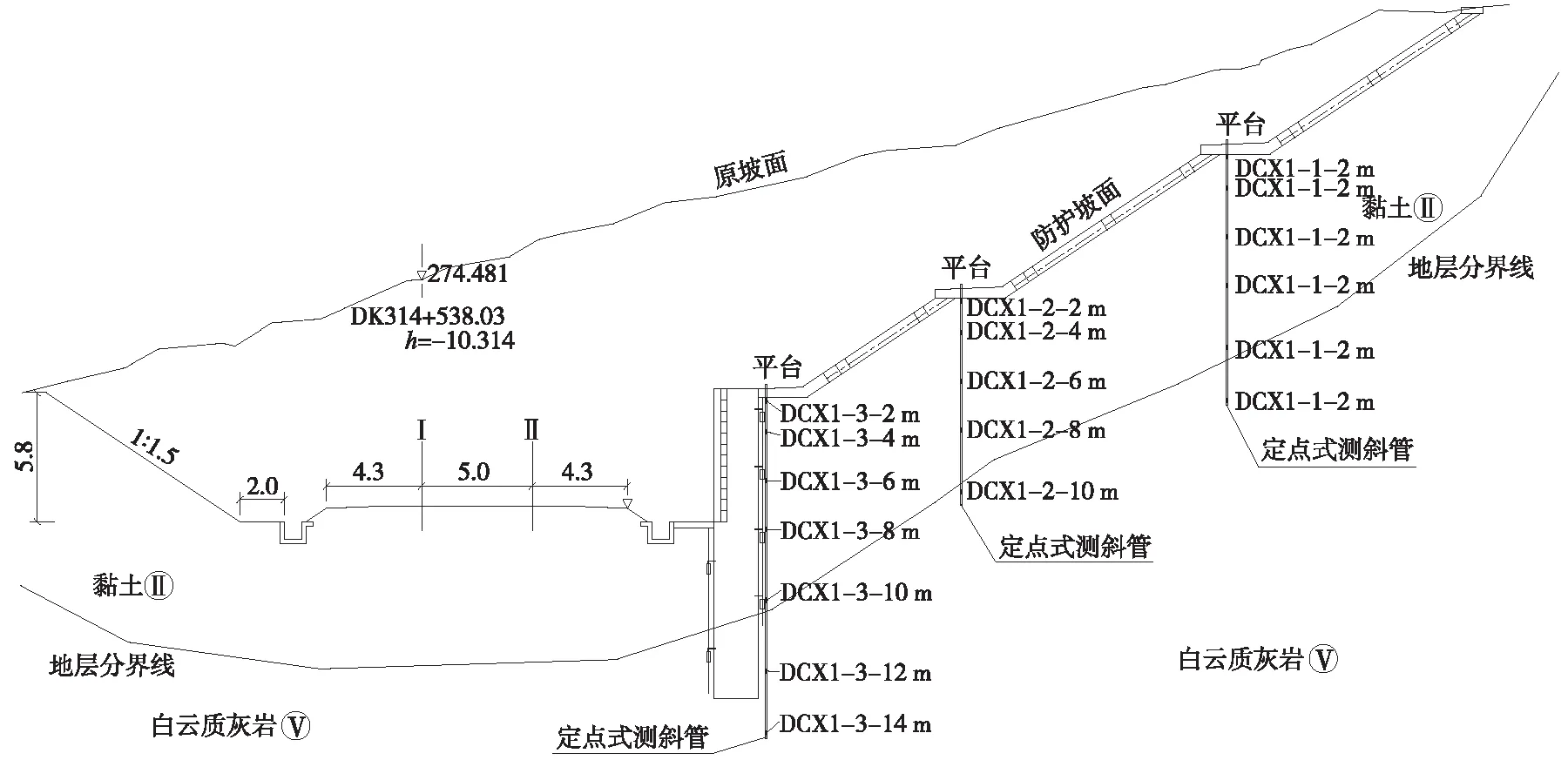
圖1　監測斷面1及定點式水平位移計埋設情況(單位：m)

長昆客運專線長沙至玉屏段現場監測方案設計中，于湖南省懷化市中方縣境內的典型區段設置4個路塹邊坡位移監測斷面(DK314+538、+541、+544、+582)，進行坡面位移、深層水平位移和樁體前后土壓力的自動監測，每天固定時間實時傳輸監測數據。監測結果表明，4個斷面埋設元器件監測數據時程曲線均表現出明顯的跳躍性、無序性特點，既無法預測路塹邊坡位移發展趨勢，也無法判定其穩定狀態，若不進行必要的還原和平滑處理[2-5]，現場實測數據并無實際指導意義。為提高路塹邊坡自動監測數據預警預報和邊坡安全狀態評估能力[6-8]，通過定點式水平位移計監測數據還原和平滑降噪處理，研究路塹邊坡自動化監測數據預處理方法。

2　長昆客運專線路塹邊坡位移監測結果

2.1　工程監測斷面情況概述

長昆客運專線長沙至玉屏段路塹邊坡監測段位于新建鄉特大橋與黃板橋1號大橋間，采用挖方方式通過山包腰部，地形起伏較大，地表植被茂密，植被以灌木和雜草為主，其中，DK314+767～DK316+700區段內存在斷裂。路塹邊坡淺層為弱膨脹性的褐黃色硬塑黏土，層厚2～10 m；深層為巖體較為完整的弱風化、中厚層狀分布的白云質灰巖，巖層產狀131°∠54°，中線走向258.6°，右側順層。區段內巖溶發育等級為中等發育，地下水為第四系孔隙潛水、碳酸鹽裂隙巖溶水和淺變質巖裂隙水，大氣降水補給為主，埋深為4.5～13.5 m。

長沙至玉屏段路塹邊坡現場監測方案設計中，共布設DK314+538(斷面1)、+541(斷面2)、+544(斷面3)、+582(斷面4)4個監測斷面，監測斷面1及定點式水平位移計埋設情況如圖1所示，其他斷面元器件埋設情況與斷面1基本相同。水平位移點編號DCX1-1-2 m表示第1個監測斷面上第1個平臺處距孔口高程為2 m位置處的位移計監測點，監測數據初始接收時間為2013年10月16日。

2.2　平臺水平位移原始監測結果

根據1～4監測斷面臨近坡面位置處的水平位移計原始監測數據，整理得到各監測點位置的原始水平位移時程曲線，如圖2所示。圖2中各監測斷面坡面附近的水平位移測點時程曲線均表現為十分明顯的跳躍性、無序性特點，并不能直接作為邊坡穩定狀態的評估依據。其中，監測時間進入260～400 d區域時，受外部環境或采集儀誤差等因素的影響，各測點水平位移時程曲線均進入強擾動期，說明此階段外界因素出現強烈變化，同時影響4個監測斷面的各位移監測點，此外，對比現場監測的土壓力、坡面位移計監測結果，該時間段內數據亦出現明顯異常，初步判定現場多通道集成數據采集儀出現采集誤差。

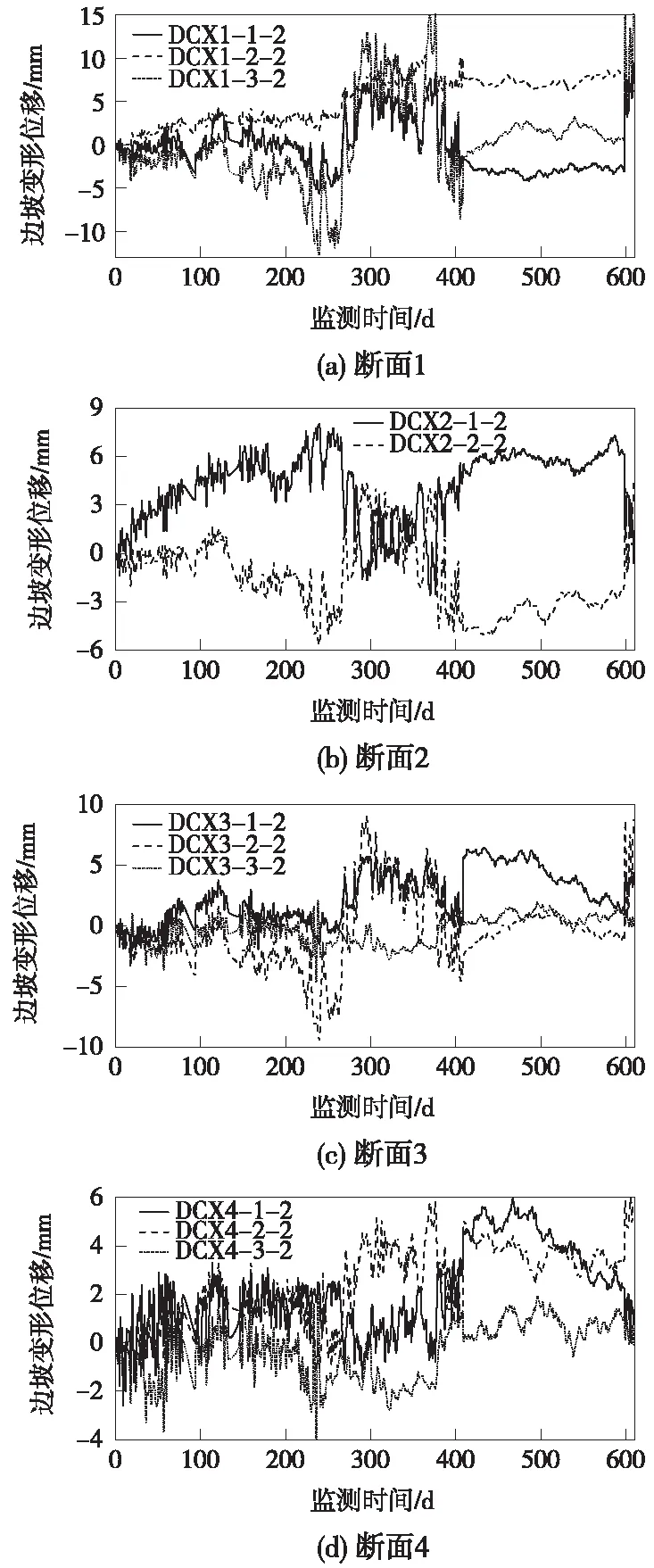
圖2　各斷面水平位移計原始監測曲線

由于各測點水平位移并無明顯變化趨勢，無法進一步預測或評估邊坡穩定狀態，若不進行原始監測數據的預處理[9-10]，監測數據將失去其實時反饋和現場預警意義[11-12]。因此，必須采用一定的平移還原、奇異點剔除還原和平滑降噪處理方法，得到邊坡各測點接近于真實變形狀態的水平位移時程曲線，滿足邊坡位移發展趨勢預測和穩定性評價要求。

3　原始監測數據的平移還原與插值

3.1　監測數據的平移還原

圖2中包含了4個斷面共11個測點的水平位移時程曲線，為簡化分析工作量，本文以DCX1-2-2、DCX2-1-2和DCX4-2-2三個測點為例完成原始監測數據的還原，還原結果如圖3所示。其中，DCX1-2-2測點于260 d和360 d時間位置處于短時間內出現大幅度突變，DCX2-1-2測點于206 d位置處出現突變，分別通過平移方法得到相應還原曲線。DCX4-2-2測點時程曲線整體變形趨勢滿足路塹邊坡的一般規律，但于260 d和400 d附近時間區域出現突變，存在短時間的大量異常數據點，通過異常點剔除方法，得到了接近于路塹邊坡實際變形規律的還原曲線。

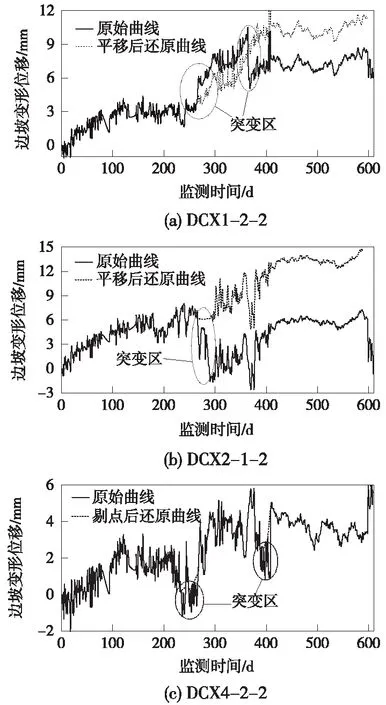
圖3　三測點原始曲線的還原結果

3.2　還原曲線的等時距轉換

圖3中平移或異常點剔除后的還原曲線雖能得到路塹邊坡水平位移總體趨勢，但實際上還原后的數據序列并非等時距，存在因儀器故障或奇異點剔除產生的“漏點”現象。同時，還原后序列時間間隔基本保持為1.0 d，數據量過多，如果將序列時間間隔增大，在保證新序列總體趨勢同還原后序列相似的同時，應用含有較少元素的新序列預測路塹邊坡總體變形趨勢或建立相應的預測分析模型，無疑更具有工程實用價值。

常用的等時距序列轉換方法為插值方法，經典插值方法包括拉格朗日插值，牛頓插值，艾爾米特插值、分段線性插值及樣條插值等[2]。這些方法均具有成熟的理論背景和豐富的工程應用經驗。其中，拉格朗日方法具有結構簡單，適用性廣的優點，在數據點足夠情況下，可實現任意多次的多項式插值。對應的，線性和二次拋物形式的拉格朗日基本插值公式分別如式(1)和式(2)所示。

(1)

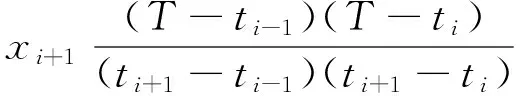
(2)

式中，Xi為線性或二次拋物插值目標函數；(ti-1，xi-1)、(ti，xi)、(ti+1，xi+1)為原始序列數據點，且i>1;T為待插數據點對應的新時間序列。

圖4為原始序列xi轉換為等時距序列Xi的插值過程示意，根據圖示過程，首先確定插值后的等時距序列時間間隔ΔT，其確定方法可預設一合理值，也可取原始時間序列各時間間隔的平均值，或者取原始時間序列的最小公約數。得到等時距序列時間間隔后，由式(3)確定插值后等時距序列的時間序列Ti，并依次賦值給時間T，應用式(1)線性插值或式(2)二次拋物插值得到最終的等時距序列Xi。

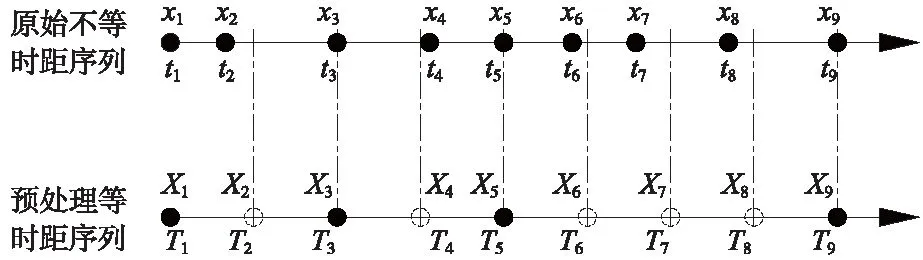
圖4　等時距序列插值示意

式中，Ti為等時距時間序列；ΔT為等時距序列的時間間隔；t1為原始序列的第一個時間數據點。

特別的，應用拉格朗日插值公式進行插值計算中，當插值點附近還原序列相鄰數據點的時間間隔比值小于2.0時，宜采用二次拋物插值方法；否則，應采用線性插值方法進行等時距序列轉換。

通過上述方式，對圖3中DCX1-2-2、DCX2-1-2和DCX4-2-2測點水平位移還原曲線進行等時距處理轉換，得到包含由50個數據點組成的等時距序列，轉換后等時距序列時間間隔約為13.2 d，各測點對應的等時距序列曲線如圖5所示。

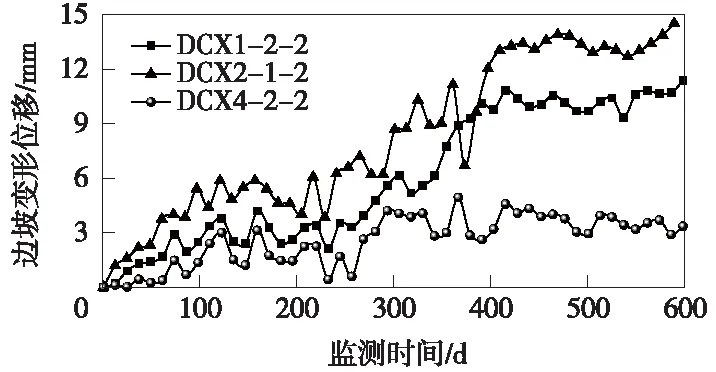
圖5　三測點等時距序列曲線

對比圖3(a)(b)(c)中三測點的還原曲線，包含50個數據點的圖5等時距序列曲線能夠反映出三測點水平位移時程曲線的變化趨勢。400 d時間范圍內，路塹邊坡水平位移時程曲線基本保持線性增加趨勢，但超過400 d后，路塹邊坡變形趨于穩定。

此外，圖5中插值后的等時距序列曲線中間數據仍表現出較強的波動性和隨機性特點，研究中采用平滑降噪方法進一步處理，得到更為真實的路塹邊坡位移變形趨勢，以滿足后續的位移預測模型建模和路塹邊坡穩定性分析。

4　數據序列平滑與平滑效果評價

4.1　平滑降噪方法

一般情況下，邊坡位移監測位移時程曲線大多呈現出明顯的隨機波動性特點，而其原因主要有兩個方面，一是自然因素(降雨、地震、地下水變化等)和人為因素(施工、爆破、車輛振動等)等外部因素引起的，二是監測儀器本身由于磁場干涉、電壓失穩等因素引起的監測信號周期性波動現象。而在位移發展趨勢判定及位移發展預測模型建立中，應盡量去除隨機性因素影響。因此，采用降噪方法對監測數據進行合理平滑去噪處理，保證降噪后數據不僅有效去除數據中的隨機噪聲數據部分，并且保留反映邊坡總體變形趨勢的有效數據信息。

目前，波動數據降噪處理已有多種方法，其中較為廣泛使用的是最小二乘多項式平滑方法、傅里葉變換平滑、分箱技術及小波變換去噪技術等[2]。考慮到各方法實際工程應用效果和推廣意義，本文在路塹邊坡位移監測數據平滑降噪處理中采用最小二乘多項式平滑降噪方法，通過相對簡單有效的途徑，實現對邊坡位移原始監測數據的高效快速處理。

設一組含噪聲數據序列為X1，X2，…，Xn,,對應時間節點序列為T1，T2，…，Tn，應用m次多項式擬合數據，其擬合表達式為

Y(T)=A0+A1T+A2T2+…+AmTm

(4)

應用最小二乘法確定式(4)中方程待定系數，得到擬合關系式和目標數據間方差表達式(5)。

(5)

最小二乘法求解應使式(5)數值最小，分別對Xi(i=0，1，…，m)求偏導，并令各偏導數方程為0，得到式(6)形式的正規方程組。

(6)

由式(6)依次解得擬合方程系數A1，A2，…，Am。等時距序列平滑過程中，若平滑窗口采用五點數據格式，令時間序列為1，2，3，4，5，分別得到式(7)二次拋物線和式(8)三次拋物線五點平滑公式，式中，i=3，4，…，n-2。

(7)

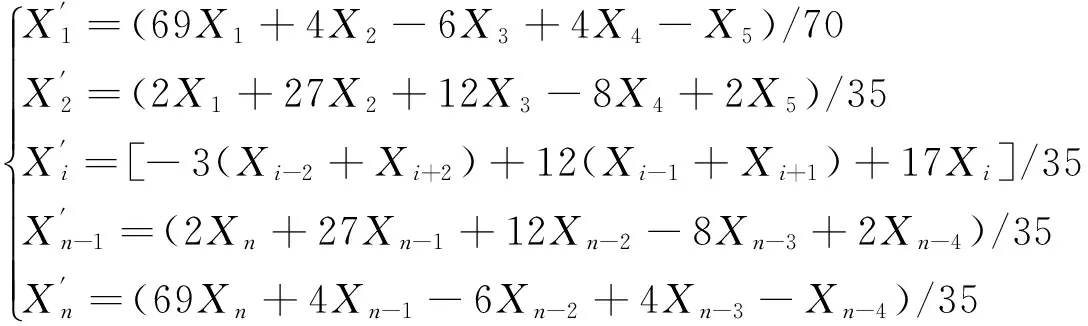
(8)

此外，應用比較多的還有三點平滑法，其實際上是一種取算術平均值的數學方法。考慮到邊坡監測位移序列數據點較多，本文選用三次拋物線平滑方法進行插值完成后等時距位移序列的降噪處理。

平滑效果主要有均方根誤差RMSE、信噪比SNR和平滑度指標r。各平滑效果指標表達式依次為式(9)、式(10)和式(11)形式。

(9)

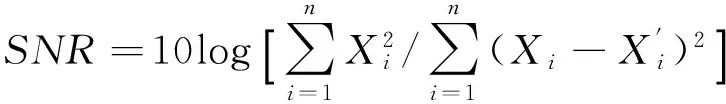
(10)

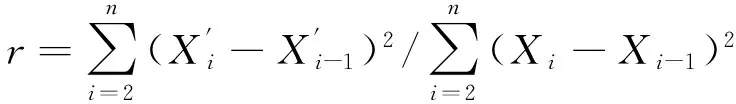
(11)

均方根誤差RMSE體現了原始數據與去噪后數據間的差異，均方差越小，表示去噪結果越接近原始序列；信噪比SNR是原始數據能量和噪聲數據能量的比值，信噪比越大，降噪后序列同原始序列越接近，噪聲水平越低；平滑度指標r反映出降噪后序列的相對平滑性能，平滑度指標越小，去噪效果越好。

4.2　斷面測點水平位移還原曲線的降噪處理

數據序列降噪效果主要同循環次數相關，循環次數越多，降噪后的平滑序列噪聲水平相對越低，平滑性也越好，但與原始序列間差異也越大。因此，原始監測數據平滑降噪處理過程中，應合理控制平滑循環次數，在保證處理后數列平滑度的基礎上，保證降噪后數據不至于失真。

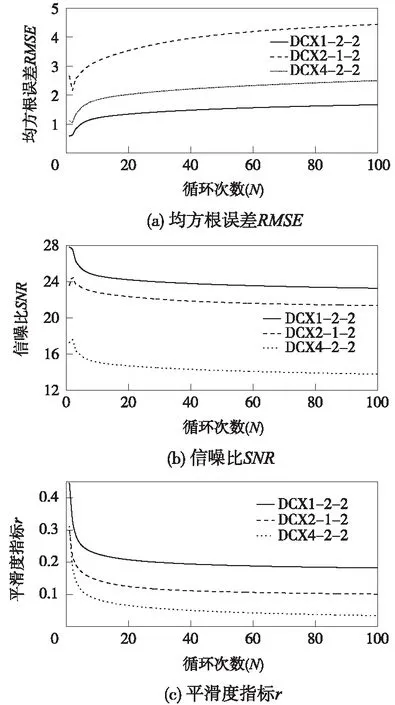
圖6　降噪效果評價指標同循環次數間關系曲線

對包含50個數據點的DCX1-2-2、DCX2-1-2和DCX4-2-2測點等時距序列平滑降噪處理，得到不同循環次數下的均方根誤差RMSE、信噪比SNR和平滑度指標r同循環次數N之間的關系曲線，如圖6所示。從圖6可看出，含噪序列平滑過程中，均方根誤差RMSE、信噪比SNR、平滑度指標r分別隨循環次數N的增加而升高、降低和降低，即降噪循環次數越多，平滑后數據序列同原始序列間差異越大，降噪后的序列噪聲水平越低，序列平滑性越好。但同時，平滑后序列相較于原序列可能存在數據失真現象，故降噪循環次數并非越多越好。

圖6中，當循環次數較小時，3種降噪效果評價指標均隨循環次數的增加出現大幅變化，但當循環次數超過一定次數后，3種降噪效果評價指標的變化趨勢漸緩，且總體變化幅度很小。因此，可將各降噪評價指標隨降噪循環次數的變化曲線中曲率最大點后的某一循環次數作為合理值，在滿足含噪數據降噪效果的同時，保證降噪后數據序列能夠反映原始序列趨勢的真實性。

對比圖6(a)(b)(c)中均方根誤差RMSE、信噪比SNR和平滑度指標r趨勢線，當循環次數達到10次時，各趨勢線曲率最大，序列降噪效果最為明顯；循環次數達到20次時，基本可保證降噪后序列的各評價指標趨穩。因此，路塹邊坡監測數據降噪處理采用五點三次拋物方程降噪中，統一進行20次左右的降噪循環，滿足降噪后路塹邊坡監測數據的平滑性和真實性。圖7為經過20次循環平滑降噪后，DCX1-2-2、DCX2-1-2和DCX4-2-2測點平滑降噪后的序列曲線，三測點降噪后曲線隨機性數據點明顯減少，平滑序列平順度顯著提高。

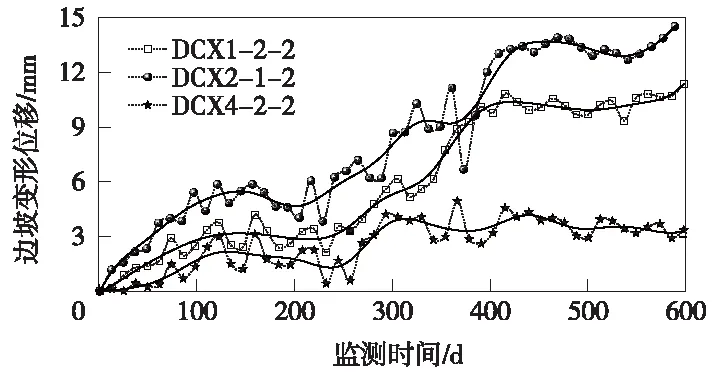
圖7　20次循環后的三測點位移平滑降噪曲線

4.3　斷面測點位移數據序列擬合方程

路塹邊坡變形監測目的是進行邊坡災害預警和變形發展趨勢預測，預警指標一般采用位移變形極限值或變形速率極限值，而變形趨勢預測則需要根據路塹邊坡監測位移時程曲線[13-15]。因此，20次平滑降噪處理后的邊坡位移監測數據平滑曲線可通過多項式擬合方法，獲得位移監測數據的擬合曲線，并進行邊坡位移發展趨勢的短期預測。

根據圖7中DCX1-2-2、DCX2-1-2和DCX4-2-2三測點水平位移監測數據平滑降噪后的數據序列曲線，通過六次多項式擬合方法，分別得到圖8中3個監測點平滑降噪后水平位移曲線的多項式擬合曲線。從圖8可以看出，六次函數擬合曲線能夠準確反映各測點水平位移隨時間的變化趨勢，說明應用高次多項式函數進行路塹邊坡監測數據模擬是可行的。但必須說明的是，高次多項式函數并不能很好反映未來時間段內的數據序列變化趨勢，僅能滿足路塹邊坡位移變形的短期預測，如果進行中長期預測則極可能產生較大預測誤差。具體工程應用中，首先根據實測數據進行平移還原，平滑降噪處理后得到測點監測數據的還原曲線，并應用高次多項式函數擬合，最后進行未來短時間內的位移變形趨勢和變形量預測。

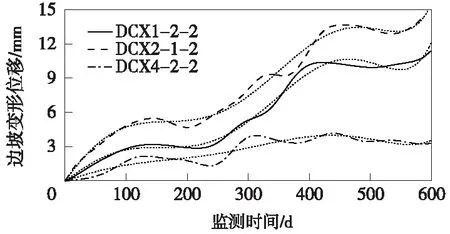
圖8　三測點位移多項式擬合曲線

式(12)為對應的六次多項式擬合方程式。表1為3個測點位移曲線的六次多項式擬合方程的各項系數列表，3個監測點高次函數擬合方程的相關系數均超過0.999 9，這也說明六次多項式函數擬合方法對已測位移變形數據具有較好擬合效果。

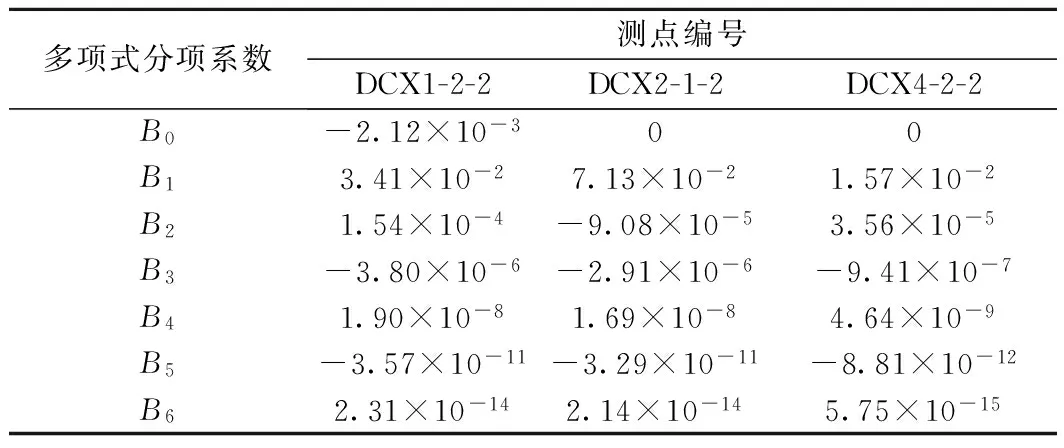
表1　試驗段計算參數

X(t)=B0+B1t+B2t2+B3t3+B4t4+B5t5+B6t6

(12)

式中，X(t)為測點擬合位移；t為監測時間；B0～B6為六次多項式分項系數。

5　結論

路塹邊坡位移監測直接反應開挖和運營過程中的邊坡穩定狀態和變形發展趨勢，但由于眾多因素的干擾影響，監測數據往往表現出較強的波動性和隨機性，并不能代表邊坡監測位移發展趨勢，難以直接應用。研究中以長昆客運專線長沙至玉屏段部分路塹邊坡水平位移監測結果為基礎，開展原始監測數據的還原方法、等時距轉換方法、平滑降噪方法和多項式擬合方法的研究，并得到以下結論。

(1)受制于現場諸多因素，路塹邊坡自動監測數據時程曲線存在突變和波動現象，監測數據預處理中應根據曲線特點，采用平移或異常點剔除方法還原真實監測數據。

(2)測點監測數據序列等時距轉換中，可采用線性插值或二次多項式插值，但當插值點附近相鄰時間間隔比值超過2.0倍時，宜采用線性插值。

(3)還原后數據序列的平滑性隨平滑循環次數逐漸增加，數據所含噪聲水平逐漸降低；應用三次拋物線平滑方法循環降噪20次時，即可滿足平滑降噪要求。

(4)平滑降噪后的等時距序列可應用高次函數多項式擬合，并能滿足短期預測要求，但中長期預測效果較差，擬合數據范圍應實時更新。

(5)該研究成果可為鐵路工程路塹邊坡自動監測數據的預處理方法提供參考和借鑒。

參考文獻：

[1]唐元峰.長昆客運專線高瓦斯煤層地區隧址綜合比選[J].高速鐵路技術，2011(S1):357-361.

[2]蔚清.邊坡監測數據預處理方法比較及建模研究[D].合肥：合肥工業大學，2013.

[3]張松，田林亞.時間序列分析在地鐵沉降監測中的應用[J].測繪工程，2014，23(10)：63-66.

[4]陳善雄，余飛，劉紹波，等.鐵路客運專線沉降監測數據管理與分析預測集成系統研發[J].鐵道標準設計，2010(2)：31-36.

[5]鄭懷洲.北京地鐵東四站地表沉降監測數據分析[J].鐵道標準設計，2006(4)：60-62.

[6]劉漢東，阮飛鵬，李國維.粵贛高速公路k2邊坡監測與穩定性研究[J].巖土力學，2008，29(12)：3365-3369.

[7]宋章，王科，崔建宏，等.路塹邊坡滑坡成因機制淺析及防治對策[J].鐵道工程學報，2015(4)：27-31.

[8]史丹.深部位移監測在東西高速滑坡處治中的應用[J].鐵道工程學報，2012(9)：39-44.

[9]譚捍華.基于綜合監測信息的類土質邊坡動態施工影響分析[J].公路交通科技，2011，28(6)：40-46.

[10] 夏元友，劉鵬，莫介臻.高速公路軟基沉降預測系統及其應用研究[J].公路，2008(8)：275-279.

[11] 蔣楚生.高標準鐵路路塹邊坡設計中常見問題的探討[J].鐵道工程學報，2012(2)：32-36.

[12] 林燦陽，魏土榮.邊坡深孔監測位移曲線異常的原因分析及糾正措施[J].路基工程，2014(5)：175-180.

[13] 陳曉鵬，張強勇，劉大文，等.邊坡變形統計回歸分析模型及應用[J].巖石力學與工程學報，2008，27(S2)：3673-3679.

[14] 徐衛東，伍錫銹，歐海平.附有等式約束的Kalman濾波方法及其在邊坡監測中的應用[J].測繪工程，2013，22(2)：61-63.

[15] 馬玉梅.多元回歸分析方法在高層建筑沉降監測數據處理中的應用[J].測繪與空間地理信息，2016，39(12)：183-185.