基于自適應鄰域空間粗糙集模型的直覺模糊熵特征選擇

姚 晟 徐 風 趙 鵬 紀 霞

(計算智能與信號處理教育部重點實驗室(安徽大學) 合肥 230601) (安徽大學計算機科學與技術學院 合肥 230601) (fisheryao@126.com)

隨著計算機和互聯網的迅速發展，數據急劇增加.然而，現實中的很多數據包含著大量的冗余特征(又稱為屬性)，這些特征不僅降低了數據的分類性能，而且還增加了計算的復雜程度，因此需要對它們進行消除.特征選擇(又稱為屬性約簡)是數據預處理中很重要的一項技術，其基本思想是在沒有降低數據分類精度的情形下盡可能去消除那些冗余的特征，最終得到一個特征子集.近年來，特征選擇方法廣泛地運用于機器學習、模式識別和數據挖掘等領域中[1-3].

特征評估是特征選擇方法中一個很關鍵的環節，如何構建一個有效的評估函數一直是特征選擇研究的重點.目前，學者們提出了很多關于特征評估的方法，如信息熵[4-5]、依賴度[6]和相關性[7]等.基于不同評估方法得到的特征選擇結果也可能不同.

粗糙集理論是波蘭學者Pawlak[8]提出的一種處理模糊和不確定性知識的方法,目前已被廣泛運用于特征選擇方法中[4,6,9].傳統的粗糙集理論建立在等價關系的基礎上，把依賴度作為屬性的評估依據.這種方法只適用于符號型屬性的評估，由于現實中很多數據是連續型的，因此基于傳統粗糙集理論的特征選擇方法具有一定的局限性.Lin[10-11]運用鄰域關系代替等價關系，提出鄰域粗糙集模型，這種模型可以直接處理連續型屬性，放寬了粗糙集理論的適用范圍.同時，基于鄰域粗糙集模型的特征選擇算法也相繼提出[6,9,12].

目前，基于鄰域粗糙集模型的特征選擇算法中，利用鄰域關系刻畫對象之間的相似性[10]進行特征評估，并通過鄰域半徑來限定對象的鄰域，這種方式雖然可以直接處理連續型數據，但是也存在一些問題.由于現實中很多的數據集是海量高維的，且有些數據可能是分布式的，因此這可能導致不同特征下的數據分布不均，甚至同一特征下不同類別的數據分散程度也不一樣，而傳統的鄰域粗糙集模型只是通過距離函數和鄰域半徑來構造鄰域關系，這樣會產生許多誤分類現象，從而影響到最終特征選擇的結[6,12].Min[13]等學者提出誤差范圍的覆蓋粗糙集模型，在這個模型中利用一個誤差范圍來修正對象的鄰域，并同時提出了相應的特征選擇算法.Zhao[14]等學者在假設這個誤差滿足高斯分布的情形，提出了自適應鄰域粒模型，并提出基于該模型的特征選擇算法.可以看出關于鄰域誤差的問題，目前越來越受到研究人員的關注.

本文針對目前鄰域粗糙集模型存在的不足，引入二元鄰域空間理論的定義[15]，用方差刻畫數據的分布情況，依據方差將鄰域半徑分配到各個屬性下，使每個屬性對應的鄰域半徑能夠自適應數據的分布狀況，利用這種方法我們定義了自適應二元鄰域空間理論，同時提出了對應的粗糙集模型.隨后再結合鄰域直覺模糊熵[16]來構造評估函數，并給出相應的特征選擇算法.在實驗分析中，我們分別將提出的算法和目前已有的特征選擇算法進行實驗對比，最終結果表明本文提出的特征選擇算法具有更好的性能.

1 基本理論

1.1 經典粗糙集模型

定義1[8]. 信息系統.設信息系統IS=(U,AT,V,f)，?B?AT，由屬性子集B誘導的等價關系IND(RB)定義為

IND(RB)={(x,y)∈U×U|a(x)=a(y),?a∈B}，

等價關系IND(RB)滿足對稱性、自反性和傳遞性.由IND(RB)誘導出的劃分表示為UIND(RB),其中包含對象x的等價類[x]B定義為

[x]B={y∈U|(x,y)∈IND(RB)}.

定義2[8]. 近似集.設信息系統IS=(U,AT,V,f)，B?AT，?X?U關于B的下近似和上近似分別定義為

另外?X?U關于B的正區域、負區域和邊界域分別定義為

1.2 二元鄰域空間

經典粗糙集理論是建立在等價關系的基礎上，因此只適用于符號型屬性，而無法處理連續型屬性.Lin[10-11,15]通過引入鄰域的概念，將粗糙集理論推廣到鄰域空間，鄰域空間可以直接處理數值型屬性.本節我們主要介紹二元鄰域空間[15]的基本內容.

定義3[10]. 鄰域.設鄰域信息系統NIS=(U,AT,V,f)，其中U為有限對象集，AT為屬性集且均為連續型，V為屬性的值域，f為函數映射：U×AT→V.?x∈U關于屬性集B?AT的δ鄰域定義為

其中,δ稱為鄰域半徑，是一個非負常數;ΔB(x,y)被稱為對象x和y之間的距離.常用的距離公式為閔可夫斯基距離，設屬性集B={a1,a2,…,am}，閔可夫斯基距離定義為

閔可夫斯基距離有3種常用的形式:

1) 當P=1時，

此距離又稱為 Manhattan距離;

2) 當P=2時，

此距離又稱為Euclidean距離;

3) 當P=∞時，

此距離又稱為Chebychev距離.

定義4[15]. 鄰域系統.對于鄰域信息系統NIS=(U,AT,V,f)，A?AT,設B1,B2,…,Bm?A，稱β={RBi|1≤i≤m}為二元鄰域關系集，這里滿足RBi={(x,y)|ΔBi(x,y)≤δBi}.那么?x∈U基于β中二元鄰域關系RBi(1≤i≤m)的鄰域定義為nBi(x)={y∈U|(x,y)∈RBi}，對象x在β下的所有鄰域的集合NSB(x)稱為對象x的鄰域系統，即NSB(x)={nBi(x)|1≤i≤m}，并且稱{NSB(x)|x∈U}為U上的鄰域系統，用NSB(U)表示.那么(U,β)稱為二元粒計算模型；(U,NS(U))稱為β上的二元鄰域空間，簡稱鄰域空間.

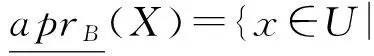
同樣地，X關于鄰域空間(U,NSB(U))的正區域、負區域和邊界域分別定義為

可以看出，鄰域空間的下近似、上近似和邊界將論域U劃分成3個區域.

2 自適應二元鄰域空間

設鄰域信息系統NIS=(U,AT,V,f)，在B?AT誘導的二元鄰域空間(U,NSB(U))中，對象x∈U的鄰域系統NSB(x)由x的鄰域構成，通常鄰域空間中的距離函數大多選取閔可夫斯基距離，對于對象x，如果?y∈U與x的距離不超過給定的鄰域半徑δ，那么y將被包含在x的鄰域中，這樣卻存在一定缺陷.設屬性集C={a1,a2,…am}，對于對象x,y∈U，因此閔可夫斯基距離定義為

可以看出，對象x,y在屬性集C下的距離是由各屬性下距離分量|ai(x)-ai(y)|p的共同結果.實際上，數據集的每個屬性表示的是不同的指標，這些屬性下取值的分布情況可能會不同，有的屬性值比較集中，有的屬性值就比較發散，甚至對于同一個屬性，不同類別下數據的分布情況也不一樣.正是由于這種因素，使得對象之間在各屬性下的距離占總距離的比重不一樣，如果統一設定一個鄰域半徑，導致聚集程度較大的屬性對最終總距離的貢獻較小，使得對象之間距離主要取決于發散程度較大的數據，這顯然是不合理的，同時構造的鄰域存在著一定誤分類情形.具體情形可以觀察例1.

例1. 表1所示的是一個鄰域決策信息系統NIS=(U,AT∪g0gggggg,V,f)，AT={a1,a2,a3}.

Table 1 Neighborhood Decision Information System表1 鄰域決策信息系統

我們設B={a1,a2}，分別計算δ=0.05和δ=0.1下每個對象的鄰域：

當δ=0.05時，

nB(x1)={x1,x3}，
nB(x2)={x2,x3}，
nB(x3)={x1,x2,x3}，
nB(x4)={x4}，
nB(x5)={x5}，
nB(x6)={x6}.

當δ=0.1時，

nB(x1)={x1,x2,x3}，
nB(x2)={x1,x2,x3,x6}，
nB(x3)={x1,x2,x3,x6}，
nB(x4)={x4,x5,x6}，
nB(x5)={x4,x5},
nB(x6)={x2,x3,x4,x6}.

觀察表1可以發現，屬性a1和a3的數據較為分散，而屬性a2的數據較為聚集，這使得在計算的結果中，當鄰域半徑取值較小時，每個對象刻畫的鄰域類較為精細，但是在鄰域粗糙集中，較細的鄰域類往往是不能選擇出最優特征子集[6,12].而當鄰域半徑取值較大時，很多的鄰域類中出現了誤包含現象，即鄰域類中出現了不屬于同一個類的對象，如對象x2，x3，x6的鄰域類.同樣，這樣也不能選擇出最優的特征子集[6,12].

為了解決以上存在的問題，本文定義一種自適應鄰域空間(U,aNS(U))，其中對象x∈U的自適應鄰域系統表示為aNSB(x).自適應鄰域空間的主要思想是對于一個給定的鄰域半徑，我們按照數據的方差將鄰域半徑分割到每個屬性下，然后對象按照每個屬性下的對應鄰域半徑求取鄰域，最終的自適應鄰域系統aNSB(x)由對象x在每個屬性下的鄰域構成.

定義6. 自適應鄰域系統.設鄰域決策信息系統為NIS=(U,AT∪g0gggggg,V,f)，B?AT，給定B下的鄰域半徑為δ，?ai∈B(1≤i≤|B|),x∈U有集合：

VarB(Dx)={Vara1(Dx),Vara2(Dx),…,Vara|B|(Dx)}，

其中,Dx={D∈Ug0gggggg|x∈D}(即包含對象x的決策類),Varai(Dx)表示Dx中各對象在屬性ai下取值的方差.我們定義由B誘導出的對象x的自適應鄰域系統為

定義7. 自適應近似集.設鄰域信息系統NIS=(U,AT,V,f)，B?AT，并且B下的鄰域半徑為δ，?X?U關于自適應鄰域空間(U,aNSB(U))的下近似和上近似分別定義為

此外，X關于自適應鄰域空間(U,aNSB(U))的正區域、負區域和邊界域分別定義為

證畢.

證畢.

3 鄰域直覺模糊熵

直覺模糊集是由Atanassov[17]在模糊集理論的基礎上進行的推廣.直覺模糊集理論中，首先分別定義一對關于對象的粗糙直覺隸屬度函數，即隸屬度μ(x)和非隸屬度ν(x)，然后在這2個函數的基礎上進一步定義了猶豫度函數π(x)=1-μ(x)-ν(x)，利用這3個函數，直覺模糊集的熵理論可以很好地運用于數據的不確定性分析[18-20].我們在Zheng等人[16]的基礎上，定義了自適應二元鄰域空間粗糙集模型中的隸屬度μ(x)和非隸屬度ν(x)函數.

性質3. 設鄰域信息系統NIS=(U,AT,V,f)，B?AT，?X?U,對于x∈U滿足：

證明. 根據定義8可以直接得到.

證畢.

信息熵作為信息系統中一種重要的不確定性度量方法，學者們對它作了大量的研究[4,21-22].近年來，學者們將模糊熵和直覺模糊熵運用于信息系統的不確定性度量，取得了很多不錯的成果[16,23].接下來，我們在Zheng等人[16]提出的鄰域直覺模糊熵的基礎上結合自適應鄰域空間，提出基于自適應鄰域空間粗糙集的鄰域直覺模糊熵.

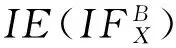
這里的

其中

特別地，對于鄰域決策信息系統NIS=(U,AT∪g0gggggg,V,f)，Ud關于B的直覺模糊熵IE(I)定義為

其中,Ud={D1,D2,…,Dm}.

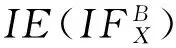
證明. 首先，我們分析一下函數

證畢.

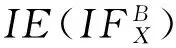
綜上所述，有:

證畢.

例2. 繼續例1，設鄰域決策信息系統NIS=(U,AT∪g0gggggg,V,f)如表1所示，設B3={a1}，B2={a1,a2}，B1={a1,a2,a3}，這里我們可以得到Ud關于B1，B2，B3的鄰域直覺模糊熵.

Ug0gggggg={D1,D2},其中D1={x1,x2,x3}，D2={x4,x5,x6}.那么：

從性質5可以看出，隨著屬性子集的增加，其鄰域直覺模糊熵的值單調不增，這是一個很重要的性質，它為我們構造基于鄰域直覺模糊熵的特征選擇算法提供了理論依據.

4 特征選擇算法

特征選擇作為粗糙集理論的一個重要的應用，許多研究人員在這方面作了深入的研究[4,6,9]，尤其在鄰域粗糙集模型中，目前已有多種特征選擇算法，例如基于屬性依賴度的特征選擇算法[6]、基于鄰域熵的特征選擇算法[24]、基于模糊集的特征選擇算法[5,25].

由于在直覺模糊集中，對象與集合之間的關系通過隸屬度、非隸屬度和猶豫度3個方面來描述，這3個方面表現出了對象對集合的支持、反對和中立3個觀點，它進一步增強了模糊集的表示能力，處理模糊性具有更多的優勢[17].同時文獻[16]指出了直覺模糊熵具有更好的信息系統不確定性度量效果.因此我們將自適應二元鄰域空間粗糙集模型融合鄰域直覺模糊熵來構造相應的特征選擇算法.

定義11. 屬性重要度.設鄰域決策信息系統NIS=(U,AT∪g0gggggg,V,f)，B?AT，?a∈B，定義a在B下基于決策屬性d的重要度為

在本文提出的特征選擇算法中，我們把定義11中的屬性重要度作為特征評估函數.其算法的具體構造過程如下所述.

對于鄰域決策信息系統NIS=(U,AT∪g0gggggg,V,f)，為了降低算法的時間復雜度，根據定義6，我們首先計算出AT中每個屬性下各個決策類的方差.

算法1. 計算方差VarB(Di)(Di∈Ug0gggggg)和VarB.

輸入：NIS=(U,AT∪g0gggggg,V,f)，AT={a1,a2,…,a|AT|}；

輸出：方差VarAT.

Step1. 計算決策屬性d的劃分Ug0gggggg={D1,D2,…,Dm}.

Step2. 對于Ug0gggggg中每個決策類Di，計算在所有條件屬性下的方差，即屬性集AT下Di的方差表示為

VarAT(Di)={Vara1(Di),Vara2(Di),…,Vara|AT|(Di)}.

Step3. 由Step2的結果可以得到：

VarAT={VarAT(D1),VarAT(D2),…,VarAT(Dm)}.

設|U|=n，|AT|=c，那么算法1的時間復雜度為O((c+1)n).

我們計算U上的自適應鄰域系統aNSB(U)，即計算?x∈U的aNSB(x)，其中B?AT，具體過程如算法2所示.

算法2. 計算aNSB(U).

輸入：NIS=(U,AT∪g0gggggg,V,f)、B?AT且B={a1,a2,…,a|B|}、鄰域半徑δ、VarAT；

輸出：aNSB(U).

Step3. 根據Step2得到

aNSB(U)={aNSB(x1),aNSB(x2),…,
aNSB(x|U|)}.

這里的

算法2中，設|U|=n，|Ug0gggggg|=m，則Step1的時間復雜度為O(m×|B|)，由于Step2采用文獻[26]提出的排序方法計算鄰域，使得時間復雜度為O(n×lbn)，那么Step2的時間復雜度為O(|B|×n×lbn)，因而算法2的時間復雜度為O(|B|×(m+n×lbn)).

通過算法2求得aNSB(U)，那么就可以計算出自適應鄰域直覺模糊熵，具體如算法3所示.

輸入：NIS=(U,AT∪g0gggggg,V,f)、B?AT且B={a1,a2,…,a|B|}，鄰域半徑δ、VarAT；

Step1. 根據算法2得到aNSB(U).

Step2. 對于決策類Di∈Ug0gggggg：

Step4.返回最終結果

算法3中，|U|=n，|Ug0gggggg|=m，在算法2的結果上，Step2時間復雜度為O(|B|×n)，則Step2至Step3的時間復雜度為O(|B|×mn)，由于Step1的時間復雜度為算法2的時間復雜度，所以整個算法3的時間復雜度為O(|B|×mn+|B|×(m+n×lbn)).

下面構造出本文所提出的特征選擇算法，其基本思想是:利用鄰域直覺模糊熵來評價屬性的重要度，然后每次在剩余的屬性中選擇屬性重要度最大的屬性加入約簡集合中，直到最后滿足算法的終止條件后終止算法，此時約簡集合即為最終的特征選擇結果.具體流程如算法4所示.

算法4. 基于鄰域直覺模糊熵的特征選擇算法(feature selection based on neighborhood intuitionistic fuzzy entropy, FSNIFE).

輸入：NIS=(U,AT∪g0gggggg,V,f)、鄰域半徑δ、終止閾值λ=0.001；

輸出：約簡集合red.

Step2. 計算VarAT.*根據算法1*

Step3. 對于屬性?ai∈AT-red:

Step3.2. 選擇Step3.1中屬性重要度最大的屬性，記為at,將屬性at加入red中.

Step4. 重復進行Step3，直到滿足SIG(at,red,D)≤λ或red=AT時停止.

Step5. 返回結果red.

設|U|=n，|AT|=c，|Ug0gggggg|=m，在算法4中，假設最終的特征選擇的結果為l個屬性，那么Step4的時間復雜度為

因此整個算法的時間復雜度為

即:

當l=c時，此時算法的計算次數最多，因此最壞的時間復雜度為

通常情況下，m?n，因此本文所提出的特征選擇算法的時間復雜度不超過O(c3×n×lbn).

5 實驗分析

為了驗證本文所提的特征選擇算法的有效性，我們首先選取目前已有的3個特征選擇算法[5,12,25];然后將它們和本文提出的特征選擇算法分別對同一數據集進行實驗;最后通過對比各個算法的實驗結果來評估算法的性能，其中性能的評估分別通過特征選擇的數量、算法運行的時間和特征子集的分類精度3個指標體現.

5.1 實驗準備

本文從UCI數據庫獲取了8個數據集，具體信息如表2所示.選擇已有的特征選擇算法分別為：基于信息熵的一種新的模糊粗糙集特征選擇(feature selection based on information entropy of fuzzy rough set, FSFRSIE)算法[5]、基于模糊粗糙集的特征選擇(feature selection based on fuzzy rough set, FSFRS)算法[25]和基于模糊鄰域粗糙集的特征選擇(feature selection based on fuzzy neighborhood rough set, FSFNRS)算法[12].這些算法可以直接運用于連續型屬性，同時為了消除屬性量綱的影響，我們需要將數據進行標準化，但是為了保證數據的方差相對不變，我們這里采用極差正規化變換，變換公式為x*=(x-xmin)(xmax-xmin)，變換后的數據全部位于[0,1]之間.

本實驗所有算法運行的硬件環境為Intel?CoreTMi3 CPU 550,3.2 GHz 和2.0 GB RAM的PC機上，操作系統為Windows 7,實驗所采用的編譯工具為Java.分類精度的計算采用支持向量機(support vector machine, SVM)和決策樹(decision tree, DT)這2種分類器.

Table 2 UCI Data Set表2 UCI數據集

由于鄰域半徑δ的取值對特征選擇的結果具有很重要的影響，因此在本文的算法(FSNIFE)開始計算之前，我們需要確定δ的參數.為了能選擇出合適的特征子集，我們首先將δ在某個鄰域半徑區間上依次選取等步長的值進行實驗，由于每個數據集的特征數目不一樣，鄰域半徑區間的選取也不一樣.初步實驗后我們得到，yeast，wine，mess數據集的區間選取為[0.01,0.3],步長為0.01;wdbc，iono，biodeg數據集的區間選取為[0.01,0.5],步長為0.01;sonar數據集的區間選取為[0.01,1],步長為0.01;move數據集的區間選取為[0.1,8],步長為0.1.然后對數據集在每個鄰域半徑下進行特征選擇實驗，并采用支持向量機(SVM)和決策樹(DT)這2種分類器對特征子集結果采用十折交叉驗證法計算其分類精度.FSNIFE算法在所有數據集的結果如圖1～8所示.最終的實驗結果選取為分類精度最高且鄰域半徑δ最小的特征子集，由于同一個特征子集在不同分類器下的分類精度并不一樣，因此本實驗會得到2個特征選擇結果，分別為SVM和DT這2種分類器選擇出的特征子集.

Fig. 1 yeast data set result圖1 yeast數據集結果

Fig. 2 wine data set result圖2 wine數據集結果

Fig. 3 mess data set result圖3 mess數據集結果

Fig. 4 wdbc data set result圖4 wdbc數據集結果

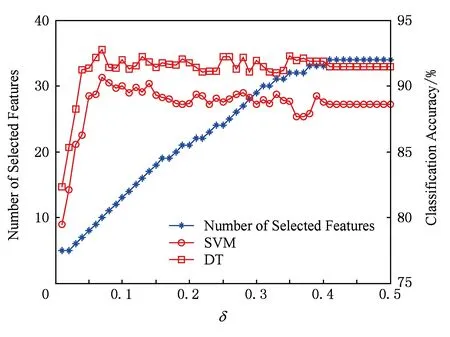
Fig.5 iono data set result圖5 iono數據集結果

Fig. 6 biodeg data set result圖6 biodeg數據集結果

Fig. 7 sonar data set result圖7 sonar數據集結果

Fig. 8 move data set result圖8 move數據集結果

5.2 特征選擇

表3是4種算法在SVM分類器下選擇的特征子集的基數結果，表4是4種算法在DT分類器下選擇的特征子集的基數結果.相比較于原數據集屬性的數目，這4種算法都能很有效地刪去多余的屬性，尤其對于數據集sonar,move.這說明現實中的很多數據集都存在著大量的冗余屬性，從而體現出特征選擇的重要性.另外比較這4種算法的2類特征選擇結果，可以發現在大部分數據集中，本文所提出的FSNIFE算法選擇的特征數目比其他算法要更加的少，說明用FSNIFE算法能更高效地篩選出數據集中少又有效的特征.因此在屬性的約簡基數方面，FSNIFE算法更具優越性.

Table 3 Feature Selection Results of 4 Algorithms in SVM表3 分類器SVM的4種算法特征選擇結果

Table 4 Feature Selection Results of 4 Algorithms in DT表4 分類器DT的4種算法特征選擇結果

5.3 運行時間

Fig. 9 Running time comparison of 4 algorithms in each data set圖9 4種算法在各數據集運行時間比較

圖9展示的是4種算法在所有數據集上特征選擇運行所消耗的時間對比，這個時間是每個算法運行10次后取得的平均時間.由于不同數據集算法消耗時間的數量級不一樣，因此我們分開表示.通過圖9可以看出，相較于其他3種算法，本文所提出的FSNIFE算法所消耗的時間最短.這是由于這4種算法中，FSFRSIE算法和FSFRS算法的時間復雜度為O(c2×n2)，FSFNRS算法的時間復雜度為O(c×n2)，而本文的FSNIFE算法的時間復雜度為O(c3×n×lbn)，其中c表示數據集屬性的數量，n表示對象的數量，因此當c?n時，FSNIFE算法的時間復雜度即為O(n×lbn)，是這4種算法中最低的.因而在實際運用中，FSNIFE算法將會更快速地選擇出特征子集.

5.4 分類精度

為了進一步測試4種特征選擇的性能，我們分別運用支持向量機(SVM)和決策樹(DT)這2種分類器對5.2節中對應的特征選擇結果進行分類訓練，并得到相應的分類精度，重復實驗10次，最終的分類精度采用這10次實驗的均值，所有結果如表5和表6所示.在SVM分類器的分類精度結果中，除了yeast，wine數據集外，其余數據集特征子集的分類精度高于全部特征的分類精度；在DT分類器的分類精度結果中，所有數據集特征子集的分類精度均高于全部特征的分類精度.這說明在數據集中存在很多噪聲數據，這些數據對我們的分類有負面影響，因此，對數據進行特征選擇很有必要.表5和表6中，黑體數值是該行分類精度的最大值.可以看出，表3和表4中FSNIFE算法選擇出的特征子集在大部分數據集具有更高的分類精度.

Table5AverageClassificationAccuracyinSVMofAllFeatureSelectionResultsinTable3

表5表3中所有特征選擇結果在SVM的平均分類精度%

Notes:Bold data represent maximum value.

Table6AverageClassificationAccuracyinDTofAllFeatureSelectionResultsinTable4

表6表4中所有特征選擇結果在DT的平均分類精度%

Notes:Bold data represent maximum value.

綜合特征選擇結果、算法運行時間和分類精度這3個方面，相比于其他3種特征選擇算法，本文提出的FSNIFE算法可以選擇出更少的有效特征，并使對應的分類精度幾乎相等甚至更高，而且算法的運行時間也更短.因此FSNIFE算法對于數據的特征選擇是適合的，相比較于其他算法更具優越性.

由于本文所提的算法時間復雜度為O(c3×n×lbn)，而實驗中選取的均為屬性較少的數據集，因而當數據集屬性的數目遠大于對象的數目時，該算法的計算效率將會變得很低，因此本文所提的特征選擇算法適用于維度較低的數據集，而對于高維的數據并不是很適用.

6 結束語

本文針對目前鄰域粗糙集模型沒有考慮到數據分布問題，首先通過方差刻畫數據的分布情況，并重新定義了二元鄰域空間，使得新的鄰域空間能夠自適應數據的分布；然后提出了自適應二元鄰域空間的粗糙集模型；最后將新提出的模型結合鄰域直覺模糊熵，定義了一種新的特征評估方式，并給出相應的特征選擇算法.UCI實驗結果表明，與現有的算法相比，新提出的算法在特征選擇的數量、算法運行時間和分類精度都有著更高的性能.本文將鄰域半徑取各個值分別計算，然后根據計算結果來尋找最佳的鄰域半徑.接下來需要進一步探索更好的鄰域半徑選取方法.

[1]Han Xiaohong, Chang Xiaoming, Quan Long, et al. Feature subset selection by gravitational search algorithm optimization[J]. Information Sciences, 2014, 281(10): 128-146

[2]Lu Shuxia, Wang Xizhao, Zhang Guiqiang, et al. Effective algorithms of the Moore-Penrose inverse matrices for extreme learning machine[J]. Intelligent Data Analysis, 2015, 19(4): 743-760

[3]Antonelli M, Ducange P, Marcelloni F, et al. On the influence of feature selection in fuzzy rule-based regression model generation[J]. Information Sciences, 2016, 329(1): 649-669

[4]Liang Jiye, Wang Feng, Dang Chuangyin, et al. A group incremental approach to feature selection applying rough set technique[J]. IEEE Trans on Knowledge & Data Engineering, 2014, 26(2): 294-308

[5]Zhang Xiao, Mei Changlin, Chen Degang, et al. Feature selection in mixed data: A method using a novel fuzzy rough set-based information entropy[J]. Pattern Recognition, 2016, 56(1): 1-15

[6]Hu Qinghua, Yu Daren, Liu Jinfu, et al. Neighborhood rough set based heterogeneous feature subset selection[J]. Information Sciences, 2008, 178(18): 3577-3594

[7]Koprinska I, Rana M, Agelidis V G. Correlation and instance based feature selection for electricity load forecasting[J]. Knowledge -Based Systems, 2015, 82: 29-40

[8]Pawlak Z. Rough sets[J]. International Journal of Computer & Information Sciences, 1982, 11(5): 341-356

[9]Duan Jie,Hu Qinghua,Zhang Lingjun,et al.Feature selection for multi-label classification based on neighborhood rough sets[J].Journal of Computer Research and Development, 2015, 52(1): 56-65 (in Chinese)(段潔, 胡清華, 張靈均, 等. 基于鄰域粗糙集的多標記分類特征選擇算法[J]. 計算機研究與發展, 2015, 52(1): 56-65)

[10]Lin T Y. Rough sets, neighborhood systems and approxima-tion[J]. World Journal of Surgery, 1986, 10(2): 189-194

[11]Lin T Y. Granular computing on binary relations I: Data mining and neighborhood systems[J]. Rough Sets in Knowledge Discovery, 1998(2): 165-166

[12]Wang Changzhong, Shao Mingwen, He Qiang, et al. Feature subset selection based on fuzzy neighborhood rough sets[J]. Knowledge-Based Systems, 2016, 111: 173-179

[13]Min Fan,Zhu W. Attribute reduction of data with error ranges and test costs[J]. Information Sciences, 2012, 211(30): 48-67

[14]Zhao Hong, Wang Ping, Hu Qinghua. Cost-sensitive feature selection based on adaptive neighborhood granularity with multi-level confidence[J]. Information Sciences, 2016, 366(20): 134-149

[15]Lin T Y. Granular computing: Practices, theories, and future directions[C]Proc of Encyclopedia on Complexity of Systems Science. Berlin: Springer, 2012: 4339-4355

[16]Zheng Tingting, Zhu Linyun. Uncertainty measures of neighborhood system-based rough sets[J]. Knowledge-Based Systems, 2015, 86(C): 57-65

[17]Atanassov K T. Intuitionistic fuzzy sets[J]. Fuzzy Sets & Systems, 1986, 20(1): 87-96

[18]Szmidt E, Kacprzyk J. Entropy for intuitionistic fuzzy sets[J]. Fuzzy Sets & Systems, 2001, 118(3): 467-477

[19]Vlachos I K, Sergiadis G D. Intuitionistic fuzzy information-applications to pattern recognition[J]. Pattern Recognition Letters, 2007, 28(2): 197-206

[20]Zhang Huimin . Entropy for intuitionistic fuzzy sets based on distance and intuitionistic index[J]. International Journal of Uncertainty Fuzziness and Knowledge-Based Systems, 2013, 21(1): 181-196

[21]Chen Yumin, Wu Keshou, Chen Xuhui, et al. An entropy-based uncertainty measurement approach in neighborhood systems[J]. Information Sciences, 2014, 279(20): 239-250

[22]Zhang Zhenhai,Li Shining,Li Zhigang,et al.Multi-label feature selection algorithm based on information entropy[J].Journal of Computer Research and Development, 2013, 50(6): 1177-1184 (in Chinese)(張振海, 李士寧, 李志剛, 等. 一類基于信息熵的多標簽特征選擇算法[J]. 計算機研究與發展, 2013, 50(6): 1177-1184)

[23]Wei Wei, Liang Jiye, Qian Yuhua, et al. Can fuzzy entropies be effective measures for evaluating the roughness of a rough set?[J]. Information Sciences, 2013, 232(5): 143-166

[24]Zhao Hua, Qin Keyun. Mixed feature selection in incomplete decision table[J]. Knowledge-Based Systems, 2014, 57(2): 181-190

[25]Wang Changzhong, Qi Yali, Shao Mingwen, et al. A fitting model for feature selection with fuzzy rough sets[J]. IEEE Trans on Fuzzy Systems, 2017, 25(4): 741-753

[26]Liu Yong, Huang Wenliang, Jiang Yunliang, et al. Quick attribute reduct algorithm for neighborhood rough set model[J]. Information Sciences, 2014, 271(1): 65-81

YaoSheng, born in 1979. PhD. Lecturer, master supervisor. Her main research interests include rough set, granular computing, big data.

XuFeng, born in 1993. Master candidate. His main research interests include rough set, granular computing, big data.

ZhaoPeng, born in 1976. PhD. Associate professor, master supervisor. Her main research interests include intelligent information processing (zhaopeng_ad@ahu.edu.cn).

JiXia, born in 1983. PhD. Lecturer, master supervisor. Her main research interests include rough set (jixia1983@163.com).