分類討論思想在高中數學解題中的應用

王奎鈞

（山東省莒南第一中學 276600）

引言

高中階段的數學知識比較抽象復雜，如果我們在學習解題中，運用一成不變的思維邏輯，不僅增加了學習難度，還會出現各種問題。因此就要學會靈活運用分類討論思想，實現快速解決數學習題。

一、分類討論思想在高中數學解題中的價值

分類討論思想，就是指在我們解題的過程中，可以將問題劃分為多種情況，我們只需要抓住問題的主要因素，進而來確定變化條件的范圍以及問題的發展方向，就能夠根據各種情況來進行分類討論，運用分類討論思想。在分類思想運用過程中，首先要樹立分類意識，要確定如何分類和分類研究，在對分類的結果進行整合分析。運用分類思想解高中數學習題，能夠不斷提高我們的邏輯思維能力。由于高中階段的數學知識內容都相對比較抽象，因此在解題過程中難度就會增加，只要運用分類討論思想，將數學問題的發展方向進行把握，就可以提高解題效率，提高解題正確率。[1]

二、分類討論思想的標準劃分

在高中數學解題中，隨著分類討論思想的應用不斷增多，就能夠為我們更加快速而準確的解答數學習題創造良好的條件。因此首先需要對分類思想的標準進行準確詳細劃分，這樣才能提高我們的數學成績。[2]

首先需要按照數學的概念知識進行科學合理的劃分，在學習過程中，很多知識內容都是按照分類思想定義的。其次要按照運算法則、定理、公式等進行劃分。最后按照圖形位置進行合理劃分。在圖形習題的解題中，應用分類討論思想比較多，比如函數和幾何圖形等。

三、分類討論思想在高中數學解題中的具體應用

1.在函數解題中的應用

函數習題一直都是數學高考的熱門考點，無論是選擇題、填空題還是解答題，都有與函數相關的題目，這也為我們學習函數增加了壓力。在函數學習中，我們不僅要區分掌握基本的函數形式，還要培養自身的解決疑難函數題目的能力。將分類討論思想應用到函數解題中，就能夠幫助我們用專業的、學科的思維方式進行學習，能夠提高學習效率和學習成績。將分類討論思想思想運用到函數解題中，有利于我們將函數實際問題，從而更好的將所學知識運用在生產生活實踐中。

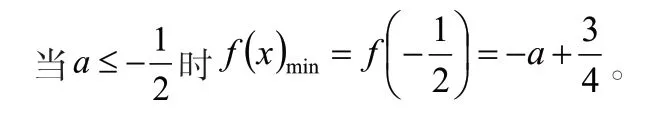
2.在概率解題中的應用

概率在我們的日常生活中隨處可見，概率是研究隨機現象規律的學科，它為人們認識客觀世界提供了重要的思維模式和解決問題的方法，并且為統計學的發展提供了基礎理論。我們在高中階段所學習的概率主要是了解隨機現象與概率的意義，在概率基本性質和簡單概率模型的基礎上，加深對隨機現象的理解，并且學習用隨機模擬的方法估計簡單隨機事件發生的概率。因此將分類討論思想應用在概率學習中，能夠加深我們對于隨機現象的理解，了解隨機事件發生的不確定和頻率的穩定性，從而幫助我們正確理解概率的意義。[3]

將分類討論思想應用在概率解題中，我們首先要從問題的本身入手，確定問題的概率類型，其次對已知條件中的各個數進行編號排列，最后在對各個可能性數值進行假設，得出結論。

解析：當x＜－1時，不等式化為－x－1＋x－2≥1，此時無解；

當－1≤x≤2時，不等式化為x＋1＋x－2≥1，解得x≥1；

當x＞2時，不等式化為x＋1－x＋2≥1，此時恒成立；

∴|x＋1|－|x－2|≥1的解集為[1，＋∞）；

在[-3，3]上使不等式有解的區間為[1，3]，

3.在數列解題中的應用

高中數列方面的知識內容，是高中數學學習的基礎內容，處于一個知識匯合點的地位，與很多知識都有著密切的聯系，還能給幫助我們復習深化方程問題、一次函數、二次函數問題、等比性質等，很多重要的數學問題都能夠通過數列得到圓滿解決。數列在高中數學學習中，也占據著非常重要的地位，數列問題的學習能夠培養我們對數學問題的思考、分類和歸納能力，對以后的數學學習有著啟蒙作用。例如在認識數列時，將分類討論思想引入到學習中，可以對數列進行動態認識。在等差數列的單調性學習、求和最值學習中，都可以將分類討論思想引用到其中，可以提高我們的解題效率，提高解題正確率。

結語

綜上所述，在高中數學的學習過程中，有很多重難點知識，不僅需要記憶掌握，還要靈活運用。分類討論思想可以運用在數列解題中，運用在函數解題中，運用在概率解題中等等。因此在今后的學習中，我們就要靈活運用分類討論思想，來提高我們的學習成績。