某異形景觀橋人致振動荷載取值及舒適度分析

張雪松，陳永輝，王繼祥

(重慶交通大學(xué) 土木工程學(xué)院，重慶 400074)

橋梁結(jié)構(gòu)振動，是伴隨著外作用輸入(車輛動荷載、人群動荷載、風(fēng)力、地震波)，結(jié)構(gòu)體系變形能量和運(yùn)動能量相互轉(zhuǎn)換的周期性過程。汽車荷載通過沖擊力系數(shù)達(dá)到了對車輛靜荷載的放大作用，而沖擊系數(shù)由結(jié)構(gòu)固有頻率決定。隨著新型材料與施工工藝的使用，橋梁結(jié)構(gòu)不斷向著大跨、懸挑等更輕柔、阻尼更小的方向發(fā)展。對于以人群荷載為主的人行橋，其動力特性較復(fù)雜，在人行荷載作用下，會發(fā)生一定程度的振動，使人產(chǎn)生不舒適感。通過建立動力學(xué)數(shù)學(xué)模型，采用時域法或頻域法分析人體不同部位對外界振動的響應(yīng)[1]。故如何使橋體在保證強(qiáng)度、剛度和穩(wěn)定性的同時滿足舒適度要求已成為結(jié)構(gòu)設(shè)計的重點(diǎn)、難點(diǎn)。

結(jié)構(gòu)振動舒適度評價標(biāo)準(zhǔn)主要分為兩類：計算橋體振動特性，為防止人與人行橋共振，減少行人不舒適感，避免發(fā)生危險事故，要求天橋上部結(jié)構(gòu)豎向自振頻率不應(yīng)小于3 Hz[2]；分析外部荷載激勵下的振動響應(yīng)，采用傅立葉級數(shù)來表示人行荷載激勵[3]。

1　工程概況

1.1　工程概況及結(jié)構(gòu)參數(shù)

擬建工程為懸挑式景觀玻璃橋(圖1)，平臺布置于場地陡崖邊緣向外懸挑長度達(dá)70 m，采用46根拉索將橋塔與玻璃平臺連接成為空間異形結(jié)構(gòu)，作為旅游觀光設(shè)施極具視覺沖擊力。該工程為國內(nèi)最大跨度懸挑景觀橋，其結(jié)構(gòu)自振頻率較低，特殊的結(jié)構(gòu)形式?jīng)Q定了在人行荷載激勵下極易發(fā)生共振和行走舒適度較差等問題。玻璃橋主要結(jié)構(gòu)為鋼管、鋼箱梁、鋁合金挑梁、玻璃，主要結(jié)構(gòu)參數(shù)見表1。

圖1　成橋效果Fig. 1　Bridge effect diagram

表1　主要結(jié)構(gòu)參數(shù)Table 1　Main configuration parameters

1.2　橋體振動特性

新型材料及異形結(jié)構(gòu)形式易引起人群舒適度較差等問題。故需要對景觀橋進(jìn)行人致振動分析，并評估其舒適度級別，并依此提出相應(yīng)的減震措施。初步設(shè)計階段通過改變截面或結(jié)構(gòu)形式以提高全橋整體、局部剛度，從而減少活載變形、增大自振基頻。從活載撓度、動力特性兩個方面對比以下結(jié)構(gòu)形式：

1) 原結(jié)構(gòu)(主橋部分鋼管采用φ0.4×0.025)；

2) 主橋所有鋼管均采用φ0.4×0.025；

3) 在原結(jié)構(gòu)形式上，拉索直徑修改為7.5 cm；

4) 所有鋼管采用φ0.4×0.025，拉索直徑為7.5 cm；

5) 優(yōu)化后結(jié)構(gòu)(在原結(jié)構(gòu)主橋頂面、底面做平聯(lián))如圖2，其交叉線條即為平聯(lián)結(jié)構(gòu)。

圖2　優(yōu)化后主橋效果Fig. 2　Main bridge effect diagram after optimization

表2　不同方案結(jié)構(gòu)響應(yīng)匯總Table 2　Summary of structure response of different programs

筆者通過對主橋結(jié)構(gòu)形式優(yōu)化：頂、底面增加平聯(lián)桿件使其成為“封閉箱梁”形式，增大全橋抗扭剛度，玻璃橋自振頻率增幅明顯，活載變形大大減小。但全橋豎向自振頻率仍小于3 Hz，無法滿足要求；若仍采用豎向結(jié)構(gòu)基頻控制大跨人行橋設(shè)計則顯得較為嚴(yán)格。同時研究表明：在一定情況下，即使結(jié)構(gòu)基頻落入人群振動敏感區(qū)時，也可滿足人群舒適度要求[4]。在結(jié)構(gòu)響應(yīng)中：振動位移、速度和加速度這3要素，加速度對人生理和心理感受影響最大，直接決定了人行走舒適度，因而建議采用振動響應(yīng)加速度進(jìn)行舒適度評價。加速度參數(shù)在實(shí)際工程中有廣泛應(yīng)用，如橋梁基礎(chǔ)沖孔樁施工中引進(jìn)地表振動加速度，以分析沖擊能對振動速度的影響[5]。

人行荷載作為一種動力荷載，是人行橋振動最主要的激勵來源，步行荷載動力特性是影響結(jié)構(gòu)振動分析精度與振動控制效果最主要的因素。由于行人具有自主性，其在橋面上分布具有隨機(jī)性，故人行荷載模擬是當(dāng)前世界范圍內(nèi)人行橋研究的難點(diǎn)。國外學(xué)者已對人群荷載取值做了相應(yīng)要求，由于國內(nèi)人群身高、體重等特征參數(shù)與西方國家人群有較大差異，直接采用國外人群荷載取值必將引起較大誤差。因此，以國人體質(zhì)為基礎(chǔ)，建立和研究人群荷載模型，具有必要性和迫切性。

2　步行力產(chǎn)生原理及特點(diǎn)

2.1　步行力產(chǎn)生原理

步行，按照生物力學(xué)觀點(diǎn)就是人體在行進(jìn)過程中，全身肌肉都同時參與工作。步行者在行走過程中，身體重心沿復(fù)雜的螺旋形曲線向前運(yùn)動。行走時左、右兩足跟之間的向距離稱為步長，橫向距離稱為橫距。于國內(nèi)人群而言，成年男性每復(fù)步一般為150～160 cm[6]。

行進(jìn)過程中，人體重心上下、左右擺動，產(chǎn)生豎向周期性荷載激勵，荷載頻率等同于步行荷載頻率。在雙腿交替行進(jìn)過程中，人體重心會發(fā)生“Z”字形左右擺動，產(chǎn)生水平側(cè)向動力荷載，其頻率為步頻的一半。任一時刻行人對景觀橋的動力荷載不同，從而產(chǎn)生一個動態(tài)的時程力，包括豎向時程力、縱向時程力、橫向時程力。由于豎向時程力對結(jié)構(gòu)影響最大，筆者以該方向時程力進(jìn)行分析，其余方向時程力類比于豎向時程力。

筆者將人群荷載分解為3個方向分量形式，各方向時程曲線如圖3。其中：圖3(a)為豎向力時程；圖3(b)為橫向力時程；圖3(c)為縱向力時程[7]。由圖3(a)可看出：豎向力時程具有兩個波峰和一個波谷；在人類行進(jìn)過程中，需雙腿交替運(yùn)動，兩下肢交替運(yùn)動，帶動整個身體前進(jìn)。

圖3　單步力3方向分量的時程Fig. 3　Time history of the three direction component of a single step force

2.2　步行力特點(diǎn)

人行荷載不同于其他可變荷載，具有以下特點(diǎn)[8-9]。

2.2.1顯著的周期性

人行荷載具有明顯的周期性，成年人正常行走時的步頻在1.6～2.4 Hz，豎向力前3階諧波都可能激發(fā)橋梁振動；橫向力步行力頻率在3.2～4.8 Hz，橫向力則一般只考慮1階諧波作用。

2.2.2窄帶隨機(jī)過程

由于行人荷載的特殊性，其步長、頻率變化程度沒有其他可變荷載(如汽車荷載、地震荷載等)劇烈，步行步長、頻率均是在很窄范圍內(nèi)隨機(jī)分布。當(dāng)橋上行人較多時，隨著基數(shù)增大，必將導(dǎo)致初相位相等的人越來越多，若此時這群人的腳步頻率與橋梁結(jié)構(gòu)自振頻率接近甚至相同時，橋梁就會產(chǎn)生明顯振動，進(jìn)而影響行人舒適度甚至結(jié)構(gòu)破壞。

2.2.3人橋“互動”

行人即是結(jié)構(gòu)的激振源，又是感受體。若人行橋發(fā)生振動，將嚴(yán)重地影響到行人的步行舒適性及安全性，部分行人會停下來依靠橋上欄桿來保持平衡，更多人群會通過調(diào)整自己步頻、步長等方式來適應(yīng)橋梁振動和改善自己行走舒適度，這種現(xiàn)象稱為“集體同步”現(xiàn)象[10-11]，這種行為反而會加劇橋梁橫向振動。

3　人行荷載模型

作為人行橋振動的主要激勵來源，人行荷載對人行橋振動機(jī)理研究起著至關(guān)重要作用，必須建立合理的行人腳步荷載數(shù)學(xué)模型，F(xiàn).C.HARPER等[12-13]采用測力板對人行荷載測量做了研究。目前學(xué)界建立的單人腳步荷載時域數(shù)學(xué)模型有兩類：確定性模型和隨機(jī)性模型。確定性荷載模型相對簡單，國外在人行橋動力設(shè)計中普遍采用確定性模型對結(jié)構(gòu)進(jìn)行評估。

3.1　單人荷載模型

人行荷載具有顯著周期性，其豎向力和側(cè)向力都可用無窮級數(shù)(傅里葉級數(shù))的形式表達(dá)出來[14]。

豎向步行力模型如式(1)：

(1)

側(cè)向步行力模型如式(2)：

(2)

式中：t為時間；W為體重；fp為步行荷載頻率；αvi為第i階豎向力動載因子；αli為第i階側(cè)向力動載因子；φvi為第i階豎向力諧波相位角；φli為第i階側(cè)向力諧波相位角。

表3羅列了各國學(xué)者提出或經(jīng)試驗測得的各階諧波動載因子。

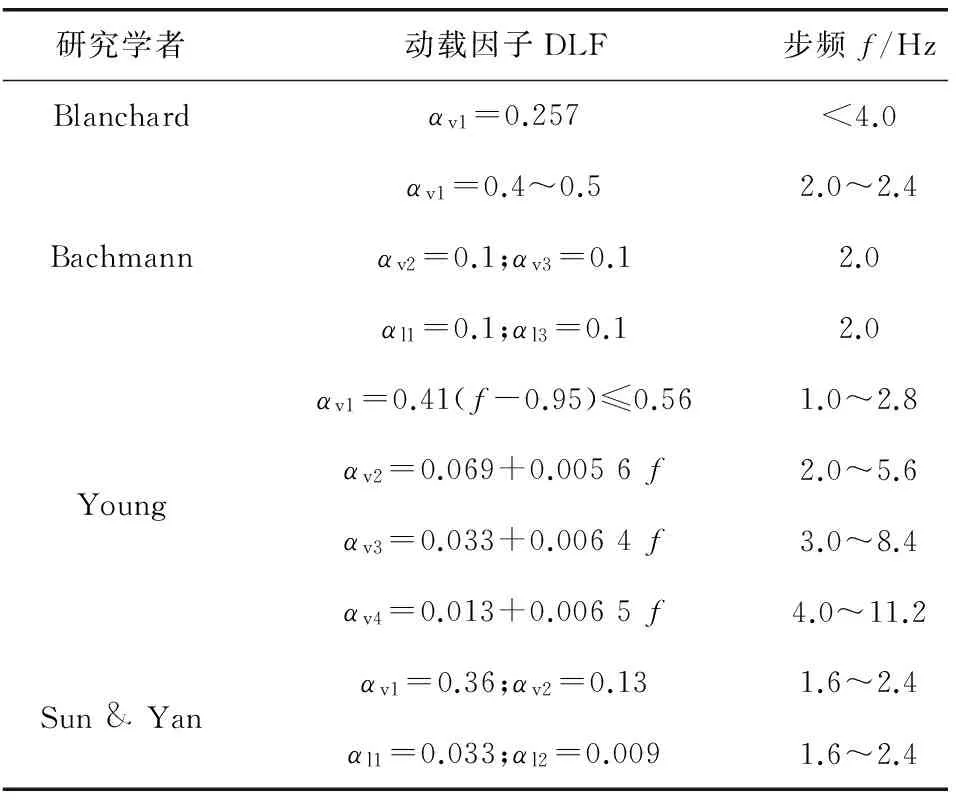
表3　不同學(xué)者提出的單人動載因子(DLF)Table 3　Dynamic load factor(DLF) proposed by different scholars

由表3可知：豎向1階諧波動載因子最大，對結(jié)構(gòu)振動貢獻(xiàn)最大，高階諧波動載因子迅速減小，在滿足工程要求前提下只需考慮前3階或前4階動載因子引起的激勵荷載。

3.2　多人荷載模型

多人荷載模型相對于單人荷載模型更為復(fù)雜，隨著橋上人數(shù)增多，其行走過程的隨機(jī)性也逐漸增大。由于人群初相位不同，動力荷載并不能簡單等同于單人動力荷載乘橋上人群總數(shù)，而要小于該值。因此不能直接使用單人荷載動載因子，依據(jù)表4不同人群密度，人群荷載動載因子α*也有區(qū)別。

表4　多人荷載類型劃分Table 4　Partition of multi-person load type

3.2.1小組結(jié)伴而行

豎向腳步動荷載的一階諧波分量很容易實(shí)現(xiàn)同步，假定小組人群行走完全同步，但2階、3階諧波引起同步的可能性很小，簡化計算時其效應(yīng)可忽略。人群荷載模型的動載因子與單人荷載的動載因子相同，即α*=α，小組行人步行力模型可用式(3)所采用的單人荷載模型乘以小組人數(shù)來計算。

Fp=W·α·sin(2πfp·t)·n

(3)

3.2.2低密度人群自由行走

(4)

3.2.3高密度人群流動

(5)

4　景觀玻璃橋人致振動舒適度分析

玻璃橋采用自振頻率控制設(shè)計是不現(xiàn)實(shí)的。故筆者采用動力響應(yīng)評價方法，利用結(jié)構(gòu)在人行荷載激勵下的峰值加速度來對其進(jìn)行舒適度評價。

動力設(shè)計基本過程為[15]：依據(jù)結(jié)構(gòu)動力特性，確定敏感頻率范圍；人致振動響應(yīng)分析，以外界激勵荷載引起結(jié)構(gòu)最大加速度評估舒適性級別，舒適性級別見表5。

表5　人行橋的加速度舒適性判定標(biāo)準(zhǔn)Table 5　Judging criteria of the acceleration comfort of a footbridge

4.1　人群荷載模擬

時程分析法可準(zhǔn)確確定在外界荷載激勵下結(jié)構(gòu)內(nèi)力、位移加速度等響應(yīng)隨時間的反應(yīng)，其缺點(diǎn)主要是對計算機(jī)配置要求高，計算周期長。時程分析加載形式有固定點(diǎn)加載法、移動加載法，初步設(shè)計階段采用固定荷載法計算人群激勵下的最大響應(yīng)。依據(jù)人群活載影響面(線)數(shù)據(jù)、振型模態(tài)，采用等效原則將壓力荷載轉(zhuǎn)換為節(jié)點(diǎn)荷載固定施加在引起最大加速度的點(diǎn)上。

本橋相鄰兩階振型的自振頻率比較接近，且前4階模態(tài)均位于活載敏感頻率范圍，故激勵荷載分別采用1.50、1.75、2.00、2.25、2.50、2.75、3.00、3.25、3.50 Hz，以期進(jìn)行掃頻分析，行人質(zhì)量取為75 kg，人群密度取1人/m2。選取具有代表性的3個節(jié)點(diǎn)：節(jié)點(diǎn)1330(主橋右側(cè))、節(jié)點(diǎn)1331(主橋左側(cè))和節(jié)點(diǎn)1941(主橋最前端)進(jìn)行分析，分別對比不同頻率激勵荷載作用下各點(diǎn)的豎向加速度值，如圖4。

圖4　時程力加載及觀測點(diǎn)Fig. 4　Diagram of time history force loading and observation points

根據(jù)對人行荷載描述，該景觀玻璃橋考慮不利工況為：高密度人群流動。

玻璃橋面寬取用3.8 m，相鄰挑梁間距2.4 m，故面積為3.8×2.4=9.12 m2，相鄰挑梁之間橋上近似為9人。根據(jù)表6不同頻率各階動載因子，得出式(6)的等效節(jié)點(diǎn)力。

(6)

表6　不同荷載頻率的動載因子Table 6　Dynamic load factor of different load frequency

4.2　動力時程分析

人群激勵荷載頻率為1.5 Hz，人行荷載激勵下選取1330、1331、1941這3個節(jié)點(diǎn)的豎向加速度時程，如圖5。

圖5　節(jié)點(diǎn)加速度時程Fig. 5　Time history of node acceleration

限于篇幅，筆者不再一一列出其余荷載激勵，對各點(diǎn)在不同頻率下，加速度峰值進(jìn)行掃頻分析，具體結(jié)果見圖6。

圖6　觀測點(diǎn)加速度峰值掃頻分析結(jié)果Fig. 6　Sweep-frequency analysis results of acceleration peak values of observation points

5　結(jié)論及展望

使用傅立葉三角級數(shù)將腳步力等效為外界激勵加載到結(jié)構(gòu)上進(jìn)行時程計算，對觀測點(diǎn)進(jìn)行加速度掃描分析，有如下結(jié)論：

1) 當(dāng)增加截面尺寸不能顯著改善結(jié)構(gòu)動力響應(yīng)時，通過優(yōu)化部分結(jié)構(gòu)形式可使得活載撓度、自振基頻達(dá)到預(yù)想結(jié)果；

2) 控制結(jié)構(gòu)豎向基頻不應(yīng)小于3 Hz過于嚴(yán)格，必將引起資源浪費(fèi)。參閱相關(guān)文獻(xiàn)，采用各階動載因子參數(shù)，將腳步力荷載等效為各階正弦函數(shù)代數(shù)和的形式。對結(jié)構(gòu)進(jìn)行動力響應(yīng)分析，以加速度控制人群舒適度級別；

3) 基于振型模態(tài)、活載影響面(線)確定固定荷載加載點(diǎn)，初步設(shè)計階段，采用定點(diǎn)加載法比移動荷載法效率更高，且當(dāng)結(jié)構(gòu)頻率較低時，固定荷載法的結(jié)果相對更保守；

4) 由加速度峰值掃描分析結(jié)果，驗證了外界激勵等于或接近結(jié)構(gòu)豎向基頻時，振動幅度最大，極易發(fā)生共振；

5) 加速度峰值較大時，易引起人群不舒適感，嚴(yán)重時會導(dǎo)致橋梁毀壞，建議加裝TMD阻尼器。

參考文獻(xiàn)(References)：

[1]錢凱，胡啟國，李力克.基于人-車-路耦合振動系統(tǒng)的兒童乘坐舒適性[J].重慶交通大學(xué)學(xué)報(自然科學(xué)版)，2013，32(2)：351-359.

QIAN Kai，HU Qiguo，LI Like.Children ride comfort based on human-vehicle-road coupled system of vibration[J].JournalofChongqingJiaotongUniversity(NaturalScience)，2013，32(2)：351-359.

[2]北京市市政工程研究院.城市人行天橋與人行地道技術(shù)規(guī)范：CJJ 89—95[S].北京：中國建筑工業(yè)出版社，1996.

Beijing Municipal Engineering Research Institute.TechnicalSpecificationofUrbanPedestrianOvercrossingandUnderpass：CJJ89—95[S].Beijing：China Architecture & Building Press，1996.

[3]BACHMANN H，PRETLOVE A J，RAINER H.DynamicForcesfromRhythmicalHumanBodyMotions[M].Basel：Birkhause Verlag，1995.

[4]孫滬.異形鋼拱人行橋通行舒適度及其控制研究[D].杭州：浙江工業(yè)大學(xué)，2015.

SUN Hu.TheResearchonTrafficComfortIndexandVibrationComfortControlofSpecial-shapedSteelArchFootbridge[D].Hangzhou：Zhejiang University of Technology，2015.

[5]佘艷華，蘇華友，肖正學(xué)，等.橋梁樁基沖孔樁施工的微振動響應(yīng)研究[J].重慶交通大學(xué)學(xué)報(自然科學(xué)版)，2011，30(1)：35-38.

SHE Yanhua，SU Huayou，XIAO Zhengxue，et al.Study on the vibration response to punched pile construction of bridge pile foundation[J].JournalofChongqingJiaotongUniversity(NaturalScience)，2011，30(1)：35-38.

[6]錢競光，宋雅偉，葉強(qiáng)，等.步行動作的生物力學(xué)原理及其步態(tài)分析[J].南京體育學(xué)院學(xué)報(自然科學(xué)版)，2006，5(4)：1-7.

QIAN Jingguang，SONG Yawei，YE Qiang，et al.The biomechanics principle of walking and analysis on gaits[J].JournalofNanjingInstituteofPhysicalEducation(NaturalScience)，2006，5(4)：1-7.

[7]袁旭斌.人行橋人致振動特性研究[D].上海：同濟(jì)大學(xué)，2006.

YUAN Xubin.ResearchonPedestrian-InducedVibrationofFootbridge[D].Shanghai：Tongji University，2006.

[8]劉軍進(jìn)，肖從真，潘寵平，等.跳躍和行走激勵下的樓蓋豎向振動反應(yīng)分析[J].建筑結(jié)構(gòu)，2008，38(11)：108-110.

LIU Junjin，XIAO Congzhen，PAN Chongping，et al.Investigation on response of floor vibration under jumping and walking excitation[J].BuildingStructure，2008，38(11)：108-110.

[9]陳政清.人行橋的振動與動力設(shè)計[M].北京：人民交通出版社，2009.

CHEN Zhengqing.VibrationandDynamicDesignofPedestrianBridge[M].Beijing：China Communications Press，2009.

[10]DALLARD P，F(xiàn)ITZPATRICK A，F(xiàn)LINT A，et al.The London MillenniumFootbridge[J].StructuralEngineer，2001，79(171)：17-33.

[11]DALLARD P，F(xiàn)ITZPATRICK A，F(xiàn)LINT A，et al.London Millennium Bridge：pedestrian-induced lateral vibration[J].JournalofBridgeEngineering，2001，6(6)：412-417.

[12]HARPER F C.The mechanics of walking[J].ResearchAppliedinIndustry，1962，15(1)：23-28.

[13]HARPER F C，WARLOW W J，CLARKE B L.The force applied to the floor by the foot in walking[J].NationalBuildingStudies，1961，12(1)：32-38.

[14]PAVIC A，REYNOLDS P.Vibration serviceability of long-span concrete building floors，part1：review of background information[J].Shock&VibrationDigest，2002，34(3)：191-211.

[15]HIVOS S.GuideLineforDesignforFootbridge[R].U.S.A.：HIVOSS，2007：1-33.