基于因子分析與突變級數法的飛行安全狀態評價研究*

王永剛，蘇明清

(1.中國民航大學 安全學部，天津300300；2. 中國民航大學 經濟與管理學院，天津 300300)

0　引言

飛行安全是民航安全工作的核心，也是航空公司一切發展的前提條件。科學合理的評價體系有助于航空公司快速準確地掌握飛行安全狀態，找出其中存在的不安全因素，進而采取針對性的措施，預防和減少飛行不安全事件的發生。

國內外學者對飛行安全評價的研究主要有兩類，一類是從人員、航空器、組織、環境、管理等方面對飛行安全的狀態進行綜合評價。James等[1]從管理、運行、維修、事故率4個方面建立評價指標體系，采用網絡層次分析法(ANP)和決策試驗與實驗室法(DEMATEL)，確定了指標間的相互關系及其權重；Ahmadi等[2]從飛機維修的角度出發，結合事件樹分析方法，對成本約束下的航空公司飛行安全進行了評價；唐衛貞[3]從“人—機—環—管”4個方面來建立指標體系，構建了航空公司飛行安全評價的多級物元模型，從而確定出影響航空公司飛行安全的主要因素；陳可嘉等[4]在建立指標體系后，利用三角白化權函數建立了灰色區間層次評價法，實現了對飛行安全的綜合評價。通過“人—機—環—管”等方面對飛行安全狀態進行評價，建立的指標體系可以較為全面地描述影響飛行安全的因素，但指標權重的客觀準確性受人為主觀的干擾。飛行員的操作行為與飛行安全有直接關系，該方法也無法對飛行員的操作行為進行評價分析，不利于后續飛行安全水平的提升。另一類是以飛機的快速存取記錄器(QAR， quick access recorder)上所記錄的數據作為飛行安全狀態的評價依據。Sembiring等[5]采用最小二乘法和最大似然估計，基于QAR數據對反映飛行安全狀態的飛機升力以及阻力系數進行了參數估計；Wang等[6]通過對進近和著陸階段的QAR數據進行分析，建立了接地點遠事件的風險評價模型；高揚等[7]選取飛行過程中發生率較高的幾個超限事件作為指標來建立評價指標體系；周長春[8]等選取了3項QAR超限事件作為評價指標，對飛機進近著陸階段的安全性進行評估。將QAR超限事件作為評價指標能客觀反映出飛行狀況，但現有文獻中只是直接選取某些指標進行評價，導致建立的評價指標體系不完整，也沒有考慮指標間的相關性造成的重復評價，這些都影響了評價的準確性。

基于此，本文首先選取所有QAR超限事件作為原始指標，采用因子分析法對其進行相關性研究，并提取超限事件的公共因子來構建飛行安全狀態評價指標體系。針對飛行不安全事件具有不確定性和突變性的特點[9]，引入無需確定指標權重的突變級數法建立評價模型。最后，收集航空公司實際運行數據對該模型的有效性進行驗證。

1　研究方法的確定

1.1　因子分析法

為了完善飛行安全狀態的評價指標體系，應將擬評價時期內所有發生的QAR超限事件作為評價指標。QAR超限事件監測的參數通常包括速度、加速度、高度、俯仰角、下降率等參數。飛行員在飛行中是通過操縱駕駛桿(盤)和腳蹬來實現對飛機的控制[10]。在不同的飛行階段，QAR所記錄的事件往往具有一定的相關性。因此，如果直接用這些指標進行評價，不僅會由于指標數過多導致模型復雜，而且還會因指標間的多重共線性造成誤差。因子分析法可以從多個相關變量中找出少數幾個公共因子來解釋原始數據，客觀地確定綜合指標。據此，采用因子分析法，對不同飛行階段的QAR超限事件進行相關性研究，并提取超限事件的公共因子來構建飛行安全狀態的評價指標體系。

1.2　突變級數法

建立評價指標體系后，一般需要確定各項指標的權重進行評價。權重的確定容易受到人工打分等主觀因素干擾。此外，在實際的飛行運行中，各項評價指標的權重會受環境等多種因素的限制和影響。所以，飛行運行作為一個動態發展的過程，事先確定精確的權重值并不適合其安全狀態的評價。突變級數法不需要事先確定權重，只需要確定各項指標的重要性排序。在本文中，可以依據因子分析法中所提取的公共因子的貢獻率大小來確定指標重要性排序。突變級數法在水環境評價[11]、工程應用[12]、項目決策[13]等方面已得到廣泛運用，其原理是突變理論，該理論主要研究非連續的、突然的變化，如生物的變異、災害的突發等[14]。

突變理論將系統的狀態參數稱為狀態變量，將影響系統狀態的變量稱為控制變量(行為變量)。所以在建立評價的指標體系時，上一層的評價目標可看作是狀態變量，其對應的下一層評價指標可看作是對應的控制變量。不同數量的狀態變量和控制變量對應突變理論中不同的突變模型，其勢函數和歸一公式也不同。常用的突變模型見表1。具體運算時，同一狀態變量對應的控制變量的合成一般遵循2個原則：互補原則，若控制變量之間可以相互補充，所起的作用能夠疊加，則取這些控制變量的平均值作為其對應狀態變量的隸屬度值；非互補原則，若控制變量之間不可以相互代替，則取這些控制變量中值最小的一個作為其對應狀態變量的隸屬度值[15]。

表1　常用的突變模型Table 1　Common catastrophe models

2　模型構建

2.1　確定飛行安全狀態的評價指標

以某航空公司A320 機型的QAR數據為研究對象，選取2011—2014年度60個月的數據作為原始數據。在一次完整的飛行任務中，可將飛行過程分為起飛滑跑、爬升、巡航、下降進近、進場著陸等幾個階段。每個飛行階段中飛行員的操作負荷、飛機構型以及狀態參數等不盡相同。據此，可將每個飛行階段的安全狀態作為一級指標分別進行評價。巡航階段時飛機操縱穩定，QAR超限事件幾乎不發生，在評價中將其與爬升階段合并。因此，飛行安全狀態評價指標體系的一級指標為：滑跑起飛階段安全狀態、爬升巡航階段安全狀態、下降進近階段安全狀態、進場著陸階段安全狀態。其中，事件發生率的計算公式如下：

(1)

選取各飛行階段的超限事件種類數如表2所示。

表2　各飛行階段超限事件種類數Table 2　The number of exceedance events ateach flight phase

以進場著陸階段為例，運用因子分析法提取公共因子來構建該子系統的評價指標體系。

2.1.1數據相關性檢驗

因子分析前需進行相關性檢驗，一般使用KMO測度和Bartlett球度檢驗這兩個統計量。當KMO測度的值大于0.7時，比較適合做因子分析[16]。將原始數據導入SPSS20.0軟件中，該分析軟件能自動對數據進行標準化，計算出相關性檢驗的數據如表3所示。

表3　KMO檢驗和Bartlett檢驗Table 3　The test of KMO and bartlett

由表3可知，KMO測度的值為0.791，表明適合做因子分析。同時，Bartlett球度檢驗統計量的值為1 385. 883，顯著性水平遠低于0.05，可拒絕Bartlett球形檢驗的零假設，說明相關系數矩陣不是單位陣，也比較適合做因子分析。

2.1.2公因子選取及命名

接著計算得出公因子的特征值和方差貢獻率以及累計貢獻率如表4所示。當按照特征值大于1來選取公因子時，可得到3個公因子，累積貢獻率為77.254%。這表明，此時選取的3個公因子能夠較好地反映樣本所含信息。選取公因子后，采用正交旋轉中的方差最大法對初始因子載荷矩陣進行旋轉，以便對公因子進行解釋和命名，命名后的公因子即可作為進場著陸階段飛行安全狀態的評價指標。表5為旋轉后的因子載荷矩陣和因子得分系數矩陣。

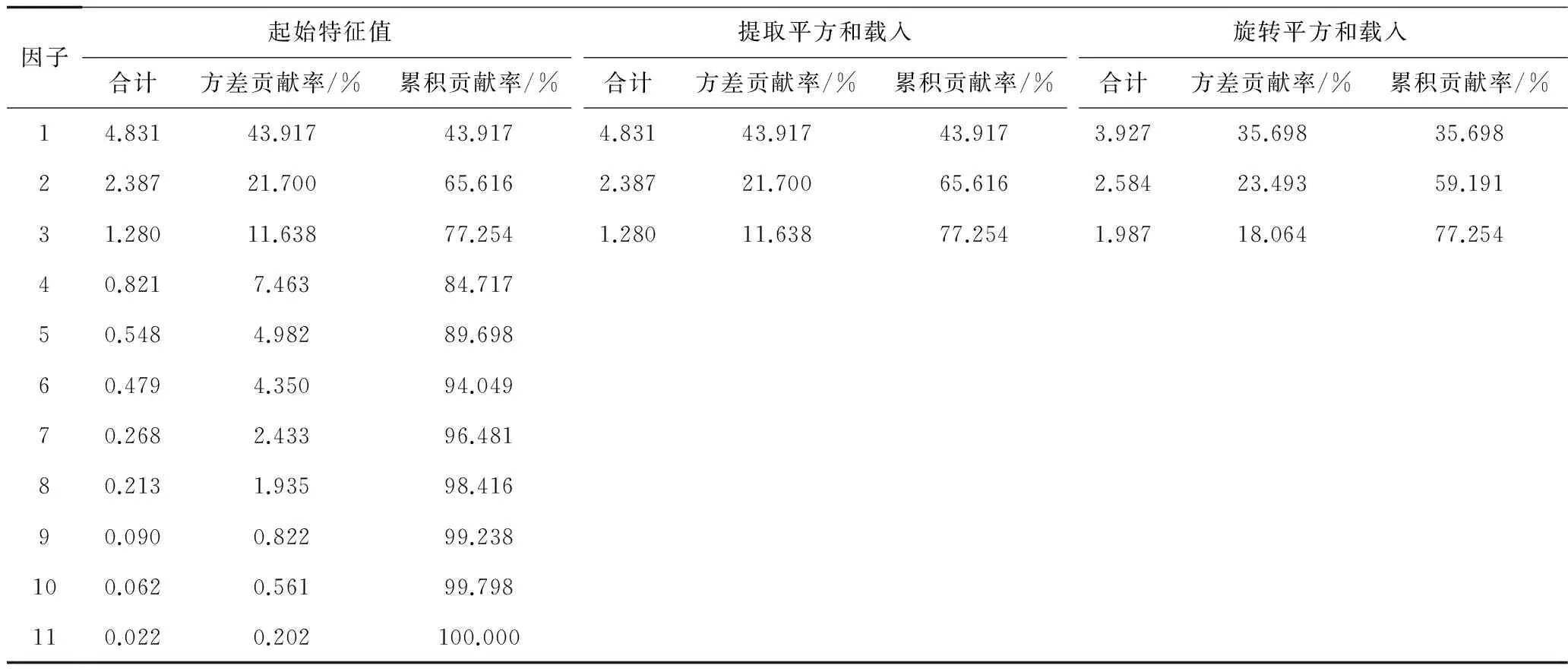
表4　特征值與方差貢獻率Table 4　Eigenvalues and variances

由表4可以看出，接地速度大、平飄距離長、接地點靠后、著陸減速慢、接地點靠前在第一個公因子上具有較高的載荷，這幾個因子主要是由于飛行速度控制弱引起的，因此稱為“著陸速度控制弱”因子。著陸偏離航向、著陸坡度大、拉平晚、拉平前恒滾擺動在第二個公因子上具有較高的載荷，這幾個因子主要是與飛行時的平衡控制有關，因此稱為“著陸平衡控制弱”。著陸俯仰速率大、進跑道高度高主要是與飛行時的升降控制有關，因此稱為“著陸升降控制弱”因子。上述得出的公因子即可作為進場著陸階段的評價指標，指標重要度的排序即可按照公因子的貢獻率大小來確定。

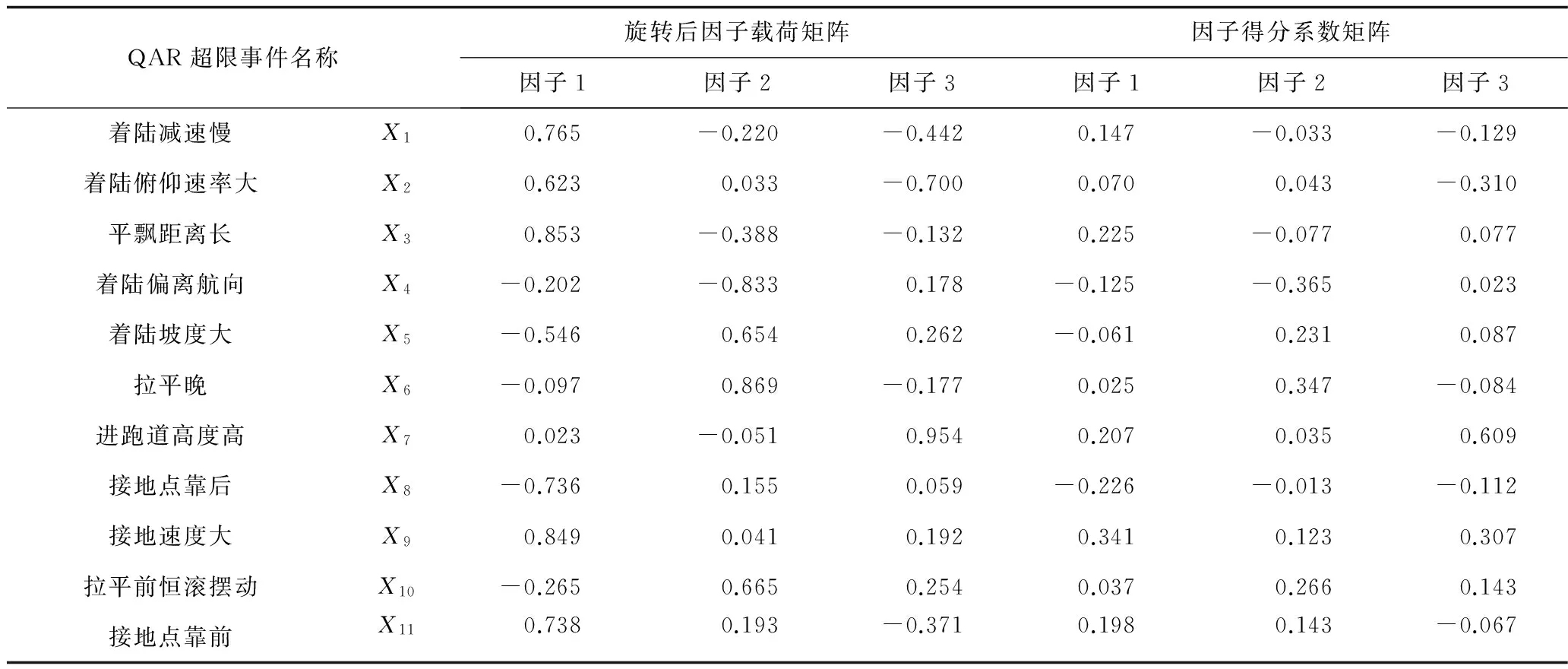
表5　旋轉后的因子載荷矩陣和因子得分系數矩陣Table 5　Rotated Component Matrix and Component Score Coefficient Matrix

2.2　構建飛行安全狀態評價突變模型

根據2.1中對進場著陸階段指標的確定方法，確定其他3個階段的評價指標，可得到飛行安全狀態的評價指標體系，如圖1所示。

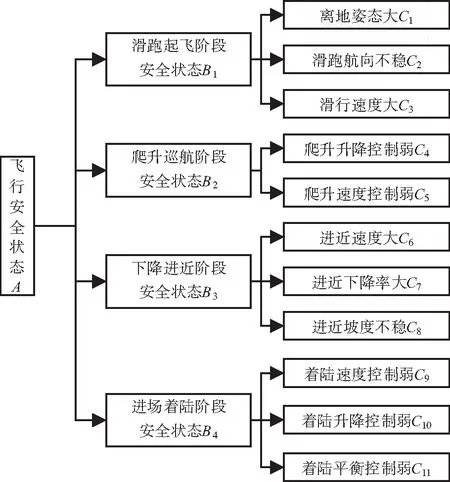
圖1　飛行安全狀態評價指標體系Fig.1　Evaluation index system of flight safety situation

據此，構建飛行安全狀態評價的突變模型，該模型分為2個層次。第1層次以飛行安全狀態作為狀態變量，以對應的滑跑起飛階段的安全狀態、爬升巡航階段的安全狀態、下降進近階段的安全狀態、進場著陸階段的安全狀態等一級指標作為控制變量。第2層次由4個子系統組成，每個子系統以1項一級指標作為狀態變量，以該一級指標對應的二級指標作為控制變量。

3　飛行安全狀態評價

模型建立后，利用該公司2015.01—2016.12(編號為01～24)的QAR數據，對該時期公司的飛行安全狀態進行評價。

3.1　確定評價指標的值

通過提取公因子，可以得到新的飛行安全狀態評價指標體系，但指標的值卻無法確定。可利用因子得分矩陣得到各公因子的得分表達式，算出得分作為新指標的值。進場著陸階段各公因子的得分表達式如下：

F1=0.147X1+0.070X2+0.225X3-0.125X4-0.061X5+0.025X6+0.207X7-0.226X8+0.341X9+0.037X10+0.198X11

(2)

F2=-0.033X1+0.043X2-0.077X3-0.365X4+0.231X5+0.347X6+0.035X7-0.013X8+0.123X9+0.266X10+0.143X11

(3)

F3=-0.129X1-0.310X2+0.077X3+0.023X4+0.087X5-0.084X6+0.609X7-0.112X8+0.307X9+0.143X10-0.067X11

(4)

同理可得到其他飛行階段各公因子的得分表達式，以2015年1月份的數據為例，將其代入到各公因子的得分表達式中，可得每個公因子的得分值，即指標的值，如表6所示。

表6　2015年1月份飛行安全狀態評價指標的值Table 6　The values of the flight safety situationevaluation indexs in January 2015

對上述所得的指標值進行標準化處理。設xi為第i項指標數值，xi′為其標準化值。在本文中，所有的指標均為逆向指標，指標值的標準化公式為：

(5)

式中：xi,max，xi,min分別指第i項指標的最大值與最小值。

3.2　計算安全評價隸屬值

由前面已知，滑跑起飛階段安全狀態、下降進近階段安全狀態、進場著陸階段安全狀態及其下一層指標均構成燕尾突變系統，爬升巡航安全狀態及其下一層指標構成尖點突變系統。同一狀態變量對應的控制變量之間均遵循互補原則。因此，各個階段的突變隸屬函數值分別為：

(6)

(7)

(8)

(9)

據統計，在世界民航1991—2000 年運輸飛行事故中, 起飛階段發生飛行事故占17%，著陸階段高達51%[17]。據此可劃分一級指標的重要度順序依次為進場著陸階段安全狀態B4、滑跑起飛階段安全狀態B1、下降進近階段安全狀態B3、爬升巡航階段安全狀態B2。該評價體系為蝴蝶突變系統，各指標之間遵循互補原則，可得到飛行安全狀態評價的突變隸屬函數值為：

(10)

同理可得到2015—2016年所有其他月份飛行安全狀態的評價值，如表7所示。

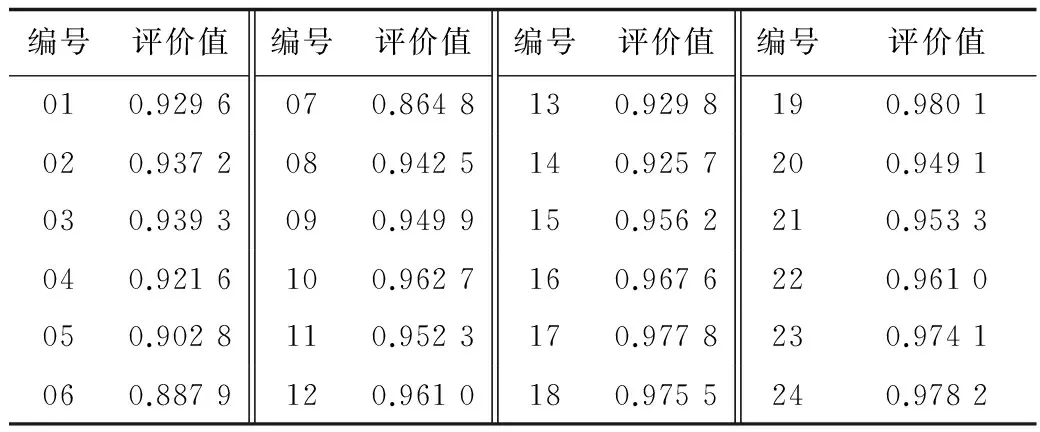
表7　2015—2016年度某航空公司A320機隊飛行安全狀態評價值Table 7　The values of flight safety situation evaluationfor a certain airline’s A320 fleet in 2015—2016

3.3　評價結果的分析

從表7可以看出，所得的評價值均接近于1，且各評價值之間的差值很小。這是由突變級數法中使用的歸一化公式造成的[18]。這一特點導致無法直接根據評價值對各月的飛行安全狀態進行比較和分析。為了對各月的飛行安全狀態進行區分和比較，需要確定評語集以及其對應隸屬度值的范圍。

結合公司運行的實際情況，將飛行安全狀態分為4個等級：Ⅰ級(較差)、Ⅱ級(一般)、Ⅲ級(好)、Ⅳ級(優)。各等級總隸屬度取值范圍的確定方法為：將指標體系中的最底層指標C1～C11賦相同的端點值，代入模型中進行歸一化運算，得到的總隸屬度值即為各等級劃分的臨界值。具體結果如表8所示。

根據表8給出的安全狀態評價等級，對該公司2015—2016年度的飛行安全進行分析。2015年1月—5月，公司的飛行安全處于一般狀態。6月、7月由于受雷雨和大風等惡劣天氣影響，公司的飛行安全狀態出現惡化。隨后，公司及相關部門采取了一系列的措施，包括對機組進行安全培訓，發布安全提示等，安全狀態得到好轉和提升。進入2016年以來，1月、2月由于公司開辟了多條北方新航線，受飛行員思想麻痹、航線保障不足等影響，飛行安全狀態有所下降。3月開始，公司作為試點開始推行安全績效管理，將安全關口前移，取得了良好效果。由此可見，評價結果與該公司A320機隊實際運行情況基本一致。從評價中可以得出，該公司的飛行安全狀態具有一定的波動性，飛行安全狀態的穩定和提高需要實施持續的安全管理手段。

表8　飛行安全狀態評價等級標準Table 8　Grade standard for flight safety situation evaluation

4　結論

1)運用因子分析法對QAR三級事件進行公因子提取，建立了包括滑跑起飛階段安全狀態、爬升巡航階段安全狀態、下降進近階段安全狀態、進場著陸階段安全狀態等4項一級指標以及離地姿勢大、爬升升降控制弱、進近速度大、著陸平衡控制弱等11項二級指標的飛行安全狀態評價指標體系。引入了突變級數法，構建出基于因子分析法與突變級數法的飛行安全狀態評價模型。

2)統計某航空公司2015—2016年24個月的QAR數據，采用該模型對公司的飛行安全狀態進行評價。所得的評價結果與該公司的實際運行情況相符，說明該模型具有較好的正確性和實用性。可以為飛行安全的評價及管理提供了一種新的思路。

[1]LIOUA J J H, TZENGB G H, CHANGA H C. Airline safety measurement using a hybrid model[J]. Journal of Air Transport Management, 2007, 13(4):243-249.

[2]AHMADI A, SODERHOLM P. Assessment of Operational Consequences of Aircraft Failures:Using Event Tree Analysis[J]. 2008, 76(4):1-14.

[3]唐衛貞. 基于物元模型的航空公司飛行安全風險綜合評價[J]. 安全與環境學報, 2015, 15(2):25-29.

TANG Weizhen. Comprehensive evaluation for the airline flight safety risk based on the matter-elements model [J]. Journal of Safety & Environment, 2015, 15(2):25-29.

[4]陳可嘉, 金煉. 航空公司飛行安全灰色區間層次評價[J]. 中國安全科學學報, 2015, 25(8):146-151.

CHEN Kejia, JIN Lian. Grey interval hierarchy evaluation of airline flight safety performance [J]. China Safety Science Journal, 2015, 25(8):146-151.

[5]JAVENSIUS SEMBIRING, LUDWIG DREES, FLORIAN HOLZAPFEL. Extracting unmeasured parameters based on quick access recorder data using parameter-estimation method[C]//Aiaa Atmospheric Flight Mechanics,2013.

[6]WANG L, WU C, SUN R. An analysis of flight quick access recorder(QAR) data and its applications in preventing landing incidents[J]. Reliability Engineering & System Safety, 2014(127):86-96.

[7]高揚, 王向章. 基于SPA-Markov的飛行安全態勢評估與預測研究[J]. 中國安全生產科學技術, 2016, 12(8):87-91.

GAO Yang, WANG Xiangzhang. Research on assessment and prediction of flight safety situation based on SPA-Markov [J]. Journal of Safety Science & Technology, 2016, 12(8):87-91.

[8]周長春, 胡棟棟. 基于灰色聚類方法的航空公司飛機進近著陸階段安全性評估[J]. 中國安全生產科學技術, 2012, 8(7):99-102.

ZHOU Changchun, HU Dongdong. Safety assessment of aircraft during approach-landing stage based on grey clustering method [J]. Journal of Safety Science & Technology, 2012, 8(7):99-102.

[9]甘旭升, 端木京順, 高建國. 基于相關向量機的飛行安全評價方法[J]. 中國安全生產科學技術, 2012, 8(12):143-148.

GAN Xusheng, DUANMU Jingshun, GAO Jianguo. Flight safety evaluation method based on relevance vector machine [J]. Journal of Safety Science & Technology, 2012, 8(12):143-148.

[10]劉得一，張兆寧，楊新涅. 民航概論[M]. 北京：中國民航出版社, 2011.

[11]WANG W, LIU S, ZHANG S, et al. Assessment of a model of pollution disaster in near-shore coastal waters based on catastrophe theory[J]. Ecological Modelling, 2011, 222(2):307-312.

[12]金佩劍, 王恩元, 劉曉斐,等. 沖擊地壓危險性綜合評價的突變級數法研究[J]. 采礦與安全工程學報, 2013, 30(2):256-261.

JIN Peijian, WANG Enyuan, LIU Xiaofei, et al. Catastrophe progression method on comprehensive evaluation of rock burst [J]. Journal of Mining & Safety Engineering,2013, 30(2):256-261.

[13]郭云濤, 賈永, 白思俊. 基于突變級數法的科技園區項目選擇決策研究[J]. 科技管理研究, 2017, 37(5):164-169.

GUO Yuntao, JIA Yong, BAI Sijun. Project selection of science and technology park based on catastrophe progression method [J].Science and Technology Management Research, 2017, 37(5):164-169.

[14]THOM R, FOWLER D H. Structural stability and morphogenesis:An outline of a general theory of models.[M]. London：Benjamin, 1975.

[15]周紹江. 突變理論在環境影響評價中的應用[J]. 人民長江, 2003, 34(2):52-54.

ZHOU Shaojiang. Application of catastrophe theory in environmental impact assessment[J]. Yangtze River, 2003, 34(2):52-54.

[16]駱方, 劉紅云, 黃崑. SPSS數據統計與分析[M]. 北京：清華大學出版社, 2011.

[17]趙鵬, 倪文, 韓峰. 如何預防飛行過程中的不安全因素[J]. 中國安全科學學報, 2006, 16(4):57-61.

ZHAO Peng, NI Wen, HAN Feng. How to prevent unsafe factors during flight [J]. China Safety Science Journal, 2006, 16(4):57-61.

[18]施玉群, 劉亞蓮, 何金平. 關于突變評價法幾個問題的進一步研究[J]. 武漢大學學報(工學版), 2003, 36(4):132-136.

SHI Yuqun, LIU Yalian, HE Jinping. Further study on some questions of catastrophe evaluation method [J]. Journal of Wuhan University of Hydraulic & Electric Engineering, 2003, 36(4):132-136.