基于ε-SVR的風篩式清選裝置清選性能預測研究

梁振偉，李耀明，周　全，馬　征，魏純才，王建鵬

(江蘇大學 現代農業裝備與技術教育部重點實驗室，江蘇 鎮江　212013)

0　引言

收獲機械的清選性能評價是多目標、多層次、多因素的，評價關系是模糊非線性的，至今沒有一種統一的確定預測模型。以往建立的關于清選預測模型主要運用回歸分析法[1]及人工神經網絡法[2]等，都是基于傳統的經驗風險最小化原則(ERM)，對于大樣本能給出較好的結果；但傳統的試驗研究需要耗費相當多的人力物力，同時在具有小樣本的清選性能預測中，ERM原則并不能保證期望預測風險最小化。為此，擬借助在統計學習理論的基礎上發展的分支支持向量機(Support Vector Machine，SVM)建立精度高、泛化能力強、隨機波動性小的清選性能預測模型。

支持向量機方法屬于機器學習理論發展的最新階段，首先是著眼于解決分類(模式識別)問題，通過引入不敏感損失函數ε的概念,也可以解決線性與非線性函數的回歸問題[3]。SVM的核心是基于VC維理論和結構風險最小化的原則，優點是可專門針對有限樣本，其目標是得到現有信息下的最優解，算法最終轉化為一個對偶尋優問題，得到的將是全局最優解。它避免了人工神經網絡等方法的網絡樣本需求大、結構選擇、過學習和欠學習、局部極小等問題。

以油菜聯合收獲機的清選裝置為研究對象，運用支持向量模型,描述其清選性能輸出與多個清選參數輸入之間的關系，具有算法復雜度與樣本維數無關等優點[4]。因此，探討將支持向量機理論引入清選裝置的清選性能研究中具有重要意義。

1　支持向量機的理論基礎

支持向量機訓練的實質為求解一個帶有界約束和線性等式約束的凸二次規劃問題。首先，通過非線性變換將輸入空間變換到一個高維空間，甚至是一個無限維空間；然后，在這個高維空間求解。其中，非線性變換是通過核函數K的方法來實現的。選取SVM模型ε-Support Vector Regression (ε-SVR)，給出一系列樣本數據點，即{(x1,z1),…,(xi,zi)}。其中，xi∈Rn為n維的輸入向量，而zi∈R1為輸出向量。標準的支持向量機的回歸模型由Vapnik于1995年提出[5]，即

其中

Qij=K(xi,xj)≡φ(xi)Τφ(xj)

式中ω—函數系數；

C—懲罰參數；

ε—不敏感損失函數；

該模型等價于

近似的回歸模型可以表示為

2　清選試驗

2.1試驗裝置

油菜脫出物清選試驗是在DF-1.5型物料清選仿真與控制裝置上進行的，試驗裝置的結構簡圖如圖1所示。

清選裝置采用風篩式的結構，主要由離心風機、振動篩、機架、傳動系統和傳感器等組成。離心風機、振動篩分別由調速電機驅動，轉速可以無級調節。試驗臺由曲柄連桿機構帶動篩箱運動，曲柄為偏心輪型，通過曲柄半徑的調節來實現篩箱振幅的變化。

2.2試驗材料

清選試驗使用的物料是油菜脫出混合物，主要成分為果莢殼、籽粒、短莖稈及輕雜質。為盡可能接近田間收獲狀態，所用物料都是剛從田間收割后經脫粒的脫出物，各成分所占比例為：果莢殼50%～53%，籽粒32%～34%，短莖稈8%～10%，輕雜質6%～8%。

2.3試驗方案與結果

通過對風篩式清選裝置清選機構及試驗條件的分析，選擇曲柄半徑、曲柄轉速、風機轉速、出風口傾角、篩孔直徑作為試驗因素，分別用A、B、C、D、E表示。試驗主要考察清選參數對清選效果H(包括清選含雜率F和清選損失率G)的影響，結合清選參數的最優值，每個參數設定3個水平數值，按照正交表L27(313)開展正交試驗，試驗方案及結果如表1所示。

為了研究樣本容量大小對ε-SVR預測模型的影響并與BP模型進行比較，試驗次數較多。在保證模型有意義的前提下，并不需要測定27組，可適當減小樣本容量。

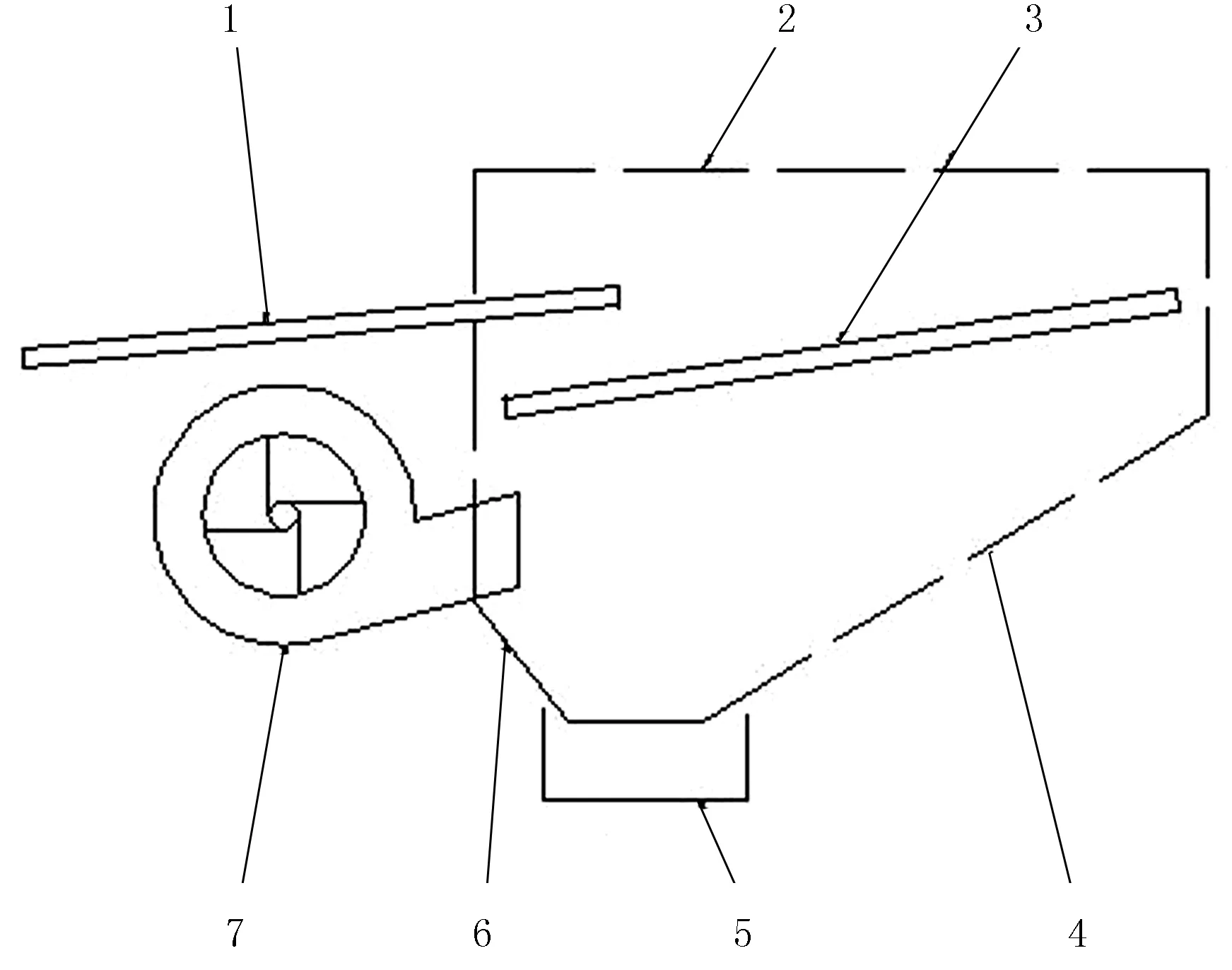
1.抖動板　2.罩殼3.振動篩　4.后滑板 5.集糧箱　6.前滑板　7.離心風機

序號因素A/mmB/r·min-1C/r·min-1D/(°)E/mm結果F/%G/%H/%1222608202062．24．483．1122222858602561．95．303．3603223109003061．457．533．8824262608603062．655．653．8145262859002061．754．852．9906263108202562．25．313．4507302609002562．56．644．1568302858203062．055．523．4389303108602061．67．063．78410222608202081．751．471．68311222858602581．752．341．986

續表1

3　參數建模

3.1模型的建立

由表1可知：試驗有2個因變量F和G。采用權重系數法可將兩個因變量轉化為單個因變量H=t1F+t2G。根據經驗以及經濟效益，取權重系數t1=0.6,t2=0.4。在ε-SVR模型中,將總樣本分為訓練樣本和測試樣本兩類。訓練時以A、B、C、D、E作為輸入，期望輸出是對應H值。

采用支持向量機建立預測模型必須先選擇合適的核函數。采用RBF(Radial Basic Function)核函數往往能夠得到較好的擬合結果，且收斂速度較快，核參數g主要影響樣本數據在高維特征空間中分布的復雜程度[6-7]。在訓練數據前，先對原始樣本進行數據規格化，并記錄在相應的映射關系中，縮放范圍為[0，1]；在訓練完畢后，對需要預測的數據再進行反歸一化。縮放的目的主要是在核計算中，會用到內積運算或exp運算，不平衡的數據可能造成計算困難。

3.2回歸預測ε-SVR參數ε、c、g的選擇

ε-SVR算法的參數是指在求解對偶問題時需要預先設定的參數，包括懲罰參數c、不敏感損失函數ε及核參數g。ε-SVR模型中的參數基于交叉驗證(Cross Validation，CV)的意義下尋參，常見的CV的方法有Hold-Out Method、 LOO-CV和K-CV等。第1種方法將原始數據隨機分成兩組，不能交叉驗證；第2種方法集合所有樣本用于訓練模型，計算成本較高；第3種方法能避免“過學習”以及“欠學習”狀態，K均分的組數一般大于等于2(標準K=10)。

采用CV方法進行參數優化的整體思路是：讓c和g在一定范圍內取值，對于取定的參數值，將訓練集作為原始數據集，利用K-CV方法得到此組c和g下訓練集驗證均方誤差MSE(Mean Squared Error)，最終取使得訓練集驗證MSE低的一組c和g的取值作為最佳參數。

在CV意義下，用非啟發式的網格劃分(GridSearch Method)尋找最佳c和g值能搜索到全局最優解；但在參數較多或取值范圍較大時，采用GA或PSO等啟發式算法，CV意義下的MSE作為適應度函數。啟發式算法不要求目標函數的凸性和目標的可微性，可以不必遍歷格內的所有參數點，也能找到全局最優解。GA和PSO優化和初始值選取有關，每次優化的數值是上下浮動的，結果取其平均值。

不同模型清選性能比較如表2所示，清選性能預測對比如表3所示。表2和表3采用表1中1～25組的試驗數據為訓練集，其余26～27組為測試集，分別采用了BP神經網絡、grid(cg)、ga(cg)和pso(cg)方法進行清選性能預測模型對比。利用GridSearch方法時，設定ε為定值，粗略估計c和g參數的范圍分別為2-20～220，粗略選擇的bestc=602 248.763 1，bestg=0.001 286，得到粗略選擇的等高線圖如圖2所示。

表2　不同模型清選性能比較

表3　清選性能預測結果對比

圖2　粗略選擇對應的等高線圖

MSE取值范圍約為0.48～1e-007，1e-007對應的c和g值較佳，可以縮小參數的選擇范圍。1e-007主要集中在兩個區域：c為2-2～210，g為22～210，c為2-2～210，g為2-5～23。其中，預測性能較好的為第1組，取其精細選擇的參數建立相應的模型bestc=0.770 711,bestg=4,ε=0.01。

采用ga(cg)方法的參數為：bestc=1.842 2，bestg=546.867 9，ε=0.01；采用pso(cg)方法的參數為bestc=2.094 6，bestg=650.330 1，ε=0.01。其中，終止代數為200，種群數量為20。

3.3BP和ε-SVR對應預測性能比較

BP神經網絡主體模型采用多層前饋網絡，其中隱藏層和輸出層的神經元數分別取為8和1，隱藏層和輸出層的激發函數分別設為tansig、purelin，訓練算法設為trainlm。

由表2可知：ga(cg)、pso(cg)訓練集模型的均方誤差比BP模型降低了2個數量級，比grid(cg)降低了接近2個數量級。與BP模型相比，ε-SVR模型的相關系數較高。其中，pso(cg)模型的相關系數最高，接近1。

表3給出了4種方法構造測試集的預測結果，將實際得到的清選性能值與模型輸出值進行對比，結果表明：ε-SVR預測性能優于BP預測。其中，ga(cg)和pso(cg)方法預測值的相對誤差比BP預測低1個數量級。

3.4樣本容量對ga(cg)預測性能的影響

一般認為，對于普通多元回歸，雖然在n≥k+1時就可以得到參數估計值(n為樣本容量，k為自變量的個數)，但為了提高參數估計量的有效性，應使n≥30或n≥2k(部分文獻要求n≥3k)，因此將不滿足這3個條件的一組樣本界定為小樣本[8]。以上述ga(cg)方法為例，建立相應的模型，選用RBF核函數來研究樣本容量大小對回歸預測精度的影響。圖3、圖4和圖5中選用第27組作為測試集，1-26組為訓練集。樣本容量n依次取8，10，…，24，26。對應的測試集的MSE值如圖3所示，不同樣本容量對應的BP和ga(cg)訓練模型MSE值如圖4所示，不同樣本容量大小對應的BP和ga(cg)預測值如圖5所示。

圖3　不同樣本容量大小對應的ga(cg)測試模型MSE值Fig.3　Test Set Regression MSE of samples in different by ga(cg)

圖4　不同樣本容量對應的BP和ga(cg)訓練模型MSE值Fig.4　Train Set Regression MSE of samples in different by ga(cg) and BP

圖5　不同樣本容量大小對應的BP和ga(cg)預測值

由圖3可知：MSE值隨著樣本容量的增加而遞減并逐漸向0逼近；在控制MSE值時，可根據實際適當減少試驗的次數，在試驗數據缺失較多時可采用ε-SVR的方法進行回歸預測。

由圖4可知：不同樣本容量大小對應ga(cg)方法訓練集模型的MSE值均顯著低于BP模型，訓練集模型對應的MSE值能維持在10-5，BP訓練集模型對應的MSE值隨樣本容量的增加波動較大。

由圖5可知：隨著樣本容量的增加，用ga(cg)方法得到的預測值能逐漸逼近真實值，且預測值較穩定；用BP方法得到的預測值并不穩定，且隨機性較強。

4　結論

1)基于非啟發式GridSearch 方法尋求SVR模型最佳參數c和g時，采用等高線圖的方式表達，更具直觀性；啟發式GA和PSO尋優預測精度更高，能有效避免憑經驗選取參數的隨機性和BP的結構性選擇。

2)采用支持向量機能較好地描述多個參數對清選性能的影響，所得預測數值穩定性更強，預測精度更高，能適應“小樣本、貧信息”的數據分析，具有良好的工程應用價值。

參考文獻：

[1]夏利利,李耀明,徐立章.二次響應曲面模型在聯合收割機清選氣流場預測中的應用[J].農機化研究,2009，31(2) :125-127.

[2]李耀明,林恒善,陳進,等.基于神經網絡的風篩式清選氣流場研究[J].農業機械學報,2006,37(7) :197-198.

[3]Gunn S R. Support vector machine for classification and regression[R]. Southampton, UK:ISIS-1-18, University of Southampton,1998.

[4]陳永義,俞小鼎,高學浩,等.處理非線性分類和回歸問題的一種新方法(I)—支持向量機簡介[J].應用氣象學報,2004,15(3):345-354.

[5]Vapnik V N. The nature of statistical learning theory[M]. New York: Springer-Verlag,1995.

[6]張曉東,毛罕平,陳秀花.基于PCA-SVR的油菜氮素光譜特征定量分析模型[J].農業機械學報,2009,40(4):161-165.

[7]李盼池,許少華.支持向量機在模式識別中的核函數特性分析[J].計算機工程與設計,2005,26(2):302-304.

ID:1003-188X(2018)04-0026-EA