古典概型學習直通車

古典概型是高考考查的重點和熱點,考查的主要內容是事件發生的概率的求解,且常與其他相關知識交匯命題。那么什么是古典概型?古典概型的概率該如何計算呢?下面就讓我們一起登上古典概型學習的直通車吧!

一、知識要點梳理

1.古典概型。

(1)定義：一個試驗滿足以下兩個特征：①有限性：試驗的所有可能結果只有有限個,每次試驗只出現其中的一個結果。②等可能性：每一個試驗結果出現的可能性相等。我們把具有這兩個特征的隨機試驗的數學模型稱為古典概型(古典概率模型)。

(2)計算公式：對于古典概型,通常試驗中的某一事件A是由幾個基本事件組成的。如果試驗的所有可能結果(基本事件)的總數為n,隨機事件A包含的基本事件的個數為m,那么事件A的概率規定為

(3)求古典概型概率的步驟：①反復閱讀題目,收集題目中的各種信息,理解題意;②判斷試驗是不是等可能事件,并用字母表示所求事件;③利用列舉法或其他方法計算基本事件的總數n及事件A包含的基本事件的個數m;④計算事件A的概率

2.建立概率模型。

(1)一般來說,在建立概率模型時,一個基本事件(即一個試驗結果)是人為規定的,每次試驗有且只有一個基本事件出現。只要基本事件的個數是有限的,并且它們的發生是等可能的,那么這種概率模型就是古典概型。

(2)對于同一個隨機試驗,可以根據需要建立滿足要求的概率模型。

(3)從不同的角度去考慮一個實際問題,可以將問題轉化為不同的古典概型來解決,而所得到的古典概型的所有可能結果數越少,問題的解決就會越簡單。

二、重要題型導學

1.基本事件的個數判斷。

例1一口袋內裝有大小相等的1個白球和已編有號碼的3個黑球,從中摸出2個球。

(1)共有多少種不同的結果(基本事件)?

(2)摸出2個黑球有多少種不同的結果?

思路分析：由題目可獲取以下主要信息：口袋內的4個球是有區別的,摸出其中任意2個球都是一種結果,要把各種情況一一列舉出來。

解：(1)基本事件共有6種不同的結果,分別為(黑1,黑2),(黑1,黑3),(黑2,黑3),(白,黑1),(白,黑2),(白,黑3)。

(2)從上面所有結果可看出摸出2個黑球的結果有3種。

評注:基本事件個數的探求方法:①列舉法,此法適合于較簡單的試驗。②樹狀圖法,樹狀圖也是列舉的一種常用方法,適合較復雜問題中基本事件個數的探求。

2.古典概型的判斷。

例2一口袋中有大小相同的5個白球、3個黑球和3個紅球,每個球都有一個區別于其他球的編號,從中摸出1個球。

(1)有多少種不同的摸法?如果把每個球的編號看成是一個基本事件的概率模型,則該模型是不是古典概型?

(2)若將球的顏色作為基本事件,則有多少個基本事件?以這些基本事件建立概率模型,該模型是不是古典概型?

思路分析：由題目可獲取以下主要信息：①袋中有大小相同的5個白球、3個黑球和3個紅球。②每個球都有一個區別于其他球的編號,現從中摸出1個球。解答本題可先確立概率模型,以及它是由哪些基本事件所構成的,然后再判斷該模型是否滿足古典概型的特點,進而確定是不是古典概型。

解：(1)由于共有11個球且每個球都有不同的編號,故共有11種不同的摸法。又因為所有球的大小相同,因此每個球被摸中的可能性相等,故以球的編號為基本事件的概率模型為古典概型。

(2)由于11個球共有3種顏色,因此共有3個基本事件,分別記為：A：“摸到白球”,B：“摸到黑球”,C：“摸到紅球”。又因為所有球的大小相同,所以一次摸球時每個球被摸中的可能性均為,而白球有5個,故一次摸球時摸中白球的可能性為。同理可知,摸中黑球、紅球的可能性均為。顯然這3個基本事件出現的可能性不相等,所以以顏色為基本事件的概率模型不是古典概型。

評注:針對這個類型的題目,首先要看這個概率模型是由哪些基本事件構成的,然后再研究這些基本事件的個數是否有限、出現的可能性是否相等。要注意的是選擇的基本事件不同,結果可能有所不同。

聯盟共舉辦兩屆“基于HIM的廣義BIM矩陣(GIM)論壇”、兩屆“中國BIM經理高峰論壇”，第一屆全國建筑業“互聯網+”技術展示會，2016建筑施工BIM應用項目觀摩會，參展“第十三屆國際綠色建筑與建筑節能大會暨新技術與產品博覽會”，協辦“buildingSMART 2017年香港國際BIM大賽暨高峰論壇”，協辦第四屆BIM國際技術交流會等，通過論壇展覽展示活動不斷擴大聯盟影響力。

3.列舉法求古典概型的概率。

例3一口袋中有6個球,其中4個白球,2個紅球,從袋中任意取出2個球,求下列事件的概率：

(1)事件A：取出的2個球都是白球。

(2)事件B：取出的2個球中1個是白球,1個是紅球。

思路分析：先將基本事件一一列出,并加以計數,再用古典概型的概率計算公式求解。

解：設4個白球的編號為1,2,3,4,2個紅球的編號為5,6。從袋中的6個球中任取2個球的取法有(1,2),(1,3),(1,4),(1,5), (1,6),(2,3),(2,4),(2,5),(2,6),(3,4), (3,5),(3,6),(4,5),(4,6),(5,6),共15種。

(2)從袋中的6個球中任取2個球,其中1個是白球,1個是紅球,其取法包括(1,5), (1,6),(2,5),(2,6),(3,5),(3,6),(4,5), (4,6),共8種。所以取出的2個球中1個是白球,1個是紅球的概率為

評注:①列舉法可以使我們明確基本事件的構成,該法適合于基本事件的個數比較少的情況。②列舉時要按規律進行,通常采用分類的方法列舉,這樣可以避免重復或遺漏。

4.圖表法求古典概型的概率。

例 4漢字是世界上最古老的文字之一,字形結構體現著人類追求“均衡對稱、和諧穩定”的天性。如“土”“口”“木”三個漢字,均可以看成是軸對稱圖形。

(1)請再寫出兩個可看成是軸對稱圖形的漢字。

(2)小敏和小慧利用“土”“口”“木”三個漢字設計一個游戲,規則如下：將這三個漢字分別寫在背面都相同的三張卡片上,背面朝上,洗勻后先抽出一張,放回洗勻后再抽出一張,若兩次抽出的漢字能組成上下結構的漢字(如“土”“土”組成“圭”),則小敏獲勝,否則小慧獲勝。你認為這個游戲對誰有利?請用列表的方法進行分析,并說明寫出組成的漢字。

思路分析：可以先用列表法列出所有可能的結果,再用古典概型的概率計算公式求解。

解：(1)如田,日,王等。

(2)這個游戲對小慧有利。每次游戲時,所有可能出現的結果如表1所示。

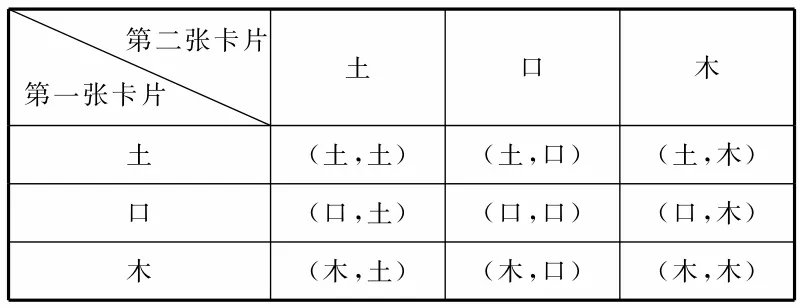
表1

由表1可知共有9種結果,且每種結果出現的可能性相等,其中能組成上下結構的漢字的結果有4種：(土,土)組成“圭”,(口,口)組成“呂”,(木,口)組成“杏”或“呆”,(口,木)組成“呆”或“杏”。所以小敏獲勝的概率為,可知小慧獲勝的概率為。故這個游戲對小慧有利。

評注:在求古典概型的概率時,通常先將總的基本事件用表格或直角坐標系中的點表示,以方便我們更直接、更準確地找出某個事件所包含的基本事件的個數,然后再根據古典概型的概率計算公式求出相應的概率。

5.樹狀圖法求古典概型的概率。

例5甲口袋中裝有2個相同的小球,它們的標號分別為2和7;乙口袋中裝有2個相同的小球,它們的標號分別為4和5;丙口袋中裝有3個相同的小球,它們的標號分別為3,8,9。從這3個口袋中各隨機地取出1個小球。

(1)求取出的3個小球的標號全是奇數的概率。

(2)以取出的3個小球的標號分別表示3條線段的長度,求這些線段能構成三角形的概率。

思路分析：讀懂題意,利用樹狀圖列出所有可能情況。

解：(1)畫出樹狀圖,如圖1所示。

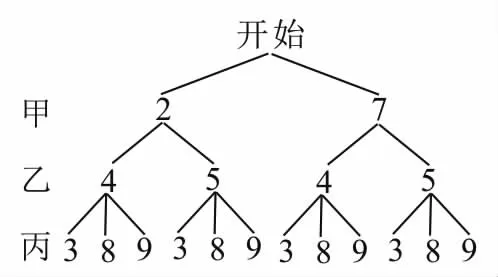
圖1

由圖1可知共有12種等可能的結果。取出的3個小球的標號全是奇數的情況有(7,5,3),(7,5,9),共2種,所以所求概率為

(2)由圖1可知這些線段能構成三角形的有(2,4,3),(7,4,8),(7,4,9),(7,5,3), (7,5,8),(7,5,9),共6種情況,所以所求概率為

評注:畫出樹狀圖,用列舉法表示等可能的有限個試驗結果,可以直觀地理解題意,尋找解題思路。

三、易錯點剖析

例6一對年輕夫婦喜得雙胞胎,請問雙胞胎中一男一女的概率是多少。

錯解：雙胞胎有雙男、雙女、一男一女共3個基本事件。設事件“一男一女”為A。

因為n=3,k=1,故一男一女的概率

剖析：以上3個基本事件不是等可能的。實際上,按出生時間先后,雙男有(男,男)這1種,雙女有(女,女)這1種,而一男一女有(男,女),(女,男)這2種。等可能事件要抓住“等可能”這個實質,“等可能”重在結果,而不是事件本身。

正解：雙胞胎的性別按出生時間先后有(男,男),(女,女),(男,女),(女,男)這4個基本事件。設事件“一男一女”為A,則n=4,k=2,所以一男一女的概率

評注:求古典概型的概率應注意以下問題:①判斷是否具備有限性和等可能性這兩個特征,特別是等可能性。②由于觀察的角度不同,基本事件的個數就不同,因為基本事件的總數和事件A包含的基本事件的個數的計算必須站在同一角度。

四、實戰演練

1.從甲、乙、丙3人中任選2名代表,甲被選中的概率是( )。

2.一盒中有1個黑球和9個白球,它們除顏色不同外,其他方面沒有什么差別。現有10個人依次摸出1個球,設第1個人摸出的1個球是黑球的概率為P1,第10個人摸出黑球的概率是P10,則P1與P10的關系是____。

參考答案：

1.C2.P1=P10