超聲波綜合實驗裝置的設計與研制

彭國華,　熊永紅,2，　李泰強，　倪　昀，　丁　浩

(1.文華學院 基礎學部，武漢 430074；2.華中科技大學 物理學院，武漢 430074)

0　引　言

聲波是一種機械波，它可以在氣態、液態、固態物質中傳播。人耳能聽到的聲波頻率在0.02～20 kHz，超聲波在媒質中傳播時，聲速、聲衰減和聲阻抗都和媒質的特性及狀態有關，通過測量這些聲學量可以探知媒質的特性和狀態變化。這些聲學量的測量方法是超聲無損檢測、超聲雷達、超聲成像等實驗基礎。超聲波的特性和測量方法在科學研究、醫療診斷和治療、工業生產、日常生活等各方面都有廣泛應用。因此，研究超聲波的基本特性和測量方法有著非常重要的現實意義和價值。

本文結合湖北省大學生物理實驗創新設計競賽，研制了一種超聲波綜合實驗裝置，該裝置不僅可以完成超聲波速度的測量，還可以觀測和研究超聲波在傳播過程中的反射、透射、折射、布拉格衍射現象和規律，測量超聲波在不同材質中的折射率和模擬X射線衍射，測量“晶體模型”的晶格常數，測量超聲波在不同材質中的衰減情況。該項目2016年已經獲得第四屆光馳杯湖北省大學生物理實驗創新設計競賽一等獎。

1　裝置設計與研制

超聲波在介質中傳播具有反射、透射、吸收、折射、干涉和衍射等物理現象，在傳播過程中遇到障礙物，超聲波的傳播方向和聲強分布會發生改變。因此我們設計了一個基于精密測角儀、兩個相互垂直的線性測長儀、超聲波發射和接收系統等模塊，構建組合式超聲波綜合實驗裝置。將超聲波發射器和探測器分別固定在該裝置的發射架和測試架上，就可測量超聲波聲強在三維空間的分布。

該綜合實驗裝置框架由以下幾部分組成：超聲波發射系統、超聲波接收系統，超聲波測量系統、載物臺、實驗介質和超聲波元器件、信號源和示波器。

精密測角儀由底座、中心軸、游標盤和刻度盤構成，其結構如圖1所示。刻度盤采用圓形設計，游標采用半圓或圓弧設計，增大刻度盤和游標盤直徑，細分最小分度值，使角度測量的精度有所提高。超聲波發射器安裝在綜合裝置的發射架上，超聲波發射器在發射架上的高度可調。

圖1　超聲波綜合實驗裝置結構示意圖

超聲波接收器安裝在裝置的測試架上，超聲波接收器三維可調，在水平面繞中心軸左右轉動，可以進行樣品反射角、折射角或衍射角的精確測量；水平線性測長儀由主測量尺和游標構成，通過水平線性測長儀可以觀測超聲波的干涉現象，用共振干涉法或相位比較法測量超聲波的傳播速度；垂直線性測長儀的測量原理與水平線性測長儀原理相同，垂直線性測長儀與水平線性測長儀是正交結構，如圖1所示。通過垂直線性測長儀可以測量超聲波強度在垂直方向的分布。

水平測長儀與轉動平臺固定連接，與刻度盤和角游標共同構成精密測角儀。這樣，就可以實現超聲波某些性質的三維測量。

將該裝置與示波器和信號源連接，將測量介質置于載物臺上即可進行實驗數據的測量，通過觀察示波器波形幅值的強弱，記錄數據，經理論計算與分析即可得出結論。

2　實驗觀測

2.1　單縫衍射法求超聲波的波長

超聲波具有衍射的特性，當超聲波垂直入射單縫衍射模板后，在單縫后面便會出現超聲波的單縫衍射圖樣，即超聲波聲強出現強弱分布的現象，如圖2所示。

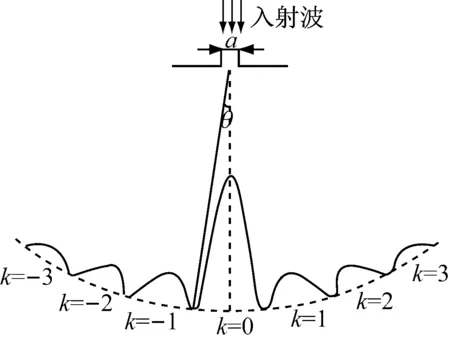
圖2超聲波單縫衍射示意圖

衍射圖樣中極小值對應的角度θ：

asinθ=kλ，k=1,2…

(1)

式中：a表示縫寬；k表示級次；θ是衍射超聲波束與單縫模板法線的夾角,稱為衍射角；λ表示超聲波的波長。

衍射強度隨超聲波接收端轉動角度變化，尋找波形峰值極小值點，即衍射強度最弱的位置，讀出接收裝置轉動的角度θ，將其代入式(1)即可算出超聲波的波長。將測量的波長與理論波長相比較即可求出實驗誤差。

2.2　布拉格衍射

實驗所用的測量樣品為簡單立方晶體模型，其結構就是一個三維光柵，超聲波通過該三維光柵就會產生布拉格衍射。當超聲波入射方向與某個晶面成一定夾角時，會產生光程差，當光程差等于波長的整數倍時，此時晶面的衍射分布就滿足布拉格方程:

(2)

式中：d為晶面間距。對于一個三維晶體模型，在水平方向上，可以利用精密測角儀準確測量出超聲波對應某個晶面的衍射角θ，代入式(2)即可算出晶面間距d，再將實驗測得的d測與模型的標稱值d標進行比較即可得出實驗誤差。同理，在豎直方向上通過豎直的測量尺和示波器找到滿足衍射極大值的位置，測出此方向的相對距離，再測量出兩超聲波壓電換能器探頭距離，利用三角函數算出θ，代入布拉格方程即可算出豎直方向上的晶面間距，對于第三維方向上的晶面間距，只需將晶體模型在水平方向上轉動90°重復上述實驗方法即可算出第三方向的晶面間距d。

圖3所示為布拉格衍射中的簡單立方結構晶體模型，晶面間距為21.00 mm。

圖3　簡單立方結構晶體模型示意圖

2.3　利用超聲波測量不同材料的折射率

不同材料對同一頻率的超聲波其折射率是不同的。通過自制泡沫材質的正三棱柱和PLA材質的正三棱柱作為待測樣品，用超聲波綜合實驗裝置對泡沫和塑料樣品的折射率進行測量。超聲波發射方向與三棱柱某一面成一定角度，慢慢轉動超聲波接收端，尋找示波器上幅值極大值點，找到極大值點后，記下刻度盤讀數，再將接收端轉到和發射端軸線平行的位置，記下刻度盤讀數，兩數相減即為最小偏向角δ，即可算出折射率n(三棱柱的頂角A=60°)，實驗原理如圖4所示。

(3)

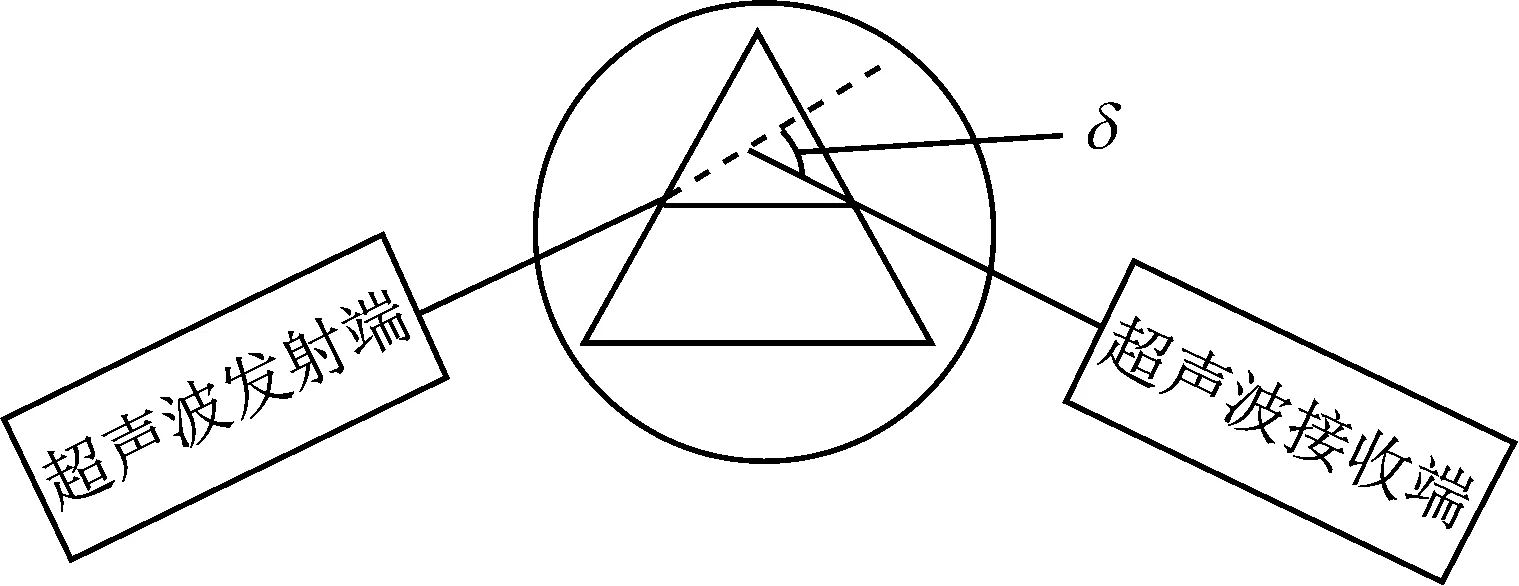
圖4超聲波折射率測量示意圖

3　實驗數據

3.1　單縫衍射法求超聲波波長

超聲速在空氣中的傳播速度與空氣中的濕度和環境的溫度有關，本次實驗在干燥下的環境下進行，室內溫度24 ℃。由超聲波在空氣中的傳播速度的理論值可由下式計算：

(4)

式中：v0為t=0 ℃時的聲速，v0=331.5 m/s；T為環境熱力學溫度。根據式(4)求出聲速vT，由速度與波長的關系可以算出超聲波的波長。由該式可以算出24 ℃下的聲速為345.76 m/s，實驗中超聲波換能器發射端的發射頻率為40.566 kHz，則由λ=v/f即可算出理論波長λ理=8.52 mm。

表1為單縫衍射法測超聲波波長的實驗數據，表中θ0為發射端超聲波換能器中心軸線與接收端超聲波換能器中心軸線共線時接收端所處的初始角度位置，為轉動接收端示波器出現極小值時接收端所處的角度位置，θ為衍射角，由以上數據可測出出現一級極小衍射測出λ1為8.53 mm，誤差為0.2%；二級極小衍射測出λ2為8.57 mm，誤差為0.6% 。

表1　單縫衍射法求超聲波波長數據表(a=25 mm)

3.2　布拉格衍射

布拉格衍射數據見表2、3。由布拉格方程(2)可知，求解模型的d需知超聲波長λ，取λ理=8.52 mm，為已知量。θ1實驗開始前超聲波發射端換能器中心軸線與接收端換能器中心軸線共線時初始角度θ0=251°50′。當轉動接收端觀察示波器第一次出現極大值時，記下θ極大，即可算出θ值，代入式(2)即可算出模型d測，d標為模型晶面間距的實際值，d測與d標相比即可算出相對誤差。

表2　布拉格衍射數據表(水平方向100)

表3　布拉格衍射數據表(豎直方向001)

表3為布拉格衍射在豎直方向上的數據表，本實驗用到的立方體模型是個三維模型，利用該裝置可以進行三維測量的特點進行實驗。先測量實驗開始前發射端與接收端中心軸線共線狀態下2個超聲波換能器探頭端面的距離l，同時記下接收端換能器在豎直游標上的初始位置d0，接著移動接收端，直到示波器第一次出現極大值，記下標尺讀數d1，則衍射角

θ=arctan[(d1-d0)/l]

將θ代入式(2)即可算出d測。

3.3　利用超聲波測量不同材料的折射率

為測不同材料的超聲波折射率，本實驗采用了兩種材料，三棱柱頂角均為60°，由式(3)計算材料折射率。在進行泡沫折射率的測量實驗中測得的超聲信號極大值的臨界角θ臨=202°，初始位置θ0讀數221°40′,則δmin=19°40′，算出泡沫的折射率為1.28。

同理，在進行PLA折射率的測量中測得θ臨=184°35′，θ0=218°40′，則δmin=34°5′，算出PLA的折射率為1.46。

4　分析討論

對于簡單立方晶體模型的水平和垂直方向的晶格常數測量存在明顯的誤差，通過對裝置的分析可知，問題主要出在衍射角度的測量上。水平測量采用的是精密測角儀，所以測量結果與標稱值對比誤差較小。而垂直測量衍射角存在較大的誤差，其原因如圖5所示。

圖中：a表示縫寬；D表示從狹縫到超聲波傳感器的距離。因衍射角度較小，可以假設：sinθ≈tanθ。

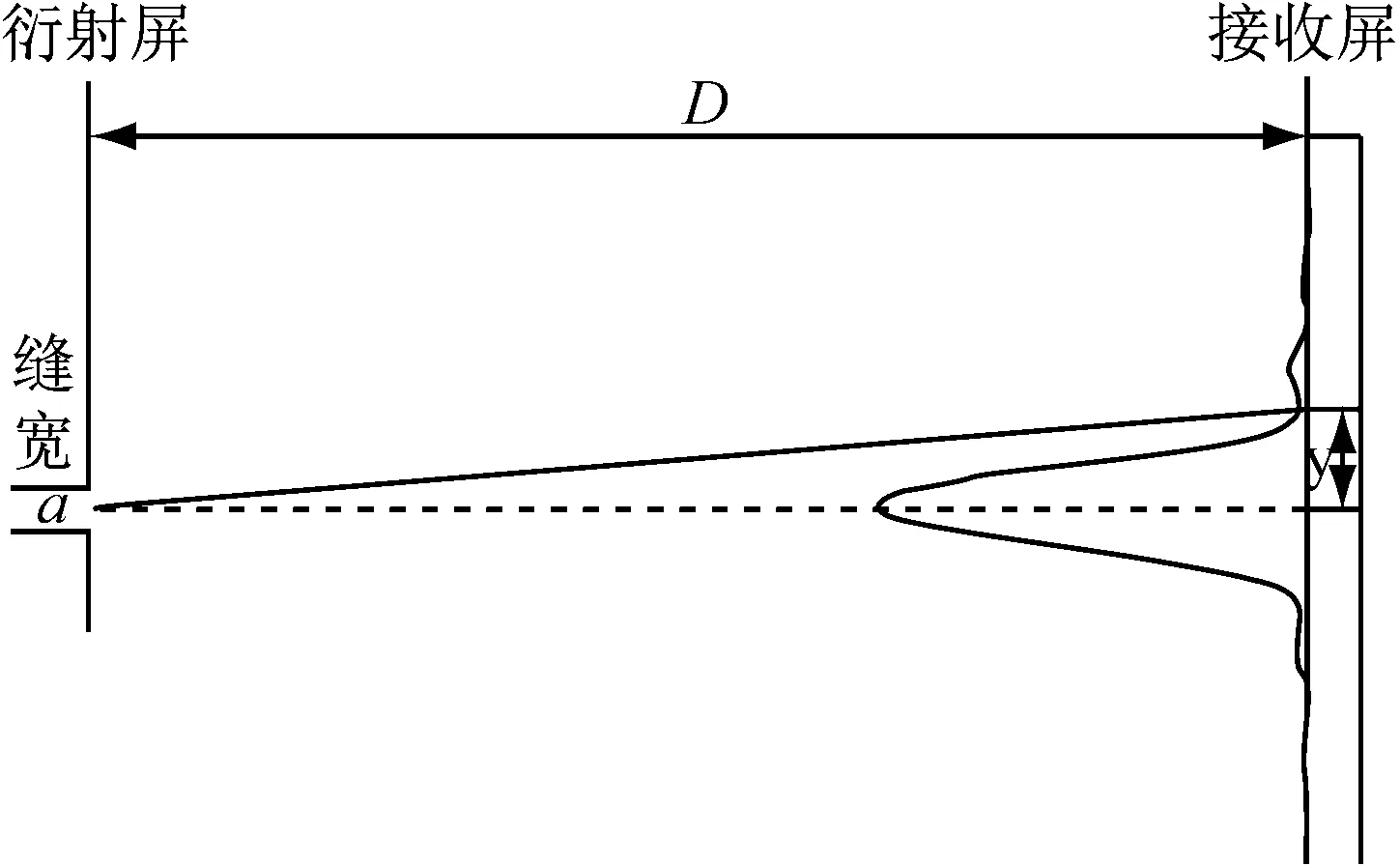
圖5垂直測量示意圖

根據三角關系有：

tanθ=y/D

(5)

a=kλD/y，k=1,2,…

(6)

正是由于sinθ≈tanθ這種三角關系的近似引入了實驗的誤差，使(001)方向的測量誤差大于(100)的測量誤差。通過將樣品(001)方向旋轉90°在水平方向進行測量，可使測量誤差降低。

5　結　語

晶體微結構尺度在10-10～10-8m的范圍，只有用SEM、STM、XRD等測量物質微結構的大型精密測量儀器，才能夠對物質的微結構進行測量、分析和研究。但這些大型精密儀器價格昂貴，XRD還有輻射源，對測量環境和實驗人員都有很高的要求，因此不可能用于本科生物理實驗教學。用超聲波實驗裝置對“晶體”模型進行測量，不僅讓我們能直接觀測 “晶體”結構，還可間接地學習XRD的測量原理，培養學生科學思維能力，學習用變量轉換法和物理模擬法來設計新實驗裝置，將看不見的微觀物理量轉換為看得見的幾何參量，用常規的超聲波發射器模擬X射線源，避免了X射線輻射。

利用超聲波綜合實驗裝置，不僅可以進行超聲波的反射、透射、折射、干涉和衍射等系列實驗研究內容。同學們還可以在該裝置上進行DIY實驗內容的拓展，進行創新設計和探索性實驗內容的研究。

參考文獻(References)：

[1]熊永紅，張昆實，任忠明，等.大學物理實驗(第一冊)[M].北京：科學出版社，2007：117-123.

[2]趙荒培. 鋼材中超聲波衍射的布拉格(Bragg)方程應用[J]. 物理測試,2014(5):59-62.

[3]王敏. 分光計最小偏向角法測量方案及其誤差產生原因與改進[J]. 電子測試,2014(2):39-40+9.

[4]王曉穎,王濤,李武軍. 超聲光柵實驗中聲致折射率變化的研究[J]. 大學物理,2012(5):50

[5]袁仁福. 超聲波技術的現狀和發展趨勢[J]. 世界科學,1993(1):35-39.

[6]呂令杰. 勻速運動介質中的聲波干涉[J]. 大學物理,2016(2):52-55.

[7]孫艷,于丹,王廣. 利用布拉格衍射模擬信號傳輸[J]. 科技信息,2010(6):113-114.

[8]何穎卓,李春芝. 微波布拉格衍射實驗中測量衍射極大值的新方法[J]. 大學物理實驗,2013(5):9-12.

[9]傅崧原. 一種水波聲波干涉實驗裝置[J]. 科技創新與應用,2013(36):55.

[10]劉戰存,苑紅霞. 布拉格父子對X射線晶體衍射的研究及其啟示[J]. 首都師范大學學報(自然科學版),2006(1):32-36.

[11]曹連振,劉霞,張瑩,等. 分光計測最小偏向角法內容的延伸及數據處理的改進研究[J]. 濰坊學院學報,2012(2):76-78.

[12]袁哲峰. 分光計測量三棱鏡折射率的誤差分析[J]. 科技資訊,2006(16):2-4.

[13]李昂,王建鋒,劉洋. 分光計測量三棱鏡頂角實驗的兩學時課堂教學探討[J]. 教育教學論壇,2014(38):248-249.

[14]鄔融,田玉婷,趙東峰，等. 透射衍射光柵內全反射級次[J]. 物理學報,2016(5):106-114.

[15]Kessler L. Ultrasonic visualization by pulsed bragg diffraction: U.S. Patent 3,737,573[P]. 1973-6-5.

[16]Santiago J G, Dutton J C. Velocity measurements of a jet injected into a supersonic crossflow[J]. Journal of Propulsion and Power, 1997, 13(2): 264-273.