不同分聯形式對山區不規則梁橋抗震性能的影響

狄秉臻

(西南交通大學土木工程學院，四川成都 610031)

隨著交通基礎設施建設不斷推進，在西部山區修建了越來越多的高速公路橋梁。因經濟性、施工周期等因素，主梁形式為T梁、小箱梁的梁橋仍占有很大比例。山區地勢起伏不定，但受限于截面形式，T梁橋或小箱梁橋的跨徑不大，一般在50 m以下，因此其難以一跨越過山溝坡地。這樣就導致需要在溝底及附近位置設置橋墩，同時也造就了山區梁橋的特點之一：最大墩高較大，各墩之間高差大。同時西部山區橋梁另一個特點是處于地震頻發區。我國地震呈“東弱西強”分布，在西部地區，7級及以上的強震發生的概率也較大，比如2008年的汶川地震，2013年的雅安地震[1]。因此山區橋梁在設計時，必須重視其抗震性能。

結合上述西部山區橋梁的兩個特點，采用簡支或短聯形式時，就會面臨以下幾種問題：(1)落梁的可能性大[2]。汶川地震中，廟子坪大橋、百花大橋和高原大橋等均發生落梁。在發生落梁后，因搶修難度大，交通一時難以恢復，會嚴重阻滯震后救援的進行。(2)整體性差，自振頻率低。各跨之間不能協同抗震，且橋梁結構頻率低、周期長，在地震作用下，會導致過大的變形，此時位移代替強度成為控制指標[3]。(3)伸縮縫數量多。有研究表明，伸縮縫兩端梁體相互碰撞，是導致落梁的主要原因之一，輕則也會造成兩端混凝土破碎[4]。(3)地震作用下，各墩之間內力分布不均[5]。在截面相同時，高墩相對矮墩剛度小，矮墩過大的剛度會導致其承擔較大的內力，這樣顯然是不利的。當采用長聯形式時，上述問題理論上可得到改善，因此本文對比了長短聯形式下橋梁結構的地震響應，以提出更適合于山區橋梁的分聯形式。

1 模型參數

使用MIDAS/CIVIL軟件建立了6×40 m預應力混凝土連續T梁橋模型，如圖1所示。改變墩高參數和分聯形式進行了E1反應譜分析。

模型中1#墩為最高墩，5#墩為最低墩，墩高依次遞減，具體墩高布置見表1。按照相鄰墩高差的不同，分為1-1、1-2、1-3三組，各組墩高差逐漸增大，由5 m增大到10 m再到20 m。與此同時，最大墩高也在一次增加。模型1-1整體墩高相對較矮，模型1-3整體墩高最高，模型1-2介于兩者之間。每組模型采用了兩種分聯形式：6跨一聯和2×3跨一聯。6跨一聯在橋臺處設置滑板支座，橋墩上設置等剛度板式支座。2×3跨一聯在3#墩上設置滑板支座，其余支座布置同6跨一聯。

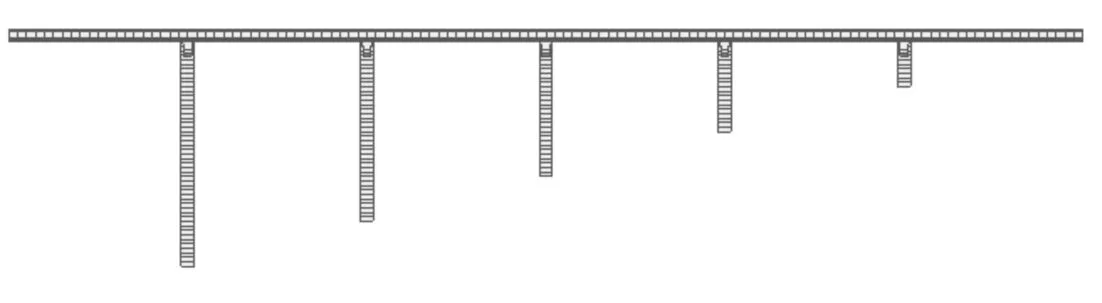
圖1 有限元模型

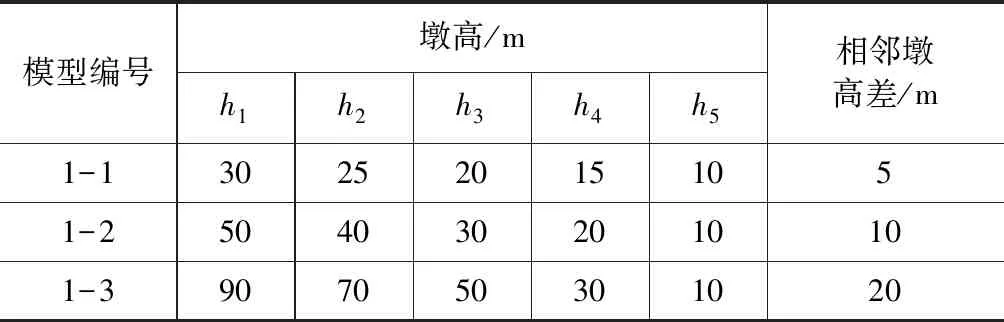
表1 各模型墩高參數

全橋為6孔40 m跨預應力連續T梁，每孔由5片T梁組成，T梁梁高2.5 m。橋墩為等截面獨柱矩形空心墩，橫橋向長4.5 m，縱橋向長3 m。T梁采用C50混凝土，墩身、蓋梁采用C40混凝土。橋臺處布置聚四氟乙烯滑板支座，各橋墩處布置5個板式橡膠支座，剪切剛度2 896 kN/m。橋梁抗震設防類別屬于B類，橋址處地震動峰值加速度0.20g，特征周期0.35 s，場地類型為II類。

2 長短聯動力特性對比

長短聯形式下，不同模型的前5階自振頻率見表2。模型1-1長聯形式下的的一階頻率為0.440 Hz，是短聯一階頻率(0.282 Hz)的1.56倍。在高階頻率上，長聯更是顯著大于短聯：長聯下模型1-1的第5階自振頻率是短聯的3.15倍。類似的模型1-2和模型1-3也均是長聯頻率大于短聯。模型1-2與模型1-3的長聯一階頻率分別是相應短聯形式的1.59倍和1.65倍。自振頻率大意味著橋梁結構周期短，剛度大，有利于改善山區橋梁自振頻率低、結構柔、變形大的問題。究其原因在于采用長聯形式時，左側高墩一聯與右側矮墩一聯相互串聯在一起，矮墩短聯在一定程度上彌補了高墩短聯剛度過小的缺點，因而基頻較短聯形式有所增加。值得說明的是，從模型1-1到模型1-3，長聯與短聯一階頻率的倍數關系逐漸增大，從此可以看出，當墩高越大時，采用長聯對提升橋梁結構自振頻率的作用越明顯。

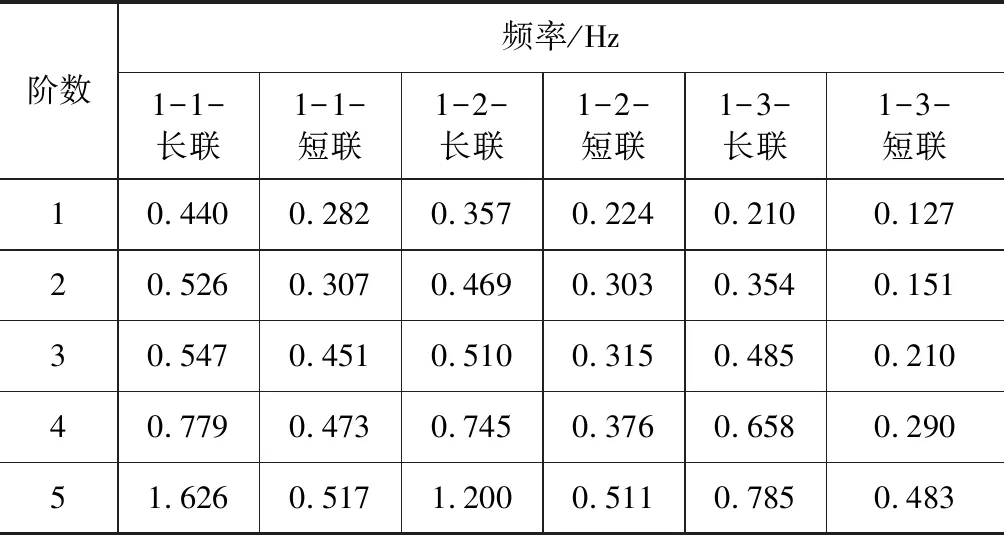
表2 不同模型前5階自振頻率

長聯和短聯首次出現的面外和面內振型見表3。長聯最先出現的面外振型為主梁橫向彎曲，而短聯則是主梁橫向平轉。這是因為短聯形式下，在3#中間墩上布置的是聚四氟乙烯滑板支座，無法對上部主梁結構形成有效約束。長聯下首次出現的面內振型是橋墩縱向彎曲，相比之下，短聯只在高墩一側發生縱向彎曲。由此不難看出，短聯橋梁較長聯橋梁整體性差，這是不利于橋梁結構抗震的。

3 墩底內力對比

在地震作用下，梁橋橋墩的內力最大位置在墩底處，因而墩底截面受力為最不利。本小節主要對比了長短聯形式下墩底的剪力和彎矩。

各組模型在不同的分聯形式下的墩底剪力如圖2～圖4所示。在兩種分聯形式下，橋墩墩底縱橋向剪力總體都表現為矮墩大，高墩小，即矮墩承受了較大的剪力，是高墩縱橋向剪力值的1～2倍。與短聯橋梁相比，長聯橋梁在1#和2#高墩上，長聯墩底縱向剪力更小。與此相反的是，在4#和5#矮墩上，長聯墩底縱向剪力較大。在3#墩處，長短聯墩底縱橋向剪力相差不多。造成上述現象的原因是長聯橋梁將左側高墩部分與右側矮墩部分連接起來后，矮墩區因其剛度大，上部結構質量引起的剪力更多地向矮墩集中。

墩底橫向剪力在各墩之間分布規律不是很明顯。采用長聯時，墩底橫向剪力基本符合“矮墩大，高墩小”這一規律。但在采用短聯時，最大墩底橫向剪力值出現的位置不定。多數橋墩在采用短聯時橫向剪力更大，但在最矮的5#墩處恰恰相反，長聯下其墩底橫向剪力更大，在模型1-2中，長聯比短聯橫向剪力大了24 %。

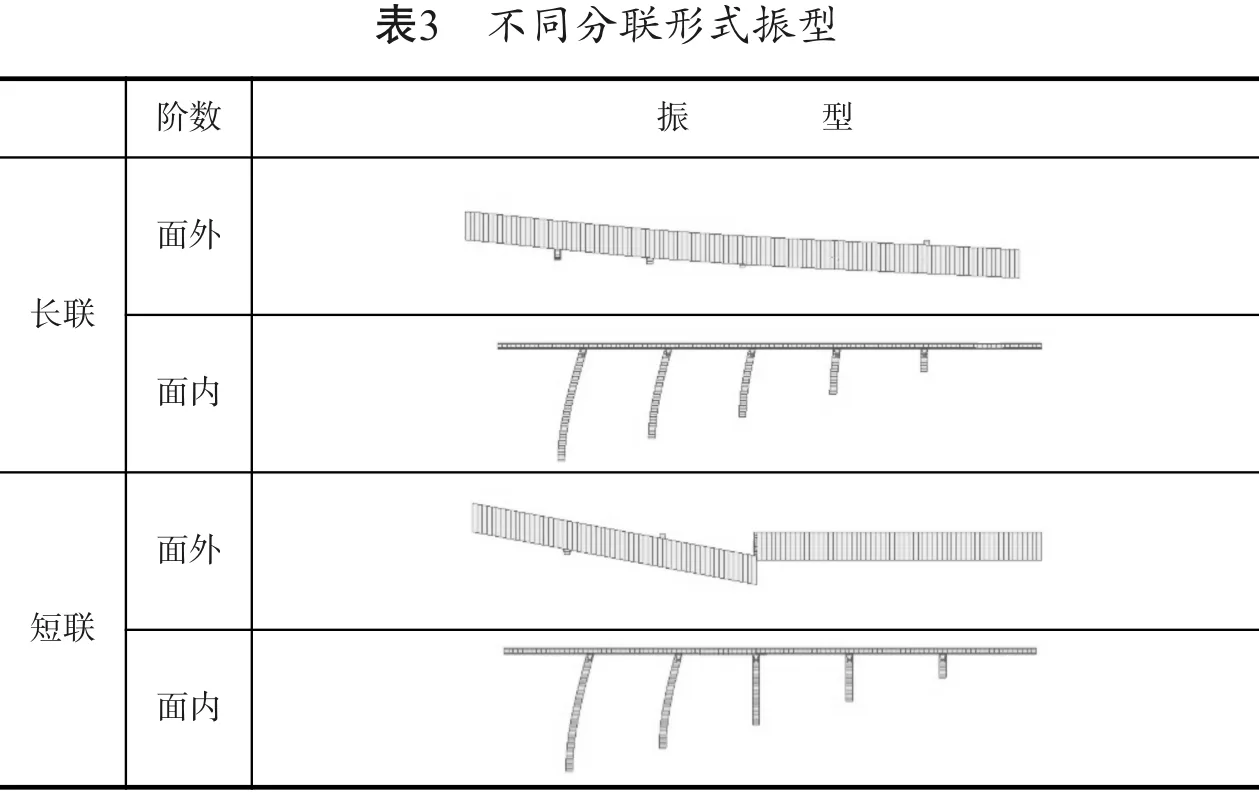
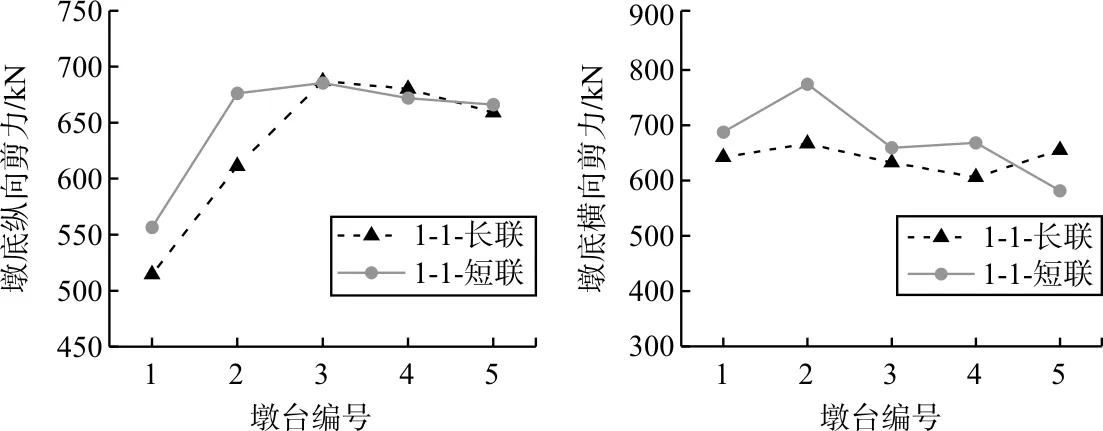
圖2 地震作用下模型1-1墩底縱橫向剪力

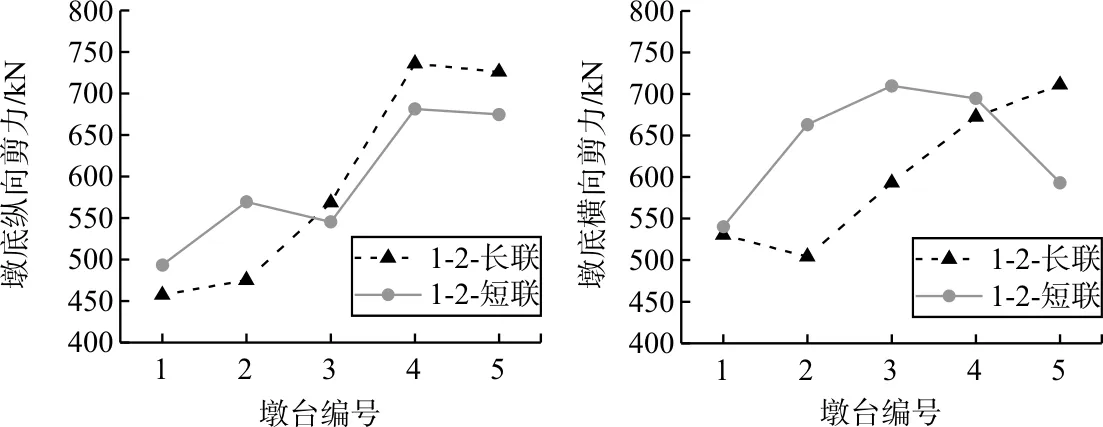
圖3 地震作用下模型1-2墩底縱橫向剪力

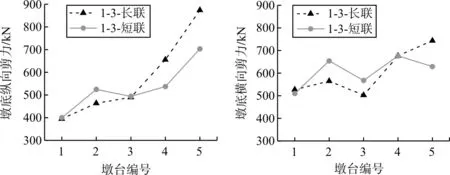
圖4 地震作用下模型1-3墩底縱橫向剪力

不同模型在不同分聯形式下的墩底彎矩如圖5～圖7所示。從圖5可以看出，模型1-1作為I類橋梁中整體墩高最矮的一組，在兩種分聯形式下，墩底縱橋向彎矩相差不多。在1#和2#兩個相對較高墩處，長聯形式的墩底縱橋向彎矩比短聯形式減小了約2 000 kN·m，相對減少了12 %。模型1-2和模型1-3的高墩墩底縱向彎矩分別減少了23 %和35 %。值得注意的是，模型1-3的4#墩底縱向彎矩較短聯增加了27 %，這是因為上部結構傳遞到4#墩的剪力較大，即使其不是最高墩，力臂不是最長，最終墩底縱向彎矩反而最大。

一般情況下，長聯橋梁的墩底橫向彎矩要小于短聯橋梁，特別是在2#墩處，短聯下其墩底橫向彎矩最大值均出現在2#墩處，其彎矩值是長聯的1.5倍。長聯形式下5#墩和1#墩底橫向彎矩有可能略大于短聯，但相差不大。同時對比墩底縱向彎矩，采用短聯時，墩底縱向、橫向彎矩最大值均出現在2#墩處。相比于1#墩，2#雖然較矮，只看橋墩時，地震作用下彎矩小于高墩，但2#墩相對剛度大，分配的水平力更大，綜合起來反而墩底彎矩更大。5#墩因其墩身最矮，高度只有10 m，所以其自身質量小，再加上水平力臂短，導致地震作用下彎矩最小。整體上看，相對于長聯，采用短聯時，墩底橫向彎矩分布更加不均。

圖5 地震作用下模型1-1墩底縱橫向彎矩

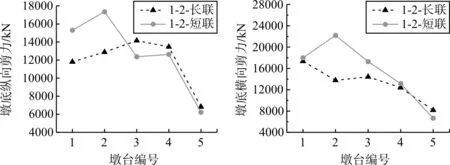
圖6 地震作用下模型1-2墩底縱橫向剪力

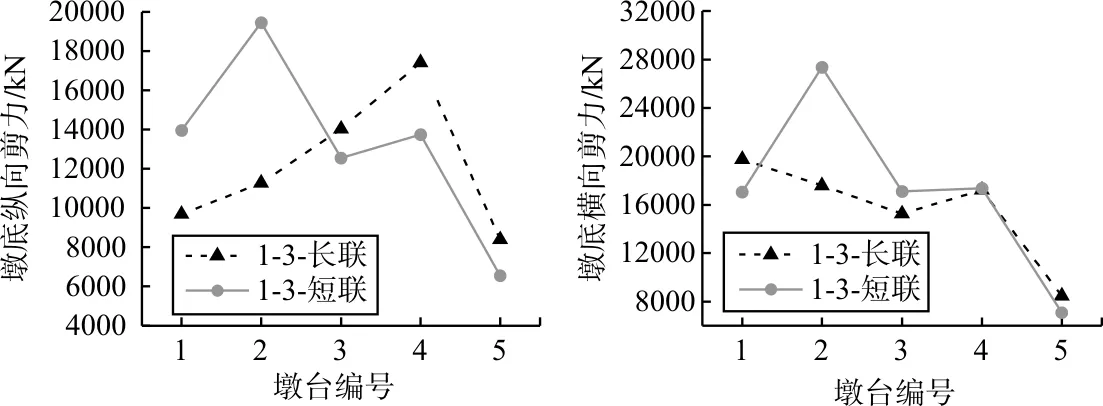
圖7 地震作用下模型1-3墩底縱橫向剪力

4 結論

為了提高山區橋梁的抗震性能，本文分析對比了長聯和短聯兩種分聯形式對橋梁地震響應的影響，主要有以下幾點結論。

(1)長聯形式下橋梁結構的基頻要大于短聯形式，在高階頻率上這一現象更加明顯。

(2)采用長聯形式，會使橋梁結構整體性更好，有利于各墩之間協同抗震，比短聯形式更具優勢。

(3)地震作用下，長聯橋梁的縱向和橫向剪力表現為矮墩大，高墩小。短聯橋梁的縱向剪力分布也符合上述規律，但橫向剪力分布規律不明顯。

(4)長聯形式下的墩底最大縱向和橫向彎矩要小于短聯形式，且相比于短聯，墩底彎矩分布更為均勻。

綜上所述，針對山區橋梁所具有的兩點特征，采用長聯形式能提高橋梁結構的抗震性能，減小地震響應，相比采用短聯更加有利。