基于BMST編碼的超Nyquist傳輸系統性能研究

譚　雪，李雙洋，白寶明，余忠洋

(1.西安電子科技大學 綜合業務網理論及關鍵技術國家重點實驗室，西安 710071；2.通信網信息傳輸與分發技術重點實驗室，河北石家莊 050081)

0　引言

在1975年，貝爾實驗室的Mazo首次提出了超奈奎斯特(Fast-than-Nyquist，FTN)傳輸的概念[1-2]，為人們提供了一種新的提高頻譜效率的方法。FTN是一種非正交傳輸技術，它突破了傳統的無記憶傳輸技術，通過人為添加可控的符號間串擾(Intersymbol Interfere，ISI)[3-4]來實現頻譜效率的提高。而且Mazo還證明了當時間加速因子τ大于一定值時，FTN傳輸系統的誤碼特性漸近收斂于傳統傳輸系統的誤碼特性。顯然，FTN傳輸技術有著很好的應用前景。但在實際應用中也存在著很多弊端，比如，為了消除FTN傳輸系統中固有的ISI，其接收機會面臨巨大的譯碼復雜度[5]。2013年，Yong Jin、Daniel Kim 和Jan Bajcsy提出了一種基于非等功率分配的二元分層FTN傳輸方案[6]。該傳輸系統可以實現低復雜度的FTN譯碼，同時還可以在較大的信噪比下接近頻譜效率極限。

5G 通信是面向2020 年以后的移動通信需求而發展的新一代移動通信技術[7-8]。根據移動通信的發展規律，5G 通信將具有很高的頻譜利用率和能效，在傳輸速率和資源利用率等方面較4G 移動通信提高了一個量級[9]。而FTN傳輸技術就是一種能夠有效提高頻譜效率的非正交傳輸技術。因此，將FTN傳輸技術應用到5G通信中具有非常重要的意義。對于分層FTN傳輸系統，通過調節每一層的碼率或功率進行多級譯碼，從而實現干擾抵消的目的。作為一種碼率靈活可調的編碼方法——分組馬爾科夫疊加傳輸編碼[10-11]，與分層FTN傳輸系統的結合有著相當重要的意義。

在2013年，馬嘯等人在多用戶系統中的分組馬爾科夫疊加編碼的基礎上提出了分組馬爾科夫疊加傳輸(BMST)[12-13]。通過耦合生成矩陣的方式，構造出一種較為靈活的類似空間耦合碼的長卷積碼[14-15]。通過仿真發現：在較高的信噪比和足夠的碼長下，BMST編碼的性能是可預測的，且當使用重復碼或者單奇偶校驗碼作為基本碼時，其誤碼性能(10-5數量級下)與香農極限僅差0.5 dB[16]。

在FTN和BMST的基礎上，本文將碼率靈活可變的BMST編碼和分層FTN傳輸結合起來而構造出一種新的傳輸系統，并通過仿真驗證了該系統可以顯著提高其頻譜效率。

1　分層FTN傳輸系統模型

1.1　分層FTN信號

假設當前FTN傳輸系統的速率是Nyquist傳輸系統的K倍，即整個FTN傳輸系統分為K層，則發送信號可以表示為：

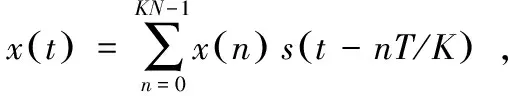
(1)

式中，T為Nyquist傳輸間隔，N為每層的符號數，x(n)為第n個所需傳輸的符號，s(t)為脈沖成型函數。為了便于分析，上式可以進一步分解成：

(2)

且xk(n)=x(Kn+k-1)，k=1,2,...,K，n=0,1,…,N-1。

1.2　分層FTN信號的發送

基于BMST編碼的分層FTN傳輸系統發送端結構圖如圖1所示。將滿足統計獨立同分布的KN×1二元信息序列u=[u(0),u(1),…,u(KN-1)]T劃分成K個獨立的N×1子向量u1,u2,…,uK，即：

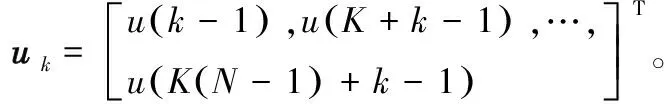
(3)

接著，對這K個子向量進行BMST編碼。 然后，根據非等功率分配的原則，將得到的K個編碼后的比特流c1,c2,…,cK映射到星座點上，即對所有的n，有x1(n)∈{±P1T},x2(n)∈{±P2T},...,xK(n)∈{±PKT}。不失一般性，假設功率分配滿足PK≥PK-1≥…≥P1，對應的調制符號向量為：

x=[x(0),x(1),…,x(KN-1)]T。

(4)

最后，經過FTN調制器生成FTN信號，發送到信道中。

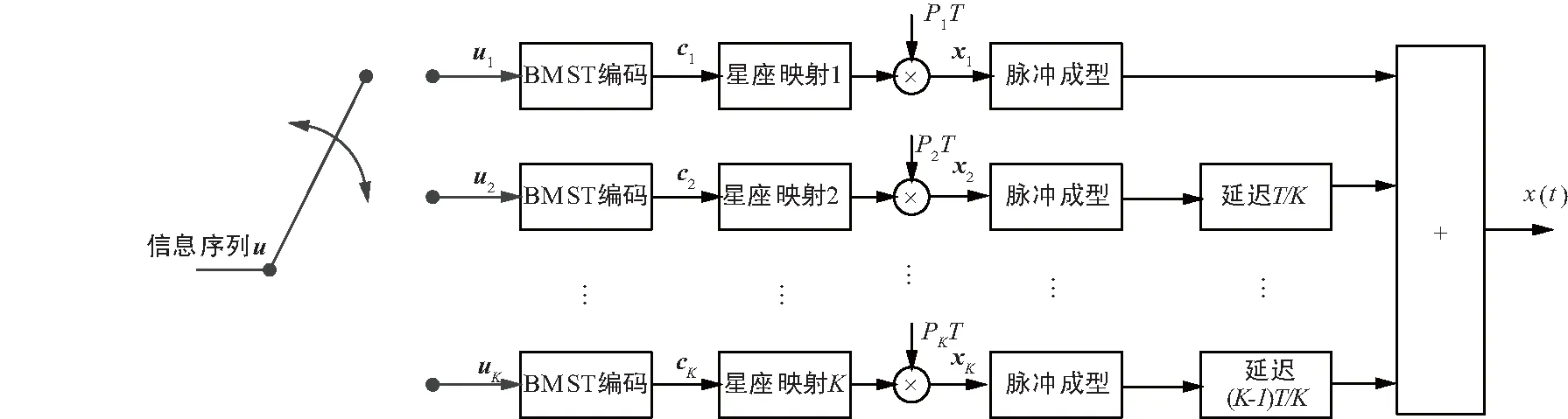
圖1　基于BMST編碼的分層FTN傳輸系統發送端結構

1.3　分層FTN信號的接收

圖2給出了基于BMST編碼的分層FTN傳輸系統接收端結構。該結構是基于多級譯碼的，即，將已經進行過BMST譯碼的層當作加性噪聲處理。假設在加性高斯白噪聲(Addictive White Gaussian Noise，AWGN)信道下，每層采用二進制相移鍵控(Binary Phase Shift Keying，BPSK)調制。

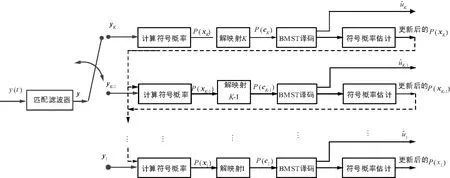
圖2　基于BMST編碼的分層FTN傳輸系統接收端結構

接收信號y(t)=x(t)+z(t)，其中z(t)為白噪聲。假設采用相干檢測，經過匹配濾波器，并以FTN速率K/T進行采樣，得到的離散時間匹配濾波器采樣結果y，可以寫為：

y=Hx+z。

(5)

H為KN×KN的Toeplitz矩陣，表示碼間干擾，其第i行第j列個元素寫為hi-j，由于FTN傳輸帶來的碼間串擾(ISI)：

(6)

式中，z為KN×1維的色噪聲向量，協方差矩陣為(N0/2)H。將y分成K個子向量y1,y2,…,yK，即：

yk=[y(k-1),y(K+k-1),…,y(K(N-1)+k-1)]T,
k=1,2,…,K,

(7)

式中，yk的第n個元素滿足yk(n)=y(Kn+k-1)。根據y=Hx+z和xk(n)=x(Kn+k-1)，yk(n)可以寫成xk(n)的函數，即：

(8)

式中，z(Kn+k-1)為第k層的第n個噪聲采樣。由z的協方差矩陣可知，相同層的n個噪聲采樣之間相互獨立同分布。為了簡化上式，考慮任意T正交的單位能量的脈沖成型函數s(t)，即：

(9)

式中，δ(m)為沖激函數。基于以上分析，式(8)可簡化為：

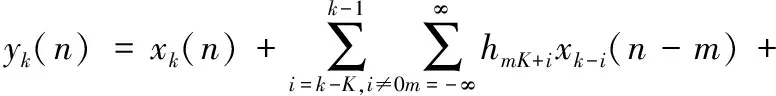
(10)

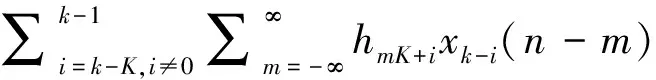
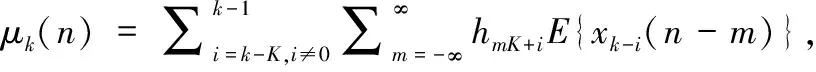
(11)

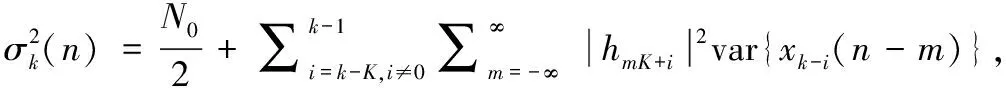
(12)

式中，E{·}表示期望運算，var{·}表示方差運算。

根據中心極限定理，隨著接收符號長度的增加，式(10)中的ISI項可以近似看作高斯隨機變量。因此，可以利用高斯概率密度函數來近似計算當前xk(n)的后驗概率，即：

(13)

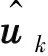
最后，經過上述一次整體譯碼之后，再利用更新后的P(xK),P(xK-1),...,P(x1)做下一次的整體譯碼。同時這些更新后的概率還可以用來優化ISI加噪聲項的均值和方差，從而得到更好的后驗概率近似。

2　BMST編譯碼原理

2.1　編碼算法

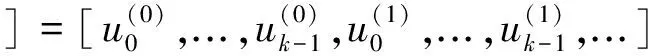
編碼過程初始化，當t<0時，u(t)=〇；當t≥0時，對應的碼字通過下式得到：

c(t)=u(t)G0+u(t-1)G1+…+u(t-m)Gm，

(14)

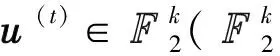
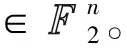
循環：t=0,1,…,L-1時，

② 對1≤i≤m，使用第i個交織器Πi對v(t-i)進行交織，記為w(i)；

③ 計算c(t)=v(t)+∑1≤i≤mw(i)，作為待傳輸的第t個分組。

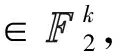
2.2　譯碼算法

圖3給出了一個分組數L=4和約束長度m=2的BMST譯碼系統結構圖。圖中有4種類型的節點，每一條邊代表一個隨機變量序列。

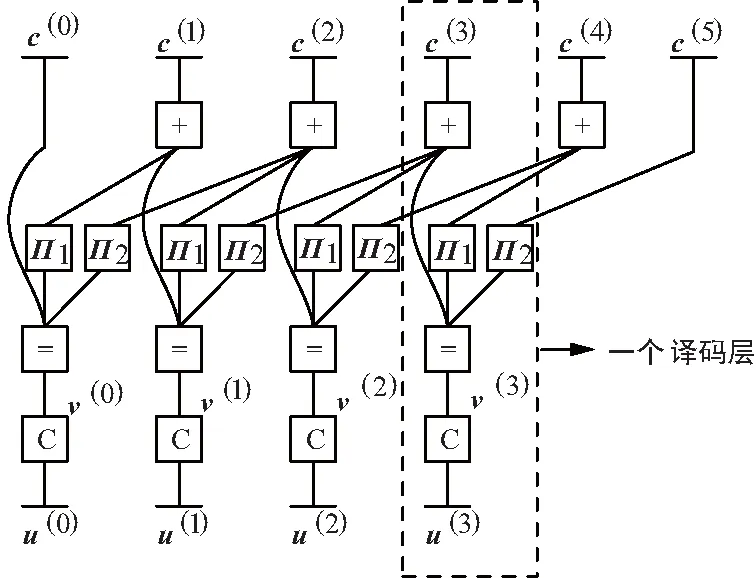
圖3　L=4,m=2的BMST系統一般因子圖

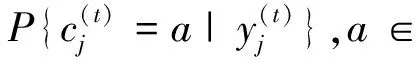
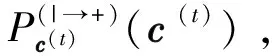
滑窗譯碼：對于t=0,1,...,L-1和I=1,2,...,Imax。

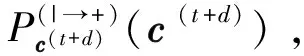
② 迭代：對于I=1,2,...,Imax。

a.前向遞歸：i=0,…,min(d,L+m-1-t)，第t+d層的信息傳遞過程如下：

b.后向遞歸:i=min(d,L+m-1-t),…,0，第t+d層的信息傳遞過程如下：

式中，a∈2，j=0,1,…,n-1，i=1,2,…,m。

3　系統性能仿真

3.1　分層FTN層數K對系統性能的影響

首先通過仿真分析分層FTN層數即加速因子K對系統性能的影響。仿真參數：AWGN 信道，BPSK 調制。基本碼參數：4狀態的(2,1,2)卷積碼，生成矩陣G(D)=[1,(1+D+D2)/(1+D2)]，信息序列長度k=50，碼長n=104，碼率Rc≈0.5。BMST結構參數：分組數L=19，約束長度m=1，總碼率R=0.456 7，最大迭代次數Imax=18。分層FTN傳輸參數：滾降因子β=0.22，信號間隔T=1，時間截斷長度為15T，加速因子K=1、2、3。圖4給出了不同層數下，基于BMST編碼的分層FTN傳輸系統的誤比特性能曲線。

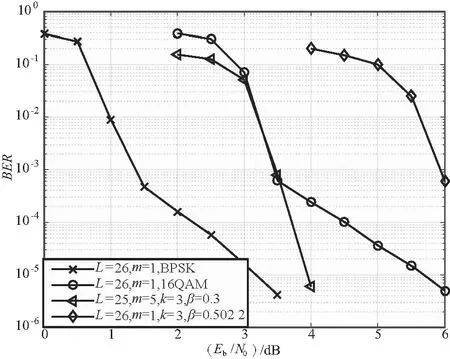
圖4　系統仿真結果曲線

根據FTN傳輸系統頻譜效率的計算公式(即η=R·N·K/(1+β))，可以計算出圖4中3條曲線(分別對應K=1、2、3)的二維頻譜效率η1=0.748 7、η2=1.497 4和η3=2.246 1，對應的無差錯傳輸所需的信噪比分別大約為4 dB、6.5 dB和10 dB。顯然，通過超Nyquist速率傳輸的方法可以提高系統的頻譜效率，而帶來了性能的下降。

3.2　相同譜效率下的性能比較

為了凸顯FTN可以提高通信系統頻譜效率的特點，通過調整BMST的參數L和m來保證系統的頻譜效率不變的情況下，分析對比系統的性能。

通過仿真對比Nyquist情況下，采用16QAM調制、K=3的FTN傳輸和BPSK調制下的系統性能。根據FTN通信系統中頻譜效率的計算公式：

η=R·N·K/(1+β) 。

(15)

當使用BMST編碼時，上式可以寫成：

(16)

式中，k為基本碼信息位長度，n為基本碼碼長，L和m為BMST結構參數。

選擇BMST參數使其滿足在Nyquist情況下，采用16QAM調制和K=3的FTN傳輸，BPSK調制時系統的頻譜效率相同，具體的參數選擇如下：

① Nyquist情況，16QAM，m=1，L=26，R=0.478 8，η1=1.912 4；

② FTN傳輸，K=3，BPSK，m=5，L=25，R=0.414 4，β=0.3，η2=1.912 4；

③ FTN傳輸，K=3，BPSK，m=1，L=26，R=0.478 8，β=0.502 2，η2≈1.912 4。

①～③有相同的頻譜效率，②中改變了BMST結構的參數，帶來了0.064 4的碼率損失，③中沒有碼率損失，增加了β值并使頻譜效率和①中相同。對列出的3種情況進行仿真，所有仿真均在AWGN信道下，卷積碼參數采用4狀態的(2,1,2)卷積碼，生成矩陣G(D)=[1,(1+D+D2)/(1+D2)]，信息序列長度k=358，碼長n=720，碼率Rc=0.497 2，BMST最大迭代次數Imax=8。FTN信號間隔T=1，時間截斷長度為15T。

圖5　相同譜效率下的性能比較

圖中從左邊開始的第2條線是采用BPSK調制，3層FTN的傳輸結構，第3條線是傳統Nyquist情況下的16QAM調制，可看出，在相同的頻譜效率下，通過BMST編碼和FTN結合的傳輸方式可以得到更好的系統性能。對比第4條線，可以看出，BMST編碼可以在較小的碼率損失下獲得較大的額外編碼增益。也就是說，FTN可以有效提高通信系統的頻譜效率。

4　結束語

將BMST編碼與FTN傳輸相結合，構造出了一種碼率靈活，性能可預測易分析，可以有效提高頻譜效率的通信系統。使用了一種基于非等功率分配的分層FTN結構，將ISI當作高斯噪聲處理，該方法有效降低了由ISI導致的譯碼復雜度。在AWGN信道下進行仿真，證明該系統可以有效提高頻譜效率。在相同的頻譜效率下，與傳統Nyquist情況下的高階調制做對比，通過FTN傳輸獲得了更好的性能。

[1]Mazo J E.Faster-than-Nyquist signaling [J].Bell System Technical Journal,1975,54(8): 1451-1462.

[2]Rusek F,Anderson J B.Constrained Capacities for faster-than- Nyquist Signaling[J].IEEE Trans.Inf.Theory,2009,55(2): 764-775.

[3]Rusek F,Anderson J B.Multistream faster-than-Nyquist Signaling[J].IEEE Transactions on Communications,2009,57: 1329-1340.

[4]Liveris A D,Georghiades C N.Exploiting faster-than-Nyquist Signaling[J].IEEE Transactions on Communications,2003,51:1502-1511.

[5]Colavolpe G,Foggi T,Modenini A,et al.Faster-than-Nyquist and beyond: how to Improve Spectral Efficiency by Accepting Interference[J].Optics Express,2011,19:26600-26609.

[6]Yong J,Daniel K,Jan B.Binary Faster than Nyquist Optical Transmis Sion via Non-uniform Power Allocation [C]∥in Proc.Canadian Workshop Inf.Theory,Toronto,ON,2013: 180-185.

[7]ITU-R.Report ITU-R M.2370 - IMT Traffic estimates for the years 2020 to 2030[R].Geneva:ITU-R,2015.

[8]IMT-2020 (5G) 推進組.5G 愿景與需求白皮書[R].北京: IMT-2020 (5G) 推進組,2014.

[9]ITU-R.Recommendation ITU-R M.2083 - Framework and Overall Objectives of the Future Development of IMT for 2020 and Beyond[R].Geneva : ITU-R,2015.

[10] Ma X,Liang C,Huang K,et al.Block Markov Superposition Transmission: Construction of Big Convolutional Codes from Short Codes [J].IEEE Trans.Inf.Theory,2015,61(6): 3150-3163.

[11] Liang C,Hu J,Ma X,et al.A New Class of Multiple-rate Codes Based on Block Markov Superposition Transmission[J].IEEE Trans.Signal Process.,2015,63(16):4236-4244.

[12] Ma X,Liang C,Huang K,et al.Obtaining Extra Coding Gain for Short Codes by Block Markov Superposition Transmission[C]∥ in Proc.IEEE Int.Symp.Inf.Theory,2013:2054-2058.

[13] Huang K,Mitchell D G M,Wei L,et al.Performance Comparison of LDPC Block and Spatially Coupled Codes Over GF (q)[J].IEEE Trans.Commun.,2015,63(3):592-604.

[14] Liang C,Ma X,Zhuang Q,et al.Spatial Coupling of Generator Matrices: A General Approach to Design Good Codes at a Target BER [J].IEEE Trans.Commun.,2014,62(12): 4211-4219.

[15] Liang Chulong,Ma Xiao,Bai Baoming.Spatial Coupling of RUN Codes via Block Markov Superposition Transmission [C]∥in Proc.High Mobility Wireless Communications (HMWC 2015),2015: 6-10.

[16] Hu Jingnan,Ma Xiao,Liang Chulong.Block Markov Superposition Transmission of Repetition and Single-Parity-Check Codes [J].IEEE Trans.Commun.,2015,19(2):131-134.