基于無量綱性能指標的渠系控制器參數優化

管光華，鐘 錁，廖文俊，肖昌誠，蘇海旺

?

基于無量綱性能指標的渠系控制器參數優化

管光華，鐘 錁，廖文俊，肖昌誠，蘇海旺

（武漢大學水資源與水電工程科學國家重點實驗室，武漢 430072）

為研究性能指標對渠系控制器參數優化的效果，該文基于無量綱性能指標，利用MATLAB程序“渠系控制仿真系統”整定了PI控制器參數，同時進行了仿真對比分析。在梳理渠系控制指標領域現有研究成果的基礎上，文章首先以渠池固有參數對現有渠系性能指標進行無量綱化處理及追加，并進一步衡量各水位、流量、時間指標的相關性和代表性建立了含權重的綜合指標。在程序“渠系控制仿真系統”平臺上，采用實例驗證法結合2個設計流量約為170 m3/s、8 m3/s的不同規模渠系進行了分析驗證。結果表明：無量綱性能指標能夠比較不同渠系的控制優劣，并可確定其優化目標數量級；以綜合指標在E-3數量級為控制器優化目標，可同時滿足各單一無量綱性能指標的優化要求，較好地均衡系統逐項動態性能；流量指標和閘門開度指標存在高耦合關系，在2個實例中其相關度分別為0.995、0.993；控制器比例系數—流量指標變化曲線存在敏感與否的分區，時間積分常數對水位指標敏感，作用曲線呈“U”型。研究提出的無量綱性能指標及綜合指標可比較不同規模渠系控制系統性能，也適用于渠系的控制器參數優化設計，對中國大量的調水工程渠道運行調度及灌區渠網調控具有一定的參考價值。

渠道；自動化；優化；動態性能指標；PI控制器參數優化；數值仿真；無量綱化

0 引 言

明渠輸水系統的控制主要有2種方式：傳統的人工控制和現代的自動化控制方式。人工控制已經逐步為自動化控制的運行方式所取代。渠道自動化即為提高渠系運行的傳統方法所實施的控制系統[1]。自動化控制方式分為水位控制[2-3]、流量控制、蓄量控制[4]；當地控制與中央集中控制[2,5]等，常用的渠道系統控制模型有ID[2-3,6]、IDZ[7-8]、IR[9]，渠系運行方式也可根據控制點位置分為下游常水位、上游常水位、等體積和控制體積法[10]。渠池響應特性研究[9,11-12]、模型預測控制[13-16]、神經網絡[17-19]及多控制理論結合[20]等方法也逐漸應用到輸水系統中以改良渠池控制性能。自動化控制在國內外明渠輸水系統取得了較為廣泛的應用。如美國中亞利桑那工程（CAP）采用等體積運行方式以穩定性、響應迅速性、經濟性為目標，已成功運行三十多年[21]；澳大利亞Haughton Main Channel（HMC）采用系統辨識模型建立了渠道自動化控制模型，可以較準確地預測渠池中水位變化[22-23]；國內的南水北調[24]、引黃濟青、引黃入晉等也部分實行了渠系自動化[25]。

渠系控制首要難點在于確定性能指標，并參照該指標進行控制器參數優化求解。目前在渠道控制性能指標領域相關研究較少。ASCE渠道控制算法工作組（ASCE Task Committee on Canal Automation Algorithms）于1998年提出了一系列基本控制性能指標[26]，對渠系控制性能進行優劣衡量。然而其指標系統采用的水位、流量指標等皆為有量綱指標，其數值僅具有相對意義難以用于衡量不同的控制系統與控制算法。Strelkoff等[27]通過對經典的非恒定流控制方程進行無量綱處理時，發現無量綱形式的圣維南方程與經典圣維南方程有相似的表達形式，去量綱后的控制方程可忽略渠道規模的影響。本文試圖參照這一思路對現有性能指標進行去量綱處理。

本文擬建一套無量綱化性能指標集，可適用于不同渠系、不同工況下控制器控制效果的量化衡量，也可用于新建渠道系統的控制器優化設計。本文對現有的渠系控制性能指標以渠池固有參數為依據做無量綱化處理以及指標追加，并進一步提出了基于水位偏差、流量變化、穩定時間建立的含權重的綜合指標。利用MATLAB程序“渠系控制仿真系統”的平臺，選取國內一大型調水工程的輸水渠道和ASCE位于加利福尼亞的小型測試渠道為代表性實例進行應用，依次以各無量綱單一性能指標及綜合指標為優化準則整定仿真系統中PI控制器參數，同時對比了各優化準則下控制器參數的控制效果。此外，討論無量綱性能指標受控制器參數影響的規律，提出了控制器參數優化設計的基本原則，并使其具有一定魯棒性。

1 渠系控制系統性能指標及評價

1.1 無量綱單一性能指標集

渠道控制系統的大滯后性、強非線性、高耦合特性及多輸入多輸出的拓撲結構，決定了渠道系統動態性能指標的多樣性和復雜性。ASCE渠道控制算法工作組[26]提出了含有量綱的指標體系，包括7項指標：最大絕對誤差（maximum absolute error，MAE）、穩態誤差（steady- state error，StE）、絕對值誤差積分（integral of absolute magnitude of error，IAE）、絕對流量變化積分（integrated absolute discharge change，IAQ）、絕對閘門開度積分（integrated absolute gate movement，IAW）、水位誤差平方積分（integrated square of error，ISE）、流量誤差平方積分（integrated square of discharge change，ISQ）。但在具體應用到不同渠系控制器的設計時無法比較控制性能，在設計渠道控制系統前也無法確定指標的優化目標。

在其研究基礎上，出于實際渠道工況的迥異以及統一設定控制標準的需要，建立一套無量綱指標集：MAE、StE、IAE本身不帶量綱，保留其原有形式；ISE、IAQ、IAW、ISQ分別基于渠池的控制點目標水位、設計流量、最大閘門開度等固有參數進行無量綱化處理改進為無量綱化水位誤差平方積分（nondimensionalintegrated square of error，NISE）、無量綱化絕對流量變化積分（nondimensional integrated absolute discharge change，NIAQ）、無量綱化 絕對閘門開度積分（nondimensionalintegrated absolute gate movement，NIAW）、無量綱化流量誤差平方積分（nondimensionalintegrated square of discharge change，NISQ），弱化因渠池規模造成的控制系統性能指標的差異，并建議對ISQ略去其存在的懲罰系數R，因該數值需針對不同的渠道進行率定，為非先驗性參數，可操作性不強。其次，考慮實際運行需求，追加部分指標：

（1）

式中為渠池長度，m；v為重力波傳播速度，m/s。

2）最大水位降速（maximum drawdown velocity of water level，MDV）：本文參照有關工程目前對于水位降落的約束，限定系統每24 h水位降落值不超過0.3 m；每小時水位降落值不超過0.15 m。

初步建立了渠系控制各無量綱單一性能指標集，如表1所示。

表1 渠系控制各無量綱單一性能指標集初建

注：為時間，s；1、2分別為流量變化開始時刻和穩定時刻；D為控制系統離散時間步長，s；為系統仿真總時間，s；y為時刻測量水位，m；y為控制點目標水位，m；Q為時刻過閘流量，m3/s；Q1、Q2分別為1、2時刻過閘流量，m3/s；Q為渠池設計流量，m3/s；W為時刻閘門開度，m；1、2分別為1、2時刻閘門開度，m；W為閘門最大開度，m；T為系統的穩定時間，s；D為以重力波為基礎的延遲時間，s。

Note:is time, s;1,2are the moment for flow changing and stabilizing;Dis discrete time step of control systems, s;is simulation time, s; yis the measured water level at timem; yis the aimed water level of the control pointm;Qis the flow rate at timem3/s;Q1,Q2are the flow rate at time1,2respectively,m3/s; Qis the design discharge, m3/s; Wis the gate opening at timem;1,2are the gate opening at time1,2respectivelym;Wis the full-gate opening, m;Tis the time that it takes for regaining stability, s;Dis the delay time based on gravity waves, s.

總體看來，無量綱單一性能指標集分別權衡了渠系水位、流量、閘門、時間、水位降速各因素的影響，削弱了因渠池固有參數帶來的指標值的差異。但在實際應用中還存在一些問題：第一，指標數量較多，且應用于不同衡量因素的指標數量并不均衡；第二，人為割裂了各指標間的關聯和約束，以各單個性能指標為優化準則進行控制器參數優化時，難免導致其優化卻同時帶來另一部分指標劣化的效果。

1.2 綜合指標的選擇與建立

以單一指標為控制器的優化準則時，操作困難，控制效果難以全面均衡。故本文試圖探討不追求單一指標的最優性而平衡系統整體性能的控制方法，犧牲單個指標的最優而保證更多指標得到同時滿足的策略。

對各無量綱單一性能指標進行分析：首先確定系統需要進行的衡量因素：水位、流量、時間是系統評定的基本要素。而水位降速的衡量MDV這個指標可簡化為渠系控制中的開關判定，凡超過允許值系統立即報警，該組控制器無效，而控制器尋優只在有效控制中尋找。此外，由成因關系分析，本次仿真計算引用了美國中亞利桑那調水工程（CAP）的過閘流量計算公式，見式（2），這是一種由自由出流向淹沒出流過渡的流量系數計算方法[28]，閘門開度直接控制渠道過流；并采用卡爾·皮爾遜的積差法相關系數進行NIAW與NIAQ的相關性分析，其公式如式（3）。可知，閘門動作的衡量指標NIAW與流量的衡量指標NIAQ存在耦合關系，且流量指標不受死區等限制比閘門指標更為敏感，故以流量指標來間接衡量閘門因素。

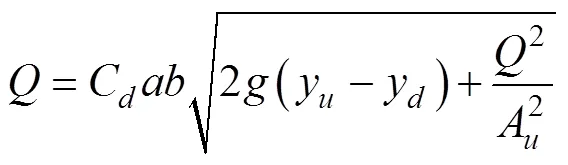
式中為過閘流量，m3/s；C為流量系數；為閘門開度，m；為閘門寬度，m；y、y為閘門上、下游水深，m；A為閘門上游過水斷面面積，m2。

式中為相關性系數，為，2個系列的平均值，σ、σ為變量、變量及變量的標準差，σ為協方差。

故在綜合指標中不選取衡量水位降速、閘門因素的性能指標。

其次，確定衡量水位、流量、時間因素較適宜的性能指標。MAE是水位波動極值，不能反映系統水位波動的平均情況；StE與最后一次調節動作密切相關，具有較大的偶然性。IAE衡量過渡過程中的水位波動情況，而NISE又與IAE相似，故選取IAE衡量仿真過程中水位整體變化的情況。同樣地，NIAQ衡量過渡過程中的流量波動情況，NISQ與NIAQ相似。而NIAQ又與閘門指標具有耦合關系，故采用NIAQ反映渠池中流量變化狀況。渠道響應穩定比尺作為時間指標，直接反映控制效果的快速性。

式中為經驗系數，根據管理對渠系響應速度的要求選取不同的權重，本文對流量、水位、穩定時間三者要求較均衡故選取=1，取值越大則系統對穩定時間的要求越高，同時也會帶來較大的超調量和水位、流量波動，實際選用時需根據設計者對控制性能的要求進行調整。

2 程序“渠系控制仿真系統”

基于MATLAB語言設計的“渠系控制仿真系統”[29]，可實現在渠系控制器的不同優化準則下渠池內水位、流量、閘門開度變化過程的仿真。在輸入渠系物理參數建立渠系模型后，控制仿真系統通過渠系水力計算將系統狀態譬如水位、流量等信息傳遞給給控制器，控制器將這一系統狀態與目標狀態進行比較，根據預設的控制邏輯，輸出給流量開度轉化模塊并執行閘門開度變化。其模型結構如圖1所示，各個模塊緊密聯系、相互作用，以實現渠池按所設計的運行方式運行。在該渠系控制仿真系統中，“前饋+反饋控制器”最為關鍵。

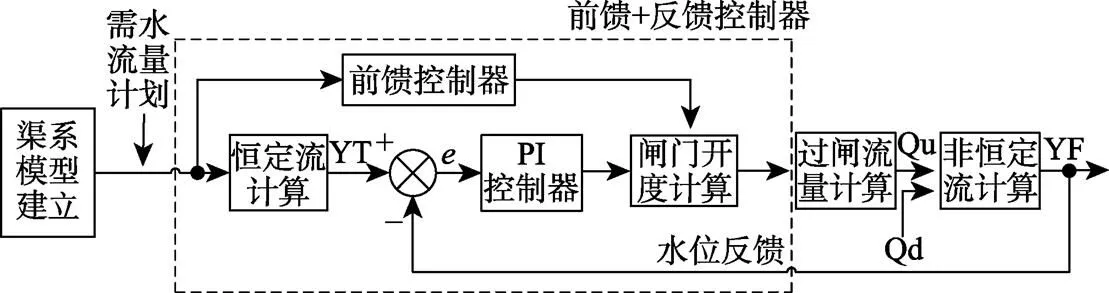
注：YT為控制目標水位，m；YF為模擬預測得到的水位，m；e為水位偏差，m；Qu、Qd分別為渠池上游流量和下游流量，m3×s-1。

控制器的控制方式采用前饋與反饋相結合的控制方式。前饋控制控制流量，反饋控制控制水位，分別設計出流量前饋控制器和水位反饋控制器來共同調節閘門開度，控制器輸出為經疊加后的閘門開度變化值。并須同時滿足閘門死區及最大閘門開啟速度的限制條件，才能作為閘門啟閉設備的最終輸入值。流量控制器使用流量而非水位作為輸入量，采用流量控制器作為前饋控制，其基本思想為通過控制蓄量法得出每個閘門的預分配流量，同時通過圣維南方程組計算出渠道上一時刻的閘前后水位，再根據過閘流量公式反推閘門開度。PI反饋控制器根據對比預測水位與目標水位間偏差及偏差變化率，根據控制器參數輸出反饋流量，達到消除誤差、整定系統的目的，見式（5）。在該“前饋+反饋控制器中”，需要整定的參數為PI反饋控制器的比例系數（）、時間積分常數（）。

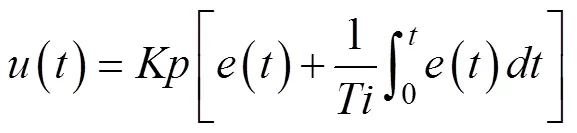
式中()為反饋控制器輸出流量，m3/s；為比例系數；為積分時間常數；Δ為控制系統離散時間步長，s；()為時刻的水位偏差，m。

3 測試及結果分析

選擇2個具有代表性的規模差異顯著的渠系，分別利用渠系仿真控制系統進行控制模擬，2個渠系規模差別在20倍以上。

渠系1為通過類比國內某工程得到的大型渠道，全長24 km，底坡0.000 04，糙率0.015，邊坡為2，設計流量170 m3/s。渠系2為ASCE渠道控制算法工作組位于加利福尼亞的小型渠道[26]，全長18 km，底坡0.000 1，糙率0.02，邊坡為1.5，設計流量沿程隨渠底寬度的減小由8 m3/s減小到6 m3/s。渠系示意圖見圖2，采用下游常水位控制方式，閘門充分過流。本文對小流量取水工況（取水流量為初始下游流量的20%左右）進行探討。2個渠系取水口均設定為在第1、3號渠池下游段進行線性取水，渠池流量可表示如式（6）。渠系1初始下游流量35 m3/s，2 h內2個取水口各取5 m3/s；渠系2初始下游流量1.4 m3/s，10 min內各取水口各取0.2 m3/s。

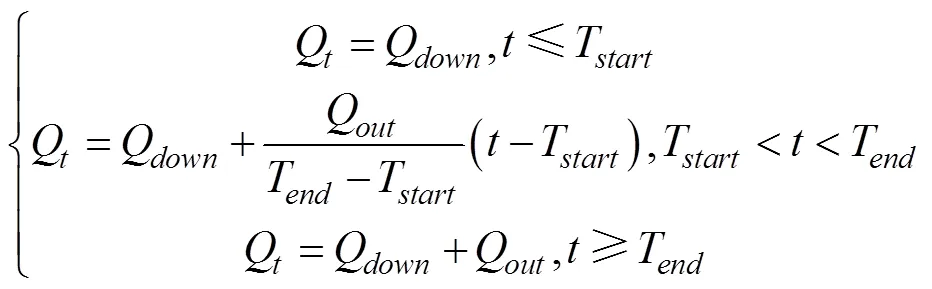
式中為時間，s；Q、Q分別為初始下游流量、計劃取水流量，m3/s；T、T為計劃取水開始及結束時間，s；Q為任意時刻流量，m3/s。

3.1 無量綱單一指標優化結果

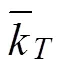
注：長度單位：m

表2 各單個指標準則下的控制器參數及相應指標值

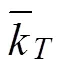
由上述可以看出，以不同的指標為控制器的優化準則時結果差異顯著，采用單一指標進行系統優化結果往往不理想。如仿真結果算例2-2（圖3b）以StE為單一目標指標進行優化時，追求極小的穩態誤差必然帶來閘門的反復調節，造成了水位的震蕩和控制時間的延長。單指標優化人為地割裂了各指標間的關聯和約束，難免導致部分指標優化而同時帶來另一部分指標劣化的效果。實際渠系控制中，受到實際管理和監測水平的制約，追求單一指標的最優難以取得滿意結果。故參照綜合指標進行尋優是必須的。控制系統的平穩性、精確性與快速性兼顧，是渠系控制的正確方式。

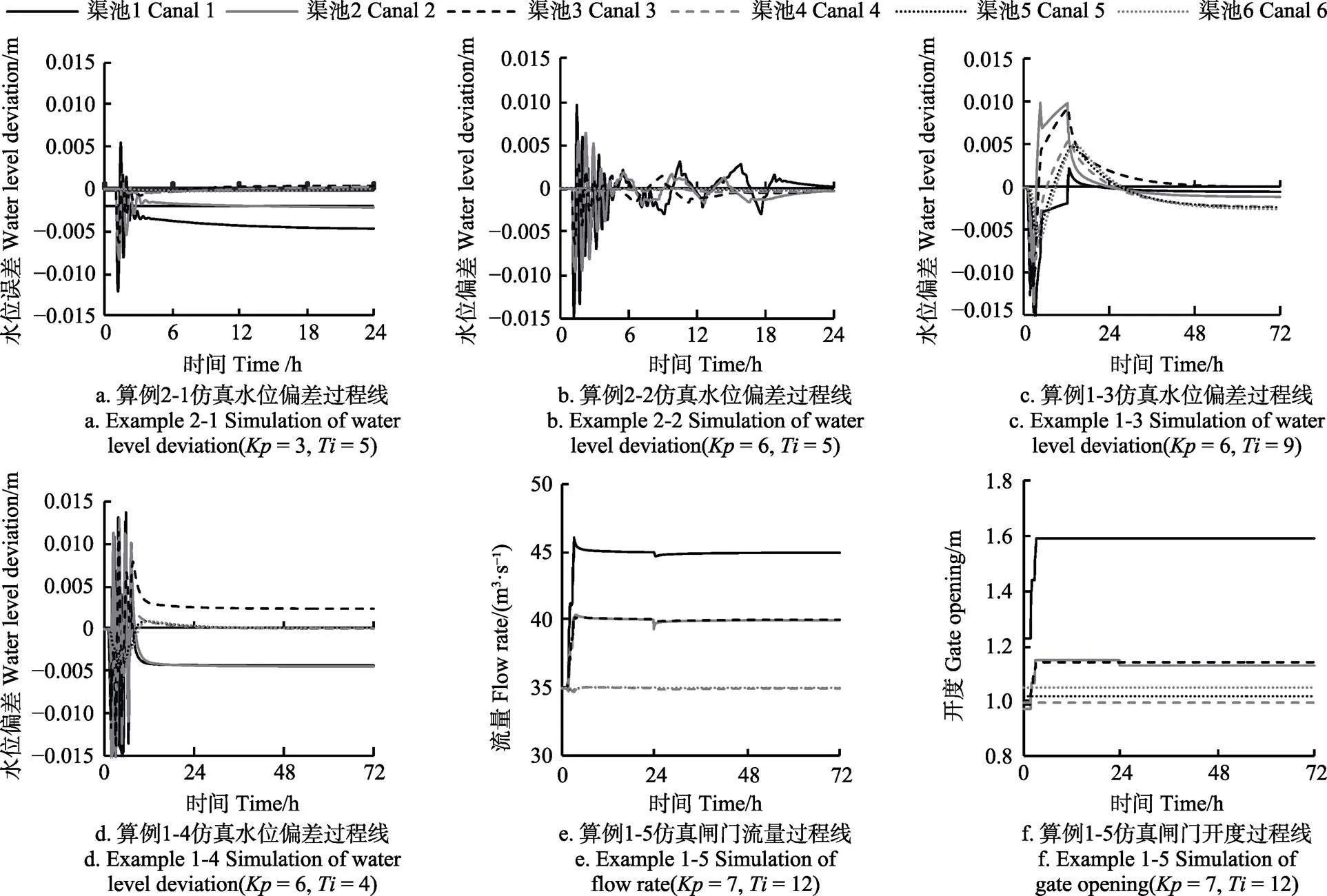
注：命名算例X-Y規則，X為渠系編號，Y為對應指標最優的編號（Y值1～5依次代表MAE及，STE，IAE，NISE，NIAQ、NIAW及NISQ最優）。

3.2 綜合指標優化結果與評價

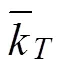
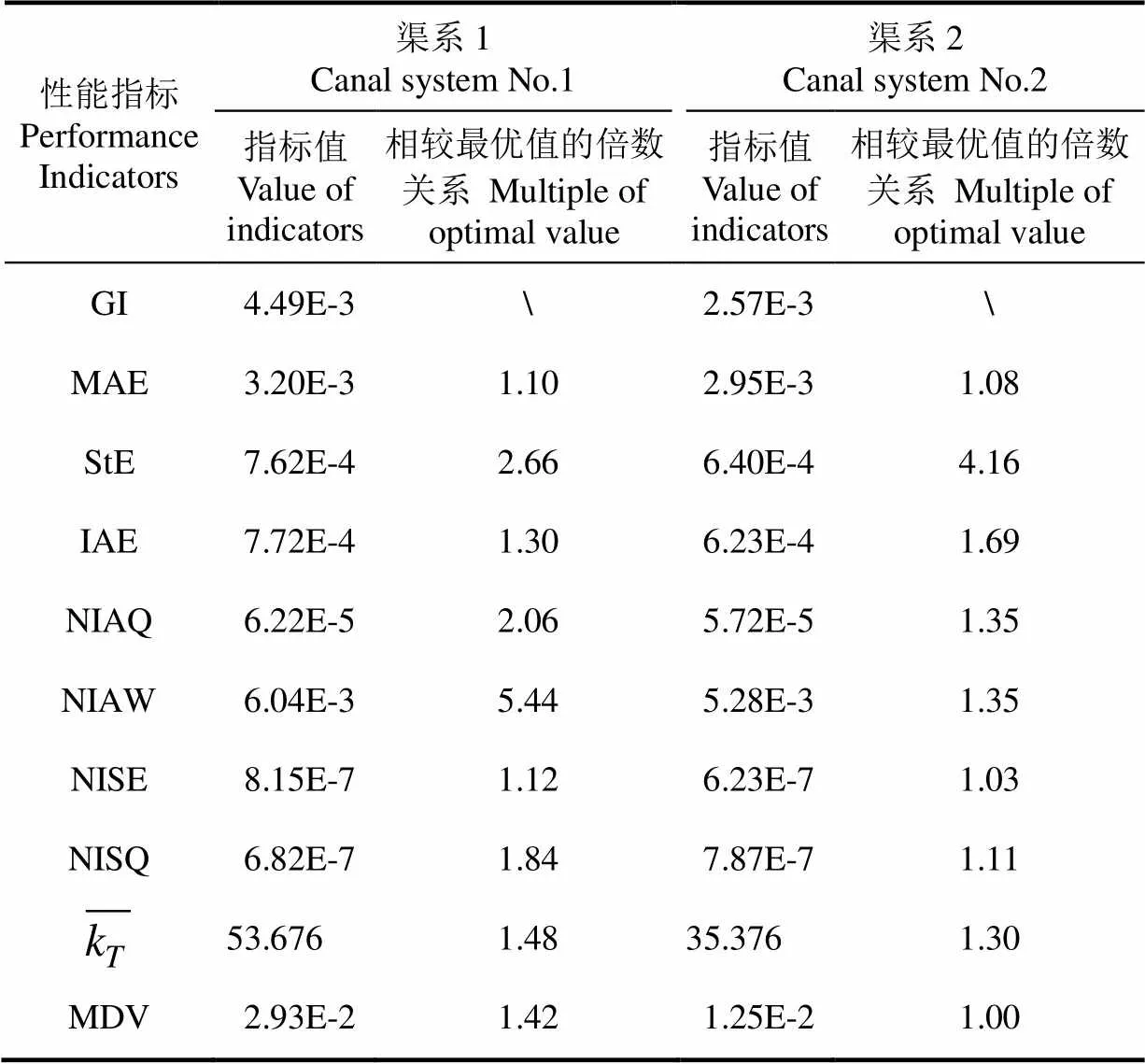
表3 GI優選控制器性能指標

據綜合指標GI優選出的控制器參數控制效果與單一指標相比，效果較好，如圖4。算例1-6與前述算例相比有了進一步優化，閘門動作小，在4 h內即可實現閘門不再動作；最大水位誤差雖從0.015 m增加到0.02 m，但很好地控制在允許范圍內，且其水位波動能夠很快穩定。算例2-6兼顧水位收斂速度及穩態誤差，在6 h左右經過閘門的最后一次動作使實際水位極其接近目標水位值。

3.3 NIAQ與NIAW的相關性分析

在指標集中，NIAQ與NIAW具有較高的相關性。在一般工況下，閘門的開度變化會直接引起渠池內過閘流量的變動，且二者成正相關關系。但同時死區的存在以及渠池中水位的波動，過閘流量的波動通常較閘門開度的波動劇烈且持續時間長。經過相關系數分析，其積差法相關系數可達到0.8以上，呈高度相關。故在綜合指標衡量因素的選擇中，以流量指標NIAQ來間接反映閘門性能的優劣是合理的。

注：命名X-Y規則與圖3相同，X為渠系編號，Y為對應指標最優的編號（6為GI最優）

表4 NIAQ、NIAW相關度

實際上，本次仿真計算中渠道為緩坡明槽恒定流向非恒定流過渡過程。假定非恒定流為一元流動，過水斷面上流速均勻分布，斷面上水面水平過水斷面的動水壓強分布符合靜水壓強分布規律，其為單一的渠系水流最理想情況[30]。而現實受水力學因素及渠床變形因素的影響，明槽中水位、流量關系呈繩套曲線或更復雜的曲線，所以閘門開度與流量關系在不同的流態之間亦存在繩套曲線甚至躍變的情況，從而導致NIAQ與NIAW真實情況下的相關度具有一定不確定性。

3.4 無量綱指標變化規律探討

在控制器設計中，借助控制器參數、對無量綱指標的影響來探尋控制器參數與指標間的關系，從而為控制器設計提供捷徑。二者在成因上有相關關系，控制器參數決定了控制效果，控制效果量化后即為性能指標。本文采用控制變量法探討無量綱指標在控制器參數作用下的變化規律，交替固定比例參數（）和積分時間常數（）的方法，繪制控制器參數與性能指標的關系曲線。

在該影響分析過程中，為控制器參數、限定一定范圍及選取合適的距離步長。本文2個渠系由控制仿真系統整定出：的適宜計算范圍在1～9，距離步長為1；為0.5～200，因積分作用減弱過程的非線性故距離步長隨積分作用的削弱而增大，從1變化為10。

控制器的比例環節（）控制響應迅速，但往往存在一定超調，使得流量誤差呈增大趨勢，在非敏感區（渠系1為<15，渠系2為<4，如圖5a）NIAQ增長速度緩慢，在敏感區域呈指數增長形式。不同渠池由于渠道蓄量的差異導致渠池對響應的敏感區間存在較大差異，渠系1總蓄量較大，對流量變化具有較大的調節能力，在較大的范圍內變動都可以維持NIAQ指標在優良指標E-5數量級。在渠系控制中，相鄰節制閘間的渠池存儲有效的蓄量對減小流量波動是有利的。

靜帶區的設置對水位性能指標有較大的影響。當閘門動作及水位測量精度很高時，只通過調節就能獲得較好的控制效果，但受實際操作限制往往還需要積分環節。渠系2中閘門死區、水位死區設置為毫米級，精度極高，積分調節作用被削弱；渠系1死區設置為厘米級，工程實際運用較多，故針對渠系1中積分調節的作用進行分析。

積分時間常數對水位指標敏感。相較比例調節，引入積分作用一般能夠有效優化水位誤差指標（MAE、StE、IAE）。取值較大，積分作用被削弱，主要以調節為主；但取值過小時，過調節易使水位變動劇烈，部分參數下控制不良，指標值呈尖銳波峰狀突增（如圖5b），主要原因是積分作用明顯的情況下穩定誤差與最后一次調節量有關，而其相對具有一定的隨機性本文認為能夠客觀反映系統水位控制性能的指標為IAE，其值較大有2種可能，一是過渡過程震蕩嚴重，二是穩態誤差較大，這二種情況皆為控制器設計中應避免的。對IAE及MAE的作用曲線也類似于圖5b，大體呈偏“U”型曲線。盆底部位低平，存在小幅的波動，局部參數控制性能很好地穩定在優化數量級里，正是控制目標所追求的。且隨著的增加參數對于控制性能指標的敏感度減弱，較大的才會造成性能指標的突增。

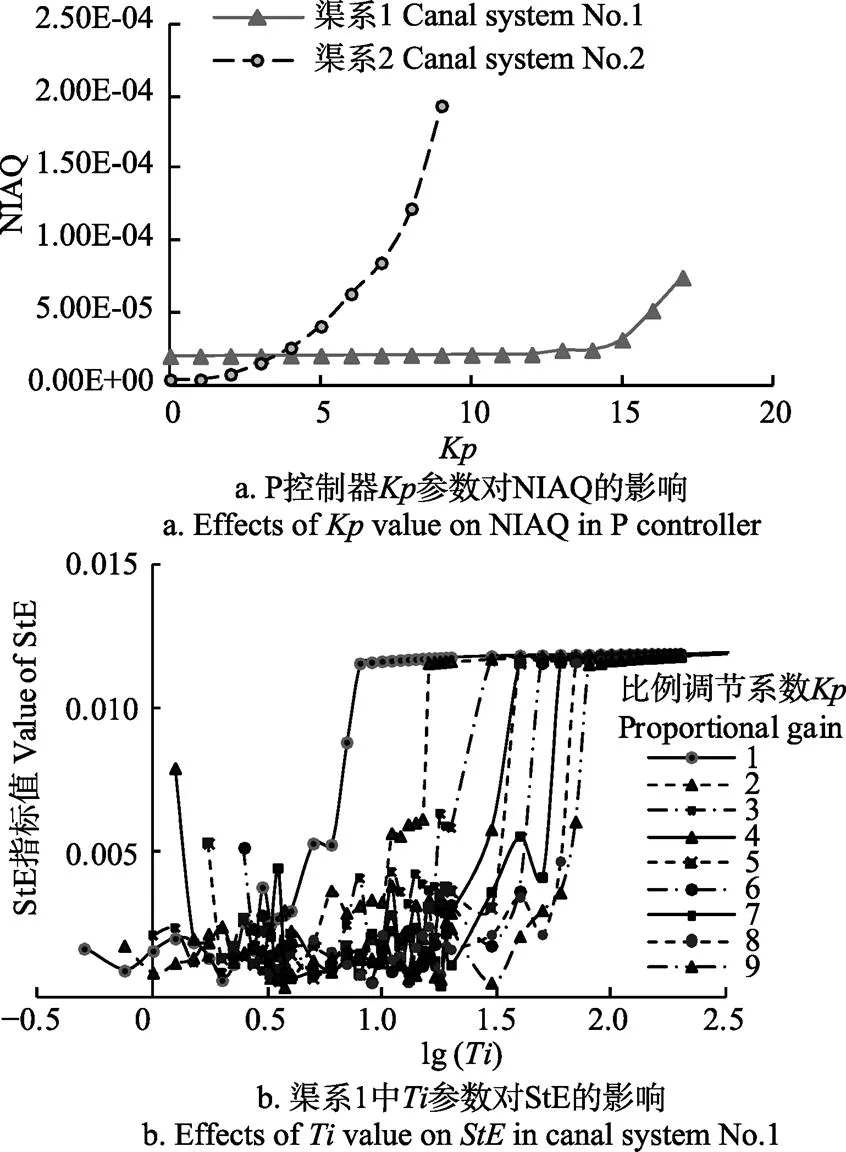
圖5 控制器參數對指標的影響

此外，在實際工程控制中由于系統自身的不確定性以及仿真模型與物理模型之間的差異，要求控制器必須具有一定的魯棒性[31]。如圖5所示，一般情況下，渠系的控制參數在一定范圍內，均可使性能指標值在優化目標數量級內，即可稱其為控制優良。控制優良的控制器參數范圍越廣，表示該渠系在該種取水工況下調節適應能力越好。可以推測，在不同取水工況下，在其控制優良的控制器參數范圍的交集中選取一組控制參數，該組控制參數魯棒性能好，能適應一定范圍內的隨機取水工況，正是在實際工程中所希望采用的控制器。

基于以上分析，提出了控制器參數設計的基本原則：

1）當前已經提出了不少可適用于實際工程的工程整定法，方法較為簡單，原理清晰。如Zieler-Nichols整定公式法[32]，根據系統的階躍曲線獲得比例系數、慣性常數、純延遲時間常數并建立經驗公式轉化為、；ATV工程整定法，Litrico等[33]由系統具有的增益裕量和相角裕量建立了PID控制器中、的計算公式。

2）工程整定法整定出的控制器參數一般適用于簡單規整渠道，在實際運用中，對渠道斷面變化較大、建筑物較多的復雜渠道往往控制效果不佳，且在渠道運行初期沒有積累該工程控制參數的整定經驗，故需要用試算法進行仿真整定。本文認為在閘門、水位死區不構成對控制精度的極大限制的條件下，控制器參數可按以下規律進行整定：

①、對系統的調節作用有顯著差異，對系統敏感性也不盡相同。比例控制對水位偏差做快速響應，直接影響了系統從一個穩態到另一個穩態的過渡時間，較小時不易造成超調，緩慢接近目標，加大可以提高系統響應速度，但太大容易導致系統震蕩甚至失穩。此外，比例控制獨立作用下，系統水位的穩態誤差無法消除。積分控制對水位偏差在時間上的積分做響應，在流量初步達到穩定后控制水位偏差收斂的速度，消除偏差直至死區內，但積分作用太強會造成系統的過分敏感而引發水位震蕩。總體說來，比例作用較為強烈，但積分作用比較敏感，容易造成系統的失穩。在圖6中，定性比較了不同、組合對無量綱單一性能指標的作用效果，雷達圖上各點值偏離中心越遠表示其性能越不佳。

②一般說來，的作用效果會強于，故在參數整定中先進行比例控制的整定。將積分時間設為無窮大，參照工程整定法初步計算出的比例參數，在其附近區域內進行尋優。若系統響應慢、呈現過阻尼特性，則應加大；若水位過程超調較大、往復震蕩、呈現欠阻尼特性，則應減小。初步整定得到后，再進行的整定。整定從一個大值緩慢減小，且因變化的非線性尋優距離步長需逐步減小。整定得到后，再重新縮小的尋優步長進行整定，如此反復2～3次，基本可以得到一組比較符合控制要求的控制參數。

③多渠段進行聯合整定時，可結合渠池的響應特性曲線。延遲時間較長的渠段選擇較大參數以加快控制效果，水面面積較小的渠段適當減小積分作用防止出現水位震蕩。

圖6 不同Kp、Ti組合對單個無量綱化控制指標的定性作用

4 結 論

本文構建了無量綱單一性能指標集和綜合指標，以2個規模超過20倍的渠道工程為代表在渠系控制仿真系統中加以應用，驗證無量綱單一性能指標集和綜合指標的可行性，本文得出以下結論：

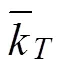
2）本文設計了渠系控制仿真系統的PI控制器，以各無量綱單一性能指標與綜合指標為優化準則對代表性渠系進行控制器參數整定，并對比分析。仿真分析確定了各無量綱單一指標的優化目標數量級：最大絕對誤差（MAE）為E-3、穩態誤差（StE）E-4、絕對值誤差積分（IAE）E-4、無量綱化絕對流量變化積分（NIAQ）E-5、無量綱化絕對閘門開度積分（NIAW）E-3、無量綱化水位誤差平方積分（NISE）E-7、無量綱化流量誤差平方積分（NISQ）E-7、渠道響應時間比尺E1。但追求單個無量綱性能指標的優化難免偏頗，難以全面滿足系統控制要求。而以綜合指標在E-3數量級為控制器參數優化準則全面衡量了水位、流量、時間3因素性能，各無量綱單一性能指標也可以滿足各自優化數量級的優化要求，水位、流量波動平緩，渠道系統較快達到穩定。

3）PI控制器參數共同協調控制系統，性能指標與控制器關系的探求有助于快速選取符合要求的參數。該文探求了無量綱性能指標隨控制器參數的變化規律。NIAQ隨著參數變化呈現不同區域內的敏感性差異，當渠系1中>15、渠系2中>4時，NIAQ由緩慢增長的非敏感區變為指數增長的敏感區，且各區域大小受渠池蓄量的影響；參數對水位指標敏感，作用效果呈現“U”型曲線，存在一段適宜的區間使水位指標較好地穩定在優化數量級內。并基于控制器參數與控制性能的影響分析提出了控制器優化設計的基本原則：以工程整定法進行初步整定；再根據強調節與強敏感性的特點以試算法進行與多次輪換整定。

此外，無量綱性能指標中二次型性能指標NISE、NISQ，于二次型最優控制（Linear quadratic regulator，LQR）中系數矩陣和建立的應用值得進行嘗試探討。

渠道控制的目標是系統過渡過程的平穩、快速、準確，以達到適時、適量供水的目的。采用性能指標來比較不同渠系性能的優劣，也可將其作為準則來優化控制器參數。仿真模型與物理模型的差異使得一味追求單一指標最優化顯得毫無意義，控制在一定的優化范圍即可基本滿足控制要求，在實際系統中將這一定量優化范圍作為系統滾動優化的基礎也是一種較好的思路。由于控制器參數自身具有較強的魯棒性，優化的目標只是讓控制器參數落在一定的最優域內。結合適當的系統魯棒性分析可以保證優化結果可行，作為系統運行期間自適應調整的基礎。

[1] 美國內務部墾務局著. 現代灌區自動化管理技術實用手冊[M]. 高占義，謝崇寶，程先軍，譯. 北京：中國水利水電出版社，2004.

[2] Wahlin B T, Clemmens A J. Automatic downstream water-level feedback control of branching canal networks: theory[J]. Journal of Irrigation and Drainage Engineering, 2006, 132(3): 198－207.

[3] Wahlin B T, Clemmens A J. Automatic downstream water-level feedback control of branching canal networks: simulation results[J]. Journal of Irrigation and Drainage Engineering, 2006, 132(3): 208－219.

[4] 姚雄，王長德，李長菁. 基于控制蓄量的渠系運行控制方式[J]. 水利學報，2008，39(6)：733－738. Yao Xiong, Wang Changde, Li Changjing. Operation mode of serial canal system based on water volume control method[J], Journal of Hydraulic Engineering, 2008, 39(6): 733－738. (in Chinese with English abstract)

[5] Malaterre P O, Rogers D C, Schuurmans J. Classification of canal control algorithms[J]. Journal of Irrigation and Drainage Engineering, 1998, 124(1): 3－10.

[6] Guan G, Clemmens A J, Kacerek T F, et al. Applying water-level difference control to Central Arizona Project[J]. Journal of Irrigation and Drainage Engineering, 2011, 137(12): 747－753.

[7] Litrico X, Fromion V. Simplified modeling of irrigation canals for controller design[J]. Journal of Irrigation and Drainage Engineering, 2004, 130(5): 373－383.

[8] Clemmens A J, Tian X, van Overloop P J, et al. Integrator delay zero model for design of upstream water-level controllers[J]. Journal of Irrigation and Drainage Engineering, 2017, 143(3): B4015001.

[9] van Overloop P J, Miltenburg I J, Bombois X, et al. Identification of resonance waves in open water channels[J]. Control Engineering Practice, 2010, 18(8): 863－872.

[10] 吳保生，尚毅梓，崔興華，等. 渠道自動化控制系統及其運行設計[J]. 水科學進展，2008，19(5)：746－755. Wu Baosheng, Shang Yizi, Cui Xinghua, et al. Automatic canal control system and its operation and design[J]. Advance in Water Science, 2008, 19(5): 746－755. (in Chinese with English abstract)

[11] Belaud G, Litrico X, Clemmens A J. Response time of a canal pool for scheduled water delivery[J]. Journal of Irrigation and Drainage Engineering, 2013, 139(4): 300－308.

[12] 李抗彬，沈冰，李智錄，等. 基于非恒定水流模擬的灌區明渠水力響應特征分析[J]. 農業工程學報，2015，31(10)：107－114. Li Kangbin, Shen Bing, Li Zhilu, et al. Open channel hydraulic response characteristics in irrigation area based on unsteady flow simulation analysis[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(10): 107－114. (in Chinese with English abstract)

[13] Aydin B E, van Overloop P J, Rutten M, et al. Offset-free model predictive control of an open water channel based on moving horizon estimation[J]. Journal of Irrigation and Drainage Engineering, 2017, 143(3): B4016005.

[14] Horváth K, Galvis E, Valentín M G, et al. New offset-free method for model predictive control of open channels[J]. Control Engineering Practice, 2015, 41(Supp. C): 13－25.

[15] van Overloop P J, Horváth K, Aydin B E. Model predictive control based on an integrator resonance model applied to an open water channel[J]. Control Engineering Practice, 2014, 27(Supp. C): 54－60.

[16] Tian X, Aydin B E, Negenborn R R, et al. Model predictive control for water level control in the case of spills[J]. Journal of Irrigation and Drainage Engineering, 2017, 143(3): B4016006.

[17] 韓延成，高學平. 基于RBF人工神經網絡的下游常水位自適應渠道輸水控制研究[J]. 西北農林科技大學學報(自然科學版)，2007，35(8)：202－206. Han Yancheng, Gao Xueping. Research of self-adapting canal downstream constant level control based on RBF neural network[J]. Journal of Northwest A&F University (Natural Science Edition), 2007, 35(8): 202－206. (in Chinese with English abstract)

[18] 韓延成，高學平，涂向陽，等. 基于CMAC神經網絡的自適應渠道輸水自動控制研究[J]. 灌溉排水學報，2007，26(2)：76－79. Han Yancheng, Gao Xueping,Tu Xiangyang, et al. Self- adapting canal automation control method based on CMAC neural network[J]. Journal of Irrigation and Drainage, 2007, 26(2): 76－79. (in Chinese with English abstract)

[19] 阮新建，姜兆雄，楊芳. 渠道運行神經網絡控制[J]. 農業工程學報，2006，22(1)：114－118. Ruan Xinjian, Jiang Zhaoxiong, Yang Fang. Neural control of channel operation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2006, 22(1): 114－118. (in Chinese with English abstract)

[20] 尚毅梓，吳保生，李鐵鍵，等. 閘前常水位輸水渠道的運行過程調控[J]. 清華大學學報(自然科學版)，2010，50(12)：1915－1919. Shang Yizi, Wu Baosheng, Li Tiejian, et al. Operational control for canal flow to maintain constant downstream depth[J]. Journal of Tsinghua University (Science and Technology), 2010, 50(12): 1915－1919. (in Chinese with English abstract)

[21] 范杰，王長德，管光華，等. 美國中亞利桑那調水工程自動化運行控制系統[J]. 人民長江，2006，37(2)：4－5.

[22] Eurén K, Weyer E. System identification of open water channels with undershot and overshot gates[J]. Control Engineering Practice, 2007, 15(7): 813－824.

[23] Ooi S K, Weyer E. Control design for an irrigation channel from physical data[J]. Control Engineering Practice, 2008, 16(9): 1132－1150.

[24] 黃會勇，劉子慧，范杰，等. 南水北調中線工程輸水調度初始控制策略研究[J]. 人民長江，2012，43(5)：13－18，63. Huang Huiyong, Liu Zihui, Fan Jie, et al. Study on initial control strategy of water conveyance dispatch of Middle Route Project of South-to-North Water Diversion[J]. Yangtze River, 2012, 43(5): 13－18, 63. (in Chinese with English abstract)

[25] 王念慎，郭軍，董興林. 明渠瞬變流最優等容量控制[J]. 水利學報，1989，(12)：12－20. Wang Nianshen, Guo Jun, Dong Xinglin. Optimal constant- volume control for transient flow in open channels[J]. Journal of Hydraulic Engineering, 1989, (12): 12－20. (in Chinese with English abstract)

[26] Clemmens A J, Kacerek T F, Grawitz B, et al. Test cases for canal control algorithms[J]. Journal of Irrigation and Drainage Engineering, 1998, 124(1): 23－30.

[27] Strelkoff T S, Clemmens A J. Nondimensional expression of unsteady canal flow[J]. Journal of Irrigation and Drainage Engineering, 1998, 124(1): 59－62.

[28] Clemmens A J, Strelkoff T S, Replogle J A. Calibration of submerged radial gates[J]. Journal of Hydraulic Engineering, 2003, 129(9): 680－687.

[29] 武漢大學. 輸水渠道系統運行仿真與控制軟件V1.0，2011SR034392，[CP/ DK]. 2011-06-03.

[30] 劉孟凱. 長距離輸水渠系冬季運行自動化控制研究[D]. 武漢：武漢大學，2012. Liu Mengkai, Operation Method of Long Distance Water Canal System in Winter[D]. Wuhan: Wuhan University, 2012. (in Chinese with English abstract)

[31] 管光華，王長德，范杰，等. 多渠段魯棒控制器的線性矩陣不等式解法[J]. 水利學報，2005，36(11)：1379－1384. Guan Guanghua, Wang Changde, Fan Jie, et al. Application of robust controler in automatic control of multi-section channel system[J]. Journal of Hydraulic Engineering, 2005, 36(11): 1379－1384. (in Chinese with English abstract)

[32] George Ellis著. 劉君華，湯曉君譯. 控制系統設計指南(第3版)[M]. 北京：電子工業出版社，2006.

[33] Litrico X, Malaterre P O, Baume J P, et al. Automatic tuning of PI controllers for an irrigation canal pool[J]. Journal of Irrigation and Drainage Engineering, 2007, 133(1): 27－37.

Optimization of controller parameters based on nondimensional performance indicators for canal systems

Guan Guanghua, Zhong Ke, Liao Wenjun, Xiao Changcheng, Su Haiwang

(430072,)

Automatic canal control plays an increasingly important role in water delivery systems, for it is effective in distributing the water resource rationally and reducing the discharge of wastewater. For the control of an open-canal system, the first issue is how to define the control performance indicator, and then the controller could be designed by pursuing the optimized value of performance indicators. The characteristics of canal systems result in the diversity and complexity of performance indicators, marked by big lag, strong nonlinearity, high coupling and multi-input multi-output (MIMO) topology. Therefore, the objective of this study was to improve the existing performance indicators and propose a general indicator reasonably and overall. We tried to demonstrate the feasibility of them by applying in 2 actual canal systems. In this paper, traditional performance indicators of canal control systems were concluded and analyzed, and some additional indicators were replenished and some of them are nondimensionalized by using the design discharge or constant depth of the control point or other inherent parameters. A set of indicators which can evaluate different canal systems were proposed by weakening the influence of canals’ dimension parameters. This set was applied to 2 canal systems with different scales: The large-size canal system is 24 km long × 15 m wide × 6 m deep and the small-size canal system is 18 km long × 5-7 m wide × 2.5 m deep, and the larger is around 20 times the size of the smaller. A simulation model of canal systems’ control based on MATLAB was constructed, which consisted of 7modules:physicalmodel establish of canal systems, steady flow state profile calculation,feedforward control module, feedback control module, gate discharge calculation, gate opening transformation and unsteady flow calculation.Among the models,energy equations and de Saint-Venant system of equations were used to compute the constant flow and unsteady flow,and the canal control system was designed which regarded flow rate as the feedforward and the water level as the feedback. Relying on the imulation model of canal systems’ control, we optimized the controller parameter aimed at different nondimensional performance indicators, and conducted the comparison between each other. The simulation proved that the optimal values of indicators had high consistency in the order of magnitude with little concern to the canal scale. For example, the optimal NIAQ (nondimensional integrated absolute discharge change) of both canal systems was 10-5. So this series of indicators could be used to compare the performance of different canal systems. However, due to the different optimization effect of single indicator, pursuing the extreme of any single indicator might result in an unbalanced system. Through the analysis of genetic relationship and representativeness among the series of dimensionless performance indicators, a general indicator (GI) was given based on the water level deviation, flow rate changes and transition time with weight. And as far as we’re concerned, the control performance was fit for our requirement when the value of GI was no more than 10-3in magnitude. The simulation results showed that this aimed GI could stabilize the system and balance all dynamic performances of canal systems well compared with a signal indicator. What was more, we studied the flow and water level procedure lines the canal systems showed under different controller parameters by controlling variable. And we discussed the relationship between proportional-integral-derivative (PID) controller parameters and performance indicators. There existed an insensitive range in which the proportional gain could control the flow rate smoothly in pure proportional (P) controller (proportional gainwas smaller than 4 in No.1 canal system, and smaller than 15 in No.2 canal system),and the integral time had a similar effect on water level in proportional-integral (PI) controller. Thus the optimizing method of finding a robust controller was proposed preliminarily: searching the intersection of controller parameters which worked well under different conditions. The series of non-dimensional indicators and GI proposed by this paper can be used to evaluate different canal control systems and different controllers, which can be used as benchmark while designing a new canal control system. This work suggests quite promising solution for the operation of a large number of water delivery systems and irrigation district canal networks in China.

canals; automation; optimization; dynamic performance indicators; optimization of PI controller parameters; numerical simulation;nondimensionalize

10.11975/j.issn.1002-6819.2018.07.012

S274.2；TV91

A

1002-6819(2018)-07-0090-10

管光華，鐘 錁，廖文俊，肖昌誠，蘇海旺. 基于無量綱性能指標的渠系控制器參數優化[J]. 農業工程學報，2018，34(7)：90－99. doi：10.11975/j.issn.1002-6819.2018.07.012 http://www.tcsae.org

Guan Guanghua, Zhong Ke, Liao Wenjun, Xiao Changcheng, Su Haiwang. Optimization of controller parameters based on nondimensional performance indicators for canal systems[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(7): 90－99. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.07.012 http://www.tcsae.org

2017-11-01

2018-02-27

國家自然科學基金項目(51439006)；國家重點研發計劃(2016YFC0401810)

管光華，博士，副教授，主要研究方向為渠道系統自動化運行調度理論與技術，灌區量水理論與方法，灌排工程新結構。 Email：GGH@whu.edu.cn。

中國農業工程學會會員：管光華（E041700033M）