基于粒子群算法的轎車車身多學科優化設計?

劉 釗，李 晗，朱 平

前言

轎車車身結構設計是一個集汽車碰撞安全性、振動、噪聲和舒適性為一體的復雜系統優化設計問題。在其設計過程中，設計變量多、非線性程度強，學科間耦合關系復雜，常用的多學科優化策略和優化算法無法有效尋得可行的優化解。

為有效解決車身多學科優化設計問題，國內外學者進行了一系列的探索。文獻[1]中在同時考慮材料替換、碰撞性能和NVH約束的情況下對鎂材料車身結構進行了多學科優化設計，并運用SQP進行序列求解，獲得材料替換后較為優異的車身零部件厚度分布。文獻[2]中提出基于近似建模技術的解決大規模工程問題的多學科優化流程，并將其運用到整車結構開發流程中，顯示了該方法的先進性。文獻[3]中針對一款商用車身首先進行拓撲概念設計，然后進行基于近似模型的多學科結構變量優化設計。采用全局靈敏度分析方法來減少整體結構優化變量的個數，通過算例分析證明其多學科優化設計流程的可行性。文獻[4]和文獻[5]中結合協同優化與多目標遺傳算法，綜合考慮側撞安全、白車身模態和靜態彎曲剛度等性能響應進行車身結構輕量化設計。文獻[6]中通過多學科優化過程找到白車身零件形狀、尺寸、位置和厚度各參數間的最佳組合。文獻[7]中運用協同優化方法，結合可靠性優化方法提高優化結果的可靠性。文獻[8]中考慮自卸車貨箱線性靜力和振動模態，運用多學科優化設計方法進行輕量化設計。文獻[9]中針對汽車轉向盤骨架性能進行結合協同優化和近似建模技術的性能優化設計。

由國內外學者的研究可知，多學科優化設計在汽車中的應用靈活，常采用近似建模、變量篩選和靈敏度分析等方法來降低問題復雜程度。一體式優化方法運用較多，因其避免了學科間共享變量的處理問題，但子學科自主性較差，無法針對各子學科特點進行相應的優化處理，基于兩步式的多學科優化方法如協同優化算法有待研究。此外，優化算法選擇單一，雖有提及優化算法求解問題，但并未針對單獨子學科進行考慮學科特點的優化運算。本文中針對車身多學科優化設計問題，提出基于靈敏度分析的數據挖掘技術，辨識問題的優化區域，形成考慮優化問題特點的粒子群算法流程，有效提高了粒子群優化算法解決約束優化問題的能力，結合加強多學科協同優化理論，形成了基于改進粒子群算法的轎車車身多學科優化設計體系，并通過實際工程案例驗證了該方法的有效性。

1　約束條件下的粒子群優化算法

1.1　粒子群優化算法

粒子群優化算法是一種基于群體智能的進化計算(evolutionary computation)技術，其思想來源于人工生命和進化計算理論。粒子群優化算法是以模擬鳥群的群體智能為特征，以求解連續變量優化問題為背景的一種優化算法，最早由Kennedy等學者受到鳥群覓食行為的啟發而提出[10]。粒子群優化算法采用實數求解，且需要調整的參數少，易于實現，是一種通用的全局優化算法。

1.1.1粒子群優化算法的基本形式

基本的粒子群優化算法中，粒子群由m個粒子組成，每個粒子的位置代表一個優化問題在n維搜索空間中的潛在的優化解。粒子根據以下3條規則來更新自己的狀態:保持自身慣性、按自身的最優位置來改變狀態和按照群體的最優位置來改變狀態。

通常粒子群算法的數學描述為:假設在一個n維的搜索空間中，由m個粒子組成的種群χ＝{x1，x2，…，xm}，其中第 i個粒子的位置為 xi＝ (xi，1，xi，2，…，xi，n)T，其速度為 vi＝(vi，1，vi，2，…，vi，n)T。個體極值為 pi＝(pi，1，pi，2，…，pi，n)T，種群的全局極值為pg＝(pg，1，pg，2，…，pg，n)T。 粒子在找到上述兩個極值后，就根據速度更新公式和位置更新公式來更新自己的速度和位置:

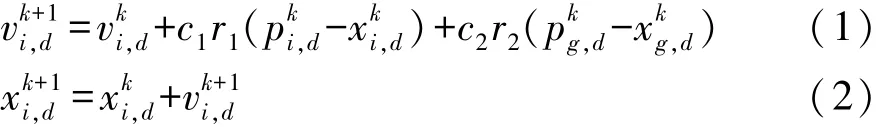
式中:c1和c2為學習因子或加速常數；r1和r2為介于[0，1]之間的隨機數；vki，d和 xki，d分別為粒子 i在第 k次迭代中第d維的速度和位置；pki，d為粒子 i在第 d維的個體極值位置；pkg，d為群體在第d維的全局極值的位置。

1.1.2粒子群優化算法流程

粒子群優化算法流程如圖1所示。

圖1　標準粒子群算法流程圖

1.2　約束處理方式分析

粒子群優化算法優化過程中模擬鳥群覓食行為可有效地尋得全局最優解，效率高、穩定性好。但其開發初期主要針對無約束優化問題，而現實的工程問題多為約束優化問題，約束的引入會對優化進程產生較大的影響，進而影響該方法的應用。粒子群算法優化過程中常用的兩種約束為邊界約束與函數約束。

1.2.1邊界約束

邊界約束是指優化問題給定的設計變量尋優范圍。如果一個優化問題含有邊界約束，當粒子運動處于設計邊界外時需要進行適當的處理，特別是那些優化解處于靠近邊界的可行區域內的問題，邊界約束的處理方式對其優化求解影響較大。文獻[11]中系統性地研究了不同的邊界約束處理方法，通過大量的數學實驗分析，得出邊界反射方式與粒子速度賦值為0適用于大多數測試函數。邊界反射處理方法(reflect method)將位置在設計域以外的粒子基于設計邊界反射回到設計域內，其原理如圖2所示。

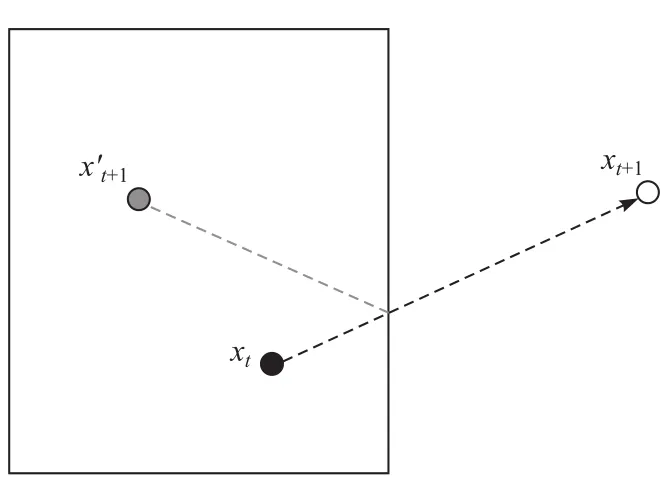
圖2　邊界反射方法

1.2.2函數約束

函數約束在實際優化問題中經常遇到，其處理方式的選擇對優化問題的求解有較大的影響。目前，懲罰函數方法在約束問題處理中運用最為廣泛，其主要思想是將優化問題的約束函數進行轉換，形成一系列的無約束優化問題。本研究中采用最普遍的非靜態懲罰函數法來處理約束優化問題[12]。

通常包含懲罰函數的方程為

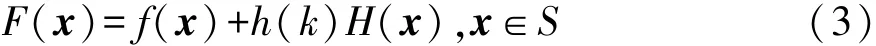
式中:f(x)為約束優化問題的初始目標函數；h(k)為懲罰修正值，k為當前的代數；H(x)為懲罰因子。

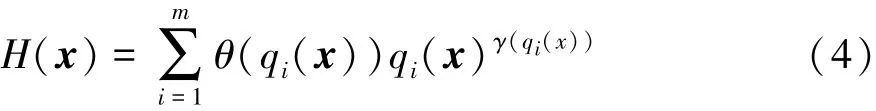
式中:qi(x)＝ max{0，gi(x)}，i＝ 1，…，m；θ(qi(x))為多級分配函數[13]；γ(qi(x))為懲罰函數的指數；gi(x)為懲罰函數。

本文中懲罰函數的參數設置與文獻[12]中相同。 若 qi(x)＜1，則 γ(qi(x))＝ 1，否則 γ(qi(x))＝2。 若 qi(x)≤0.001，則 θ(qi(x))＝ 10；若 0.001＜qi(x)≤0.1，則 θ(qi(x))＝ 20；若 0.1＜qi(x)≤1，則θ(qi(x))＝ 100；若 qi(x)＞1，則 θ(qi(x))＝ 300。 優化問題中h(k)＝k k。

1.3　基于靈敏度分析的優化域識別方法

對于復雜的工程實際應用問題，其優化數學模型的形態復雜，優化求解困難，優化結果精度達不到要求。目前一般的算法對優化初始位置的攝取依賴性較大，對于高維復雜工程優化問題，特別是車身碰撞工況這種強非線性的復雜優化問題，傳統優化算法難以獲得有效全局最優解，需要采用先進優化算法進行尋優求解，而為獲得更好的效果，須進行相應粒子群位置的優化。

1.3.1靈敏度分析技術

為得到初始求解合理的粒子分布區域，需要針對具體的問題的優化目標，運用分類與回歸樹(CART)數據挖掘技術針對可行的優化區域進行辨識。通過靈敏度分析可決定參數對系統或模型的影響程度。目前最常用的全局靈敏度分析方法為Sobol法。

Sobol靈敏度分析方法是一種基于方差的蒙特卡羅方法。定義一個k維的單元體Ωk作為輸入變量(因素)的空間域:

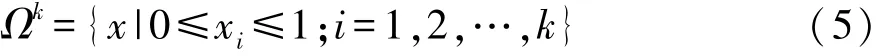
Sobol方法的核心思想是將函數f(x)分解為子項之和:

根據統計學相關知識，模型輸出f(x)的總方差為

各階子項的方差稱為各階偏方差，即s階偏方為

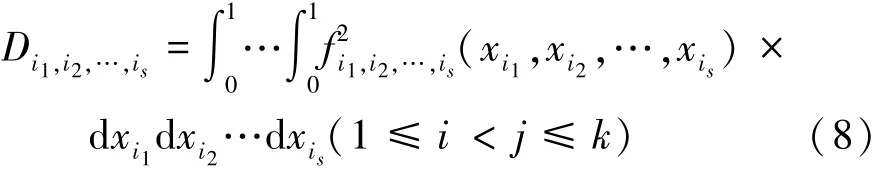
總方差等于各階偏方差之和:

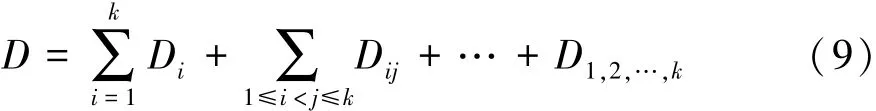
將各階靈敏度系數定義為各階偏方差與總方差的比值，則 s階靈敏度 Si1，i2，…，is為

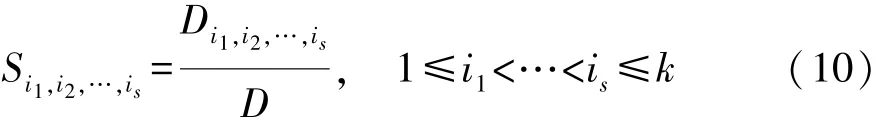
式中:Si為因素xi的1階靈敏度系數，表示xi對系統輸出的主要影響；Sij(i≠j)為2階靈敏度系數，表示兩因素之間的相互影響；依次類推，S1，2，…，k為 k 階靈敏度，表示k個因素之間的相互作用。

在Sobol靈敏度分析方法中，各積分可由蒙特卡羅法求出。因此f0，D和Di可通過蒙特卡羅估計求得:

1.3.2基于靈敏度分析的優化域識別流程

針對約束優化問題影響主因的數據挖掘流程如圖3所示。

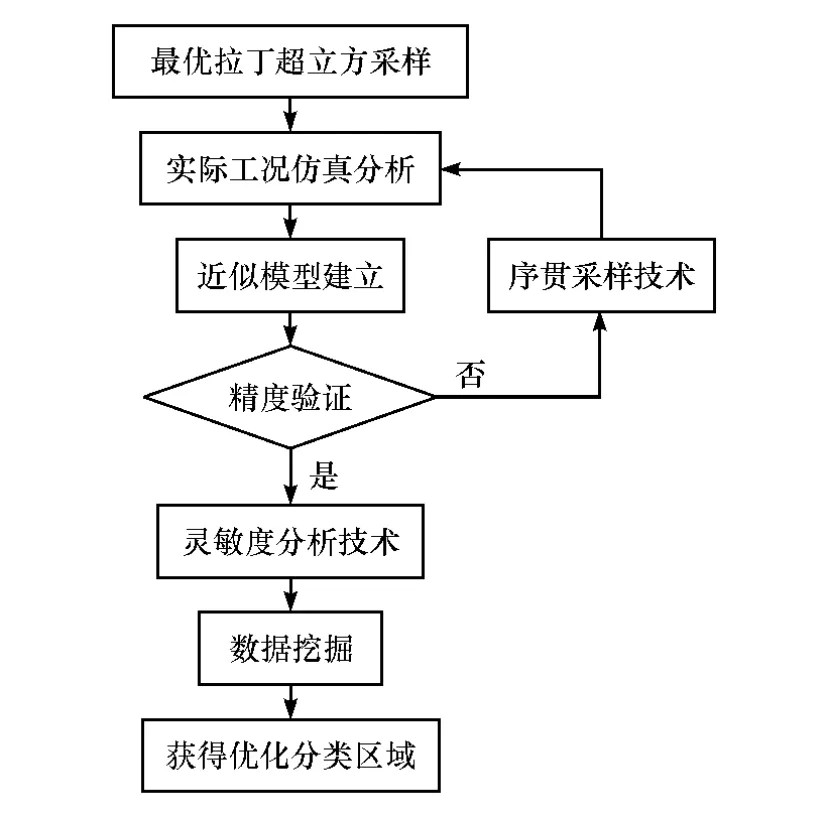
圖3　基于靈敏度分析的數據挖掘方法

具體步驟如下:

(1)針對具體的實際工程優化問題，進行設計域內的最優拉丁超立方采樣，采樣技術選擇基于加強進化算法的最優拉丁超立方采樣技術，采樣規模根據實際工況的設計變量個數與問題復雜程度進行；

(2)對實際問題進行有限元仿真分析，輸入步驟(1)中的采樣數據，輸出為優化目標和約束的響應值；

(3)運用步驟(1)和(2)中獲得的問題輸入與輸出建立近似模型，驗證模型精度，如不滿足則通過序貫采樣技術進行近似模型精度提升；

(4)基于滿足精度要求的近似模型進行靈敏度分析，獲得影響問題響應的主要設計變量；

(5)針對優化問題的主要影響變量，運用分類與回歸樹數據挖掘方法(CART)進行數據挖掘，獲得問題的優化設計區域。

1.3.3考慮優化問題特點的粒子群分布控制方法

為能針對具體的優化問題進行更好的尋優求解，開發出考慮優化問題特點的粒子群分布控制方法。主要思想是在通過數據挖掘方法進行設計域分析的基礎上，進行初始粒子群位置的布置。本部分初始粒子群主要由兩部分組成:第一部分采用最優拉丁超立方采樣的方法，保證了粒子群對優化設計空間的覆蓋；第二部分粒子主要分布在由數據挖掘技術分類出的優化區域，該區域考慮了影響問題的主因，通過針對主要設計變量進行相應的數據挖掘，獲得與具體優化問題相適應的分類區域。隨后運用粒子群優化算法進行尋優運算，具體流程見圖4。

圖4　考慮學科特點的粒子群方法

該方法通過對設計域的初始探索，更有效地指導粒子在設計空間中的分布，在保證了粒子對整個設計域探索的同時，重點將粒子分配在可能的優化區域，進而提高粒子種群針對特定優化問題的探索能力，提升粒子群算法的尋優精度。

2　加強協同多學科優化方法

傳統的協同優化方法(CO)開發以來，已被成功運用在航空航天和交通運輸等領域，但其在求解過程中會遇到諸如存在奇異解、不收斂等缺陷。因此，文獻[14]中提出加強協同優化算法(ECO)[14]，該算法的核心思想是將各子系統之間的約束模型進行相互共享，在一個子系統優化過程中，考慮到其余子系統對該子系統的影響，這樣可以避免子系統級優化時為了尋找合適的共享變量造成的求解困難。ECO方法針對系統級優化和子系統級優化結構進行了相應的修改。

系統級優化器一般的表達形式為

式中:z為系統級賦予共享變量的目標值；x?為子系統優化過程中尋得的與系統級優化目標最接近的問題解。原始的協同優化算法為各子學科級的優化提供了很大的學科自由度，每個子系統可根據自己的學科特點選擇相適應的優化技術。但每一個學科對其余子學科的學科特點和優化偏好并不清楚。各子學科之間信息的傳遞只能通過主系統進行間接傳遞，這就要求系統級優化器需要承擔共享變量的選擇任務。子系統級優化器承擔大部分的設計決策任務，其目標函數包含3個部分:系統優化目標的二次方程、檢驗兼容性的二次方程和一系列的松弛參數。其約束包含子系統局部約束和由于其余學科的耦合關系而產生的約束。子系統接收由主系統傳遞的目標(z)和作為參數的約束模型系數(?g(j)/?xs)。子系統反饋響應目標(x?s)，子系統級優化器數學表達為

式中:x為子系統獨立的共享變量；xL為局部變量；xs＝[x，y]為與多個子系統相關的共享變量；y為耦合變量；s為松弛系數，保證子系統問題求解的可行性；z為參數，由系統級優化器提供，作為子系統目標；λC為兼容性懲罰系數；λF為可行性懲罰系數；F～為問題目標的二次方程組模型；g(i)為子系統i的局部約束；g～(j)為子系統j的線性約束模型。

3　車身側圍結構輕量化設計

車身側面結構相對簡單，在碰撞過程中，其結構的變化將直接影響到乘員艙內駕乘人員的生命安全，因此側面碰撞工況是其設計時需要重點考慮的一個工況。同時側圍結構對整車的剛度模態變化影響較大，因此也需要在設計時進行重點考核，所以在車身側圍結構設計時需要同時考慮碰撞工況和車身剛度模態工況，是一個典型的多學科優化問題。本文中將選它作為應用案例，結合協同多學科優化設計方法，驗證研究中提出的考慮優化問題特點的粒子群分布控制方法的合理性和實用性。

3.1　優化設計問題

整車側面碰撞有限元模型包含詳細的白車身、底盤和動力總成有限元模型，單元平均尺寸為10mm，殼單元1 005 019個，實體單元22 575個，梁單元7 718個。轎車側面碰撞仿真模型如圖5所示。

圖5　側面碰撞仿真模型

根據GB 20071—2006《汽車側面碰撞的乘員保護》的法規要求，質量為950kg的移動壁障車以50km/h的速度呈90°沖擊轎車駕駛員側，移動壁障車的對稱中面通過駕駛員座椅的R點，仿真時間為80ms。考慮的性能指標為:假人下肋骨最大變形量、B柱最大變形速度、車門最大變形速度、假人腹部作用力、假人盆骨作用力。選取與側面碰撞最相關的車身側面15個板件的厚度作為設計變量，如圖6所示。

圖6　側面碰撞設計變量

建立考核車身剛度和模態的白車身有限元模型，如圖 7所示，白車身骨架共有 275個零件，351 722個單元，其中三角形單元15 851個，占單元總數比例4.51%，根據有限元網格劃分規則，可知建立的車身骨架有限元模型精度可靠，可用于后續的仿真運算。

圖7　剛度、模態優化設計變量

車身剛度包括彎曲剛度和扭轉剛度兩個指標，主要研究白車身結構在受到外界載荷作用下結構抵抗變形的能力。對于車身剛度和模態工況來說，設計變量較多，為降低運算成本，運用靈敏度分析技術獲得其設計變量中影響較大的20個變量作為優化設計變量進行后續的優化運算。

綜合車身側面碰撞工況和車身剛度模態工況的幾種性能指標，具體指標和約束要求如表1所示。基于驗證后的仿真模型，進行針對每一個碰撞工況的優化設計域識別。首先是針對仿真工況進行近似模型建模。根據各自工況的設計變量個數進行最優拉丁超立方采樣，建立與之相對應的近似模型，并驗證模型精度，獲得滿足精度要求的數學模型。其中，側面碰撞工況設計變量15個，訓練樣本120個，測試樣本20個；白車身剛度和模態工況設計變量20個，訓練樣本100個，測試樣本20個。

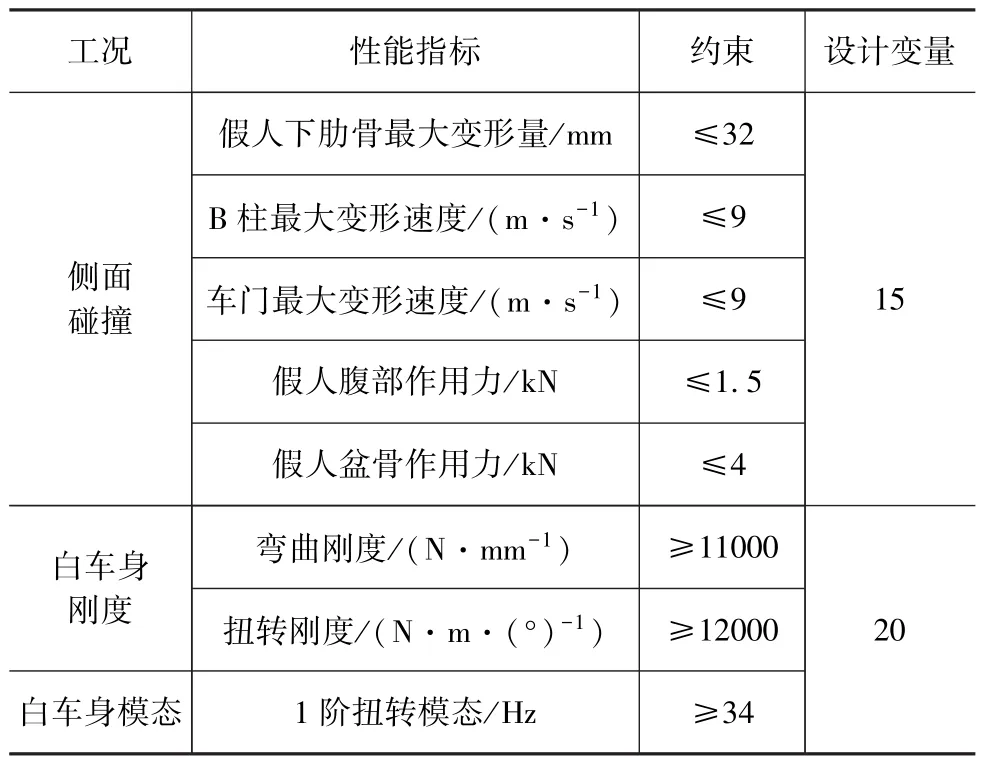
表1　工況描述

根據加強協同多學科優化方法，建立兩學科系統。本例中優化目標為質量最小，優化目標可方便地分配到各個子學科，且各學科間只存在共享變量，不存在狀態變量(學科間耦合變量)，因此問題的形式比較明確。

系統級優化主要平衡學科間的一致性，其形式為

在子學科系統中，共享變量有兩個，子系統目標形式需加入保證學科一致性的多項式，子系統優化問題的數學模型如下。

(1)側面碰撞

式中:Mside(xs)為側面碰撞工況輕量化分目標；λC∑(xside＿s-z)2為一致性約束條件。其約束為側面碰撞工況中需要考慮的各約束指標。

(2)車身剛度和模態

式中:Mstiff(xs)為側面碰撞工況輕量化分目標；λC∑(xstiff＿s-z)2為一致性約束條件。其約束為車身剛度和模態工況中需要考慮的各約束指標。

3.2　優化問題設計域識別

基于近似模型，建立靈敏度分析目標值:

運用靈敏度分析技術，分析每個碰撞工況中影響優化問題的主要變量，約束函數因子λ取值均為1。經分析后各工況選取靈敏度排序前5的設計變量如表2所示。

表2　各工況靈敏度分析

3.3　優化與結果分析

本文中提出的多學科優化運用加強協同優化算法進行各個學科耦合關系的構建，運用基于靈敏度的數據挖掘技術進行優化區域辨識，通過合理布置粒子進行基于粒子群優化算法的尋優求解。因本算例中考慮到碰撞和剛度模態兩個學科，對于碰撞工況來說，其優化非線性強，尋優相對困難，故基于多樣性保持機制的改進粒子群算法策略[15]；而對于剛度和模態工況，因其優化問題非線性程度較弱，相對易于求解，故采用標準粒子群算法流程。實驗算例定義為算例1，為驗證本例運用多學科優化方法結構的優勢，設計算例2和算例3兩種對比算例。算例2同樣運用考慮學科特點的優化域挖掘技術，與算例1算法結構相同，但在優化算法選擇上各子學科均采用標準粒子群算法。算例3中在優化運算時不采用優化域挖掘的方法，僅用加強協同優化算法結構，優化求解方法運用標準粒子群算法。

對3種算例結構進行尋優求解，為將數學求解結果轉換為實際工程中可以運用的板厚，對優化結果進行圓整。將圓整后的結果輸入到仿真軟件中進行分析，驗證結構設計結果的正確性。結果如表3所示，算例1完成減質量12.6kg，減質量效果為14.6%；算例2完成減質量 8.1kg，減質量效果為9.4%；算例3完成減質量6.16kg，減質量效果為7.1%。通過對比驗證了本文中提出的多學科優化構架在實際工程中尋優求解的優勢。

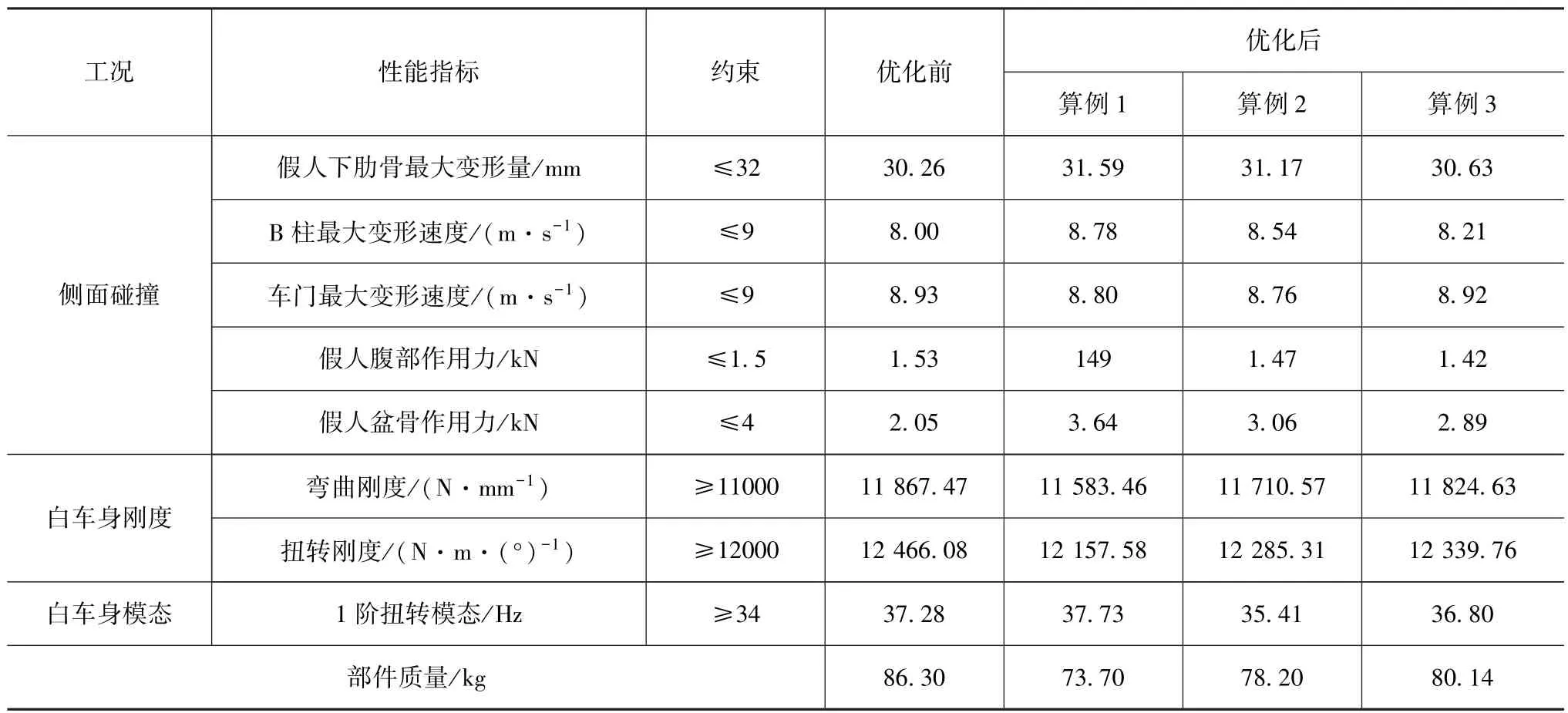
表3　各算例輕量化方案的性能指標狀態

4　結論

(1)針對車身結構多學科優化設計問題，研究了其耦合結構與優化算法運用兩個問題。分析其多學科之間的耦合關系，運用加強協同多學科優化策略，系統級優化主要解決學科一致性問題，各子系統承擔部分問題的優化目標，并通過目標和約束修正考慮不同學科之間的耦合關系，保證學科間的一致性。

(2)考慮不同學科優化問題特性不同，針對具體的問題進行基于靈敏度分析的數據挖掘，獲得問題的優化區域，進而指導粒子群優化算法初始粒子在設計空間中的位置分布，在可能的優化區域，重點布置粒子，提高粒子種群針對特定優化問題的探索能力，提升粒子群算法的尋優精度。

(3)結合加強協同多學科優化理論，基于本文中所提方法，進行轎車車身側面結構輕量化設計優化求解，實現結構最多減質量12.6kg，減質量效果達到14.6%，驗證了本文中所提出方法在實際工程問題中應用的有效性，為實際車身多學科優化設計提供了可借鑒的方法和途徑。

[1] KIANI M，GANDIKOTA I，RAIS-ROHANI M，et al.Design of lightweight magnesium car body structure under crash and vibration constraints[J].Journal of Magnesium&Alloys，2014，2(2):99-108.

[2] RYBERG A B，NILSSON L.A metamodel-based multidisciplinary design optimization process for automotive structures[J].Engineering with Computers，2015，31(4):711-728.

[3] BASTIEN C，PREM A，DICKISON M.Multidisciplinary design optimisation strategies for lightweight vehicle structures[C].LSDyna European Conference，2015.

[4] WANG P，GUANGQIANG W U.Multidisciplinary design optimization of vehicle instrument panel based on multi-objective genetic algorithm[J].Chinese Journal of Mechanical Engineering，2013，26(2):304-312.

[5] 王平，鄭松林，吳光強.基于協同優化和多目標遺傳算法的車身結構多學科優化設計[J].機械工程學報，2011，47(2):102-108.

[6] 史國宏，陳勇，楊雨澤，等.白車身多學科輕量化優化設計應用[J].機械工程學報，2012，48(8):110-114.

[7] 姜武華，王其東，何煒，等.基于可靠性的車橋結構多學科優化[J].汽車工程，2012，34(12):1136-1140.

[8] 史朝軍，張勝蘭，楊啓梁.自卸車貨箱多學科優化設計[J].湖北汽車工業學院學報，2013，27(3):10-14.

[9] 李鐵柱，李光耀，周澤，等.汽車轉向盤骨架性能的多學科設計優化[J].汽車工程，2014，36(3):378-382.

[10] KENNEDY J，EBERHART R.Particle swarm optimization[C].IEEE International Conference on Neural Networks，1995.Proceedings，1995:1942-1948.

[11] BANBURY J.Experimental analysis of bound handling techniques in particle swarm optimization[J].IEEE Transactions on Evolutionary Computation，2013，17(2):259-271.

[12] YANG J M，CHEN Y P，HORNG J T，et al.Applying family competition to evolution strategies for constrained optimization[C].Evolutionary Programming Vi， International Conference，Ep97， Indianapolis， Indiana， Usa， April 13-16，1997， Proceedings.DBLP，1997:201-211.

[13] HOMAIFAR A，QI C X，LAI S H.Constrained optimization via genetic algorithms[J].Simulation Transactions of the Society for Modeling&Simulation International，2010，62(4):242-253.

[14] ROTH B，KROOI.Enhanced collaborative optimization:application to an analytic test problem and aircraft design[C].Aiaa/issmo Multidisciplinary Analysis and Optimization Conference，2006.

[15] LIU Z， LU J， ZHU P.Lightweight design of automotive composite bumper system using modified particle swarm optimizer[J].Composite Structures，2016，140:630-643.