順層巖體各向異性對隧道地震響應的影響

胡鴻運，周曉軍，汪精河

(1.西南交通大學 土木工程學院，四川 成都　610031；2.西南交通大學 交通隧道工程教育部重點實驗室，四川 成都　610031；3.蘭州交通大學 甘肅省道路橋梁與地下工程重點實驗室，甘肅 蘭州　730070)

大量隧道震害表明，隧道穿越地層的地質條件、巖層結構等對隧道結構的地震響應影響極大[1-2]，例如在5.12汶川8.0級地震震害調查中發現，圍巖軟硬互層的隧道破壞較硬巖隧道嚴重[3]。順層巖體隧道(即巖層走向與隧道軸線平行、巖層傾向與隧道軸線垂直的情形)是典型的層狀巖體隧道，與均質巖體隧道相比，順層巖體隧道地震響應的主要特征之一是襯砌結構承受顯著不對稱的地震荷載，襯砌內力也顯著不對稱或非反對稱(非反對稱是指左右對稱位置內力的數值不等、方向相反)[4]，這是由順層巖體的橫觀各向同性而產生的。但近年國內外相關研究通常將隧道圍巖假定為各向同性介質[5-15]，這無法反映上述不對稱性或非反對稱性，因此，應對順層巖體隧道地震響應的規律進行研究。

為此，本文基于順層巖體橫觀各向同性的彈性本構關系(因在極短期的迅速變化的動力作用下，巖體主要表現為彈性[16])，應用黏彈性邊界的時域波動理論，提出順層巖體中二維平面地震波從隧道底部入射時的輸入方法。以某順層巖體高速鐵路隧道為工程背景，采用ANSYS軟件進行地震時隧道動力響應的數值模擬分析，研究qP波和qSV波入射時巖層各向異性強度對隧道地震響應不對稱性或非反對稱性的影響。

1　材料參數及計算模型

1.1　襯砌參數

本文以某典型開挖斷面的高速鐵路深埋隧道為研究對象，如圖1所示，隧道開挖最大寬度為15 m。

圖1　隧道開挖斷面(單位：mm)

隧道二次襯砌：厚度為600 mm，C35混凝土，配筋率為0.35%，彈性模量為31.5 GPa，泊松比為0.2，重度為25 kN·m-3。為更清晰地觀察順層巖體隧道地震響應的特征，略去加固層和初期支護。

1.2　順層巖體參數

為便于對比分析，根據順層巖體各向異性強度依次增強的規則，即巖體Thomsen參數[17]中表征橫觀各向同性介質各向異性強度的3個無量綱因子ε，γ和δ(以及ε-δ)的單調性一致[18]且增幅均勻的規則，設定有5組順層巖體，分別標記為D1， D2，…，D5，其參數詳見表1。

表1　地層參數表

1.3　計算模型

采用ANSYS軟件建立平面有限元模型，以隧道中心為中心截取1 000 m×1 000 m的正方形區域進行離散，順層巖體采用plane42單元、襯砌采用beam3單元、黏彈性邊界采用combin14單元模擬。積分步長為0.01 s。黏彈性邊界彈簧—阻尼參數的計算詳見文獻[4]，其中法向修正系數αN與切向修正系數αT分別取1.0和0.5[19]。

地震波的總波場僅考慮入射波場和隧道反射波場，并采用在有限計算區域4個邊界面上設置近似黏彈性邊界的方法模擬，其中，隧道反射波被黏彈性邊界自然吸收。因為，根據地震波動理論可知，地震波傳播到地面時會產生反射，所以地震波的總波場為自由波場(即入射波場)和散射波場(即地面反射波場和隧道反射波場)的線性疊加[20]。但由于山嶺隧道所處場地的地面起伏不平，所以是極不規則而復雜的反射面，導致順層巖體隧道所處場地的地面反射波場亦極不規則且高度依賴于地面輪廓曲線，即具有特殊性；相反，自由波場和隧道反射波場卻具有一般性。因此，總波場僅考慮入射波場和隧道反射波場。

地震波對隧道的入射位置有可能在隧道的任何位置，但當地震波由隧道底部入射時，準縱波qP的縱波分量平行于隧道橫斷面對稱軸，準橫波qSV的橫波分量垂直與隧道橫斷面對稱軸，隧道襯砌關于斷面對稱軸對稱，這可以有效地呈現因巖層各向異性而產生的襯砌響應不對稱性或非反對稱性，進而根據響應的不對稱性或非反對稱性研究巖層各向異性對隧道地震響應的影響，因此，設定地震波由隧道底部入射。

由此建立的計算模型如圖2所示。有限元模型中隧道襯砌單元劃分及編號如圖3所示，其中A—H為位移監測點。

圖2　平面有限元模型示意圖

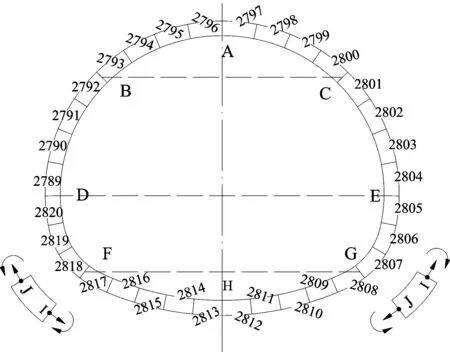
圖3　襯砌單元編號及監測點

2　地震波參數

選取汶川地震時的臥龍波，提取其中振動最劇烈的10～21 s時段的波段，進行濾波和基線校正，得到的位移時程和速度時程如圖4所示，將其作為輸入模型的地震波。

圖4　入射波的位移和速度時程曲線

3　順層巖體中地震波的輸入方法

3.1　順層巖體中地震波的波動特征

1)波動的平面應變特征

根據文獻[21]可知，當地震波入射方向垂直于順層巖體隧道軸線時(見圖2)，則qP波或qSV波僅在平面oxy內波動。因此巖體以及隧道的動力響應為平面應變問題，即在z軸方向上巖體以及隧道的應變始終為0。

2)各坐標系的空間關系

根據計算需要引入多個坐標系，其空間關系如圖5所示。圖5中：ox0y0z0為巖層本構坐標系；oxryrzr為引用文獻[21-22]坐標系；oxyz為總體坐標系；平面S1S2S3S4為巖層層面；地震波傳播方向的極化角(即傳播方向與zr軸正向的夾角)θ=π，方位角(即從正zr軸來看自xr軸按逆時針方向轉到傳播方向在oxrzr平面內投影所轉過的角)φ=0；M為巖體范圍內任一質點；εy為正應變；γxy為剪應變；θ0為巖層傾角，即橫觀各向同性介質對稱軸與zr軸正向的夾角，從正yr軸來看順時針方向為正。

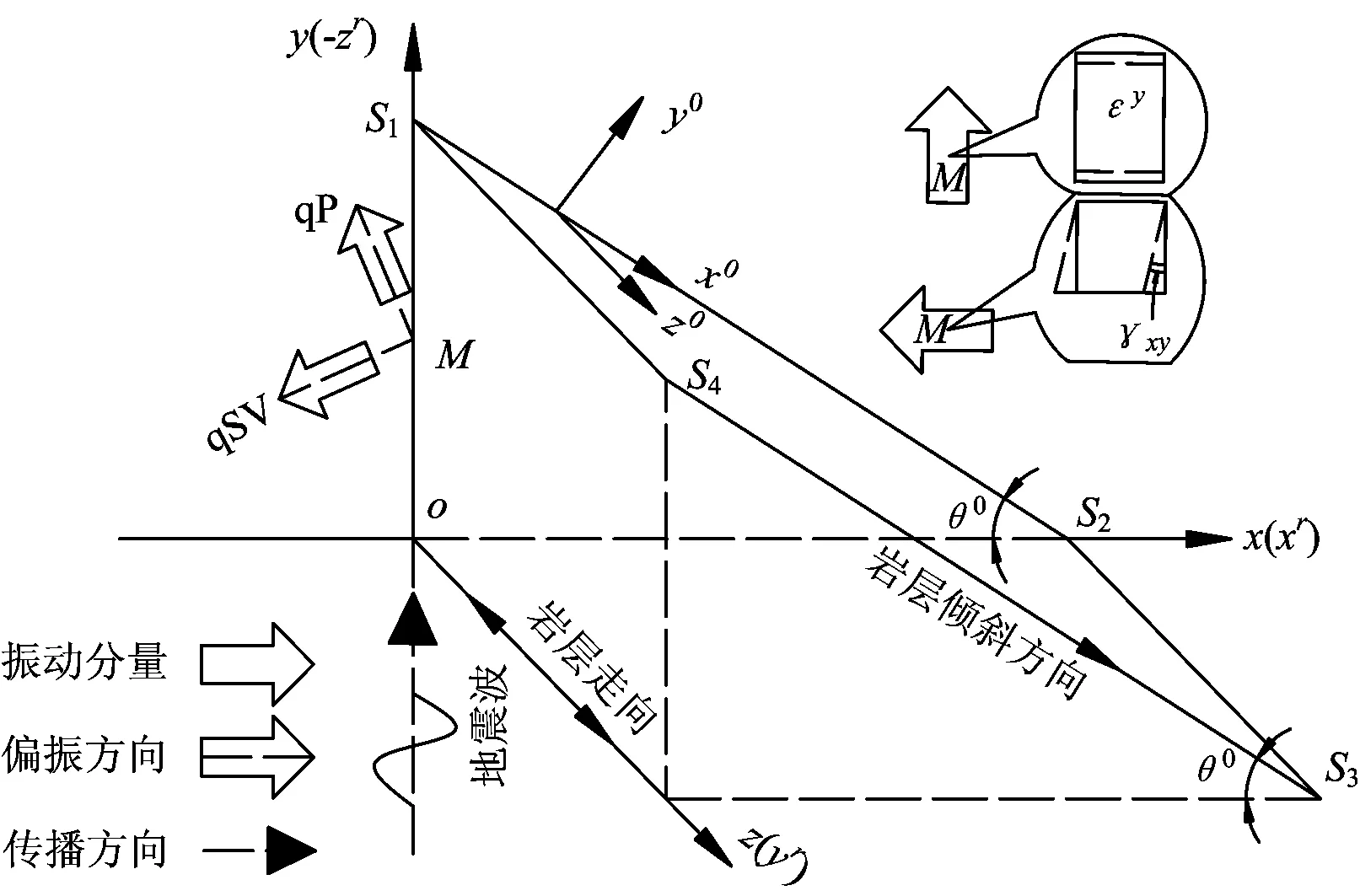
圖5　質點振動方向與應變

3)偏振方向和相速度

在坐標系oxryrzr中，可知地震波偏振向量的精確通解[21]，以及地震波相速度的精確解[22]。

3.2　基于黏彈性邊界的地震波輸入模式

將基于黏彈性邊界的地震動輸入轉化為人工邊界結點上等效荷載的公式[23]為

(1)

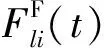
3.3　計算人工邊界上內行場的位移和速度

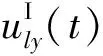
(2)

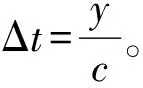
式中：Δt為入射波從零時刻波陣面(黏彈性下邊界)傳播到人工邊界結點l所需的時間，s；y為人工邊界結點l到下人工邊界的距離，m；c為cp或csv，其中cp為入射qP波的波速，csw為入射qSV波的波速，m·s-1。

3.4　人工邊界上的等效結點力

3.4.1彈性矩陣的轉換

計算中須把坐標系ox0y0z0下的彈性矩陣根據bond變換(Winterstein，1990)[18]轉換為總體坐標系oxyz下的彈性矩陣。

3.4.2平面波入射時的應變—應力

根據波動特征可知[21]，波場中某質點M的偏振方向如圖5所示，qP波偏振方向與傳播方向并不平行，qSV波偏振方向與傳播方向并不垂直；又因為介質屬于線彈性的，所以，質點振動量可分解為沿x軸和y軸的分量，見圖5。

1)入射波引起的應變—應力

根據彈性動力力學，并結合文獻[5]中幾何方程推導過程可知，當入射波沿y向傳播時，y向上的位移分量u0y所引起的應變為拉壓應變εy，而x向上的位移分量u0x所引起的應變為剪應變γxy，也見圖5。應變的計算公式為

(3)

相應的應力計算公式為

(4)

式中：σx為x向的正應力；σy為y向的正應力；τxy為剪應力，N·m-2；c11，c14，…，c44為橫觀各向同性介質在總體坐標系oxyz下的剛性系數，N·m-2。

對于式(3)：當qP波入射時，由于qP波在垂直于傳播方向上的分量以橫波的波速傳播，即qP波會不斷激發新的橫波，而被激發的橫波又與縱波交織在一起，橫波和縱波的耦合會導致研究者難以觀察qP波的縱波分量所產生的地震響應的規律，且該橫波分量較小，故在模擬qP波地震響應時，略去其橫波部分，即令γxy=0；當qSV波入射時，由于qSV波在平行于傳播方向上的分量以縱波的波速傳播，即qSV波會不斷激發新的縱波，而被激發的縱波又與橫波交織在一起，橫波和縱波的耦合會導致研究者難以觀察qSV波的橫波分量所產生的地震響應的規律，且該縱波分量較小，故在模擬qSV波地震響應時，略去其縱波部分，即令εy=0。

3.4.3人工邊界上等效結點力的計算

最后，計算不同平面地震波作用下隧道結構的響應時，針對不同的平面波類型，將式(4)中各人工邊界結點l的應力與其所代表的邊界面積As相乘，即可得出該點的等效結點力。

4　qP波入射時巖層各向異性對隧道地震響應不對稱性的影響

4.1　qP波入射工況設計

選取qP波的10種工況進行計算，各工況的參數詳見表2。其中工況編號約定：以qP-D1-30°為例，qP為地震波類別，D1為地層標號，30°為巖層傾角；其余類推。從表2可知：從D1到D5組順層巖體，各工況橫波分量的偏振向量依次增大，但均小于0.22，所以將其略去，僅采用縱波分量的偏振向量進行計算。

表2　qP波入射時各工況的相速度和坐標系oxy下偏振量

4.2　彎矩包絡結果與分析

各工況下隧道彎矩的包絡圖如圖6所示。由圖6可知：同一巖層傾角時，各工況下隧道彎矩包絡圖極為相似；且傾角為30°時，左拱腳彎矩大于右拱腳，而傾角為60°時，卻是右拱腳彎矩大于左拱腳。又據拱腳彎矩包絡數據可知，各工況拱腳彎矩極值，數值不等，時間不同。

分析該不對稱性與巖層各向異性的關系，消除地震響應幅度隨巖層強度降低而增強所產生的影響，定義參數左右彎矩差之比δW，其計算公式為

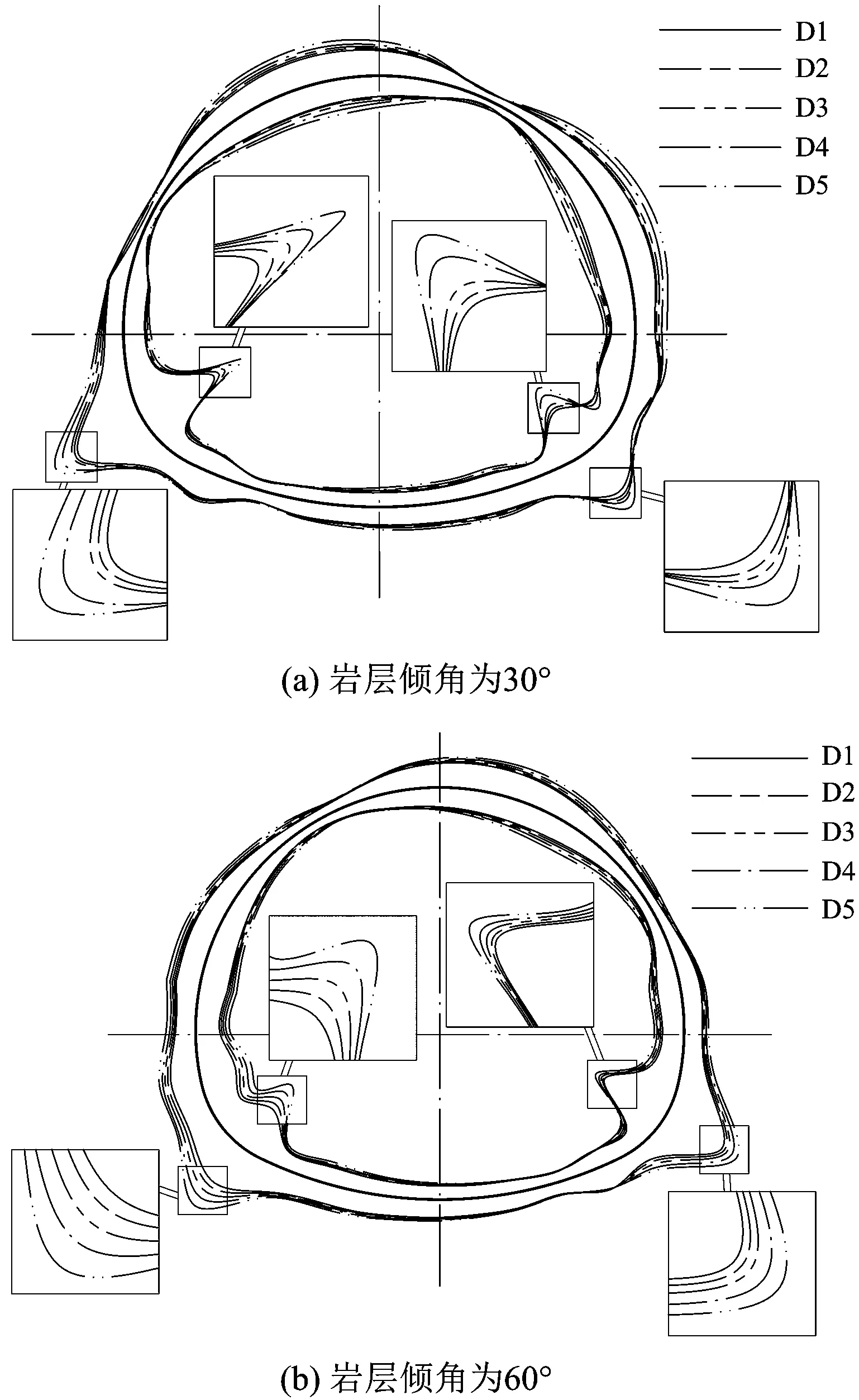
圖6　qP波入射時各工況下的隧道彎矩包絡圖

(5)

式中：ML和MR分別為左、右拱腳的彎矩。

取同時刻拱腳彎矩的極大值和極小值，采用式

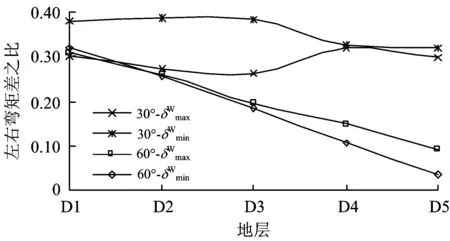
圖7　不同地層的左右彎矩差之比(包絡)

圖8　不同地層的左右彎矩差之比(同時)

4.3　相對位移結果與分析

斷面內各測點間的相對位移見表3。表3中：dBG為同時刻測點B和測點G之間的相對位移；其余類推；測點間距離相對原始距離變大為正，反之為負。由表3可知：以工況qP-D1-30°為例，在6.68和8.18 s時，其相對位移左右不對稱；在6.68 s時，襯砌在B到G方向處于拉伸狀態，而在C到F方向卻處于壓縮狀態；在8.19 s時，襯砌在B到G方向處于壓縮狀態，而在C到F方向卻處于拉伸狀態；其余工況的規律相同，只是不同地層，數值不同。

表3　相對位移對照表

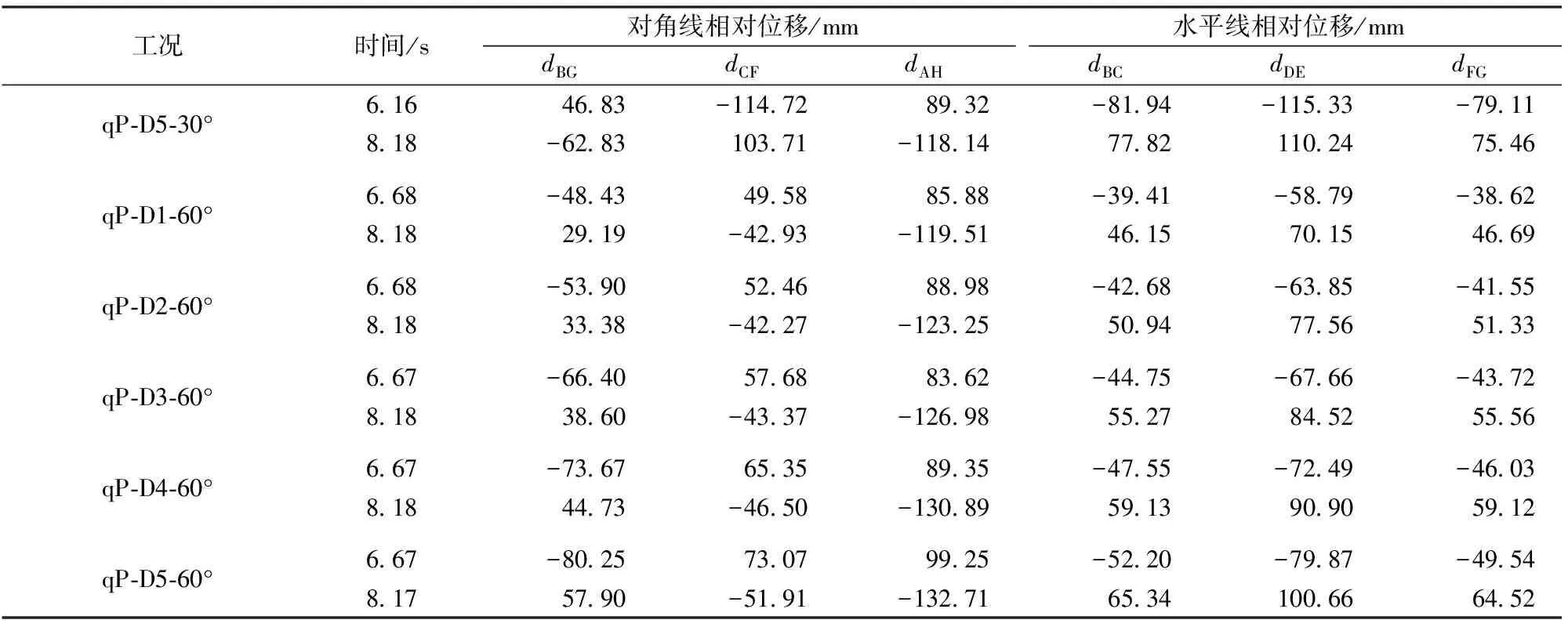
續表3　相對位移對照表

為分析該不對稱性隨巖層各向異性變化的規律，定義參數位移差之比δS，其計算公式為

(6)

圖9　不同地層的位移差之比曲線(同時)

5　qSV波入射時巖層各向異性對隧道地震響應非反對稱性的影響

5.1　qSV波入射工況設計

選取qSV波的10種工況進行計算，各工況的參數詳見表4。從表4可知：從D1到D5組順層巖體，各工況縱波分量的偏振向量依次增大，但均小于0.22，所以將其略去，僅采用橫波分量的偏振向量進行計算。

表4qSV波入射時各工況的相速度和坐標系oxy下偏振量

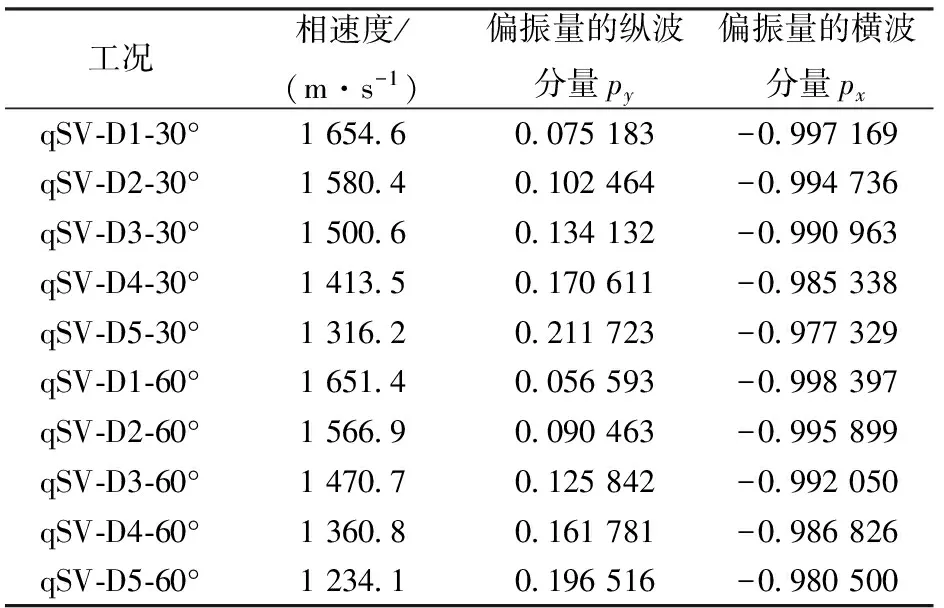
工況相速度/(m·s-1)偏振量的縱波分量py偏振量的橫波分量pxqSV?D1?30°165460075183-0997169qSV?D2?30°158040102464-0994736qSV?D3?30°150060134132-0990963qSV?D4?30°141350170611-0985338qSV?D5?30°131620211723-0977329qSV?D1?60°165140056593-0998397qSV?D2?60°156690090463-0995899qSV?D3?60°147070125842-0992050qSV?D4?60°136080161781-0986826qSV?D5?60°123410196516-0980500

5.2　彎矩包絡結果與分析

各工況下隧道彎矩包絡圖如圖10所示。拱腳彎矩峰值及對應的單元和時間見表5；同時刻拱腳彎矩見表6；彎矩方向垂直紙面向外為正，反之為負。由圖10和表5可知：彎矩極值均位于拱腳處，且數值非反對稱；同一巖層傾角時，包絡圖相似且相近。

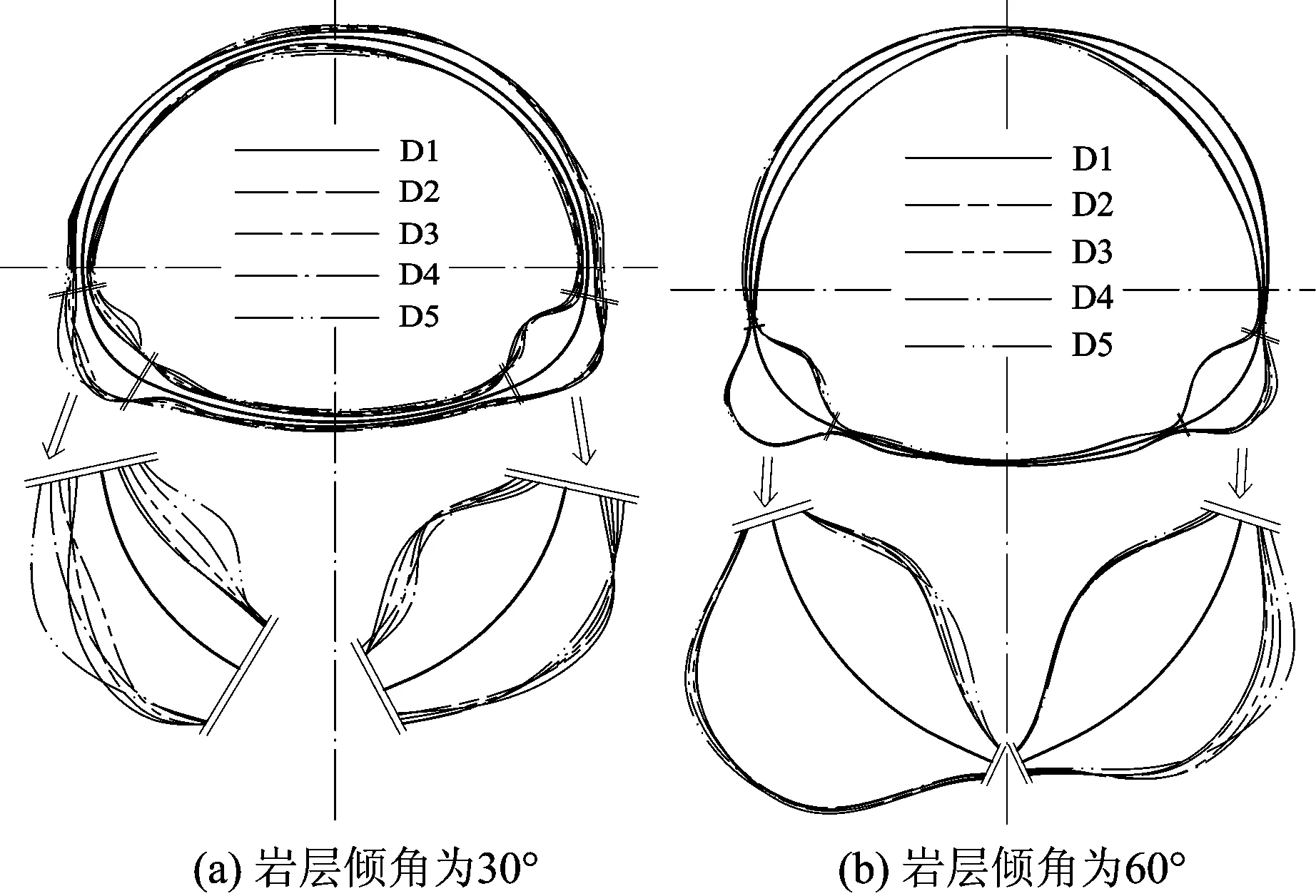
圖10　qSV波入射時各工況下的隧道彎矩包絡圖

工況左拱腳右拱腳單元號彎矩/(kN·m)時間/s單元號彎矩/(kN·m)時間/sqSV?D1?30°28171670548332807-2091958332817-1030785992806119296682qSV?D2?30°28171613108342806-2098128342817-993436012806154168601qSV?D3?30°28171526078352806-2105488352817-1046625162806145815819qSV?D4?30°28171404178372806-2078808372818-138255668280613922482qSV?D5?30°28181955418182806-1923188392818-1829476682806127831824qSV?D1?60°28172090958312807-1674878312818-1689205982806120541598qSV?D2?60°28182079438312807-1637618312818-166520598280612381068qSV?D3?60°28182126208312807-1618428312818-1755006812806135061681qSV?D4?60°28182211108312807-1652408312818-1802556812806135676681qSV?D5?60°28182269248312806-1709428322817-1687498172806158989817

表6　qSV波入射時各工況下同時刻左右彎矩對照表

注：“時間”取左拱腳達到彎矩峰值的時刻；右拱腳的單元號取與左拱腳對稱的單元號。

為分析該非反對稱性隨巖層各向異性變化的規律，定義參數左右彎矩和之比ξW，其計算公式為

(7)

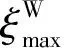
圖11　不同地層的左右彎矩和之比(包絡)

圖12　不同地層的左右彎矩和之比(同時)

5.3　相對位移結果與分析

各工況的相對位移見表7。由表7可知：以工況qSV-D1-30°為例，在5.99和8.33 s時，其相對位移左右非反對稱；在5.99 s時，襯砌在B到G方向處于壓縮狀態，在C到F方向卻處于拉伸狀態，但數值絕對值卻不等；在8.33 s，襯砌在B到G方向處于拉伸狀態，在C到F方向卻處于壓縮狀態，但數值絕對值卻不等；其余工況的規律相同，襯砌相對位移均左右非反對稱，只是不同地層，數值不同。

為分析該非反對稱性隨巖層各向異性變化的規律，定義參數位移和之比ξS，其計算公式為

(8)

取表7中數據，采用式(8)計算位移和之比，繪制圖13。由圖13可知：在巖層傾角為60°時，該左右非反對稱性隨巖層各向異性的增強而增大，近似呈線性關系；而在巖層傾角為30°時，非反對稱性卻并未隨巖層各向異性的增強而增大，而是先減小后增大，呈非線性。可見，隧道襯砌變形隨地層各向異性的變化規律不統一，視巖層傾角而定。

表7　qSV波入射時各工況下的相對位移對照表

注：“時間”的選取同表6。

圖13　不同地層的位移和之比曲線(同時)

6　結　論

(1)地震qP波以平面波從隧道底部入射時，隨著巖層各向異性的增強，同一時刻，隧道地震響應的不對稱性總體上逐漸增大，且服從近似線性關系；但對不同時刻的地震響應包絡而言，卻無明確而統一的規律，視巖層傾角而定。

(2)地震qSV波以平面波從隧道底部入射時，隧道地震響應的非反對稱性隨巖層各向異性的變化缺乏統一明確的規律，視巖層傾角而定。

[1]OKAMOTO Shunzo. Introduction to Earthquake Engineering [M]. 2nd Ed. Tokyo：University of Tokyo Press，1984.

[2]SHARMA S，JUDD W R. Underground Opening Damage from Earthquakes [J]. Engineering Geology，1991，30(3/4)：263-276.

[3]吉隨旺，唐永建，胡德貴，等. 四川省汶川地震災區干線公路典型震害特征分析[J].巖石力學與工程學報，2009，28(6)：1250-1260.

(JI Suiwang，TANG Yongjian，HU Degui，et al. Analysis of Typical Seismic Damages of Highways in Wenchuan Earthquake-Induced Hazard Areas in Sichuan Province[J].Chinese Journal of Rock Mechanics and Engineering，2009，28(6)：1250-1260. in Chinese)

[4]胡鴻運，周曉軍，汪精河. 順層隧道地震響應的波動方法研究[J].巖石力學與工程學報，2017，36(6)：1373-1383.

(HU Hongyun，ZHOU Xiaojun，WANG Jinghe. A Wave Numerical Method for Seismic Response of Tunnels in Bedding Strata[J]. Chinese Journal of Rock Mechanics and Engineering，2017，36(6)：1373-1383. in Chinese)

[5]ST JOHN C M，ZAHRAH T F. Aseismic Design of Underground Structures[J]. Tunnelling and Underground Space Technology，1987，2(2)：165-197.

[6]YOUSSEF M A HASHASH, JEFFREY J HOOK, BIRGER SCHMIDT, et al. Seismic Design and Analysis of Underground Structures[J]. Tunnelling and Underground Space Technology，2001，16(4)：247-293.

[7]ESMAEILI M， VAHDANI S， NOORZAD A. Dynamic Response of Lined Circular Tunnel to Plane Harmonic Waves[J]. Tunnelling and Underground Space Technology，2006，21(5)：511-519.

[8]黃娟,彭立敏,李曉英,等.隧道振動響應研究進展[J].中國鐵道科學，2009，30(2):60-65.

(HUANG Juan, PENG Limin, LI Xiaoying, et al. Progress Made in the Research on the Vibration Response Induced by Trains Running Through Tunnels[J]. China Railway Science，2009，30(2)：60-65. in Chinese)

[9]PARK Kyung-ho,TANTAYOPIN Kullachai,TONTAVANICH Bituporn, et al. Analytical Solution for Seismic-Induced Ovaling of Circular Tunnel Lining under No-Slip Interface Conditions: a Revisit[J]. Tunnelling and Underground Space Technology，2009，24(2)：231-235.

[10]陳磊,陳國興,李麗梅.近場和遠場地震動作用下雙層豎向重疊地鐵隧道地震反應特性[J].中國鐵道科學，2010，31(1):79-86.

(CHEN Lei，CHEN Guoxing，LI Limei. Seismic Response Characteristics of the Double-Layer Vertical Overlapping Metro Tunnels under Near-Field and Far-Field Ground Motions[J]. China Railway Science，2010，31(1)：79-86. in Chinese)

[11]CILINGIR Ulas，GOPAL MADABHUSHI S P. A Model Study on the Effects of Input Motion on the Seismic Behaviour of Tunnels[J]. Soil Dynamics and Earthquake Engineering，2011，31(3)：452-462.

[12]朱正國,余劍濤,隋傳毅,等.高烈度活斷層地區隧道結構抗震的綜合措施[J].中國鐵道科學，2014，35(6)：55-62.

(ZHU Zhengguo, YU Jiantao, SUI Chuanyi, et al. Comprehensive Seismic Measures for Tunnel Structure in the Area of High Intensity Active Fault[J]. China Railway Science，2014，35(6)：55-62. in Chinese)

[13]趙曉勇,楊長衛,張建經.地震作用下鹽水溝隧道破壞成因研究[J].中國鐵道科學，2015，36(5)：61-67.

(ZHAO Xiaoyong, YANG Changwei, ZHANG Jianjing. Failure Mechanism of Yanshuigou Tunnel under Earthquake Action[J]. China Railway Science，2015，36(5)：61-67. in Chinese)

[14]安軍海,陶連金,李積棟,等.地鐵雙層交叉隧道非線性地震響應分析[J].中國鐵道科學，2015，36(3)：66-72.

(AN Junhai, TAO Lianjin, LI Jidong, et al. Nonlinear Seismic Response of Double-Decked Intersecting Metro Tunnel[J]. China Railway Science，2015，36(3)：66-72. in Chinese)

[15]晏啟祥,周侶,王春燕,等.用于深埋圓形盾構隧道地震效應分析的2種擬靜力解析解的對比研究[J].中國鐵道科學，2015，36(2)：45-51.

(YAN Qixiang, ZHOU Lü, WANG Chunyan, et al. Comparative Study on Two Pseudo-Static Analytical Solutions to Seismic Effect for Deep Buried Circular Shield Tunnel[J]. China Railway Science，2015，36(2)：45-51. in Chinese)

[16]胡聿賢.地震工程學[M]. 2版.北京：地震出版社，2006：16-17.

[17]THOMSEN L. Weak Elastic Anisotropy [J]. Geophysics，1986，51(10)：1954-1966.

[18]WINTERSTEIN D F. Velocity Anisotropy Terminology for Geophysicists[J]. Geophysics，1990，55(8)：1070-1088.

[19]劉晶波，杜義欣，閆秋實. 黏彈性人工邊界及地震動輸入在通用有限元軟件中的實現[J]. 防災減災工程學報，2007， 27(增刊)：37-42.

(LIU Jingbo, DU Yixin, YAN Qiushi. Realization of Viscoelastic Boundary and Seismic Input in Finite Element Software[J]. Journal of Disaster Prevention and Mitigation Engineering，2007，27(Supplement)：37-42. in Chinese)

[20]廖振鵬. 工程波動理論導論[M]. 2版. 北京：科學出版社，2002：141-155.

[21]梁鍇. TI介質地震波傳播特征與正演方法研究[D].北京：中國石油大學，2009：20-29.

(LIANG Kai.The Study on Propagation Feature and Forward Modeling of Seismic Wave in TI Media [D]. Beijing：China University of Petroleum，2009：20-29. in Chinese)

[22]吳國忱,梁鍇,戚艷平. 三維TTI介質相速度和群速度[J]. 地球物理學進展，2009，24(6)：2097-2105.

(WU Guochen, LIANG Kai, QI Yanping. Phase Velocity and Group Velocity in 3D TTI Media [J]. Progress in Geophysics，2009，24(6)：2097-2105. in Chinese)

[23]何建濤，馬懷發，張伯艷，等. 黏彈性人工邊界地震動輸入方法及實現[J]. 水利學報，2010，41(8)：960-969.

(HE Jiantao，MA Huaifa，ZHANG Boyan，et al. Method and Realization of Seismic Motion Input of Viscous-Spring Boundary[J]. Journal of Hydraulic Engineering，2010，41(8)：960-969. in Chinese)