液壓支架頂梁的重量優化

楊彥華

（山西焦煤集團有限責任公司東曲煤礦， 山西　古交　030200）

引言

特厚煤層開采對液壓支架的要求較高，工作面所選支架不僅要通過相關的強度試驗和安全性試驗，而且還需對關鍵構件進行重量優化[1-2]。在不影響支架工作性能的前提下減輕支架重量有利于支架在工作面的推移，同時還達到了節約成本和提高礦井效益的目的，大量現場實測結果表明，當支架頂梁中部受到集中載荷作用時，支架的受力情況最為糟糕。故本文再對特厚煤層采場液壓支架的頂梁進行重量優化時設定頂梁邊界約束條件為中部位置受集中應力作用，優化后的支架頂梁仍然會達到其他工況條件下的強度需求。

1　頂梁重量優化流程

頂梁重量的優化流程就是進行最優化設計，即基于最優化理論，綜合考慮多種影響因子，依附于計算機語言求得最優方案。具體流程為：根據支架工作的實際環境建立等效模型，把影響因子視為邊界約束條件，結合適合的優化方案以及計算機語言進行最優方案的求解[3-4]。本文通過Matlab進行液壓支架頂梁的重量優化，具體優化流程如圖1所示。

2　建立支架頂梁的等效模型

本文進行頂梁重量優化研究時，設定頂梁邊界約束條件為中部位置受集中應力作用。該支架為4柱支架，各個支柱的支撐力均為5.6 kN，頂梁中部位置所受的集中應力為20 kN，在工作面液壓支架受到多種載荷作用，圖2為支架所受的剪力和彎矩特征。

在圖2中，L1=0.63 m，L2=1.195 m，則根據靜力平衡條件可求得：剪力Fs1=Fs6=5×103kN，Fs2=Fs3=Fs4=Fs5=10×103kN；彎矩 M1=M7=1.23×109N·mm，M2=M6=4.38×109N·mm，M3=M5=5.61×109N·mm，M4=17.56×109N·mm。頂梁是封閉且對稱的箱體結構，如圖3所示。

圖1　液壓支架頂梁的重量優化求解示意圖

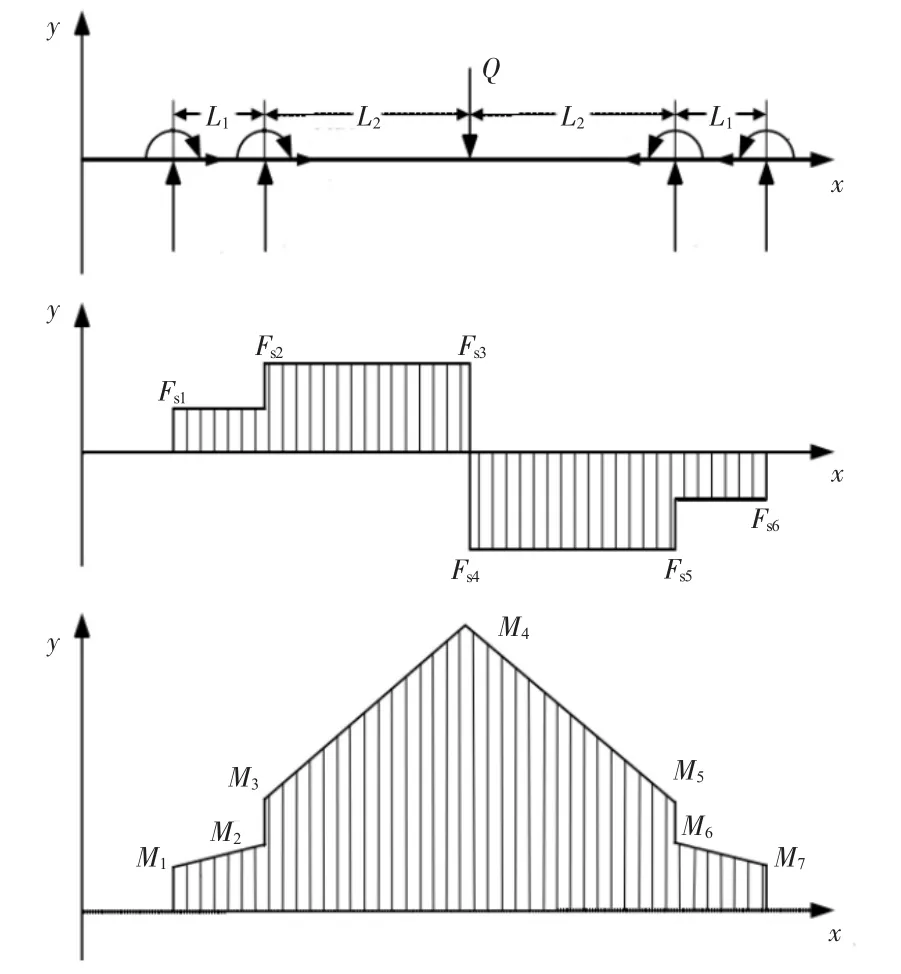
圖2　液壓支架頂梁所受的剪力和彎矩特征示意圖

圖3　液壓支架頂梁結構示意圖

根據圖3計算頂梁的彎曲正應力，計算過程如下所示。

1）頂梁結構重心到圖3的aa截面的距離yc如式（1）所示：

2）頂梁結構重心到各塊板中心處的距離ai通過式（2）計算：

3）頂梁 1～5 號板中心的慣性距 J1—J5如式（3）所示：

4）頂梁各塊板對形心的慣性距通過式（4）計算：

5）結合式（1）—（4）可求得頂梁的彎曲正應力，如式（5）所示：

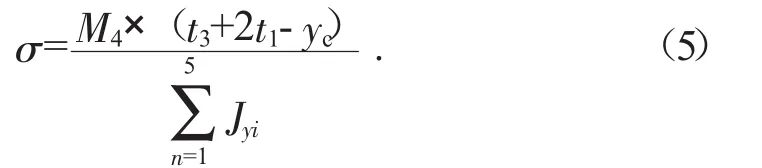
頂梁的剪應力均值通過式（6）計算：

支架頂梁的邊界受到剪應力和彎曲正應力的雙重作用，則根據式（7）可計算得到等效應力σr：

3　支架頂梁優化結果分析

將支架頂梁的邊界約束條件和目標函數轉變為Matlab可識別的形式，頂梁中部位置受集中應力作用，該位置為容易發生塑性屈服，故對該位置的強度進行校核。為了使通過Matlab計算得到的最優解可以達到各種工況條件下的需求，應力集中位置的安全系數需要設置的更大一些。頂梁的板材厚為設計變量，如式（8）所示。

本次需要進行頂梁的重量優化，故最優重量可理解為最優體積，即要求頂梁的橫截面積達到最小，故目標函數如式（9）所示。

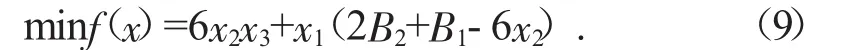
支架頂梁等效應力的最大值應該低于極限強度，同時安全系數設置為1.8，由此得到式（10）。

頂梁的上邊界條件和下邊界條件如式（11）所示。

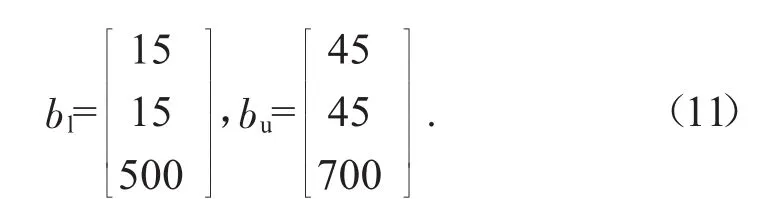
進行頂梁重量的最優化方案求解時需要注意：真實情況下支架頂梁的鋼板設計尺寸是固定的，不是連續變量，而Matlab求解的是連續變量。但求解的目標函數在最優值附近的變化十分平緩，故對Matlab求解得到的最終結果取整便得到了頂梁重量的最優值。頂梁的初始參數如表1所示，求解得到的頂梁最優參數如表2所示。

表1　支架頂梁的初始參數統計表

表2　支架頂梁的最優參數統計表

對比表1和表2可以發現，計算得到額腹板高度和厚度均與開始設置的邊界值基本相符，說明最優參數求解所得的結果受開始設置邊界值的影響較大，故在最優值求解前需要設置合理的邊界值。支架頂梁厚度由腹板的高度決定，一般情況下頂梁厚度是支架升柱高度最大值的10%，腹板高度為0.68 m，而其長度為6.8 m，腹板處于頂梁的縱向位置，為了保證腹板在受載作用下依然保持較高的剛度，故腹板厚度設計為15 mm，這就得到了表2中頂梁的最優參數。將表2中頂梁的最優參數進行標準化處理，由此得到的最優標準參數如下頁表3所示。

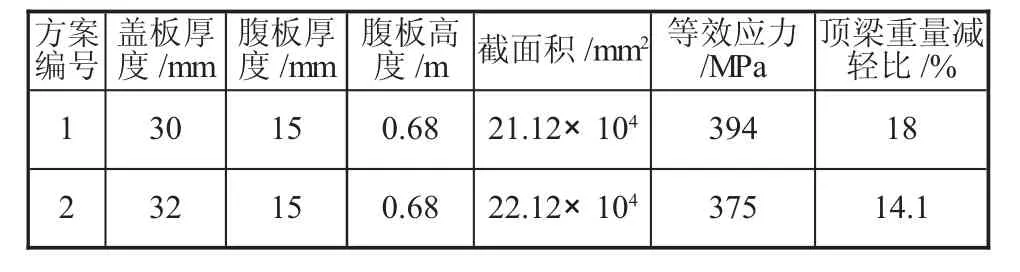
表3　支架頂梁的最優標準參數統計表

對表3中的兩個方案進行比較可以發現，方案一頂梁重量減輕了18%，要優于方案二，但方案一下頂梁的截面積要小于方案二；頂梁所用材料的極限強度為380 MPa，屈服強度為700 MPa，而方案一下等效應力為394 MPa，處于極限強度和屈服強度之間，方案二等效應力為375 MPa，處于極限強度以下，從礦井安全開采的角度分析，方案二要更優一些。

4　支架頂梁變量的敏感性分析

在支架頂梁的各項參數中，重量最優值受腹板的高度和厚度以及蓋板厚度的影響，但各因素的影響程度不同，故需要對這三個影響因素的影響效果（敏感性）進行定量評價，頂梁等效應力最大值與這三個因素間的關系如圖4所示。

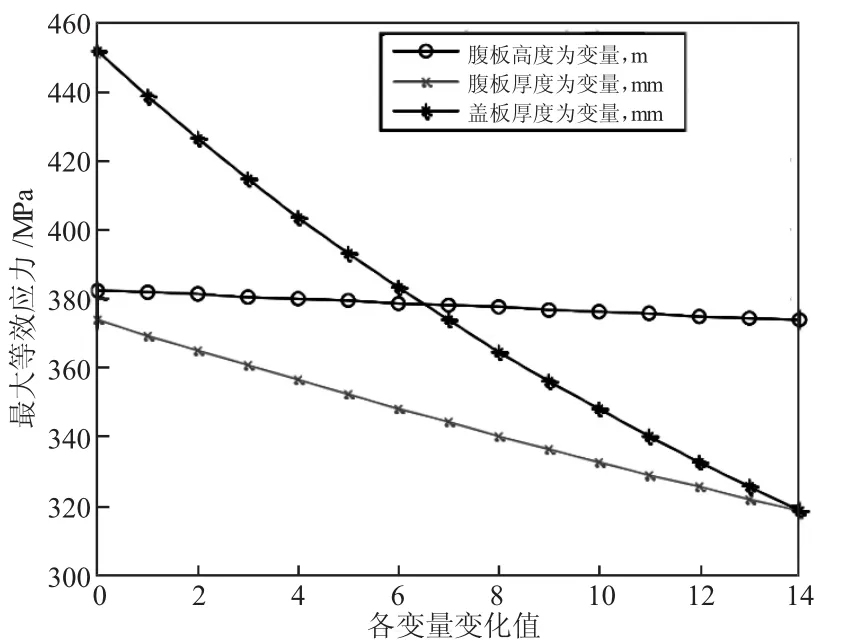
圖4　頂梁等效應力最大值與各個因素間的關系示意圖

從圖4中可以看出，頂梁等效應力最大值與各因素均呈現為負相關關系，但隨著橫坐標的增大，等效應力最大值的減小速率不同，按從高到低的順序可排為：蓋板厚度>腹板厚度>腹板高度，由此說明對頂梁等效應力的影響效果可排為：蓋板厚度>腹板厚度>腹板高度。頂梁截面積與這三個因素間的關系如圖5所示。

從圖5中可以看出，頂梁截面積與各因素均呈現為正相關關系，但隨著橫坐標的增大，等截面積增大的速率不同，按從高到低的順序可排為：蓋板厚度>腹板厚度>腹板高度，由此說明對頂梁截面積的影響效果可排為：蓋板厚度>腹板厚度>腹板高度。

綜合而言，蓋板厚度與初始值較為相符，究其原因，蓋板厚度對頂梁截面積的影響效果最為顯著，但當蓋板厚度過小時，則頂梁的等效應力過大，很容易導致材料發生塑性屈服。腹板厚度對頂梁截面積和等效應力的影響效果也較為明顯，故對支架頂梁進行重量優化時主要可以通過減小腹板厚度的手段來實現，通過對比表1—表3也發現腹板厚度減小的程度最大。腹板高度對頂梁截面積和等效應力的影響效果不是十分明顯，故可以通過以減小腹板高度為輔的手段來進行頂梁重量優化。

圖5　頂梁截面積與各個因素間的關系示意圖

5　結論

在不影響支架工作性能的前提下減輕支架重量利于支架在工作面的推移，同時還達到了節約成本和提高礦井效益的目的。本文對特厚煤層采場液壓支架的頂梁進行重量優化。主要結論如下：

1）從頂梁重量減輕最大以及保證礦井安全生產的角度聯合分析，可得到優化蓋板厚度為32 mm、腹板厚度15 mm、腹板高度0.68 m，在該條件下頂梁重量減輕了14.1%。

2）對支架頂梁變量的敏感性進行了分析，認為對頂梁重量最優解的影響程度可排為蓋板厚度>腹板厚度>腹板高度。綜合分析認為對支架頂梁進行重量優化時應該采取以減小腹板厚度為主和以減小腹板高度為輔的手段，而本文得到的支架頂梁最優參數也證明了該結論的正確性。

[1]李亞飛，李炳文，張席.基于遺傳算法的超靜定液壓支架頂梁優化設計[J].煤礦機械，2015（4）：11-13.

[2]朱強，秦東晨，姚向豫.基于ANSYS的液壓支架掩護梁結構優化研究[J].煤礦機械，2012（4）：2-4.

[3]李秋生，王勇，教光印，等.基于VC++液壓支架四連桿機構的優化設計與分析[J].煤礦機械，2010（11）：23-24.

[4]葉鐵麗，李民，劉欣麗.基于COSMOSWorks的液壓支架頂梁優化設計[J].煤炭工程，2009（12）：111-113.