考慮布儒斯特角約束的超低空機(jī)動目標(biāo)攔截

陳 峰,何廣軍,何陽光,熊思宇

(空軍工程大學(xué) 防空反導(dǎo)學(xué)院,陜西 西安 710051)

在目標(biāo)處于低空、超低空飛行情況下,由于受到地海雜波及多徑效應(yīng)的影響,雷達(dá)導(dǎo)引頭在跟蹤探測目標(biāo)時性能大大下降[1]。提高防空導(dǎo)彈的超低空攔截性能一直是防空領(lǐng)域的一個難題。對超低空攔截精度影響最大的是多徑效應(yīng),這種效應(yīng)會導(dǎo)致雷達(dá)導(dǎo)引頭無法有效跟蹤辨識真實目標(biāo)與鏡像虛假目標(biāo),造成角跟蹤誤差,引起脫靶[1-2]。目前,國內(nèi)外大量研究表明,對抗多徑,抑制雜波的根本途徑是變被動處理為主動抑制。其主要有2個技術(shù)突破口:一是寬帶探測信號,尋找最佳的信號帶寬,使導(dǎo)引頭的信雜比最優(yōu)[3];二是設(shè)計布儒斯特彈道,尋找一個最佳的彈目視線角,也就是布儒斯特角,來有效避免多徑效應(yīng)[4],使導(dǎo)引頭受到的多徑干擾最小,從而準(zhǔn)確跟蹤攔截超低空目標(biāo)。文獻(xiàn)[5-7]對末端攻擊角度進(jìn)行了深入研究,但是其只能在攻擊末端時刻將落角約束至期望的角度,而超低空攔截為了降低多徑干擾的影響,需將彈目視線角盡快約束至布儒斯特角附近。

本文在文獻(xiàn)[8-10]滑模變結(jié)構(gòu)制導(dǎo)律思想的基礎(chǔ)上,設(shè)計出一種自適應(yīng)變結(jié)構(gòu)末制導(dǎo)律,通過調(diào)整變結(jié)構(gòu)參數(shù),加快彈目視線角收斂至布儒斯特角的速率,同時將角速率收斂至0,使多徑干擾降到最小。針對超低空目標(biāo)機(jī)動加速度難以準(zhǔn)確測量和估計的問題,采用小角度線性化的方法對所設(shè)計的制導(dǎo)律進(jìn)行改進(jìn),結(jié)果表明,改進(jìn)后的制導(dǎo)律仍具有理想的超低空攔截性能,且其數(shù)學(xué)形式簡單,在工程實踐上更具有可行性。

1 布儒斯特效應(yīng)與超低空攔截

1.1 布儒斯特效應(yīng)

布儒斯特效應(yīng)在電磁學(xué)中定義為垂直極化波鏡面反射系數(shù)最小時的入射角;而在防空導(dǎo)彈雷達(dá)導(dǎo)引頭中定義為雷達(dá)導(dǎo)引頭超低空下視探測環(huán)境時,多徑干擾強(qiáng)度最小的波束照射角。

多徑干擾來源于地面、海面與低空目標(biāo)間的電磁耦合作用,因受到目標(biāo)與地面、海面的雙重調(diào)制,而具有類目標(biāo)特性,如圖1所示。

圖1 多徑干擾示意圖

防空導(dǎo)彈雷達(dá)導(dǎo)引頭下視探測超低空目標(biāo)時,目標(biāo)越低,與地面或海面的耦合越強(qiáng),多徑干擾也越強(qiáng)。多徑的存在會導(dǎo)致雷達(dá)導(dǎo)引頭無法有效辨識真實目標(biāo)與鏡像虛假目標(biāo),造成跟蹤錯誤,或跟蹤真實目標(biāo)與鏡像目標(biāo)的合成相位中心,造成角跟蹤誤差,引起脫靶。因此,研究超低空攔截問題必須從避免多徑干擾方面突破。防空導(dǎo)彈在攔截超低空目標(biāo)時,根據(jù)地面、海面環(huán)境反射系數(shù)隨角度的變化規(guī)律,存在一個環(huán)境反射最小的角度,稱為布儒斯特角,如果導(dǎo)彈按布儒斯特角探測攔截目標(biāo),可有效降低多徑干擾的影響。同時,不同環(huán)境的布儒斯特角也是不同的,海洋環(huán)境在10°左右,沙漠環(huán)境在30°左右[3]。

1.2 超低空攔截模型

圖2 超低空攔截模型

導(dǎo)彈與目標(biāo)相對運動方程:

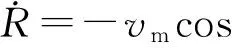
(1)

(2)

(3)

(4)

2 自適應(yīng)變結(jié)構(gòu)制導(dǎo)律

2.1 自適應(yīng)變結(jié)構(gòu)制導(dǎo)律設(shè)計

在目標(biāo)超低空飛行情況下,導(dǎo)彈在終端攻擊目標(biāo)時,視線角需穩(wěn)定在期望的布儒斯特角附近,同時也要滿足視線角速率收斂至0,降低脫靶量的要求。即

(5)

式中:qd(tf)為期望的視線角,tf代表攔截彈擊中目標(biāo)的時刻。

因此可選取雙滑模面:

S1=x1=q(t)-qd(tf)

(6)

(7)

根據(jù)所取狀態(tài)變量和導(dǎo)彈攔截目標(biāo)的相對運動方程,可得狀態(tài)方程:

(8)

S=x2+λvmx1/R

(9)

式中:系數(shù)λ為正的常數(shù),當(dāng)S=0時,系統(tǒng)的狀態(tài)是沿滑模面運動。此時,系統(tǒng)狀態(tài)的轉(zhuǎn)移不再受系統(tǒng)中參數(shù)變化和外部擾動的影響,具有較強(qiáng)的魯棒性;當(dāng)x1=x2=0時,導(dǎo)彈可以按照所設(shè)計的期望布儒斯特角探測攔截目標(biāo)。

為保證系統(tǒng)狀態(tài)能到達(dá)滑模面且在趨近滑模面運動的過程中有良好的動態(tài)特性,同時由于式(8)所示的系統(tǒng)為時變系統(tǒng),因此可構(gòu)造對時變參數(shù)具有自適應(yīng)能力的趨近律,即

(10)

式中:ε,k均為大于0的常數(shù)。

(11)

對式(9)求導(dǎo),并聯(lián)立式(6)和式(7),可得:

(12)

由式(1)～式(4),聯(lián)立式(11)和式(12),求得自適應(yīng)變結(jié)構(gòu)制導(dǎo)律:

(13)

現(xiàn)實中,由于滑模變結(jié)構(gòu)控制存在不連續(xù)開關(guān)項,會使得滑動模態(tài)出現(xiàn)抖振現(xiàn)象。故采用高增益連續(xù)函數(shù)Θ(S)=S/(|S|+δ)代替符號函數(shù)sgnS,以消除抖振的影響,其中δ是很小的正常數(shù),代表著所設(shè)計的連續(xù)化函數(shù)接近sgnS的程度[11]。

這樣經(jīng)過光滑處理的滑模制導(dǎo)律為

(14)

2.2 仿真驗證

1)仿真1:制導(dǎo)律有效性的驗證。

在沙漠環(huán)境下,分別對不同機(jī)動的超低空目標(biāo)進(jìn)行迎面攔截仿真驗證。

設(shè)目標(biāo)1進(jìn)行正弦爬升機(jī)動,假設(shè)其機(jī)動加速度可獲得,設(shè)為at1=-40sin(0.5πt),目標(biāo)2進(jìn)行一種S形軌跡機(jī)動,這種機(jī)動更為復(fù)雜,其加速度為

設(shè)超低空目標(biāo)1和目標(biāo)2的初始飛行高度分別為Y1=Y2=30 m,初始位置分別為X1=X2=6 000 m,初始速度分別為vt1=vt2=400 m/s,機(jī)動加速度分別為at1和at2,初始彈道傾角分別為θt1=θt2=180°;攔截彈的初始水平位置Xm=0 m,高度Ym=3 000 m,初始速度vm=580 m/s,初始彈道傾角θm=-30°。參數(shù)設(shè)置為λ=10,k=2,ε=100,δ=0.01。由前面已知,沙漠環(huán)境的布儒斯特角在30°左右(這里只是表示角度的大小,按照圖2標(biāo)注的方向應(yīng)為負(fù)值)。仿真結(jié)果見圖3～圖7。

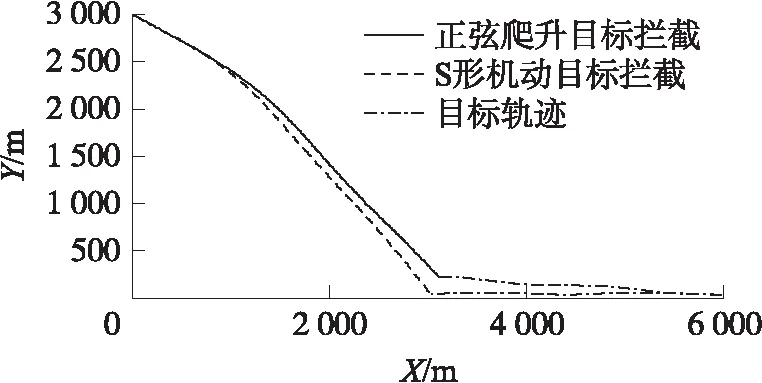
圖3 攔截機(jī)動目標(biāo)的布儒斯特彈道

圖4 視線角響應(yīng)曲線

圖5 視線角速率響應(yīng)曲線

圖6 目標(biāo)加速度變化曲線

圖7 攔截彈加速度響應(yīng)

對于攔截沙漠上的超低空目標(biāo),由于其布儒斯特角在30°左右,為了降低多徑干擾對導(dǎo)引頭制導(dǎo)精度的影響,需將視線角盡快控制至30°。超低空來襲目標(biāo)進(jìn)行突防時,可能會采取不同的機(jī)動加速度。由圖3可以看出,改變超低空目標(biāo)的機(jī)動突防方式,攔截彈最終總可以以較平直的布儒斯特彈道擊中目標(biāo)。根據(jù)圖4和圖5,針對不同的機(jī)動目標(biāo),該制導(dǎo)律最終總可以將視線角大小控制至30°,即沙漠環(huán)境的布儒斯特角,且視線角速率收斂至0,保證了攔截彈最終以期望的布儒斯特角攻擊目標(biāo),從而降低了多徑干擾的影響,提高了制導(dǎo)的精度。且由圖6、圖7可知,當(dāng)目標(biāo)以4g(g為重力加速度)的加速度做機(jī)動突防時,攔截彈為了將視線角快速地約束至布儒斯特角附近,導(dǎo)致攔截彈在1～3 s時間段里的加速度響應(yīng)達(dá)到了11g,這也說明了反導(dǎo)比突防的要求更高,難度也更大,符合實際工程情況;但在3 s以后的時間段內(nèi),攔截彈加速度幅值迅速降到4g,和突防目標(biāo)一致大小,驗證了所設(shè)計制導(dǎo)律的有效性與魯棒性。

2)仿真2:制導(dǎo)律參數(shù)ε的選取。

下面著重討論式(14)中制導(dǎo)律參數(shù)ε值的選取原則,對正弦爬升機(jī)動目標(biāo)進(jìn)行攔截仿真驗證。仿真初始條件的設(shè)置參照仿真1,這里只是改變參數(shù)ε值的大小。仿真結(jié)果如圖8～圖10所示。

由圖8和圖9可以看出,增大ε值,可以加快視線角的收斂速度,使視線角更快地約束至期望的布儒斯特角附近。但是,當(dāng)ε=100時,再繼續(xù)增大ε值,視線角的收斂速度基本保持不變,此時如圖10所示,攔截彈的起始過載會迅速增大,這對攔截彈的性能要求很高。因此,ε=100為最佳取值,既能使視線角快速約束至布儒斯特角,同時又能保證攔截彈的起始過載只有2g。

圖8 不同ε時的視線角

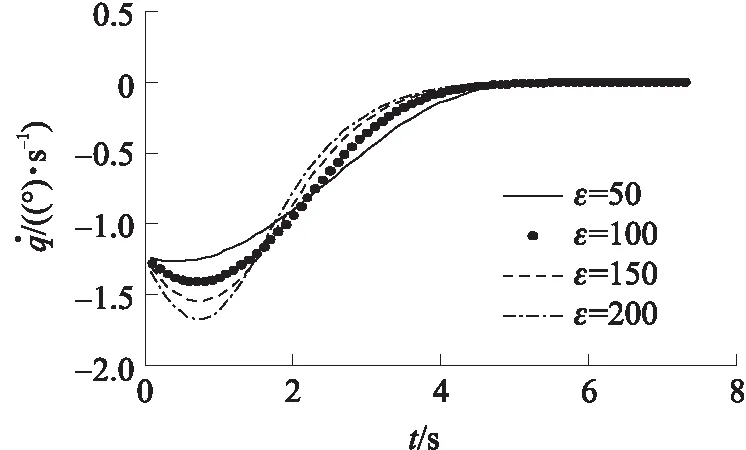
圖9 不同ε時的視線角速率

圖10 不同ε時的攔截彈加速度指令

參數(shù)k的選取原則可參照ε的選取原則,需折中考慮視線角的收斂速度和攔截彈的過載限制。

3 改進(jìn)的制導(dǎo)律

在實際的攔截過程中,機(jī)動目標(biāo)的加速度是無法準(zhǔn)確獲得的,需要對其進(jìn)行估計。目前對目標(biāo)加速度的估計大多是從濾波算法和狀態(tài)觀測器方面研究[12-13],但是這些都需要先建立相應(yīng)的模型,有些濾波算法甚至還要求噪聲是特定類型的。而超低空攔截時,多徑散射信號的形成及目標(biāo)-環(huán)境的復(fù)合散射模型是極其復(fù)雜的,相應(yīng)的多徑干擾及雜波影響也是極其復(fù)雜的。若用以上方法對目標(biāo)加速度進(jìn)行估計,會使得目標(biāo)的加速度估計還是不準(zhǔn)確。如果將不準(zhǔn)確的目標(biāo)加速度估計信息反饋到制導(dǎo)指令中,則會大大降低超低空目標(biāo)的攔截精度,甚至可能導(dǎo)致脫靶。因此,本文在所設(shè)計的制導(dǎo)律的基礎(chǔ)上以一種小角度線性化的方法對其進(jìn)行改進(jìn)。

sinq1=Y1/R

(15)

式中:R為彈目相對距離,由于q1是個無窮小量,則式(15)可簡化為

q1=Y1/R

(16)

對式(16)求一階導(dǎo)數(shù),可得:

(17)

式(17)可改寫成:

(18)

對式(17)求導(dǎo),并聯(lián)立式(18),最終得到:

(19)

(20)

將式(20)代入式(19),得到:

(21)

切換函數(shù)取式(9),趨近律取式(10),依照求式(13)的方法,得到此時的制導(dǎo)指令:

(22)

將目標(biāo)在超低空環(huán)境中的小機(jī)動加速度視為干擾項予以忽略,式(22)可寫為

(23)

(24)

同樣,為了消除抖振的影響,仿照式(14),得到最終的制導(dǎo)指令:

(25)

對比式(14)和式(25),可以看出,通過小角度線性化改進(jìn)后的制導(dǎo)律與原變結(jié)構(gòu)制導(dǎo)律相比,方程更加簡單,變量的個數(shù)也大大減小了。無需準(zhǔn)確知道目標(biāo)的機(jī)動加速度,無須測量攔截彈的彈道傾角,無需計算三角函數(shù),大大減少了測量計算中出現(xiàn)的各種誤差。且無需準(zhǔn)確知道超低空目標(biāo)的機(jī)動加速度,有效避免了多徑效應(yīng)和雜波對目標(biāo)機(jī)動加速度估計的影響,更易于工程實現(xiàn)。

4 算例分析

為了驗證改進(jìn)后制導(dǎo)律的有效性,將其與第2節(jié)中的自適應(yīng)變結(jié)構(gòu)制導(dǎo)律進(jìn)行比較。

設(shè)超低空目標(biāo)的初始飛行高度Yt=10 m,初始位置Xt=6 000 m,初始速度vt=400 m/s,目標(biāo)做正弦爬升機(jī)動,加速度at=-40sin(0.5πt),初始彈道傾角θt=180°;攔截彈的初始位置Xm=0 m,高度Ym=3 000 m,初始速度vm=580 m/s,初始彈道傾角θm=-30°。參數(shù)設(shè)置為λ=10,k=2,ε=100,δ=0.01,由前面已知,沙漠環(huán)境的布儒斯特角在30°左右。仿真結(jié)果如圖11～圖14所示。

圖11 攔截彈道對比

圖12 視線角變化對比

圖13 視線角速率變化對比

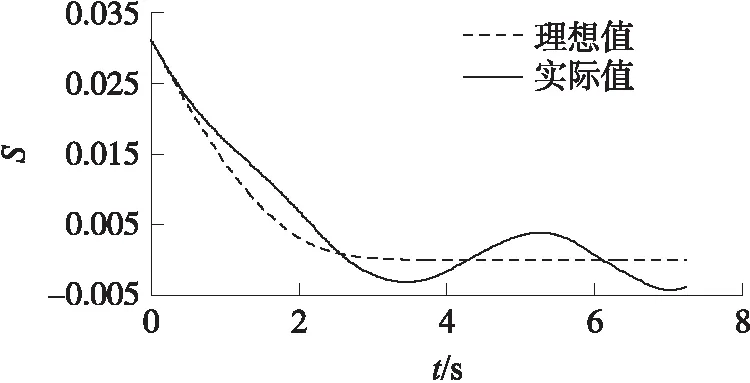
圖14 滑模面曲線對比

圖11中,理想攔截彈道是根據(jù)式(14)所設(shè)計的理想制導(dǎo)律得到的,其前提是假定超低空目標(biāo)的機(jī)動加速度已知。因此圖12～圖14中相應(yīng)的視線角變化曲線、視線角速率變化曲線和滑模面變化曲線光滑平直。而在實際的超低空攔截中,由于受到多徑效應(yīng)及地、海雜波的影響,目標(biāo)的機(jī)動加速度是無法準(zhǔn)確測量或估計出來的。采用小角度線性化的方法對理想的制導(dǎo)律進(jìn)行改進(jìn),使其更符合工程實際。因此,圖12～圖14中相應(yīng)的實際視線角變化曲線、視線角速率變化曲線和滑模面變化曲線會在理想值的附近出現(xiàn)一定微小范圍的波動。但從圖11、圖12可看出,通過式(25)改進(jìn)后制導(dǎo)律得到的實際攔截彈道并不影響超低空目標(biāo)的攔截性能,仍能以近似理想的布儒斯特彈道擊中目標(biāo)。

5 結(jié)論

針對雷達(dá)導(dǎo)引頭下視探測超低空目標(biāo)時環(huán)境多徑效應(yīng)影響導(dǎo)致的跟蹤精度下降的問題,設(shè)計出一種自適應(yīng)變結(jié)構(gòu)末制導(dǎo)律。該制導(dǎo)律可確保雷達(dá)導(dǎo)引頭在探測跟蹤超低空目標(biāo)的過程中,將彈目視線角收斂至期望的布儒斯特角附近,從而降低多徑干擾的影響。考慮實際工程應(yīng)用中目標(biāo)機(jī)動加速度無法準(zhǔn)確獲得的問題,采用小角度線性化的方法對理想條件下的制導(dǎo)律進(jìn)行改進(jìn)。結(jié)果表明,改進(jìn)后的制導(dǎo)律無須事先知道目標(biāo)的機(jī)動加速度,且其數(shù)學(xué)形式簡單,在工程實踐上更具有可行性。

[1] 束川良. 適用于通用布儒斯特角的防空導(dǎo)彈超低空彈道設(shè)計[J]. 地面防空武器,2008,39(3):23-26.

SHU Chuanliang. Super low altitude air defense missile trajectory suitable for general Brewster angle[J]. Land-based Air Defence Weapons,2008,39(3):23-26. (in Chinese)

[2] 王利軍,郭建明,郝晶. 多徑效應(yīng)對雷達(dá)探測低空巡航導(dǎo)彈的影響[J]. 雷達(dá)科學(xué)與技術(shù),2010,8(1):7-11.

WANG Lijun,GUO Jianming,HAO Jing. The influence of multi-path effect on low altitude cruise missile detection in radar[J]. Radar Science and Technology,2010,8(1):7-11. (in Chinese)

[3] 隋棟訓(xùn),童創(chuàng)明,彭鵬. 超低空目標(biāo)的廣義布儒斯特效應(yīng)[J]. 空軍工程大學(xué)學(xué)報,2015,16(4):29-32.

SUI Dongxun,TONG Chuangming,PENG Peng. A study of G-Brewster of super-low altitude target[J]. Journal of Air Force Engineering University,2015,16(4):29-32. (in Chinese)

[4] 王國勝,李蕓. 一種滿足布魯斯特角約束的導(dǎo)引律研究[J]. 現(xiàn)代防御技術(shù),2014,42(3):70-74.

WANG Guosheng,LI Yun. Guidance law for restraint of Brewster angle[J]. Modern Deffence Technology,2014,42(3):70-74. (in Chinese)

[5] 李強(qiáng),盧寶剛,王曉輝. 一種導(dǎo)彈終端侵徹多約束最優(yōu)制導(dǎo)方法[J]. 兵工學(xué)報,2016,37(6):1 132-1 137.

LI Qiang,LU Baogang,WANG Xiaohui. A terminal multi-constraint optimal guidance law for missile[J]. Acta Armamentarii,2016,37(6):1 132-1 137. (in Chinese)

[6] 張寬橋,楊鎖昌,陳鵬. 帶落角約束的自適應(yīng)滑模變結(jié)構(gòu)導(dǎo)引律[J]. 現(xiàn)代防御技術(shù),2016,44(3):44-51.

ZHANG Kuanqiao,YANG Suochang,CHEN Peng. Adaptive sliding mode variable structure guidance law with impact angle constraint[J]. Modern Deffence Technology,2016,44(3):44-51. (in Chinese)

[7] ZHAO Y,SHENG Y Z. Sliding mode control based guidance law with impact angle constraint[J]. Chinese Journal of Aeronautics,2014,27(1):145-152.

[8] HE S M,LIN D F. Sliding mode based impact angle guidance law considering actuator fault[J]. Optik,2015,126(20):2 318-2 323.

[9] WANG H Q,CAO D Q,WANG X D. The stochastic sliding mode variable structure guidance laws based on optimal control theory[J]. Journal of Control Theory and Applications,2013,11(1):86-91.

[10] HAN Y H,XU B. Variable structure guidance law for attacking surface maneuver targets[J]. Journal of Systems Engineering and Electronics,2008,19(2):337-341.

[11] 辛騰達(dá),范惠林,閆琳. 滑模變結(jié)構(gòu)制導(dǎo)律的抖振問題研究[J]. 航空兵器,2015(2):10-13.

XIN Tengda,FAN Huilin,YAN Lin. Study on chattering of sliding mode variable structure guidance law[J]. Aero Weaponry,2015(2):10-13. (in Chinese)

[12] 曹有亮,張金鵬. 擴(kuò)展卡爾曼濾波器的目標(biāo)機(jī)動信息估計研究[J]. 航空兵器,2016(1):40-44.

CAO Youliang,ZHANG Jinpeng. Researeh on target maneuvering information estimation method of EKF[J]. Aero Weaponry,2016(1):40-44. (in Chinese)

[13] 王華吉,簡金蕾,雷虎民. 帶擴(kuò)張觀測器的新型滑模導(dǎo)引律[J]. 固體火箭技術(shù),2015,38(5):622-627.

WANG Huaji,JIAN Jinlei,LEI Humin. A new sliding mode guidance law based on extended state observer[J]. Journal of Solid Rocket Technology,2015,38(5):622-627. (in Chinese)