機械工程設計中的近似NURBS曲面蒙皮技術

劉 馥 于文強

曲面造型是機械工程設計的重要內容，通過構建滿足用戶所需形狀、光滑性等約束條件的曲面，進而生成三維模型。在各種各樣的曲面造型技術中，曲面蒙皮是最重要的技術之一。其主要步驟是在空間布置若干條截面線，然后用一張曲面去插值這些曲線，使得這些曲線在最終的曲面上是等參線。在機械設計領域，通常用B樣條或NURBS表示曲面[1]。由于B樣條和NURBS曲面蒙皮的重要性，很多學者對此展開研究。姚運萍等人利用B樣條曲面蒙皮技術擬合三維空間的葉片測量點列，實現葉片曲面的重構[2]。賈明等人提出了基于矩形拓撲區域的曲面局部協調設計方法，可對跨多張曲面的局部矩形拓撲裁剪區域進行重建[3]。

對于B樣條和NURBS曲面蒙皮而言，除了滿足形狀和連續性約束外，蒙皮過程中會產生大量的控制點，嚴重影響后續曲面的處理效率。為此，王文珂等人提出一種誤差可控的B樣條曲面蒙皮方法，可在誤差范圍內有效減少蒙皮曲面的控制點數目[4]。隨后，李濤等人提出了兩組相交截面線的雙向蒙皮方法[5]。但是，這兩種方法都是針對B樣條曲面的，不能處理NURBS曲面蒙皮問題。眾所周知，B樣條是NURBS的特例，即NURBS控制點權值都為1時的退化情況。相比B樣條曲面，NURBS曲面可以表示更多的形狀，形狀控制也更加靈活。此外，王文珂等人提出的方法并沒有充分利用用戶給定誤差。對于少數曲線來說，原始曲線和刪除節點后的曲線間的距離較為接近用戶給定誤差；但是對于大多數其他曲線來說，兩者的距離要比給定誤差小得多。本文將王文珂等人提出的方法推廣應用到NURBS曲面蒙皮的情況，同時利用“殘留”誤差，可以在誤差范圍內進一步減少蒙皮曲面的控制點。

1 NURBS曲面近似蒙皮算法

為了推導方便，首先考慮B樣條曲面近似蒙皮問題。給定一組相容的B樣條曲線，通過插值各曲線對應的控制點即可得到蒙皮面的控制點。為了后續敘述方便，本文把蒙皮過程叫做v方向插值。本文首先利用王文珂等人提出的方法得到一組相容的且滿足誤差要求的B樣條曲線。由于很多曲線仍存在殘留物差，因此人們并不需要精確插值這些曲線，這也給人進一步減少蒙皮面控制點的空間。在本文算法中，首先插值v方向的曲線，然后在誤差范圍內進一步減少蒙皮曲面控制點。

首先估計第t條截面線和刪除節點后的曲面間距離，令：

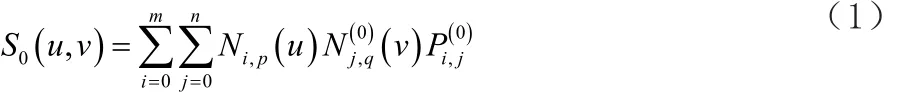
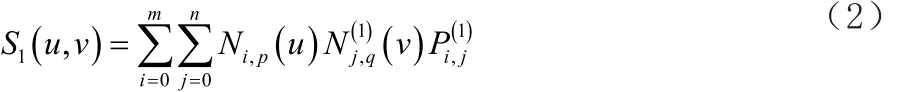
它們分別表示原始曲面和刪除第s個節點后的曲面。第t條曲線在S0(u,v)上是等參線。用vt表示它在曲面S0(u,v)上v向的參數值。對應的，曲面S1(u,v)上也有一條等參線S1(u,vt)。曲線S0(u,vt)和曲面S1(u,v)之間的距離不會大于兩條等參線間的距離。

用r表示被刪除節點的重數，令：

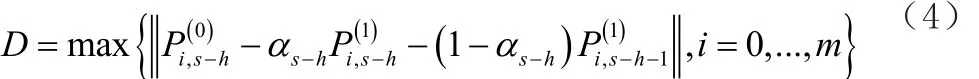
根據節點刪除公式，同時令：

現在考慮NURBS的情況，將NURBS曲面寫成齊次坐標的形式，可以類似地得到如下估計式：

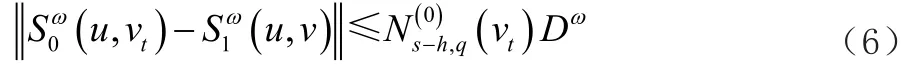
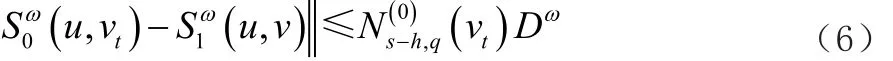
可以得到曲線S0(u,vt)和曲面S1(u,v)間的距離估計式：

其中

上述距離估計式是在齊次坐標下推算出的，不能直接用于計算三維空間中曲線曲面間的距離。利用齊次坐標和三維坐標的關系，可得NURBS曲線和曲面在三維空間的距離估計式：

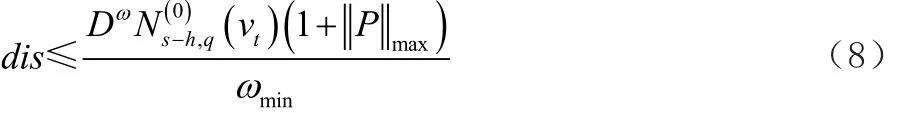
如果曲面遠離坐標原點，則||Pmax||會很大。因此，人們對曲面做平移來減小||Pmax||。用Pc表示曲面重心，于是式（3）變為：

式（1）和（4）分別給出了B樣條曲線曲面間距離和NURBS曲線曲面間距離的估計式。如果人們需要刪除多個節點，則只需要單獨刪除每個節點，然后用式（1）和式（4）估計距離，將所有距離相加即可得曲線曲面間距離的一個上屆估計。

基于上述推導，本文算法的主要思想是依次刪除使得曲線曲面間距離最小的節點。首先，對于每個待刪除節點，估計刪除該節點后各曲線和曲面間的距離，距離最大的定義為刪除該節點后的刪除誤差；然后將刪除誤差最小的節點刪除；此過程一直進行，直到所有節點都被刪除或最小的刪除誤差也大于用戶給定誤差。

2 實驗結果

為了驗證本文方法的有效性，下面用汽車設計中的兩個曲面蒙皮例子進行測試。圖1是車頭曲面的蒙皮結果，其中圖1的上部曲面是用傳統蒙皮方法得到的曲面，共含有160個控制點。設定誤差為1mm，則利用本文方法得到的曲面只含有16個控制點，如圖1下部所示，相當于原有方法的10%。由于給定誤差很小，本文方法得到的曲面和精確的曲面非常接近，這使得人們很難表示兩曲面間的距離。為了顯示方便，圖1右部給出了兩曲面上兩條等參線（u=0.75），通過放大人們可以看到兩曲線間的距離。

第二個例子是車頭及車窗曲面的蒙皮結果。圖2上部顯示為綠色的三個曲面共含有2430個控制點。同樣設定誤差為1mm，利用本文方法得到的三個曲面共含有220個控制點，只相當于傳統方法的9.05%。

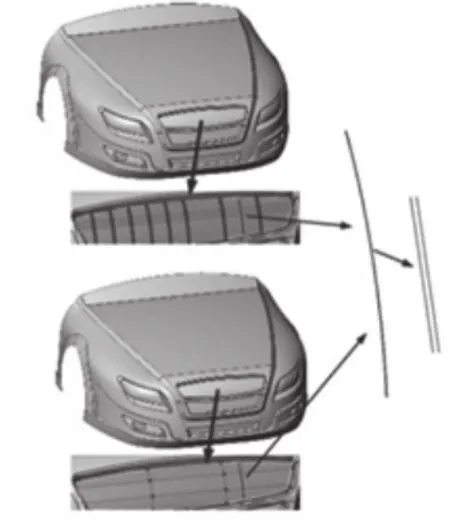
圖1 車頭曲面蒙皮結果

圖2 車頭及車窗曲面蒙皮結果

3 結語

本文提出了一種機械工程設計中的近似NURBS曲面蒙皮方法。本方法首先給出了輸入曲線和減少控制點后的曲面間距離的誤差估計，然后基于該估計式，利用冗余誤差來減少NURBS曲面蒙皮過程中的控制點。實驗結果證明了本文方法的有效性。

[1]施法中.計算機輔助幾何涉及與非均勻有理B樣條[M].北京：高等教育出版社，2001：212-214.

[2]姚運萍，盛晟，王薇.葉片蒙皮曲面重構方法的研究[J].機械制造，2013，51（582）：24-26.

[3]賈明，呂震，李永青，等.基于B樣條曲面裁剪計算的局部協調設計[J].機械工程學報，2003，39（2）：74-78.

[4]王文珂，張慧，王斌.誤差可控的近似B樣條曲面蒙皮算法[J].計算機輔助設計與圖形學學報，2008，20（11）：1477-1482.

[5]李濤，劉浩.B樣條曲面的雙向插值造型算法[J].計算機工程與應用，2012，48（35）：178-181.