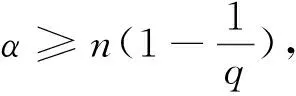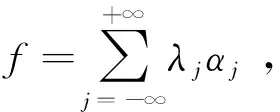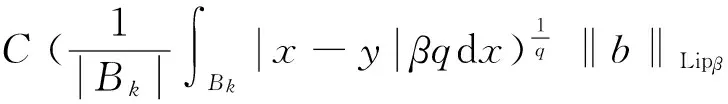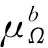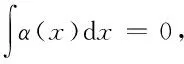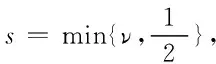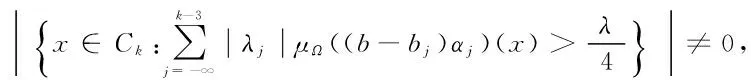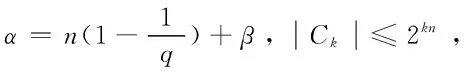變量核Marcinkiewicz積分交換子在弱Herz空間上的有界性
邵旭馗,王素萍
(隴東學院 數學與統計學院,甘肅 慶陽 745000)
記Sn-1為Rn(n≥2)中的單位球面,其上裝備了Lebesgue 測度dσ=dσ(z′).設定義在Rn×Rn上的函數Ω(x,z)∈L∞(Rn)×Lr(Sn-1)(r≥1), 滿足
(1)
其中
?z∈Rn{0}.
設Ω滿足條件
Ω(x,λz)=Ω(x,z),?x,z∈Rn,?λ>0,
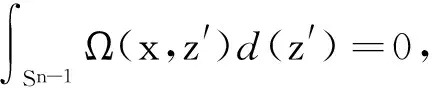
(2)
稱函數f(x)∈Lipν(Rn),如果滿足
(3)
定義Marcinkiewicz積分μΩ如下
(4)
Stein[1]首次定義了Marcinkiewicz積分μΩ,得到當Ω∈Lip(Rn)時μΩ的(p,p)有界性;Torchinsky等[2]又證明了μΩ與函數b∈BMO(Rn)的交換子μΩ,b加權有界性.其中
(5)
王婭昕[3]研究了b∈Lipβ(Rn)時交換子μΩ,b的有界性;Mo等[4]進一步考慮了多線性的情形.
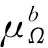
(6)
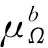
先給出一些定義與記號:設k∈Z, 令Bk=B(0,2k)={x∈Rn:|x|≤2k},Ck=BkBk-1,并記χk=χCk為集Ck的特征函數.
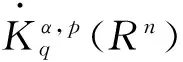
(7)
其中
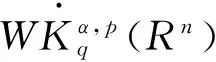
(8)
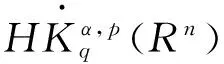
(9)
其中:S′(Rn)表示Rn上的緩增廣義函數空間,G(f)是f的Grand極大函數.
定義4[15]設α∈R,1 suppα?B(0,r)={x∈Rn:|x|≤r}, 定理1設Ω(x,y)∈L∞(Rn)×Lipν(Sn-1)滿足(2)式,α∈R,b∈Lipβ(Rn),其中 并且有 其中:上式中下確界是在f的所有分解上取得. 引理2設 如果Ω(x,y)∈L∞(Rn)×Lipν(Sn-1),b∈Lipβ(Rn),有 引理2的證明參見文[3]. 引理3設b∈Lipβ(Rn),0≤β<1,有 其中 證明 ≤ 當0 當p>1時,由α∈R,有 因此 以下估計I1,因為 所以,有 由x∈Ck,有 由于x∈Ck,y∈Bj,且j≤k-3,故|x-y|~|x|~|x|+2j+1.由H?lder不等式、Minkowski不等式及αj的性質,有 對x∈Ck,y∈Bj,且j≤k-3,Ω(x,y)∈L∞(Rn)×Lipν(Sn-1),0<ν≤1,有 可得 對于E2,由于x∈Ck,y∈Bj,且j≤k-3,又因為Ω(x,y)∈L∞(Rn)×Lipν(Sn-1),應用Minkowski不等式可得 其中 因此對任意的x∈Ck,有 對任意的λ>0,設K0是滿足下列條件的最大正整數,有 故對任意的k>K0,有 因此,有 綜合E1,E2的估計,可得 故可得 至此,定理1證畢. 參考文獻: [1] STEIN E M. On the functions of littlewood-paley[J]. Trans Amer Soc, 1958, 88: 430-466. [2] TORCHINSKY A, WANG S. A note on the Marcinkiewicz integral[J]. Colloquium Math, 1990, 60/61: 235-243. [3] 王婭昕. 關于Marcinkiewicz積分交換子的一點注記[J]. 浙江大學學報 (理學版), 2003, 30 (6): 606-608. [4] MO H X, LU S Z. Boundedness of generalized higher commutators of Marcinkiewicz integrals[[J]. Acta Math Scientia, 2007, 27B (4): 852-866. [5] 邵旭馗, 陶雙平. 帶變量核的Marcinkiewicz積分交換子的加權Lipschitz估計[J]. 系統科學與數學, 2012, 37 (2): 915-921. [6] 邵旭馗, 王素萍. 帶變量核的分數次積分交換子在加權Morrey-Herz空間的有界性[J]. 應用數學學報, 2014, 37 (3): 497-506. [7] XUE Q Y, YABUTAK A.L2-Boundedness of Marcinkiewicz integrals along surfaces with variable kernels[J]. Journal of Inequalities and Applications, 2007: 1-14. [8] 王素萍, 邵旭馗. 變量核Marcinkiewicz積分交換子在齊次Morrey-Herz空間中的有界性[J]. 系統科學與數學, 2013, 33 (12): 1498-1506. [9] 邵旭馗, 王素萍. 帶變量核的分數次積分算子在加權Morrey空間上的有界性[J]. 安徽大學學報 (自然科學版), 2015, 39 (1): 21-24. [10] 王素萍, 岳曉紅, 邵旭……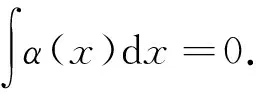
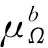
1 定理的證明