三維與二維結合地源熱泵地下換熱器復合數值模型

T.M.Eikevik

(1 上海交通大學機械與動力工程學院 上海 200240； 2 挪威科技大學 特隆赫姆 7491)

鑒于我國面臨的嚴峻能源和碳排放形勢[1]，地源熱泵技術以低能耗特點如今成為傳統空調系統的替代方案之一。地埋管換熱器作為地源熱泵系統最主要的部件之一備受研究者關注并由此演化出諸多模型。L. R.Ingersoll等[2]提出的無限線熱源模型屬于最早期的地埋管模型。該模型計算簡便但只考慮了土壤中徑向的熱交換而忽略了軸向的熱交換。而這一點被D. Marcotte 等[3-5]證明了重要性。此外，無限線源模型鑒于其積分式特點只適用于相對管徑較小的場合[6]。另一種廣泛使用的解析模型是L.Ingersioll等[7-9]提出的無限圓柱熱源模型。該模型由無限線熱源模型發展而來，并繼承了無限線熱源模型純熱傳導假設和不考慮軸向熱交換的特點，因而同樣不適用于長期模擬[10]。為了彌補這一缺陷，P. Eskilson[11]引入了有限線熱源模型。P. Eskilson的模型考慮了軸向換熱及多管疊加的熱效應，但其缺陷在于計算相對耗時，且和其他解析模型一樣設定沿管長的熱流密度為一定值。

相較于解析模型，數值模型通常有高精度和對應實際工程場景可定制的特點。然而，數值模型尤其是三維數值模型對計算量的要求極高[12-13]。因此多篇論文采用了不同方法來降低計算耗時，這一嘗試主要分成普通三維模型和準三維模型兩類：一類是以T.Y.Ozudogru 等[14]為代表的普通三維模型，該模型通過一維線性單元來簡化模擬過程卻刻意忽略了管內液體的流動。不考慮流動的影響在流速較大、管長較長的情況下尤為明顯。另一類是以Li Zhongjian[15]為代表的準三維模型，該模型考慮到模型的對稱性因而只計算了其中一邊。這一類準三維模型[16-18]的主要特點是不考慮地表和埋管底部的影響直接把模型簡化為水平二維模型，同樣不能反映軸向熱交換，因而不適用于長期模擬。

綜上所述，這些為了追求減少計算耗時的簡化削弱了原三維模型的準確性。很多簡化只是局部性的，不能從根本上改變三維模型耗時的特點，無法滿足不規則管群溫度分布的模擬。由此可見，單獨一個的三維模型或二維模型不能很好地模擬真實氣候條件下的實際問題。

本文提出了一個三維與二維結合地源熱泵地下換熱器復合數值模型，能引入實際氣候數據的影響，獲得不規則管群周邊溫度場分布情況，且提高計算效率。在新建的復合模型中，三維模型導出的模擬結果被用作二維模型輸入的邊界條件。結合兩者的復合模型既發揮了三維模型準確性高的優點，又通過二維模型顯著降低了管群模擬的運算量。

1 換熱器模型的建立

復合模型由一個三維模型和一個二維模型組成。三維模型由兩組U形管、管內流體、回填材料、管外及表層土壤組成。U形管外土壤的計算區域半徑為2 m，計算區域深度距U形管底部2 m，具體結構如圖1所示，換熱模型參數如表1所示。二維模型可根據實際管群分布建立。實際管群分布為呈直角分布的兩組矩形埋管陣列，管外土壤的計算半徑為4 m，如圖2所示。選擇陣列中最具代表性的共27根地埋管組成的直角區域進行建模。為進一步簡化，二維模型采用單位管化，相應的參數也做了適當調整[19]，相應的網格如圖3所示，其中離U形管較近的網格較為緊湊，離U形管較遠的網格較為稀疏。復合模型中，三維模型在運行狀態下不同深度的鉆孔壁溫度模擬結果可視為二維模型的鉆孔壁溫度；其導出的鉆孔壁暫態溫度序列可被植入二維模型的邊界條件函數。因此，在計算管群埋管區域某一個深度范圍內的溫度分布時可以針對性的選取三維模型該范圍內等間距的輸出結果作為輸入邊界條件帶入二維模擬，可避免運行三維管群模型需要計算每一層網格所負擔的龐大計算量。換熱器模型建立過程中所作假設如下：1)地表溫度隨大氣溫度變化；2)管內換熱流體溫度僅隨流動方向一維變化；3)土壤及回填材料為物性均勻；4)材料物性參數在模擬過程中保持不變；5)管間的相互影響僅限于垂直于U形方向。

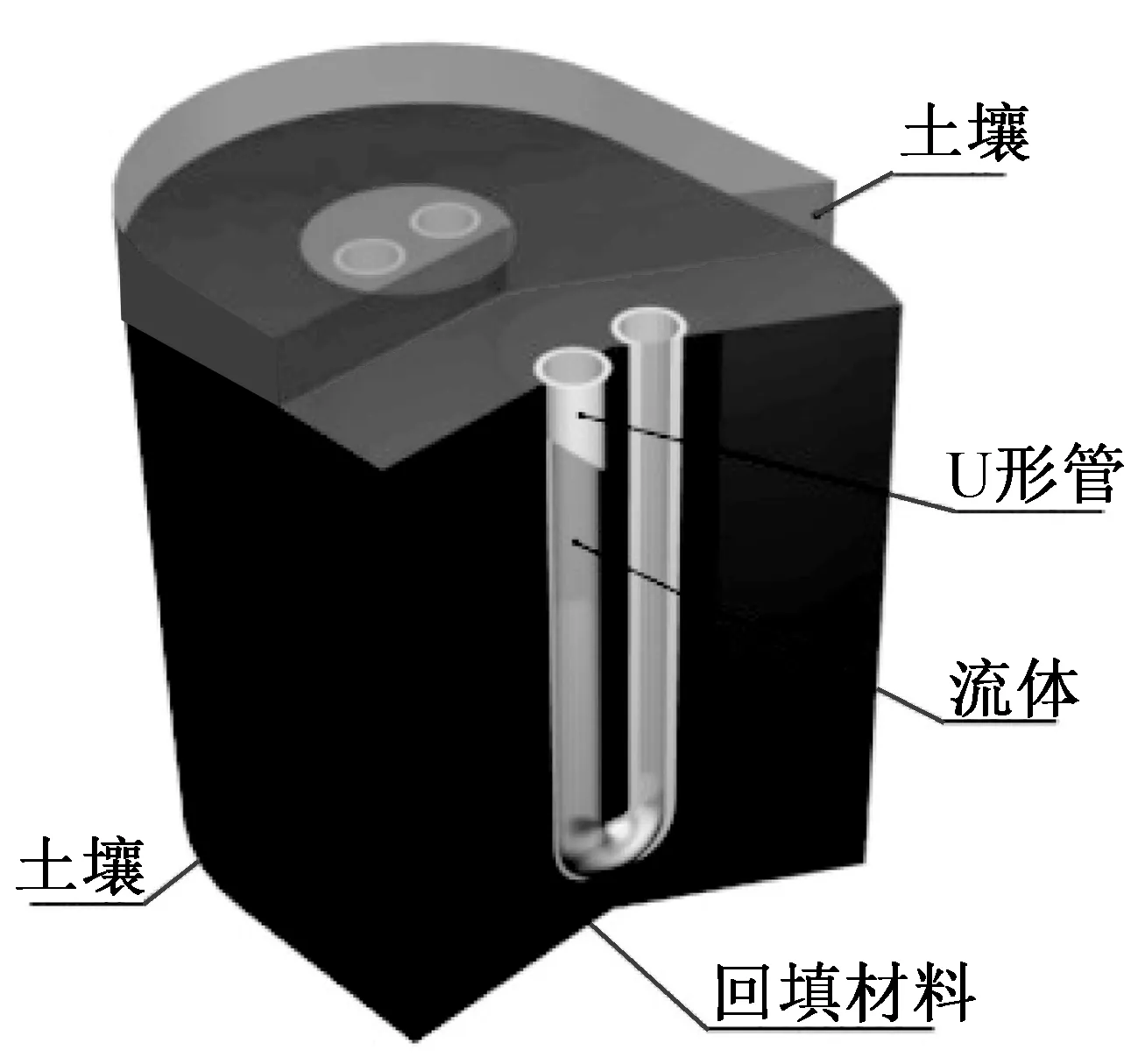
圖1 三維模型示意圖Fig.1 Schematic diagram for the 3D model

系統在運行狀態下流體暫態的總換熱量等于因軸向流動引起的熱量變化與徑向導熱引起的換熱量之和，管壁與流體邊界上的能量平衡方程為：

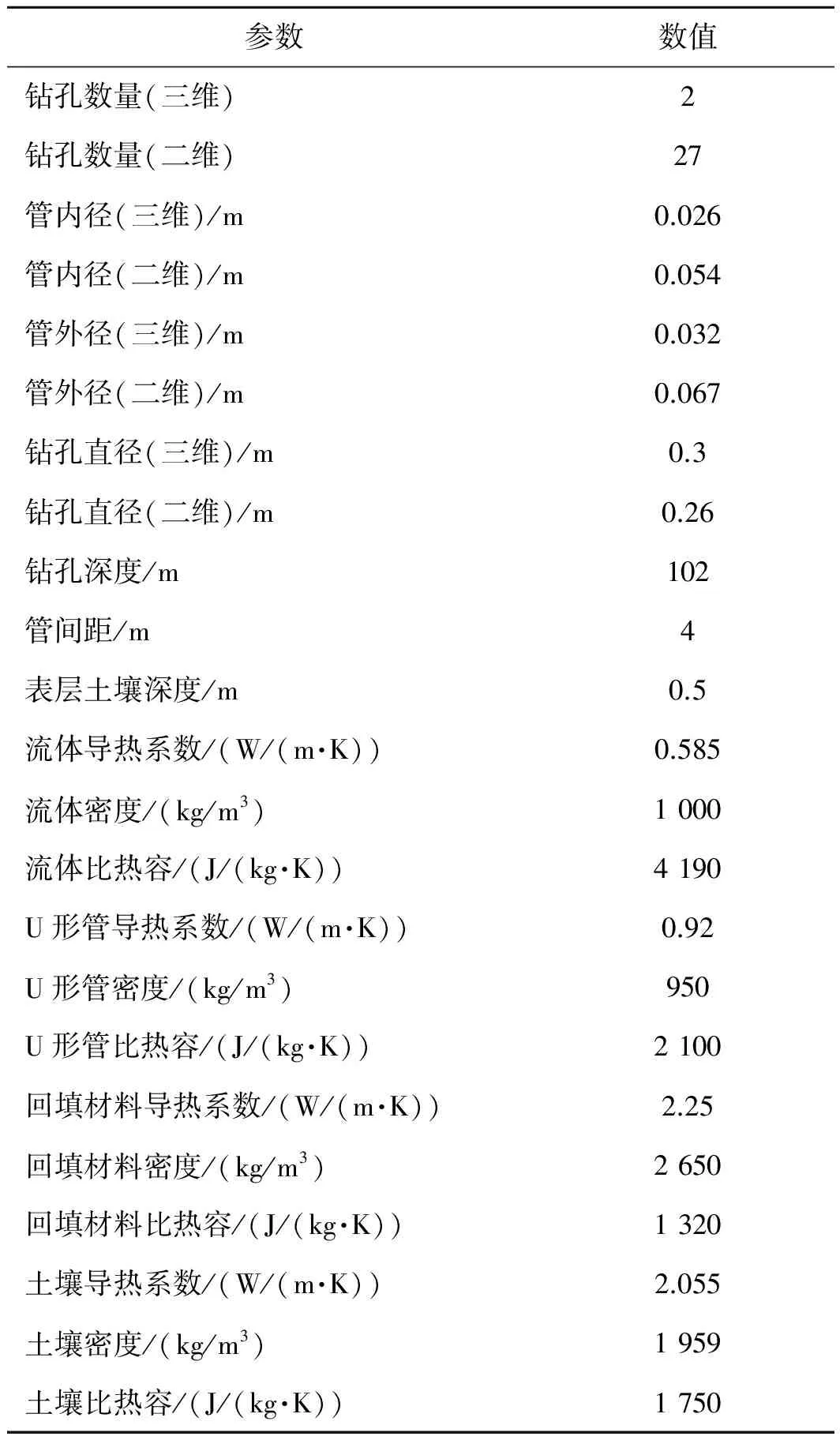
(1)

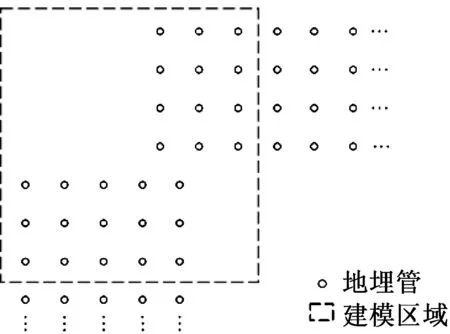
圖2 二維管群模型示意圖Fig.2 Schematic diagram of the boreholes distribution of the site in Hangzhou

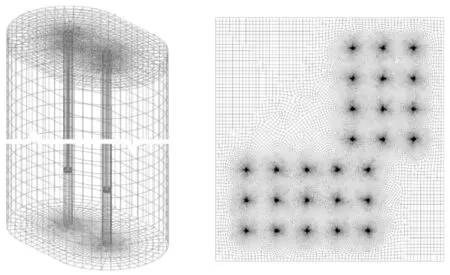
圖3 三維及二維網格模型Fig.3 The numerical mesh used to represent 3D and 2D model

系統停機狀態下流體暫態的總換熱量僅受到徑向的導熱的影響，其平衡方程為：

(2)

在U形管，回填材料和土壤內部的能量平衡方程為：

(3)

土壤的熱力學能初值設為零，變化方程為：

(4)

式中：T為溫度，K；τ為時間，s；m為質量，kg；r為半徑，m；z為深度，m；u為流速，m/s；α為熱擴散系數，m2/s；ρ為流體的密度，kg/m3；c為比熱容，J/(kg·K)；h為表面傳熱系數，W/(m2·K)；下標w，p，f，s分別指代流體、U形管、回填材料以及土壤；下標pi，po，b，in分別指代U形管內、外管壁、鉆孔壁及入口坐標位置。

假定各接觸面緊密結合，土壤表面的溫度，進水口的溫度和速度均分別由溫度函數序列Tudf(τ)和速度函數序列uudf(τ)給出。邊界上的溫度關系及輸入條件為：

(5)

(6)

歷史氣候數據的獲取有兩種途徑，國家氣象局的網站或使用氣象站數據。如果都沒有，可以考慮建立氣溫的理想化周期波動曲線：

T(τ)=0.5Tmcos(2×10-7τ+φm)+

0.5Tdcos(2×10-7τ+φd)+Tavg

(7)

式中：τ為時間，s；Tm，Td分別為年周期及日周期溫差,K；φm，φd分別為年周期及日周期的相位；Tavg為當地年平均氣溫，K。

二維模型傳熱方程的極坐標表達式為：

(8)

式中：θ為角度，(°)；k為導熱系數，W/(m·K)。三維模型在運行狀態下不同深度的孔壁溫度模擬結果可視為二維模型的鉆孔壁溫度，因而其導出的鉆孔壁暫態溫度序列Tudf′(τ)可構成二維模型的鉆孔壁輸入邊界條件：

Ts(τ)|r=rb=Tudf′(τ)

(9)

同時三維模型導出的不同深度穩定的土壤初始溫度構成不同深度二維模型土壤初始溫度。

三維及二維模型模擬流程如圖4所示。

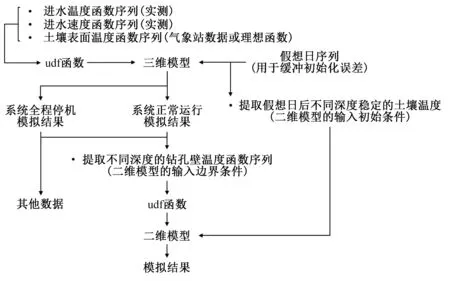
圖4 三維及二維模型模擬流程Fig.4 The simulation process of 3D and 2D model

2 換熱器模型的驗證

為了驗證本文采納的三維模型暫態模擬方法的準確性，此處比照B.A.Beier等[20]提出的沙盒實驗建立文獻中同尺寸的地下換熱器暫態數值模型。模型采用的具體幾何與熱物性參數見表2，同時模型采用了與實驗相同的入口流速和溫度作為輸入邊界條件。模擬預測的出水口暫態溫度文與文獻中傳感器實測的出水口溫度對比如圖5所示。其平均絕對比例誤差(MAPE)為3.13%，平均絕對誤差(MAE)為0.416，相較傳感器在測量時隨機產生的標準差0.391 K，可認為所建立的三維模型能很好地反映實際情況。

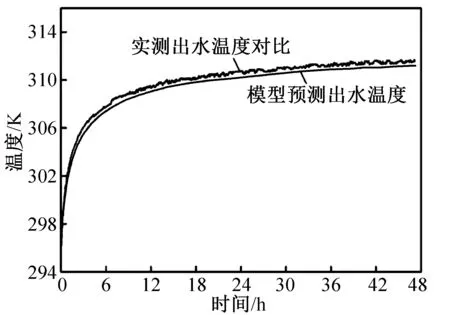
圖5 模型預測出水溫度與實測出水溫度對比Fig.5 Comparison for predicted and measured outlet temperature

3 模擬結果與分析

論文采納了杭州市內的氣象站數據，跨度為一個完整的供冷季、過渡季和供暖季。模型的模擬時間從2015年6月12日—2016年3月17日，期間分為供冷季、過渡季及供暖季。地源熱泵在供冷季和供暖季中分別向地下釋放熱量和冷量，在過渡季長時間處于停機狀態。從15年6月12日開始模擬直至16年3月17日的熱力學能與氣溫數據如圖6所示。地下換熱器模型采納的初始化條件為流體、U形管、回填材料和土壤各節點采用統一溫度設定為291.8 K，通過將第一步的邊界條件作為定值重復模擬50個假想日，可以有效緩沖初始化帶來的誤差影響。在模擬中第一個假想日的熱力學能增量為0.039 4 MJ，供冷季開始前最后一個假想日的熱力學能增量僅有0.001 9 MJ，熱力學能隨時間的斜率之比降至初始值的4.9%，近似于6月大氣條件下的土壤熱力學能自然增量的速度。表明經過50個假想日的前置穩定期后，土壤已基本達到適宜后續模擬運算的溫度分布。

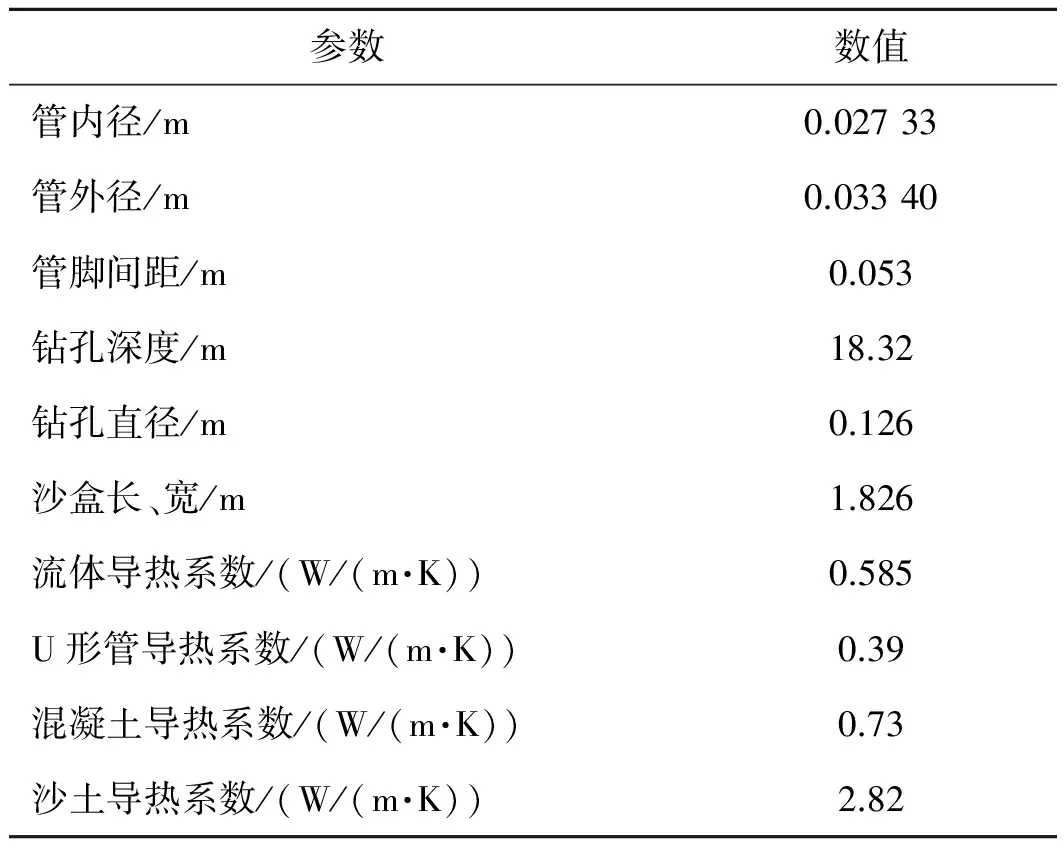
表2 沙盒實驗參數

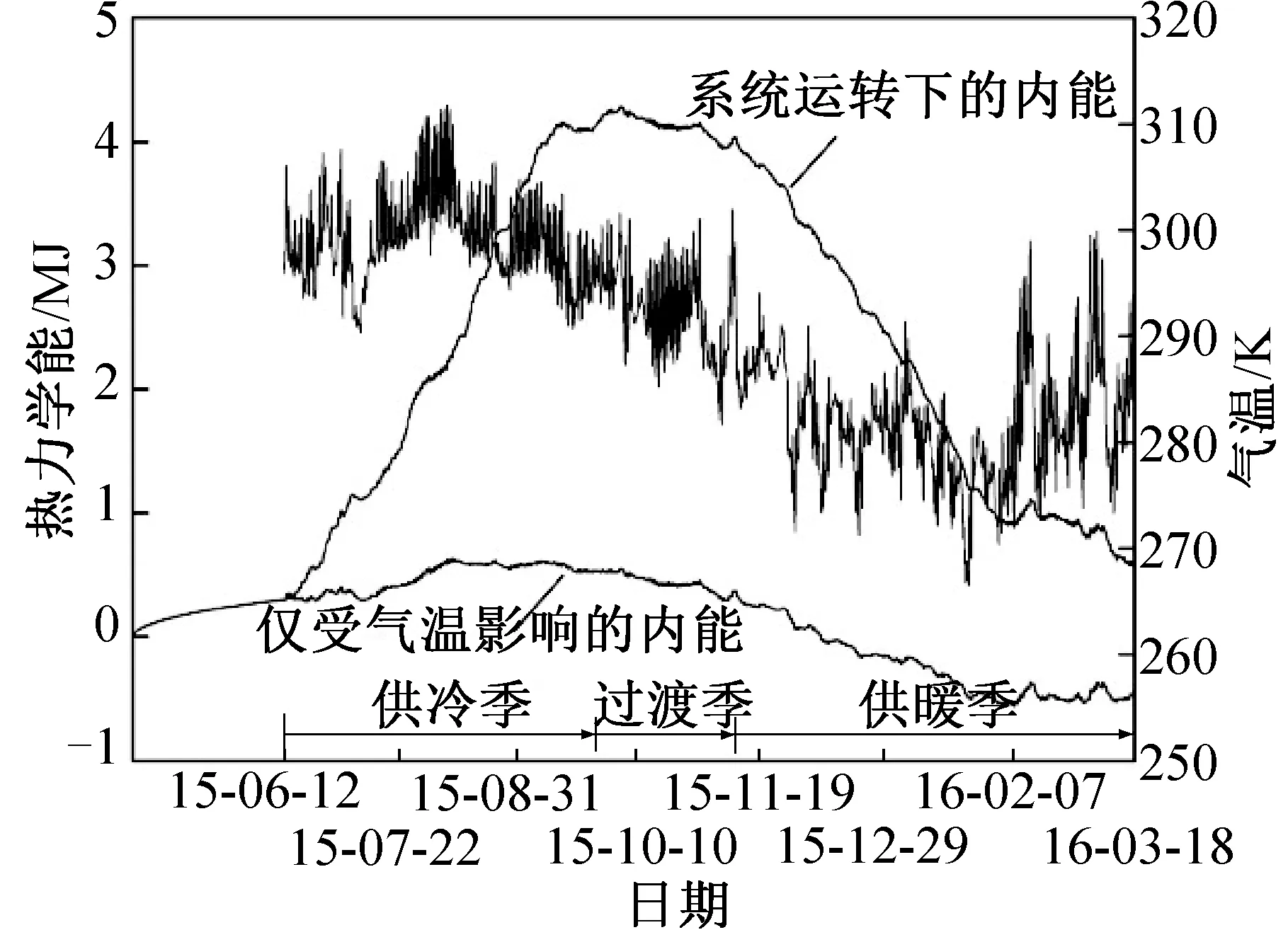
圖6 土壤熱力學能與氣溫對照數據Fig.6 Data of soil internal energy and air temperature

圖6中大氣溫度曲線在8月上旬(8月4日14∶00)達到峰值后開始下行并在一月下旬(1月16日6∶00)達到谷值。地埋管在供冷季向地下釋放熱量并在供暖季從地下抽取熱量。對應的土壤熱力學能曲線在供冷季上升，在過渡季中基本保持不變，并在供暖季開始后逐步下降。與僅受氣溫影響的熱力學能對比可見系統運轉下的內能曲線變化在供冷季和供暖季明顯更加陡峭。在供冷季結束后整個三維計算區域的熱力學能上升了3.96 MJ，平均溫升為1.09 K。一個供冷季、過渡季、供暖季結束后，整個三維計算區域的熱力學能上升了0.292 MJ，與僅受氣溫影響的情況相比，土壤的相對熱力學能增量為1.037 MJ，相對溫度增量為0.28 K，如圖7所示。這反映了長江三角洲地區每年對冷量的需求高于對熱量的需求，因而在年復一年的換熱過程后，將有大量的熱量被堆積在土壤中，進而影響地埋管換熱器的換熱效率。

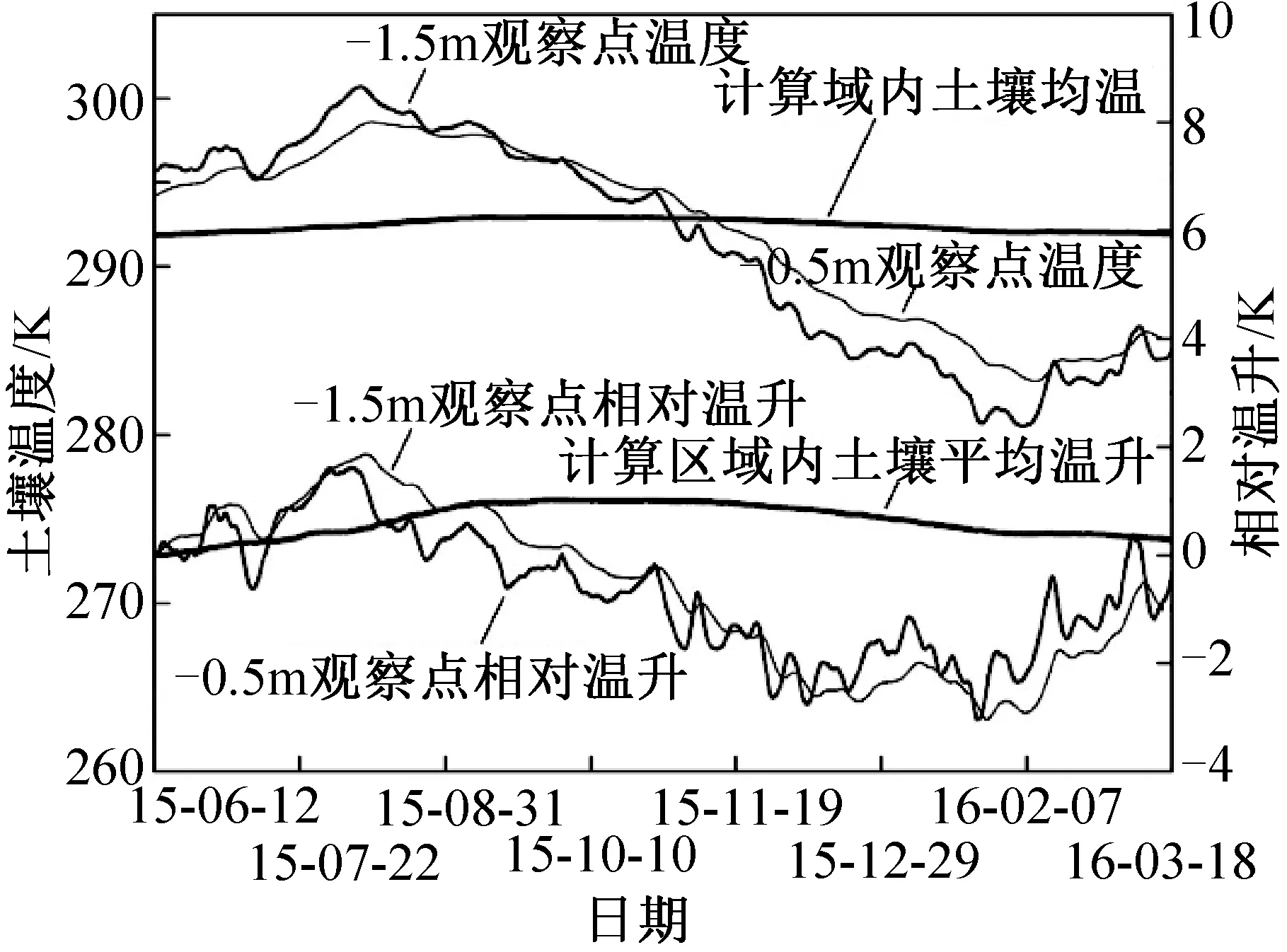
圖7 不同深度觀測點的土壤溫度Fig.7 The soil temperature at at different depth observation points

指定-0.5 m及-1.5 m的進出水管連線中心軸上的觀察點，考察其全年的溫度變化情況。-1.5 m的觀測點的平均溫度及和僅受氣溫影響情況下的相對溫升峰值滯后于-0.5 m的觀測點約2周的時間。計算區域內土壤的平均溫度和僅受氣溫影響情況下的相對溫升峰值滯后于-0.5 m的觀測點約9周的時間。說明沿埋管深度深的絕對溫度和相對僅受氣溫影響情況下的溫升曲線均在相位上滯后于沿埋管深度較淺的點。

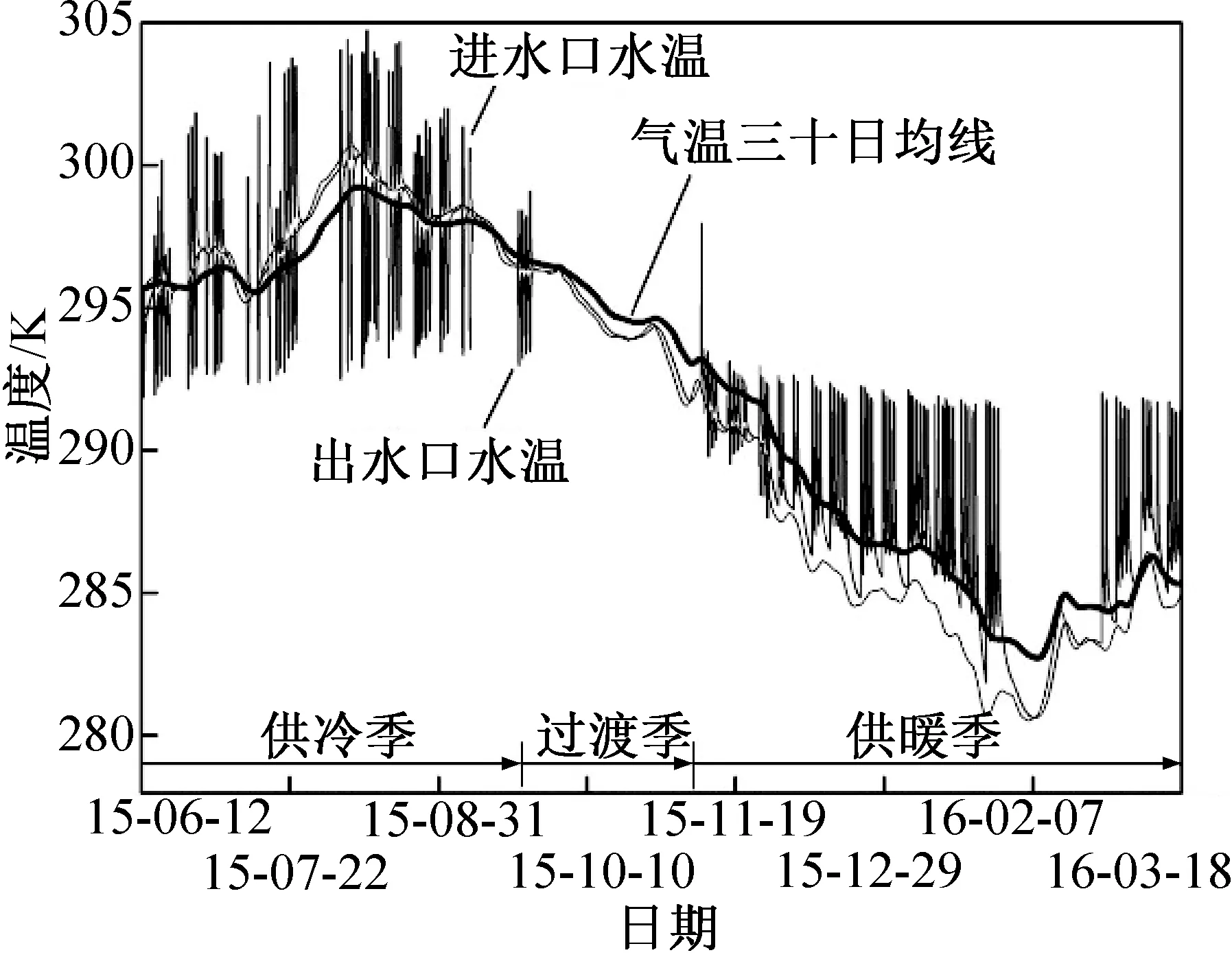
圖8 進出水口溫度對比Fig.8 Comparison of the inlet fluid temperature and outlet fluid temperature

杭州市內的地源熱泵系統在僅在需要供冷或供熱季節的工作時間開機，在多數周末、節假日停機。尤其在9月末到11月初這段氣溫適宜的過渡季期間，系統有較長的停機時段。在系統停機期間，土壤各點的溫度及進出口處的水溫僅受大氣及環境溫度的影響，顯示出較為平滑的曲線。由圖8整理得知，當系統運行時，整個供冷季地埋管的出水口水溫與同時刻氣溫溫差均值為-8.313 K，整個供暖季地埋管的出水口水溫與同時刻氣溫溫差均值為9.077 K。

圖9所示為在完整的供冷季、過渡季、供暖季結束后埋管周圍的溫度分布情況，埋管區域一側及轉角處受到熱堆積的最大影響半徑見表3。由表3可知，沿埋管深度越深受熱堆積影響的范圍越小，埋管區域在轉角處的熱堆積影響半徑顯著大于埋管區域一側的影響半徑，其影響半徑的比值隨深度減小，反映出不規則排列地埋管群的熱堆積在較深的地層的影響范圍更局限于其自身的排列形狀。通過用系統運轉條件下的截面平均溫度減去僅受大氣影響條件下的平均溫度可得不同深度截面的平均溫升，如圖10所示。-1 m深和-10 m以下的截面有不同的均溫變化規律，并且-1 m深度在整個供冷季的均溫峰值低于-10 m的均溫峰值。這一現象表現出與大氣的換熱在帶走土壤熱堆積尤其是表層土壤熱堆積方面的顯著影響。結合三維模型的模擬結果可知，系統運轉所造成的熱堆積效應主要集中在7 m以下稍深的土壤層而非與大氣頻繁換熱的表層土壤(最大溫差0.5 K)。

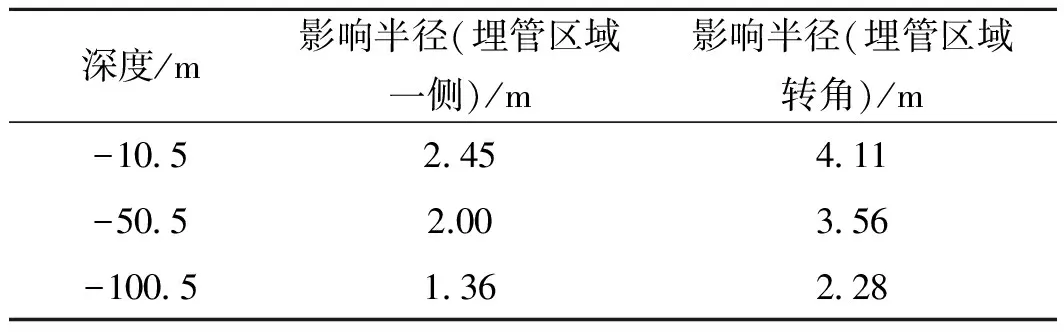
表3 不同深度處的最大影響半徑

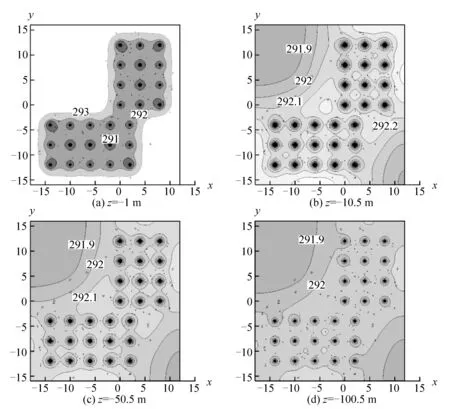
圖9 供暖季結束時不同深度的二維溫度分布Fig.9 Temperature distribution at different depth at March 17th, 2016

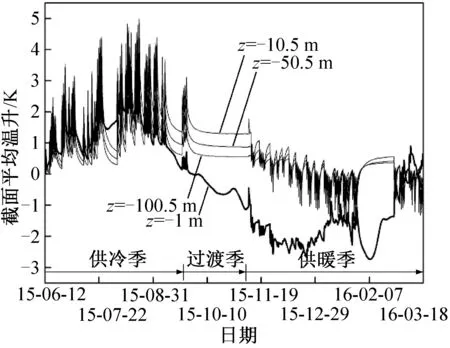
圖10 截面平均溫升隨不同深度的變化Fig.10 Cross section average increment of temperatureat changes with different depth

3 結論

本文建立了基于實際氣候條件下的三維與二維結合地源熱泵地下換熱器復合數值模型。實現了用較小的計算耗時處理模擬管群換熱的問題。相較于現有模型，新建立的復合模型利用三維模型的暫態模擬結果作為二維模型輸入的邊界條件，進而在降低管群運算復雜度的同時保證了精確性。案例中，采用了杭州市內的實測數據，模擬時間為2015年6月12日—2016年3月17日，跨度為一個完整的供冷季、過渡季和供暖季，主要結論如下：

1)當計算三維換熱時，不需要采用設置初始溫度的方法，僅需設定初始氣溫，將第一步的邊界條件作為定值重復模擬50個假想日的時長作為緩沖，可將熱力學能隨時間的日均斜率降至初始值的4.9%，有效沖抵了初始化時全部節點設置同一個初始溫度帶來的誤差干擾。

2)影響半徑為2 m以內的土壤在模擬一個完整的供冷季、過渡季和供暖季后的熱力學能增量為0.292 MJ，相較僅受氣溫影響的土壤的相對熱力學能增量為1.037 MJ，相對溫度增量為0.28 K。該增量反映出長三角地區用戶對冷量的需求高于對熱量的需求，因此釋放到土壤中多余的熱量將隨時間逐步堆積，對換熱效率產生不利影響。

3)沿埋管深度深的絕對溫度和相對僅受氣溫影響情況下的溫升曲線均在相位上滯后于沿埋管深度較淺的點。在進出水口連線中心軸上-1.5 m的觀測點的平均溫度及和僅受氣溫影響情況下的相對溫升峰值滯后于-0.5 m的觀測點約2周的時間。計算區域內土壤的平均溫度和僅受氣溫影響情況下的相對溫升峰值滯后于-0.5 m的觀測點約9周的時間。

4)系統運行條件下，整個供冷季地埋管的出水口水溫與同時刻氣溫溫差均值為-8.313 K，整個供暖季地源熱泵的出水口水溫與同時刻氣溫溫差均值為9.077 K。

5)系統運轉造成的熱堆積效應主要集中在7 m以下稍深的土壤層而非與大氣頻繁換熱的表層土壤。埋管區域在轉角處的熱堆積影響半徑大于其一側的影響半徑，且其絕對值與比值均隨深度的增大而減少，說明不規則排列地埋管群的熱堆積的影響范圍在越深的地層越局限于自身的排列形狀。

[1] 中華人民共和國國家統計局. 2014年中國統計年鑒[M].北京: 中國統計出版社,2014：54-56. (National Bureau of Statics of China. China statistical yearbook in 2014[M]. Beijing: China Statistic Press, 2014：54-56.)

[2] INGERSOLL L R, PLASS H J. Theory of the ground pipe heat source for the heat pump[J].Heating Piping & Air Conditioning, 1948, 54(7): 339-348.

[3] MARCOTTE D, PASQUIER P, SHERIFF F, et al. The importance of axial effects for borehole design of geothermal heat-pump systems[J]. Renewable Energy, 2010, 35(4): 763-770.

[4] ZENG H Y, DIAO N R, FANG Z H. A finite line-source model for boreholes in geothermal heat exchangers[J]. Heat Transfer—Asian Research, 2002, 31(7): 558-567.

[5] MOLINA-GIRALDO N, BLUM P, ZHU K, et al. A moving finite line source model to simulate borehole heat exchangers with groundwater advection[J]. International Journal of Thermal Sciences, 2011, 50(12): 2506-2513.

[6] YANG H, CUI P, FANG Z. Vertical-borehole ground-coupled heat pumps: A review of models and systems[J]. Applied Energy, 2010, 87(1): 16-27.

[7] INGERSIOLL L, ZOBEL O J, INGERSOLL A C. Heat conduction: with engineering geological and other applications[M]. US: University of Wisconsin Press, 1954.

[8] KAVANAUGH S P. Simulation and experimental verification of vertical ground-coupled heat pump systems[D].US: Oklahoma State University Stillwater, 1985.

[9] CARSLAW H S, JAEGER J C. Conduction of heat in solids[M]. Oxford: Clarendon Press, 1960.

[10] REES S J, HE Miaomiao. A three-dimensional numerical model of borehole heat exchanger heat transfer and fluid flow[J]. Geothermics, 2013, 46: 1-13.

[11] ESKILSON P. Thermal analysis of heat extraction boreholes[M]. 1987.

[12] HE Miaomiao, REES S J, SHAO Li. Simulation of a domestic ground source heat pump system using a three-dimensional numerical borehole heat exchanger model[J]. Journal of Building Performance Simulation, 2011, 4(2): 141-155.

[13] HE Miaomiao. Numerical modelling of geothermal borehole heat exchanger systems[D].Leicester: De Montfort University, 2012.

[14] OZUDOGRU T Y, OLGUN C G, SENOL A. 3D numerical modeling of vertical geothermal heat exchangers[J]. Geothermics, 2014, 51: 312-324.

[15] LI Zhongjian. A new constant heat flux model for vertical U-tube ground heat exchangers[J]. Energy and Buildings, 2012, 45: 311-316.

[16] ZHANG Linfeng, ZHANG Quan, HUANG Gongsheng. A transient quasi-3D entire time scale line source model for the fluid and ground temperature prediction of vertical ground heat exchangers (GHEs)[J]. Applied Energy, 2016, 170: 65-75.

[17] MA Weiwu, LI Min, LI Ping, et al.New quasi-3D model for heat transfer in U-shaped GHEs (ground heat exchangers): Effective overall thermal resistance[J]. Energy, 2015, 90: 578-587.

[18] WETTER M, HUBER A. Vertical borehole heat exchanger EWS Model[J]. Trnsys Type, 1997, 451.

[19] GU Y, O′NEAL D L. Development of an equivalent diameter expression for vertical U-tubes used in ground-coupled heat pumps[J]. Ashrae Transactions, 1998, 104(2): 347-355.

[20] BEIER R A, SMITH M D, SPITLER J D. Reference data sets for vertical borehole ground heat exchanger models and thermal response test analysis[J]. Geothermics, 2011, 40(1): 79-85.