Cu,O共摻雜AlN晶體電子結構與光學性質研究?

程麗 王德興 張楊 蘇麗萍 陳淑妍 王曉峰 孫鵬 易重桂

(哈爾濱工程大學理學院,纖維集成光學教育部重點實驗室,哈爾濱 150001)

1 引 言

AlN是近年來深受人們關注的一種新型直接帶隙寬禁帶化合物半導體材料,其禁帶寬度Eg約為6.2 eV[1,2].由于AlN具有禁帶較寬、介電常數低以及與硅相近的熱膨脹系數,可作為微電子器件的基底材料;AlN良好的壓電性質與較高的表面聲速使其可作為GHz聲表面波裝置的壓電材料[3?5];AlN也是制造紫外發光二極管光源的材料[6].另外,AlN原料充足,生產成本相對較低,可應用于多種工業領域.

現在,AlN的制造技術得到了高速發展[7?9],但AlN的高效率p型摻雜問題還未解決.對AlN晶體而言,n型摻雜比較容易實現,p型摻雜效率低主要是由于p型雜質溶解度較低,離化能過大及本身缺陷的自補償效應造成的[10],進而影響了AlN基的固態發光器件實用化.因此,制備高效的p型層是研究AlN在光電器件領域廣泛應用的重點.p型AlN已通過摻入Be,Cu,Mg,Zn,Ag等得以實現[11?16],但摻雜效率較低.為獲得高效的p型AlN,學者們對共摻雜方法進行了探討,認為共摻雜方法的優點在于:1)施主、受主間的強吸引可克服受主間的互相排斥,增加受主在AlN晶體中的摻雜數量;2)施主、受主間的吸引可形成“受主-施主-受主”復合體,從而降低受主能級、提高施主能級,進而提高空穴濃度.Zunger等證實了Be和O兩種高活性原子在III族氮化物中的共摻雜反應[17],袁娣等通過第一性原理計算表明Be和O共摻雜可提高摻雜濃度和系統的穩定性[18];Wu等認為Mg和O共摻雜可提高AlN晶體的空穴濃度[19];Korotkov等研究了Mg和O共摻p型GaN的電子特性[20].非磁性元素Cu摻雜AlN具有較好的半金屬鐵磁性,且Cu摻雜表現為p型摻雜.為獲得更高濃度的p型Cu摻雜,本文對Cu和O共摻雜的AlN晶體進行理論計算及分析.基于密度泛函理論(DFT)的平面波超軟贗勢法,利用3×3×2模型計算了Cu和O共摻雜AlN的電子結構與光學特性,詳細分析Cu和O共摻雜對AlN晶體p型特性的影響,為實驗研究提供理論參考.

2 理論模型與計算方法

2.1 理論模型

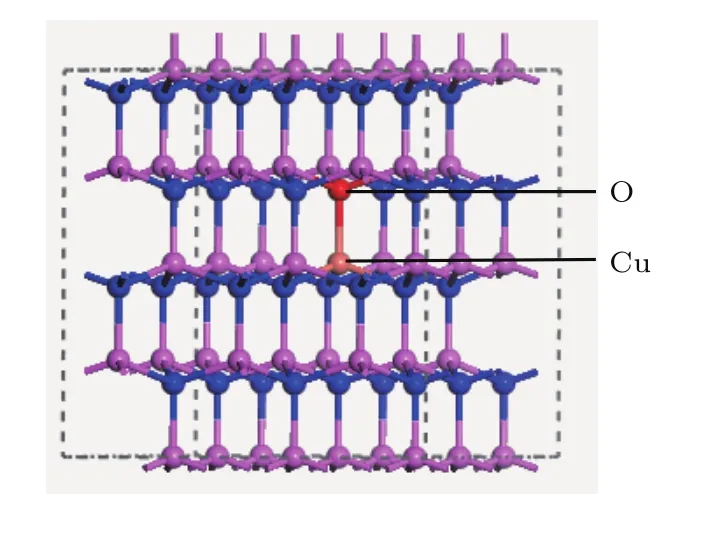
圖1 Cu和O共摻雜AlN超晶胞模型Fig.1.Supercell of Cu-O co-doped AlN.

2.2 計算方法

本文計算由從頭算量子力學程序CASTEP[22]完成.對未摻雜、Cu單摻雜與Cu和O共摻雜AlN(3×3×2)進行幾何結構優化,交換-關聯能采用廣義梯度近似GGA-PBE進行校正,離子實與價電子之間的相互作用勢采用超軟贗勢(ultrasoft pseudopotential,USP)來描述.平面波截止能取450 eV,布里淵區積分使用4×4×3的k點對全Brillouin求和,迭代時收斂精度設為1×10?5eV/atom,作用到原子上的力小于0.3 eV/nm,內應力收斂精度設為0.05 GPa,最大位移收斂精度設為1×10?4nm.幾何結構優化后上述四參數達到或高于收斂條件.

3 計算結果與討論

3.1 幾何結構優化結果

為了分析摻雜對AlN性質的影響,本文對Cu和O摻雜前后AlN晶體超胞進行幾何結構優化.計算得到的晶格參數、總能量、截斷能與形成能如表1所列.其中a,c為單胞的晶胞參數;V0為超晶胞的體積;E為對體系進行幾何優化收斂時對應的體系總能量,反映了結構的穩定程度;Eg為禁帶寬度;Ef為形成能.從表1可以看出,計算結果與實驗結果符合得很好,表明參數選取與計算方法合理,可繼續進行其他性質的計算.摻雜后晶格體積比純AlN晶體稍有增大,因為Cu的離子半徑為0.077 nm,比Al的離子半徑0.054 nm大,當離子半徑大的Cu替代離子半徑小的Al時,一定程度上破壞了晶格周期性,造成晶格畸變,晶格體積增大;O的離子半徑為0.14 nm,比N的離子半徑0.013 nm大,所以O摻雜也會使AlN的晶格體積變大.Cu和O共摻雜的整體效果是增大了AlN晶胞的體積.表1的能量計算結果顯示,Cu摻雜后體系能量降低,Cu和O共摻雜體系能量最低.Eg理論值與實驗值相比偏小,這是由于DFT屬于基態理論,它對多粒子系統的激發態在計算Eg時存在誤差[24],但并不影響對AlN及其摻雜體系電子結構和性質的理論分析.

表1 AlN摻雜前后的晶格常數、總能量、禁帶寬度與形成能Table 1.Lattice constant,total energy,band gap and formation energy of AlN before and after doped.

摻雜體系的形成能Ef是用來判斷不同原子摻雜難易的物理量,同時也可以表明雜質對該體系穩定性造成的影響,Cu單摻雜與Cu和O共摻雜AlN形成能Ef計算公式為:

式中EAlNCu,EAlNCuO為Cu單摻雜與Cu和O共摻雜AlN超胞系統的總能量;EAlN為未摻雜AlN超胞系統的總能量;μAl,μCu為Al原子與Cu原子在基態下對應為金屬相時每個分子的能量;μO,μN則為晶體相時O與N原子對應的能量,即溫度T=0時化學勢的大小.從表1形成能計算結果可知,Cu和O共摻雜體系比Cu單摻雜體系形成能降低,穩定性增加,這與總能量的計算結果符合.

3.2 電子結構分析

3.2.1 純AlN電子結構分析

為分析和比較摻雜對AlN電子結構的影響,先計算了純AlN的電子結構如圖2所示.圖2(a)能帶結構的計算結果表明AlN的帶隙較大,導帶底和價帶頂都位于Brillouin區的G點處,且與其他K點帶隙比較,G點帶隙最小,表明AlN是直接帶隙半導體.導帶底的態密度變化較大,說明導帶底電子有效質量大;價帶頂態密度變化較慢,說明價帶中空穴有效質量大.AlN的價帶由?15.5—?12.8的下價帶和?6.3—?0.3的上價帶組成,在價帶頂附近有簡并的重空穴、輕空穴和自旋-軌道耦合所分裂出的劈裂帶,與其他III-V族氮化物的能帶結構類似.由圖2的分波態密度可知,價帶主要是N原子2s態與2p態構成,價帶頂則主要由N原子2p態組成,導帶主要是Al原子3p態構成.從分態密度可知,AlN的離子鍵性質比較明顯,這和一些文獻中的計算結果一致[25,26].

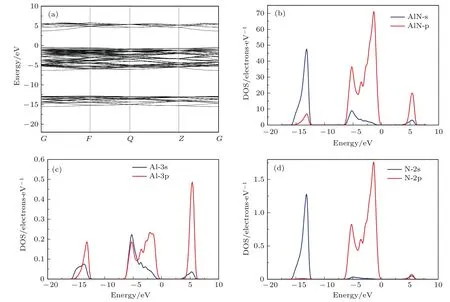
圖2 AlN的能帶結構與分波態密度 (a)能帶結構;(b)分波態密度;(c)Al的分波態密度;(d)N的分波態密度Fig.2.Energy band structure and PDOS of AlN:(a)Energy band structure;(b)PDOS of AlN;(c)PDOS of Al;(d)PDOS of N.

3.2.2 Cu摻雜AlN電子結構分析

為討論Cu和O共摻雜AlN的電子結構,先優化了Cu摻雜AlN晶體,其能帶結構及分波態密度如圖3所示.從圖3(a)可知,價帶頂部與導帶底部都在布里淵區G點處,表明摻雜Cu后AlN仍是直接帶隙半導體.對比圖3與圖2的分波態密度可知,Cu摻雜AlN的下價帶主要由N原子的2s態組成,導帶主要由Al原子的3p態組成,與未摻雜AlN相比無變化.主要變化來自上價帶,上價帶主要由Cu原子的3d態與N原子的2p態組成,對比圖3(d)和圖3(e)可知,Cu 3d態有幾個峰值與N 2p態相對應,費米能級附近的電子態密度也主要來自Cu 3d和N 2p態,且二者形狀相似,說明Cu 3d與N 2p電子間有較強的軌道雜化.Cu摻入后Al的態密度變彌散,沿高能方向擴展;同時價帶頂越過費米能級形成簡并態,在價帶頂附近存在多余的空穴,說明Cu摻雜可獲得p型AlN.但雜質能級中空穴間的互相作用導致其局域在價帶頂附近,費米能級附近空穴增加,原子間排斥作用增強,使Cu摻雜濃度低,摻雜系統不穩定,因此單摻雜Cu較難實現理想的p型AlN晶體.

圖3 Cu摻雜AlN的能帶結構與分態密度 (a)能帶結構;(b)分態密度;(c)Al的分態密度;(d)N的分態密度;(e)Cu的分態密度Fig.3.Energy band structure and PDOS of Cu doped AlN:(a)Energy band structure;(b)PDOS of Cu doped AlN;(c)PDOS of Al;(d)PDOS of N;(e)PDOS of Cu.

3.2.3 Cu與O共摻雜AlN電子結構分析

圖4為Cu與O共摻雜AlN的能帶結構與分波態密度.對比圖3可知,O原子摻入后,其2s態在?19 eV附近形成一條能帶,此能帶離價帶較遠,對價帶的電子分布無影響;Al原子分波態密度峰值升高,價帶和導帶均向低能方向移動;N原子的態密度在價帶頂處降低,價帶與導帶移向低能區;Cu的態密度比單摻雜時有所加寬,費米能級處態密度峰值降低,價帶及導帶也均向低能方向移動.Cu與O共摻雜AlN的費米能級進入價帶頂,使其價帶頂附近存在多余的空穴,于價帶頂形成雜質能級,且雜質能級具有較強的局域態,這是N和O原子的2p態與Cu 3d態軌道雜化的結果.因為O原子電負性比N原子強,Cu 3d態電子偏向與O成鍵,進而Al—N鍵增強、Cu—N鍵減弱,N價電荷分布偏向Al而偏離Cu,因此Cu與N間原子軌道交疊區域和費米能級處態密度重疊減小,降低Cu的受主特性,費米能級附近Cu 3d軌道與臨近O 2p軌道雜化增強.O原子不是p型材料的有效復合中心,主要起到對Cu原子的激活作用.共摻雜后Cu與O的吸引作用可克服Cu原子間的互相排斥,能有效提高受主摻雜濃度與系統的穩定性,Cu與O共摻雜可實現p型AlN的高濃度摻雜.

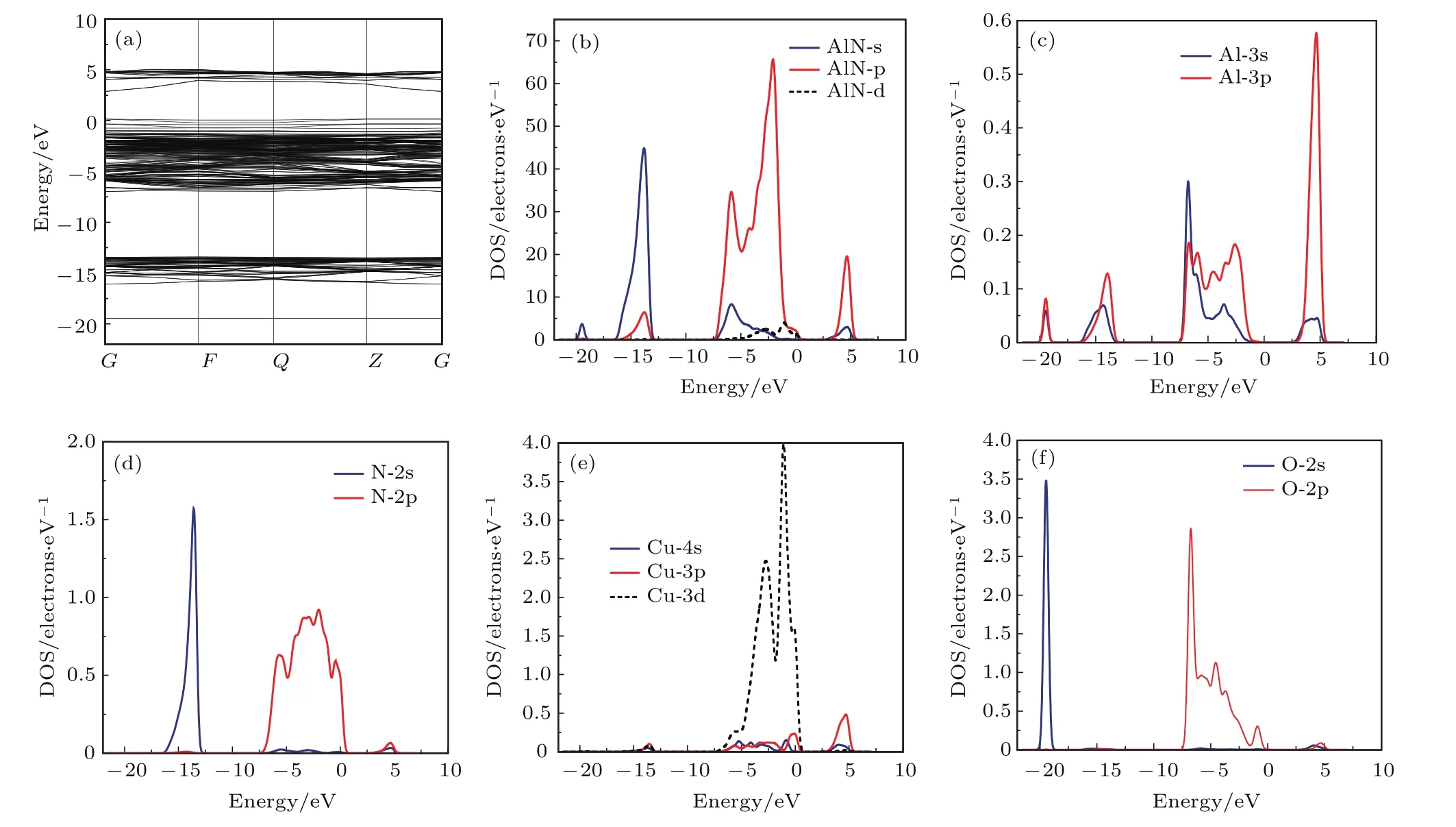
圖4 Cu與O共摻雜AlN的能帶結構與分態密度 (a)能帶結構;(b)分態密度;(c)Al的分態密度;(d)N的分態密度;(e)Cu的分波態密度;(f)O的分波態密度Fig.4.Energy band structure and PDOS of Cu-O co-doped AlN:(a)Energy band structure;(b)PDOS of Cu-O co-doped AlN;(c)PDOS of Al;(d)PDOS of N;(e)PDOS of Cu;(f)PDOS of O.

3.3 Cu與O共摻雜AlN的光學性質分析

為研究Cu與O共摻雜AlN的光學性質,對Cu與O摻雜前后AlN晶體的介電函數、復折射率函數和光吸收譜進行了計算與分析.計算光學性質時,采用剪刀算符對能帶帶隙進行了修正,剪刀算符的取值由帶隙的理論計算值與實驗值的差值決定,本文剪刀算符取值為2.07 eV.線性響應范圍內半導體光學性質可以用復介電函數ε(ω)=ε1(ω)+iε2(ω)計算得出,其與材料的電子結構關系密切.晶體的介電函數、吸收系數等可根據Kramers-Kronig色散關系及電子躍遷概率的定義導出.介電函數實部ε1(ω)與虛部ε2(ω)的計算公式如下[27]:

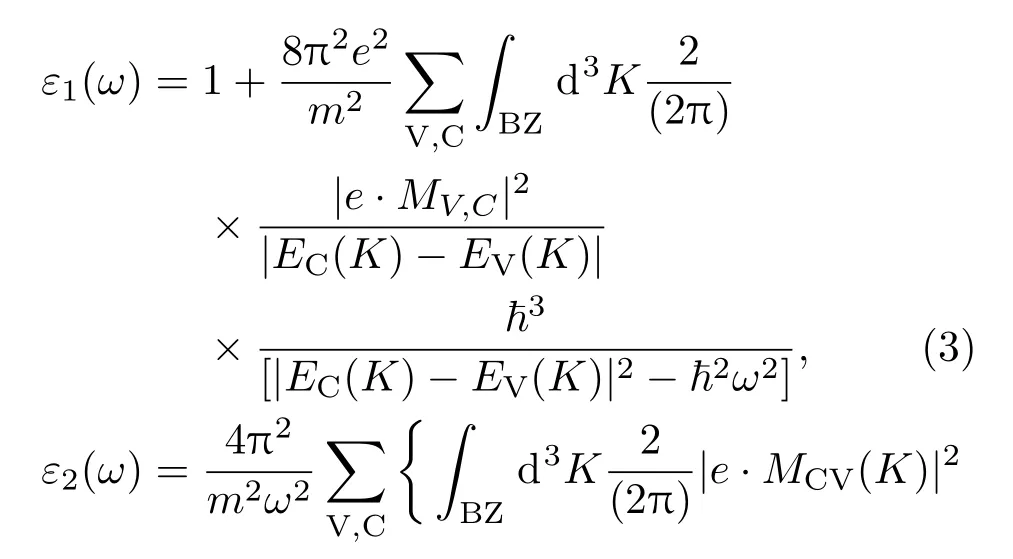
式中C,V代表導帶、價帶;BZ表示第一布里淵區;?是狄拉克常量;K是倒格矢;ω是角頻率;|e·MCV(K)|2是動量矩陣元;EC(K),EV(K)代表導帶、價帶本征能級.

圖5(a)為Cu與O共摻雜前后AlN的介電函數虛部ε2,ε2是聯系帶間躍遷微觀物理過程與固體電子結構的橋梁,是電子在能級間躍遷的體現,對材料光學性質的研究很重要,ε2曲線介電峰的來源可通過能帶結構與態密度解釋.從圖5(a)可以看出,純AlN的介電函數閾能約為5.4 eV,這是基本吸收邊,當光子能量高于5.4 eV時ε2的值迅速上升.AlN的介電函數虛部有兩個特征峰,峰1與峰2分別對應能量為8.8 eV與12.7 eV.峰1對應直接躍遷閾,是N 2p電子向Al 3p態躍遷;峰2是AlN態密度圖中上價帶相對較弱的峰代表的能態與導帶能態間電子躍遷所致.摻入Cu原子后,在2.2 eV增加一較高的介電峰3,之前的兩個介電峰峰值減弱.峰3是價帶電子向雜質帶躍遷引起的,主要是N 2p態與Cu 3d態躍遷的結果.摻入Cu原子后峰1、峰2變低是由于引入雜質帶后能級間躍遷電子數目下降;摻入O原子后峰1、峰2繼續降低,峰3變強主要是O 2p態躍遷的結果.在低能區,Cu與O共摻雜AlN的光躍遷強度大于未摻雜和Cu單摻雜AlN,表明Cu與O共摻雜可改善AlN低能區的光學躍遷,增強電子在可見光區的光學躍遷.

圖5(b)為Cu與O共摻雜前后AlN的復折射率.未摻雜AlN能量低于5.4 eV與能量高于14.4 eV時復折射率虛部為零、實部接近常數,表明AlN在低、高頻區對電磁波吸收均較弱.Cu與O原子摻入后復折射率在低能區實部和虛部變化明顯,是由于摻雜后電磁波通過不同介質導致折射率發生變化,增加了體系對低頻電磁波的吸收.

圖5 Cu與O共摻雜前、后AlN的介電函數虛部(a)、復折射率(b)與吸收譜(c)Fig.5.Imaginary part of the dielectric function(a),refractive index(b)and energy loss spectrum(c)of AlN before and after doped.

圖5(c)是摻雜前后AlN的吸收譜,結果表明,純AlN晶體在可見光區無光吸收,因其禁帶寬度大于可見光的光子能量.Cu與O摻入后,因為禁帶中引入了雜質能級,增強了晶體在可見光區的光吸收.純AlN吸收邊與復折射率函數符合,吸收主峰的能量為9.9 eV.Cu與O摻入后于低能區出現一新吸收峰,與復折射率函數在低能區的變化相對應.與純AlN相比,摻雜Cu后吸收峰減弱,Cu與O共摻后更弱,因為摻雜后引入受主能級導致能級間躍遷電子數目下降.

4 結 論

基于密度泛函理論對純AlN,Cu單摻雜以及Cu與O共摻雜AlN電子結構和光學性質進行了計算與分析.結果表明:摻雜后晶格體積增大,系統能量降低;Cu單摻雜及Cu與O共摻雜后AlN仍屬于直接帶隙半導體;Cu摻入后Cu 3d電子與鄰近的N 2p電子之間有強烈的軌道雜化效應,但Cu單摻雜濃度不高,摻雜系統不穩定,較難實現理想的p型AlN晶體;Cu與O共摻雜后,Cu與O的吸引作用克服了Cu原子間的排斥作用,可提高摻雜濃度和系統穩定性,Cu與O共摻雜可實現p型AlN的高濃度摻雜.光學性質分析中,介電函數計算結果表明Cu與O共摻雜能夠改善AlN電子在低能區的光學躍遷特性,增強電子在可見光區的光學躍遷;復折射率計算結果顯示Cu與O摻入后電磁波通過不同的介質導致折射率發生變化,對低頻電磁波吸收增加.

[1]Li J,Nam K B,Nakarmi M L 2003Appl.Phys.Lett.83 5163

[2]Taniysu Y,Kasu M,Makimoto T 2004Appl.Phys.Lett.85 4672

[3]Chen S,You Z J 2016Tsinghua Univ.56 1061(in Chinese)[陳碩,尤政 2016清華大學學報 56 1061]

[4]Rodriguez-Madrid J G,Iriarte G F,Araujo D 2012Mater.Lett.66 339

[5]Shen L,Heikman S,Moran B 2001IEEE Electron Dev.Lett.22 457

[6]Ren Z,Sun Q,Kwon1 S 2007Phys.Status Solidi C4 2482

[7]Shen L H,Zhang X S 2016Chin.J.Lumin.37 927(in Chinese)[沈龍海,張軒碩 2016發光學報 37 927]

[8]Mokhov E,Izmaylova I,Kazarova O 2013Phys.Status Solidi C10 445

[9]Yan Z,Wu H L,Zheng R S B 2013Chin.Ceram Soc.32 1468(in Chinese)[閆征,武紅磊,鄭瑞生 2013硅酸鹽通報32 1468]

[10]Vande Walle C G,Stamp flC,Neugebauer J 1998J.Cryst.Growth189–190 505

[11]Han R L,Jiang S M,Yan Y 2017Chin.Phys.B26 027502

[12]Deng J Q,Wu Z M,Wang A L,Zhao R Y,Hu A Y 2014Chin.J.Comput.Phys.31 617(in Chinese)[鄧軍權,毋志民,王愛玲,趙若禺,胡愛元2014計算物理31 617]

[13]Zhang L M,Fan G H,Ding S F 2007Acta Phys.-Chim.Sin.23 1498(in Chinese)[張麗敏,范廣涵,丁少鋒 2007物理化學學報23 1498]

[14]Lin Z,Guo Z Y,Bi Y J 2009Acta Phys.Sin.58 1917(in Chinese)[林竹,郭志友,畢艷軍 2009物理學報 58 1917]

[15]Fan Y Q,He A L 2010Acta Phys.-Chim.Sin.26 2801(in Chinese)[樊玉勤,何阿玲2010物理化學學報26 2801]

[16]Zhang Y 2008Ph.D.Dissertation(Wuhan:Huazhong University of Science&Technology)(in Chinese)[張勇2008博士學位論文(武漢:華中科技大學)]

[17]Zunger A 2003Appl.Phys.Lett.83 57

[18]Yuan D,Huang D H,Luo H F 2012Acta Phys.Sin.61 147101(in Chinese)[袁娣,黃多輝,羅華鋒2012物理學報61 147101]

[19]Wu R Q,Shen L,Yang M,Sha Z D,Cai Y Q,Feng Y P 2008Phys.Rev.B77 073203

[20]Korotkov R Y,Gregie J M,Wessels B W 2001Appl.Phys.Lett.78 222

[21]Ishihara M,Li S J,Yumoto H,Akashi K,Ide Y 1998Thin Solid Films316 152

[22]Segall M D,Lindan P J D,Probert M J 2002J.Phys.14 2717

[23]Li J,Nam K B,Nakarmi M L 2003Appl.Phys.Lett.83 5163

[24]Anisimov V I,Aryasetiawan F,Lichtenstein A I 1997J.Phys.:Condens.Matter9 767

[25]Dong Y C,Guo Z Y,Bi Y J,Lin Z 2009Chin.J.Lumin.30 314(in Chinese)[董玉成,郭志友,畢艷軍,林竹 2009發光學報30 314]

[26]Gao X Q,Guo Z Y,Cao D X,Zhang Y F 2010Acta Phys.Sin.59 3418(in Chinese)[高小奇,郭志友,曹東興,張宇飛2010物理學報59 3418]

[27]Shen X C 1992Optical Property of Semiconductor(Beijing:Science Press)p24(in Chinese)[沈學礎 1992半導體光學性質(北京:科學出版社)第24頁]