不同信噪比下混沌系統弱信號檢測性能分析?

石 敏 陳迎春 虢應華

（1.水聲對抗技術重點實驗室 湛江 524022）（2.91388部隊 湛江 524022）

1 引言

混沌系統具有對與之內置信號頻差較小信號敏感，而對噪聲及與之內置信號頻差較大信號免疫的特點［1～5］，據此可以檢測待測信號中是否含有與混沌系統內置信號同頻的微弱信號［6～10］。

仿真中發現，混沌臨界狀態下輸入不同信噪比的信號其檢測性能是不一樣的，某些信噪比的信號輸入到混沌系統臨界狀態中可能不會引起系統狀態的變化，混沌系統檢測弱信號是有概率的，本文中引入檢測率用于表征混沌系統檢測弱信號的檢測性能，仿真還發現其檢測性能與選取的混沌臨界閾值及噪聲功率均有關。

2 混沌系統微弱信號檢測的基本原理

可用于任意頻率微弱信號檢測的duffing混沌檢測系統方程為

式中，ω和γ分別為混沌系統內置信號頻率和幅度；k為阻尼系數，一般取 k=0.5，（x-x3）為非線性項，x?和x?分別為x的一階和二階微分。

當混沌系統處于臨界狀態時，將帶有強噪聲的外界信號作為系統內部周期驅動信號的攝動引入混沌系統。噪聲雖然強烈，但只是局部地改變系統的相軌跡，很難引起系統的狀態遷移。而一旦輸入帶有與內置信號同頻率的信號成分，即使幅值很小，也會使系統的周期驅動信號的幅度增加而超過臨界值，導致混沌振子向大尺度周期狀態的迅速過渡，最后通過識別系統的狀態遷移將深陷在噪聲中的微弱周期信號檢測出來。這就是混沌振子能把深埋于噪聲背景中的微弱信號檢測出來的基本原理。

當式（1）處于混沌臨界狀態，即γ=γd時，加入與系統內置信號同頻率的含噪信號，得到式（2）所示的方程形式：

式中，n（t）為噪聲，a為待測信號的幅度，且a<< γd。

在式（2）中，令k=0.5，ω=1，a=0.01，n（t）的功率為0.01，某次仿真中，圖1（a）和（b）分別給出了在系統處于混沌臨界狀態時（取γd=0.8258）輸入白噪聲和高斯色噪聲時系統對應的時域圖和相軌跡圖，圖2（a）和（b）分別給出了在系統處于混沌臨界狀態時，輸入混有上述白噪聲的信號（信噪比為-23dB）和含有上述高斯色噪聲的信號時（信噪比為-20dB）對應的系統時域圖和相軌跡圖。其中，高斯色噪聲是由高斯白噪聲通過帶通濾波器后得到的。

由圖1和圖2可見，在上述仿真中，臨界狀態下輸入一定信噪比的含噪信號將使系統的狀態發生變化，而輸入噪聲則不會引起系統狀態變化，從而可將與內置信號同頻率的微弱信號檢測出來。

3 不同信噪比下的檢測性能

理論上，含噪信號輸入到處于混沌臨界狀態的混沌系統中，系統應從混沌狀態迅速轉化為大尺度周期狀態，即系統對應的最大Lyapunov指數變為負數［11］。但仿真實驗中發現在不同精度的臨界閾值下輸入一定信噪比的含噪信號也可能不會引起系統的狀態變化，即系統對應的最大Lyapunov指數仍保持為正數。

以輸入噪聲為10-6，輸入信號的信噪比為-10dB 為 例 ，分 別 取 γd=0.82，0.825，0.8258，0.82582725，每個臨界閾值下進行100次仿真實驗，得到噪聲功率為10-6，信噪比為-10dB時，各仿真中系統對應的最大Lyapunov指數如圖3所示。

系統狀態的判斷可以利用最大Lyapunov指數的符號來判斷，最大Lyapunov指數大于0說明系統處于混沌態，最大Lyapunov指數小于0說明系統處于周期態，因此可定義在混沌臨界狀態下，輸入信號后的檢測率為

由圖3及式（3）可知，在噪聲功率為10-6，信噪比為-10dB時，混沌臨界值為0.82、0.825、0.8258、0.82582725時對應的混沌系統檢測率分別為0%、0%、100%、100%。可見，在不同臨界閾值下，混沌振子的檢測性能是不同的。表1～表8給出了白噪聲功率分別為10-1～10-8，系統處于臨界狀態（選取不同精度的臨界值）輸入不同信噪比的信號時，系統對應的檢測結果。

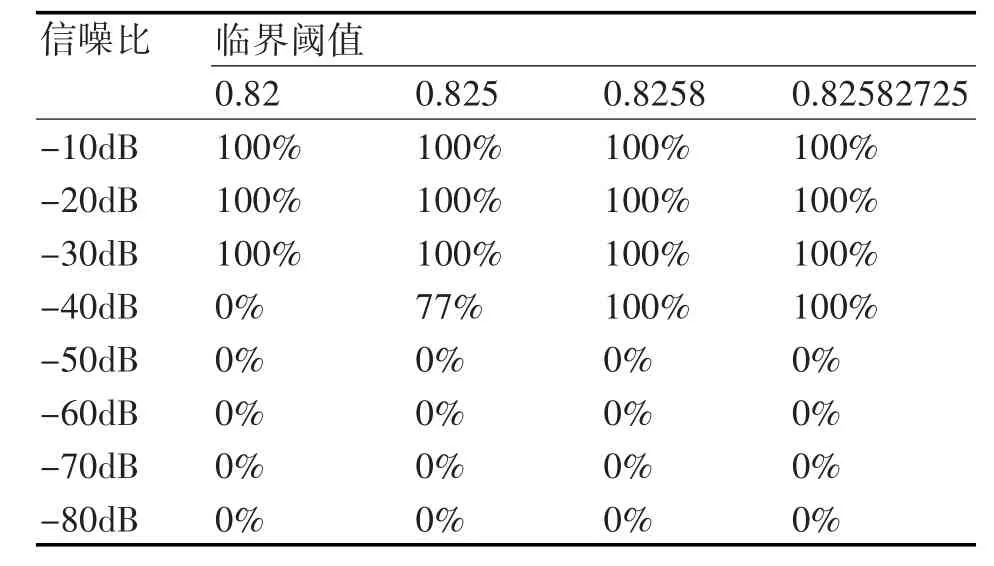
表1 白噪聲功率為10-1時，系統對應的檢測率

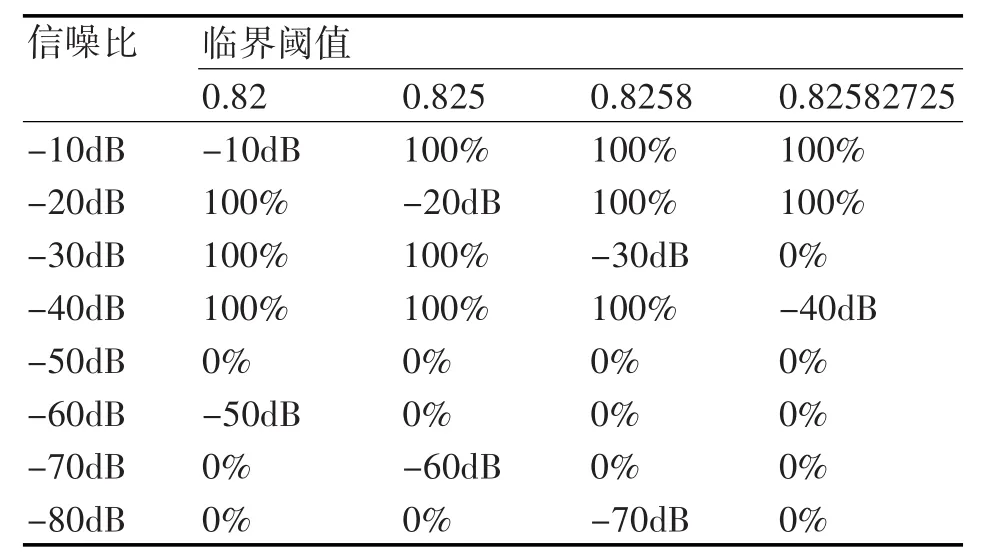
表2 白噪聲功率為10-2時，系統對應的檢測率

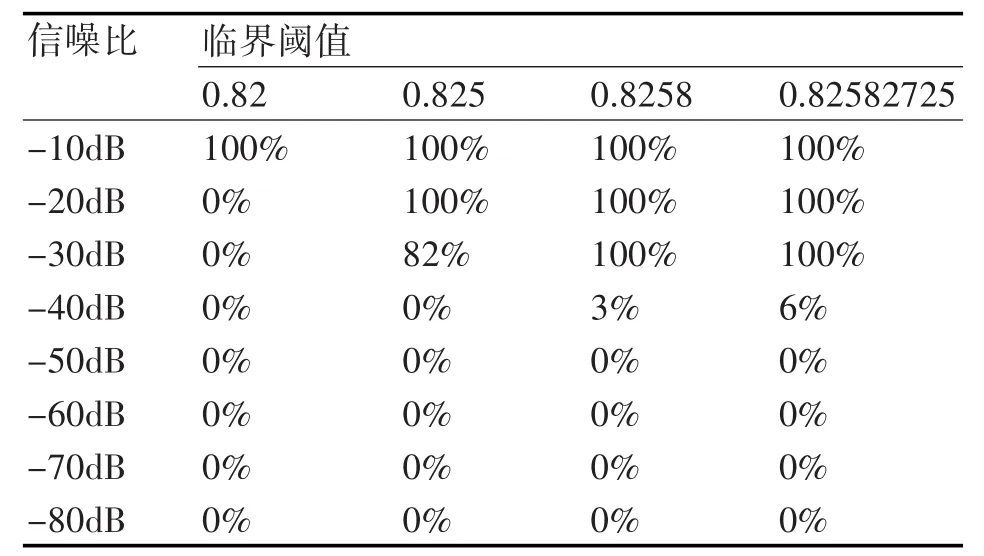
表3 白噪聲功率為10-3時，系統對應的檢測率

表4 白噪聲功率為10-4時，系統對應的檢測率

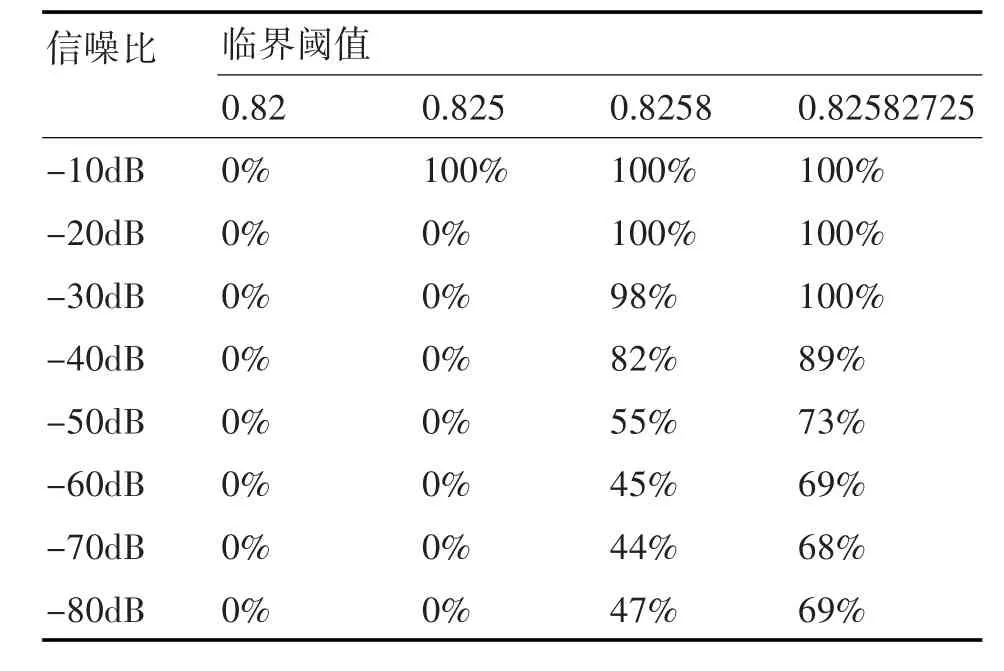
表5 白噪聲功率為10-5時，系統對應的檢測率

表6 白噪聲功率為10-6時，系統對應的檢測率

表7 白噪聲功率為10-7時，系統對應的檢測率

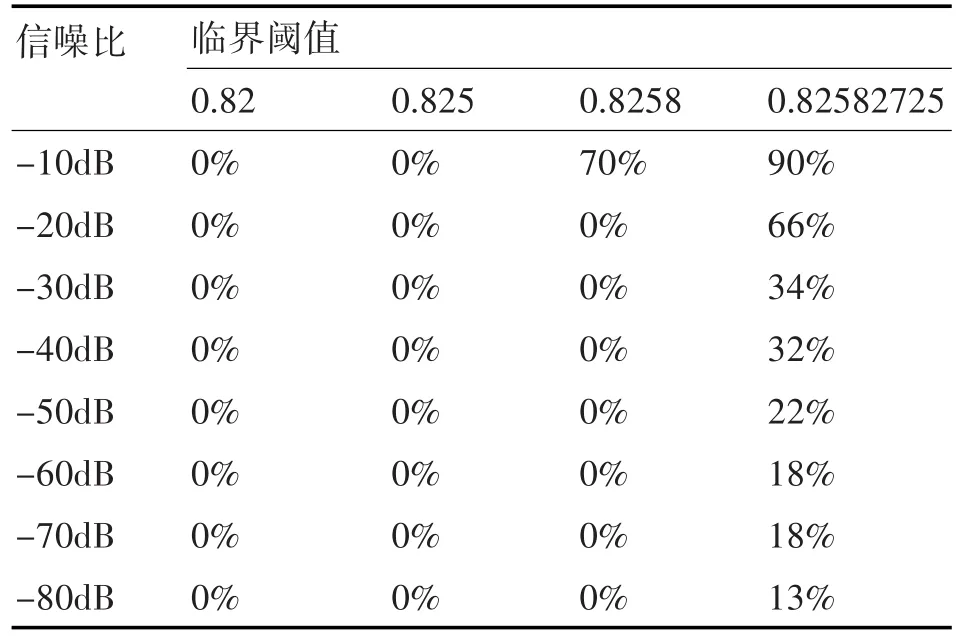
表8 白噪聲功率為10-8時，系統對應的檢測率

由表1～8可見，混沌系統的檢測性能與輸入背景噪聲功率及選取的臨界閾值都有關系。當背景噪聲很大時，需要較大的待測信號才能使系統從混沌狀態轉換到大尺度周期狀態。這主要是因為隨著系統噪聲的增大，系統的無序度將增大，系統要由無序度很高的混沌狀態轉變到大尺度周期狀態時，就需要增加系統中的有序度來克服這種無序度的影響，而系統的有序度體現在系統外加的周期策動力上。因此，當系統的噪聲較大時，系統轉變到大尺度周期狀態所需的周期策動力就要變大。在一定噪聲功率下，臨界閾值精度越高，能夠檢測到的信噪比越低，這主要是因為只有當選取的臨界閾值與信號幅度之和大于系統真實的臨界閾值時才能引起系統的相變，當選取的臨界閾值精度越高時越接近于真實的臨界閾值，較小的信號幅度即可引起系統的相變，因此選取較高精度的臨界閾值更能檢測到信噪比較低的信號，但以往的研究表明［12］，臨界閾值精度越高，越有可能引起系統的虛警，誤將噪聲也檢測為信號，因此選取合適的臨界閾值是至關重要的。

4 結語

本文通過計算混沌系統在臨界狀態下系統的最大Lyapunov指數小于0的次數與仿真總次數的比值來定義檢測率的概念，并利用檢測率來表征不同噪聲功率、不同精度臨界閾值下，混沌系統檢測不同信噪比信號的性能。檢測結果表明，混沌系統檢測不同信噪比信號的檢測性能與噪聲功率、選取的臨界閾值均有關系。對于混沌系統檢測而言，只有當待測信號的幅度與選取的臨界閾值之和大于真實的臨界閾值之后，才能引起系統的相變，從而將信號檢測出來，因此對于同一噪聲功率而言，臨界閾值精度越高，能檢測到的信噪比越低，但臨界閾值精度越高也越容易引起虛警，這是一對矛盾。

［1］聶春燕.混沌系統與弱信號檢測［M］.北京：清華大學出版社，2009，3：6-7，87.

［2］冀常鵬，郭偉平，姬紅紅.混沌振子微弱未知信號檢測方法的改進［J］. 噪聲與振動控制，2013，33（4）：207-211.

［3］陳軍.基于混沌理論的檢測系統應用研究綜述［J］.甘肅高師學報，2013，18（2）：21-25.

［4］張剛，胡韜，王穎.基于Melnikov函數Duffing系統微弱信號檢測［J］. 電子測量技術，2015，38（1）：109-112.

［5］Min ZHANG，Zhi-zhen LIU，Yan CAO，etal.Research and simulation on weak signal detection based on doffing oscillator and damping ratio perturbation［J］.Journal of Measurement Science and Instrumentation，2011，2（2）：161-163.

［6］朱斌.基于混沌理論的微弱信號檢測［J］.電子科技，2010，23（2）：65-67.

［7］朱來普，張陸勇，謝文風等.基于Duffing混沌振子的微弱信號檢測研究［J］. 無線電工程，2012，42（1）：17-20.

［8］李琳，劉春剛，石碩等.基于混沌和Lyapunov指數的微弱信號檢測方法［J］.黑龍江大學自然科學學報，2012，29（4）：556-560.

［9］冉莉，王民.一種強噪聲背景下微弱信號檢測方法研究［J］. 信息技術，2012，2：41-45.

［10］陳新國，王潔蕓.混沌振子在不同初值下檢測弱信號的性能分析［J］. 儀器儀表學報，2012，33（12）：2857-2862.

［11］張賓.Lyapunov特性指數的算法研究及其在弱信號混沌檢測中的應用［D］.長春：吉林大學，2004：5-6.

［12］石敏.噪聲對混沌系統檢測性能的影響［J］.艦船電子工程，2017，37（3）：118-121.