某水下航行體試驗實施過程質量隱患源熵求解?

余建平 劉偉才

（中國船舶重工集團公司七五〇試驗場質量技術基礎部 昆明 650051）

1 引言

隨著科學技術及生產力水平的迅猛發展，各種電子機械產品的科技含量也越來越高，軍工產品作為各類高端技術綜合體的產物，其工藝復雜程度所帶來的產品準備和試驗過程中導致質量問題發生的因素具有更多的綜合性、隨機性、復雜性。為此保證過程監督到位和加強事前預防的措施，提早規避或減少質量問題的發生就變得十分重要［1］。

本文運用“產品質量熵”理論提出了“試驗過程質量隱患源熵”概念，在收集了某水下航行體試驗及試驗準備全過程中質量問題的基礎上，從產品交接及方案策劃階段、裝配調試階段、實航實施階段、事后處理階段分析并整理了造成質量問題的關鍵因素，發現產品零件質量、參試/測試設備、人為（操作）、管理是導致質量問題發生的主要因素，給出了試驗過程質量隱患源熵的算法并進行了仿真求解，從而得到各隱患源的權重，并且通過仿真圖形對隱患源的重要度進行排序，為后續新產品質量問題的度量和預防提供了理論借鑒［2～4］。

2 試驗過程質量隱患源熵的概念

熵的概念起源于熱力學，后來由Shannon引入信息領域提出信息熵理論，并開創了熵在工程技術、經濟、社會應用的新紀元。熵就是描述一個系統的無序程度的變量。系統越亂，熵就越大，系統越有序，熵就越小。熵值法是突出局部差異的權重計算方法，是根據某同一指標觀測值之間的差異程度來反映其重要程度的［5］。

基于產品質量與信息熵在微觀概念思維方式上的相通之處，有關學者將熵引入質量管理領域來闡述產品不可控的質量損失，提出產品質量熵的概念。質量熵是質量損失的一種度量，從質量特性的角度，可用質量度對目標要求能力進行量化，即指質量完成或達到顧客滿意度的狀態概率［6］。從熵的角度來分析，它必然有一個與質量度相對應的質量熵來表示該質量特性的不確定度和無序度。當質量度越大時，其本身的不確定度和無序度就越小；反之，就越大。用質量度來定義其產品質量熵為：

其中，N為產品質量特性的個數、K為比例常數，同樣定義為K=1/ln N、Pi為第i個的狀態概率（質量度）。

基于“產品質量熵”理論，本文提出了“試驗過程質量隱患源熵”概念［7］。試驗過程質量隱患源熵存在于產品的各個階段（產品交接及方案策劃階段、裝配調試階段、實航實施階段、事后處理階段），是對影響靶場試驗過程質量潛在隱患的可能性度量。它綜合反映了靶場試驗全過程存在的一系列隱患問題對產品質量影響度的大小，某種試驗過程質量隱患源熵越大，則試驗過程質量影響度越大，從而輸出的產品在試驗全過程中的質量不確定性、無序度就越大，試驗過程發生質量問題的可能性就越大。試驗過程質量隱患源熵是試驗過程質量影響度的具體表現形式，其量化結果可作為對影響試驗過程權重較大的因素采取合理控制的標準［8～9］。

3 試驗過程質量隱患源熵的數學模型及算法

試驗過程質量隱患源熵的算法如下：1）分析產品從入場到事后處理過程導致質量問題的隱患源；2）將隱患源的原始數據進行標準化處理，得到矩陣R；3）計算各隱患源的每個指標對于影響度所有判斷指標的相對比重；4）計算各隱患源值；5）計算各隱患源熵權；6）計算各試驗過程質量隱患源熵綜合權重。

3.1 試驗過程質量隱患源熵的數學模型

試驗過程質量隱患源熵的數學模型首先應分析影響試驗質量的因素即試驗過程質量隱患源熵，假設 X={F1，F2，…，Fn}表示有n個主要隱患源集，用 Yi={Fi1，Fi2，…，Fim}表示第i個隱患源集，yij表示第i個隱患源的第j個屬性值，如果用目標函數值表示屬性，則為

這樣用n個隱患源的m個目標函數值表示的屬性則可構成隱患源的判斷矩陣為

由于不同隱患源數據具有不同的度量標準和方法，而且在數值上也可能有一定差異，因此為消除隱患源存在屬性和數量級的差異，需要對原始數據采用無量綱化的方法進行標準化處理。無量綱化的方法一般有收益型、成本型、固定型、區間型，本文采用成本型無量綱化方法對隱患源集進行標準化處理，具體模型為

當影響靶場試驗質量的隱患源在指標上的值完全相同時，熵值達到最大值1，熵權為0，表明該隱患源未提供任何有用信息，該隱患源可以不予考慮。當隱患源在指標上的值相差較大、熵值較小、熵權較大時，說明該隱患源是權重比較大的因素，應重點預防。各隱患源的每個指標對于該隱患源所有判斷指標的相對比重為

其中：κ=1/ln m。

熵權的本質是對數據信息有用程度的度量。如果某個影響因素的熵越小，說明其值的增減程度越大，提供的有用信息量越多越有利于作出正常與異常的判斷和選擇，在判斷該隱患源所起的作用就越大，即當該隱患源異常時，對試驗過程質量的影響越大，該隱患源的熵權越大［10～12］。因此，可得第 i個影響因數的熵權為

對于靶場試驗質量隱患源，使用專家法給出其主觀權重為 λi（i=1，2，…，n）。主觀權重是根據不同的行業、不同過程而確定的。因此，主觀權重對于試驗過程質量隱患源熵的確定具有實際意義。

在試驗過程質量隱患源熵權與主觀權重的基礎上，可得第i項隱患源的綜合權重為

其中：i=1，2，…n。

3.2 算法實現

利用Matlab對試驗過程質量隱患源熵權重的仿真步驟如下。

1）初始化參數，分析產品從入場到事后處理過程導致試驗質量問題的隱患源，將隱患源點F1，F2，…，Fn按順序排列，將每一個隱患源點分布在m個判斷指標下，獲得一個判斷矩陣R′。

2）根據具體情況利用成本型指標將初始判斷矩陣R′進行標準化處理，得到矩陣R。

3）計算各隱患源n個指標中的每個指標j對于隱患源所有判斷指標的相對比重 fij。

4）計算n類隱患源中第i個隱患源的熵值Hi，并計算第i個隱患源的熵權wi。

5）將熵權wi與專家法給出的權重 λi相結合計算第i項隱患源的綜合權重wi，算法結束。

4 應用仿真

4.1 靶場試驗過程質量隱患源熵組成模型

某水下航行體產品的質量控制不僅是產品研制過程的設計、材質、技術、生產等過程的質量控制，在靶場試驗時，產品準備的質量控制也是決定靶場試驗成敗的重要因素之一。在某水下航行體湖試全過程中，應以合格零件進行裝配調試為前提，即在裝配調試之前需保證產品硬件質量。在產品試驗實施之前，首先需要針對各分段和總體采用不同的裝配調試方法和設備進行裝配調試，同樣在產品試驗實施過程中，也要選擇相應的發控、參試/測試設備。在靶場試驗時，產品準備的質量控制還與組織管理和人為因素有關。根據上述分析，可建立產品靶場試驗全過程質量影響因數組成模型。

4.2 靶場試驗過程質量隱患源熵的仿真計算

圖1為靶場試驗過程質量隱患源組成模型，影響靶場試驗過程質量的主要隱患源可分為四類，每一個隱患源都有不同的量化標準，隱患源的權重也不同，在計算試驗過程質量隱患源熵的過程中，應具體分析，某水下航行體各類隱患源不同階段質量問題原始數據如表1所示。

表1 某水下航行體質量問題原始數據

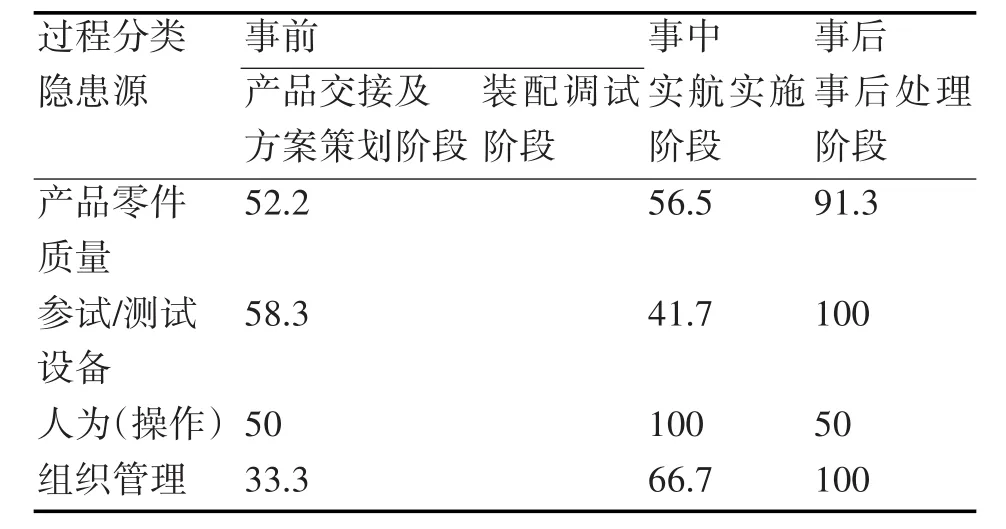
表2 各類隱患源不同階段下無質量問題百分率

表2中，數據是全年該型號產品各類隱患源不同階段質量問題統計（如表1所示），根據所得，數值越大表明該隱患源在此階段下狀態越穩定，反之則越不穩定；根據仿真算法步驟可得到如下結果：

由算法步驟1）可得模糊關聯矩陣為

由步驟3）可得各隱患數據每兩月與其它月份相對比重矩陣為

由步驟4）和5）可得靶場試驗過程質量隱患源熵權為

由于靶場試驗質量影響因數的主觀權重沒有通過專家判斷，不能給出靶場試驗質量隱患源合理的重要程度參考值，所以在此假設各質量隱患源主觀權重λ均為1。

由步驟5）可得靶場試驗過程質量隱患源熵的綜合權重為

根據上述計算過程，可將各類隱患源的綜合權重仿真如圖2所示。

圖2 中可以看出，通過對各類影響靶場試驗質量隱患源綜合權重的計算，可以很明確地得出各類靶場試驗過程質量隱患源的綜合權重。由仿真圖可得各類隱患源隱患度的權重排序為W：｛W4＞W2＞W1＞W3｝由此得出，在靶場試驗中，按2/8原則需重點控制的隱患源為W2和W4，即參試/測試設備與組織管理。由于本文質量隱患源主觀權重為假設值，所以最終數據結論不反映實際情況。

本文算法不僅得出綜合權重排序，并且還得出了各類隱患源隱患度的具體數值，因此可以對隱患源作針對性的控制與預防。

5 結語

本文在面向裝配調試過程質量熵的基礎上提出過程質量熵的概念，利用綜合熵權的思想，在借鑒信息熵計算方法的基礎上，將過程質量這一復雜的問題進行定量化處理，通過仿真算法來求解過程質量綜合權重，從而對各類過程質量關鍵程度進行排序，為主動預防提供了新的思路。

［1］侯惠芳，季新生，劉光強.異構無線網絡中基于標識的匿名認證協議［J］.通信學報，2011，32（5）：153-161.

［2］周彥偉，楊波，張文政.可證安全的移動互聯網可信匿名漫游協議［J］.計算機學報，2015，38（4）：733-748.

［3］王波，耿如軍.機械產品裝配調試過程質量熵研究［J］.制造業自動化，2009，31（9）：18-23.

［4］葛紅玉，張根保.機械產品裝配質量缺陷源熵的算法及求解分析［J］.計算機運用與研究，2010，27（10）：3807-3809.

［5］吳紅梅，金鴻章.基于熵理論復雜系統的脆性［J］.中南大學學報，2009，40（9）：347-351.

［6］丁正平，汪克夷.基于熵的直運型供應鏈庫存協調研究［J］.計算機集成制造系統，2008，14（5）：933-936.

［7］羅良靜，王靜.熵權法在企業統計質量控制中的應用［J］.統計與信息論壇，2004，19（6）：5-7.

［8］劉煜，鄭恒.基于熵的新產品開發決策方法［J］.科技進步與對策，2007，24（2）：155-156.

［9］王彬.基于知識的機械產品概念設計過程防錯理論與方法研究［D］.北京：北京航空航天大學，2008.

［10］王旭，葛顯龍，林云.供應商選擇的雙層規劃模型及求解分析［J］.計算機工程與應用，2009，45（23）：11-14.

［11］胡俊，胡賢德，程家興.基于Spark的大數據混合計算模型［J］.計算機系統應用，2015，24（4）：214-218.

［12］李鋒剛，魏炎炎，楊龍.基于和聲算法異構Hadoop集群資源分配優化［J］.計算機工程與應用，2014，50（9）：98-102.