等比法求和式極限
2018-03-22 08:12:44郭偉
長治學院學報 2018年5期
關鍵詞:定義
郭 偉
(長治學院 數學系,山西 長治 046011)
1 預備知識
在高等數學中,經常會遇到一些計算和式極限[1]的題型。由于極限的四則運算對和式極限是不成立的,我們可以將和式放大與縮小并借助于夾逼準則求一些特殊的和式極限,但很多情況下夾逼準則是不成立的。定積分的引入對計算和式極限提供了一個較好的方法[2]。眾所周知,定義在[a,b]上的定積分
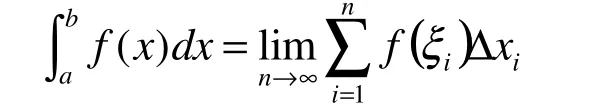

在函數可積的條件下,通常采取等分法和特殊取點法來計算定積分,例如將[0,1]區間n等分,并取ξi為區間的右端點,則

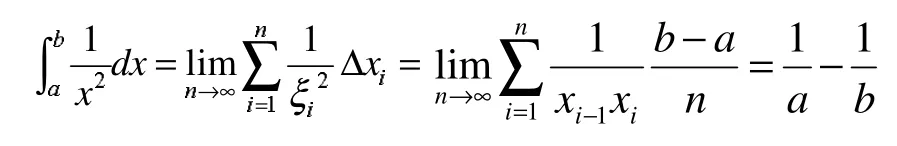
反過來,和式極限可以借助于定積分來計算,從上述兩個例子可以看出,等式最右端是一和式極限。這類極限有個基本的特征,是將區間等分來計算,即例子中的可以提取到求和符號之外,教材上主要介紹將這類和式極限轉化成定積分計算。例如:
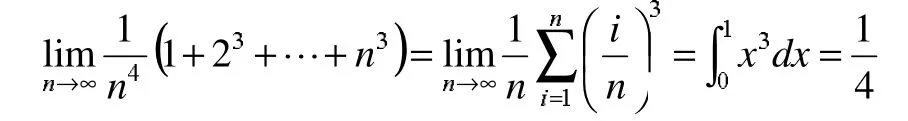
2 等比法計算和式極限
2.1 基本思想
設f(x)是定義在[1,b]上的連續函數,在[1,b]上插入n-1個特殊分點,依次為
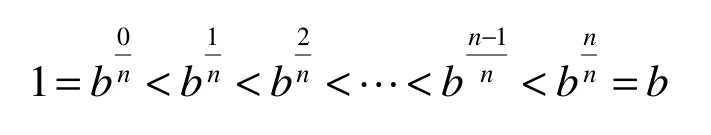
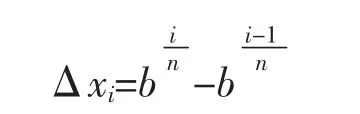
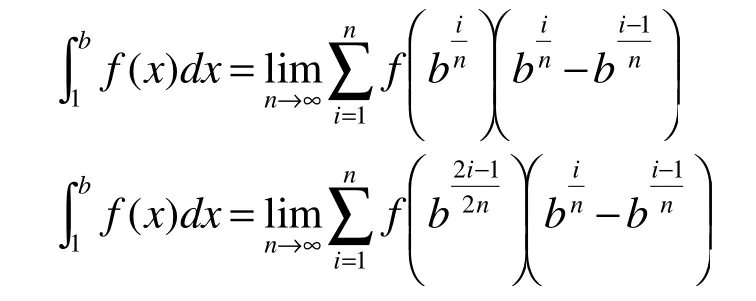
2.2 應用舉例
解:這是一個和式極限的問題,借助于定積分的定義可得:

2.2.2 計算
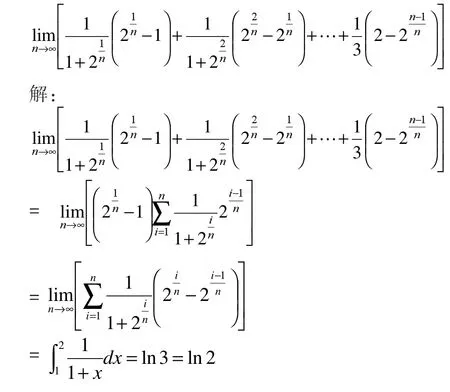
2.2.3 計算

小結
在計算和式極限時,我們首先將和式極限化為最簡單形式,從表達式觀察分割和取點的情況,然后轉化為定積分來計算,但如果是任意分割區間,取點不取端點和比例中項(例如取中點等),定積分則化為更復雜的和式極限。
猜你喜歡
幼兒教育·父母孩子版(2022年4期)2022-05-08 21:35:35
中學生數理化(高中版.高考數學)(2021年3期)2021-06-09 06:09:14
中學生數理化(高中版.高二數學)(2021年12期)2021-04-26 07:43:38
中學生數理化(高中版.高二數學)(2021年2期)2021-03-19 08:54:04
海峽姐妹(2020年9期)2021-01-04 01:35:44
華人時刊(2020年13期)2020-09-25 08:21:32
VOGUE服飾與美容(2020年9期)2020-09-02 14:47:26
山東青年(2016年1期)2016-02-28 14:25:25
汽車維護與修理(2015年6期)2015-02-28 12:16:55
當代修辭學(2014年3期)2014-01-21 02:30:44

