一種恒溫晶振老化趨勢擬合算法

韓文博

（中國電子科技集團公司第54研究所，河北石家莊，050081）

0 引言

在恒溫晶振的使用過程當中，其頻率準確度是保持整個系統(tǒng)時鐘鎖定的關(guān)鍵指標。頻率的實時準確度是由恒溫晶振的日老化、日波動、溫度漂移、電源漂移等因素共同累積的結(jié)果，其中老化指標是影響恒溫晶振頻率準確度的一個重要指標。本文介紹了一種自動批量擬合恒溫晶振長期老化指標的方法，在批量生產(chǎn)中對產(chǎn)品質(zhì)量的判定起了關(guān)鍵性作用。

1 最小二乘法介紹

最小二乘法是一種通過尋找最小化誤差平方和來擬合最佳匹配函數(shù)的方法假設(shè)數(shù)據(jù)偏差的平方和為H，其表達式為：

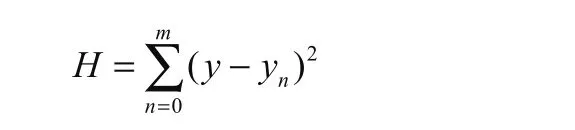
其原理可以解釋為：假設(shè)直線y=ax+b是這N個點最佳的匹配函數(shù)，這N個點偏離直線y ax b= + 是由于噪聲引起的，一個點偏離越遠是因為噪聲越大，其出現(xiàn)的概率越小，其偏離的程度與出現(xiàn)的概率符合正態(tài)分布，已知點集N，求直線y ax b= + 出現(xiàn)的概率就可以表示為： (|)P y N ，根據(jù)貝葉斯定理：

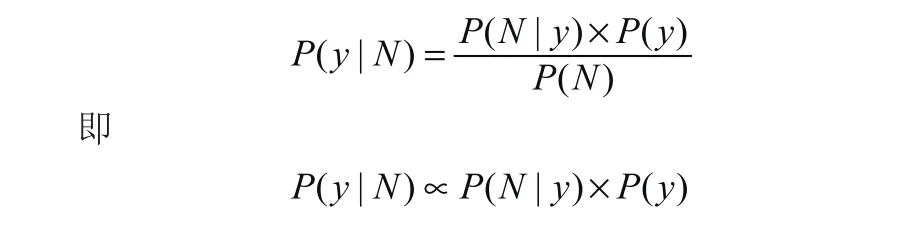
問題變?yōu)橛芍本€y ax b= + 生成點集N，假設(shè)點集N中每一個點都是獨立的那么：

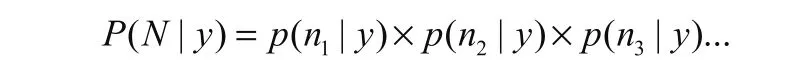
結(jié)合正態(tài)分布：

2 單純形法與二分查找介紹

單純形法是一種迭代算法，其基本原理為：先設(shè)定一個基可行解，根據(jù)最優(yōu)理論判斷此解是否為最優(yōu)解，是則輸出結(jié)果，計算停止；否則按規(guī)則重新定義基可行解，重新判斷，迭代循環(huán)，當找到最優(yōu)解后終止。

二分查找算法也稱折半查找算法，是一種常用的查找算法。二分查找算法是建立在有序數(shù)組基礎(chǔ)上的，從數(shù)組的中間值開始，如果中間值正好是目標值，則查找過程結(jié)束；如果待查值大于或小于中間值，則在大于或小于中間值的那一半中查找，在這一半中再次取中間值進行查找，直到找到目標值或者超出設(shè)定范圍后終止。

3 恒溫晶振老化系數(shù)擬合算法

晶體振蕩器長期老化模型公式：

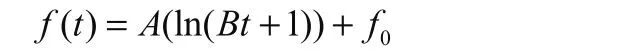
f( t)：晶體振蕩器的頻率

t：老化開始頻率穩(wěn)定后開始計時的天數(shù)

A、B、f0：需要擬合確定的常數(shù)

首先，進行B值擬合，設(shè)定B取值的范圍B1~B2，然后根據(jù)二分查找算法在這個范圍內(nèi)取中值Bm。

B值擬合函數(shù)u(t)：

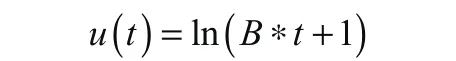
實測數(shù)據(jù)得到函數(shù)y(t)：

根據(jù)擬合函數(shù)u(t)與實測函數(shù)y(t)計算A與C（晶體振蕩器長期老化模型公式中的f0）

計算公式為：

確定新更優(yōu)基可行解的方法為在中值Bm前后取兩個值Bma與Bmb，代入晶振的長期老化模型：f ( t)= A( ln( B t+1))+f0，使用最小二乘法算出數(shù)據(jù)偏差的平方和：

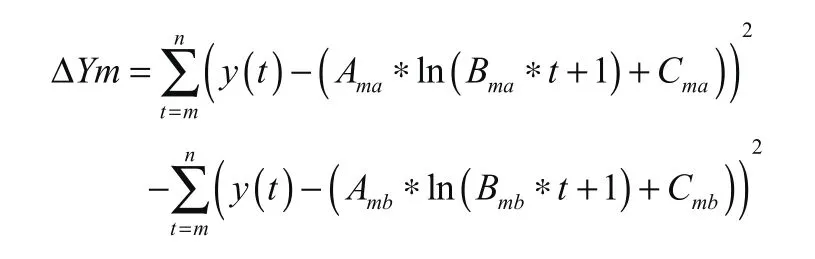
使用二分查找算法：

若Δym=0，則B值合適。

若Δym＜0，說明Bma比Bmb更接近實際曲線，B值應(yīng)取在B1～Bm這一區(qū)間，繼續(xù)迭代計算。

若ΔYm＞0，說明Bmb比Bma更接近實際曲線，B值應(yīng)取在Bm～B2這一區(qū)間，繼續(xù)迭代計算。

最終若|Bma-Bmb|＜B1，認為此時B值適。

擬合數(shù)據(jù)與實測數(shù)據(jù)的差值由殘差δ來衡量，表示了擬合值與實際值的一致性，計算公式為：

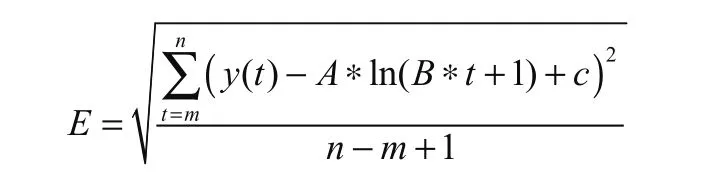
在生產(chǎn)過程當中由EXCEL根據(jù)測試數(shù)據(jù)利用VBA功能自動完成以上算法，并得出判定結(jié)論。

4 數(shù)據(jù)驗證

根據(jù)生產(chǎn)測試數(shù)據(jù)，截取前30天數(shù)據(jù)擬合長期數(shù)據(jù)，與實際長期測試數(shù)據(jù)對比。

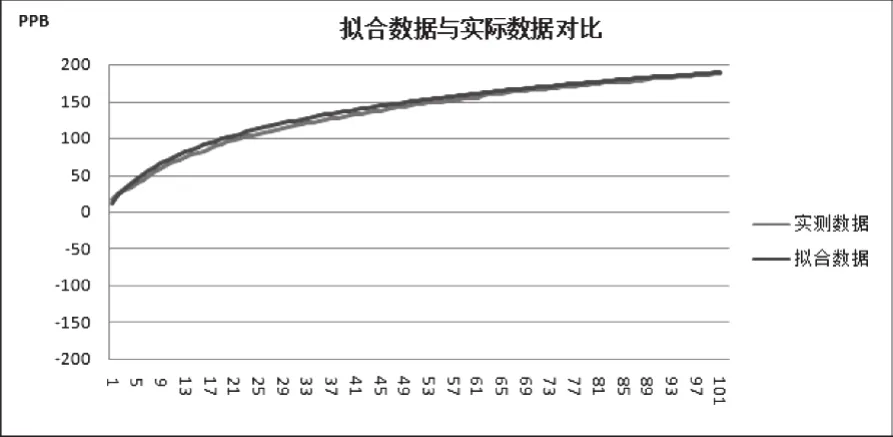
圖1 測試數(shù)據(jù)

實際生產(chǎn)中的大量數(shù)據(jù)證明，擬合數(shù)據(jù)與實際數(shù)據(jù)基本吻合，此方法可以作為長期老化判定的依據(jù)。

5 結(jié)束語

本文通過使用單純形法結(jié)合二分查找與最小二乘法進行迭代逼近求解恒溫晶振長期老化模型的系數(shù)，擬合計算恒溫晶振長期老化指標，利用VBA實現(xiàn)批量數(shù)據(jù)的自動計算與判定。此方法可較好地描述恒溫晶振長期老化過程，對恒溫晶振老化過程能做出有效的預測。本方法已經(jīng)應(yīng)用于生產(chǎn)實際，為產(chǎn)品質(zhì)量的判定提供了依據(jù)。

[1] 薛沖.基于晶體振蕩器的老化建模及其智能補償[D].西安電子科技大學,2014.

[2] 張威威.晶振老化漂移的建模與補償[D].西安電子科技大學,2012.

[3] 岳雪嬌,劉瑛.VB中實現(xiàn)最小二乘法數(shù)據(jù)處理[J].機械設(shè)計與制造 , 2016(10)： 159-162.