模型有差異 類比需謹慎

宋輝武 劉 博

(1. 鄂爾多斯市第一中學，內蒙古 鄂爾多斯 017010； 2. 長春師范大學物理學院，吉林 長春 130032)

筆者閱讀了本刊2017年第6期一篇論文《2015年高考全國卷Ⅱ第21題評講有感》,[1]對該文提出的模型遷移很感興趣,該文將光滑半圓形軌道上質點運動的模型與高考題中的桿連物系的質心運動的模型進行類比,并以此來解釋說明桿何時由頂變拉．經過深入思考仔細計算后,筆者發現文中的兩個核心觀點有失偏頗,實際上文中提到的兩種模型形似而神異,作者只關注形式上的相似而忽視神韻上的差異,因此得出了一些經不住推敲的錯誤結論．

圖1 圖2

1 圖2中質心的運動情況和圖1中的質點的運動情況并不相同

首先我們設圖1中的質點的質量為2m,圖2中的a、b球的質量皆為m,桿長為2l,則我們根據動能定理，對于圖1可得

(1)

對于圖2可得

(2)

因質心位于桿的中點,因此質心的水平分速度與豎直分速度正好是a、b球的速度的一半(當然質心的水平分加速度與豎直分加速度也是a、b球的加速度的一半),即

(3)

(4)

因此(2)式可改寫成

(5)

(6)

可以看出(6)式與(2)式是相同的，重力所做的功并不等于質心動能而是等于質心動能加相對動能(此即為柯尼希定理的內容)．而圖1的模型中重力所做的功全都轉化為質點的動能,由此可以看出當圖1中的質點與圖2中的質心處于相同位置時,二者的速度并不相等,質心的速度必小于質點的速度,也就是說圖2中質心的運動情況和圖1中的質點的運動情況并不相同．

2 光滑豎直桿對b的彈力與光滑水平面對a的彈力的合力并不是背離圓心或指向圓心

根據質心運動定理可得

(7)

(8)

找到aa和ab的關系也就能夠確定Na和Nb的關系,下面我們再來尋找aa和ab的關系.

設Oa長度為x,則x=2lcosθ,兩邊同時對時間求導得

(9)

又vacosθ=vbsinθ,

(10)

則

(11)

將(9)式代入(11)式解得

(12)

(13)

將(7)、(8)兩式代入(13)式可得

整理后為

g-ab=aatanθ,

(14)

根據(2)式可得

(15)

將(15)式對時間求導后可得

aa=gcosθ(3sinθ-2),

(16)

由(12)、(14)、(15)式可得

aa=gcosθ(3sinθ-2).

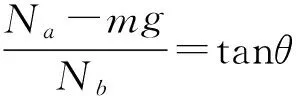
(1) 開始一段時間桿是頂的狀態,此時滿足Na-mg>0,且Nb>0,物理意義為Na>mg,且Nb方向為水平向右,這個過程中Na-mg與Nb的合力方向是背離圓心的.

(2) 后一段時間桿是拉的狀態,此時滿足Na-mg<0,且Nb<0,物理意義為Na

(3) 臨界情況即為桿上的彈力為0,此時桿既不頂也不拉,且滿足Na=mg,Nb=0．

Na-mg與Nb的合力的變化趨勢為:方向先是背離圓心,大小逐漸減小為0,然后方向變為指向圓心,大小由0逐漸增大．Na-mg和Nb的變化趨勢同樣為逐漸減小到0再反向逐漸增大,即與合力的變化趨勢保持一致．

1 唐召軍.2015年高考全國卷Ⅱ第21題評講有感[J].物理教師,2017(6):92-93.